Задачи на движение. Задание 23

1.

2.

Два велосипедиста одновременно отправляются в 140-километровый
пробег. Первый едет со скоростью, на 6 км/ч большей, чем второй, и
прибывает к финишу на 3 часа раньше второго. Найдите скорость
велосипедиста, пришедшего к финишу вторым.

3.

Два велосипедиста одновременно отправляются в 140-километровый
пробег. Первый едет со скоростью, на 6 км/ч большей, чем второй, и
прибывает к финишу на 3 часа раньше второго. Найдите скорость
велосипедиста, пришедшего к финишу вторым.
( х 6)км / ч
Решение:
хкм / ч
140км

4.

Решение:
Пусть х км/ч − скорость велосипедиста, пришедшего
к финишу вторым, тогда ( х + 6) км/ч − скорость
велосипедиста, пришедшего к финишу первым.
х>0
v (км/ч)
t (ч)
s (км)
1 велосипедист
х+6
140
х 6
140
2 велосипедист
х
140
х
140

5.

Решение:
140 140
3 х( х 6)
х
х 6

6.

Решение:
140 140
3 х( х 6)
х
х 6
140( х 6) 140 х 3 х( х 6)

7.

Решение:
140 140
3 х( х 6)
х
х 6
140( х 6) 140 х 3 х( х 6)
140 х 840 140 х 3х 2 18 х

8.

Решение:
140 140
3 х( х 6)
х
х 6
140( х 6) 140 х 3 х( х 6)
140 х 840 140 х 3х 2 18 х
840 3 х 2 18 х
3х 2 18 х 840 0 : 3
х 2 6 х 280 0

9.

Решение:
а 1
140 140
3 х( х 6)
х
х 6
140( х 6) 140 х 3 х( х 6)
b 6
140 х 840 140 х 3 х 2 18 х
D b 2 4ac 36 4 1 ( 280) 36 1120 1156
840 3х 2 18 х
3х 2 18 х 840 0 : 3
х 2 6 х 280 0
c 280

10.

Решение:
а 1
140 140
3 х( х 6)
х
х 6
140( х 6) 140 х 3 х( х 6)
b 6
140 х 840 140 х 3 х 2 18 х
D b 2 4ac 36 4 1 ( 280) 36 1120 1156
c 280
840 3х 2 18 х
3х 18 х 840 0 : 3
2
х 2 6 х 280 0
х1
b D 6 34 28
14( км / ч)
2а
2 1
2
х1
b D 6 34 40
20 ОДЗ
2а
2 1
2
Ответ: 14 км/ч.

11.

Из двух городов одновременно навстречу друг другу отправились
два велосипедиста. Проехав некоторую часть пути, первый
велосипедист сделал остановку на 36 минут, а затем продолжил
движение до встречи со вторым велосипедистом. Расстояние между
городами составляет 120 км, скорость первого велосипедиста равна
10 км/ч, скорость второго − 20 км/ч. Определите расстояние от
города, из которого выехал второй велосипедист, до места встречи.

12.

Из двух городов одновременно навстречу друг другу отправились
два велосипедиста. Проехав некоторую часть пути, первый
велосипедист сделал остановку на 36 минут, а затем продолжил
движение до встречи со вторым велосипедистом. Расстояние между
городами составляет 120 км, скорость первого велосипедиста равна
10 км/ч, скорость второго − 20 км/ч. Определите расстояние от
города, из которого выехал второй велосипедист, до места встречи.
120 х км
10км / ч
х км
20км / ч

13.

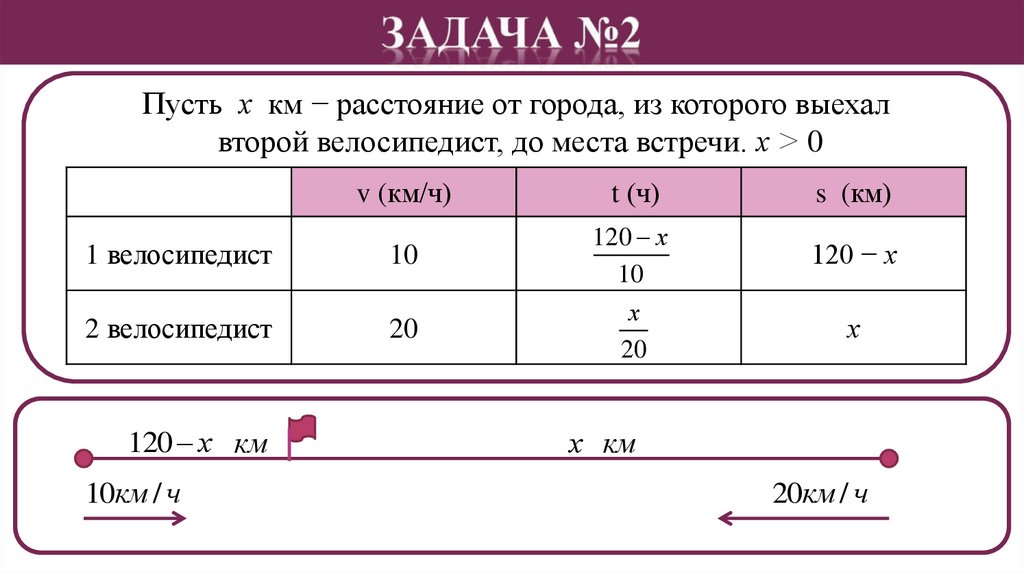
Пусть х км − расстояние от города, из которого выехал
второй велосипедист, до места встречи. х > 0
v (км/ч)
1 велосипедист
10
2 велосипедист
20
120 х км
10км / ч
t (ч)
120 х
10
х
20
s (км)
120 − х
х
х км
20км / ч

14.

Решение:
36 мин
36
3
ч ч
60
5
120 х 3 х
20
10
5 20
2 (120 х) 3 4 х
240 2 х 12 х

15.

Решение:
36 мин
36
3
ч ч
60
5
120 х 3 х
20
10
5 20
2 (120 х) 3 4 х
240 2 х 12 х
2 х х 240 12
3 х 252
х 252 : 3
х 84(км)
Ответ: 84 км.

16.

Свежие фрукты содержат 88% воды, а высушенные—30%.
Сколько сухих фруктов получится из 35 кг свежих фруктов?

17.

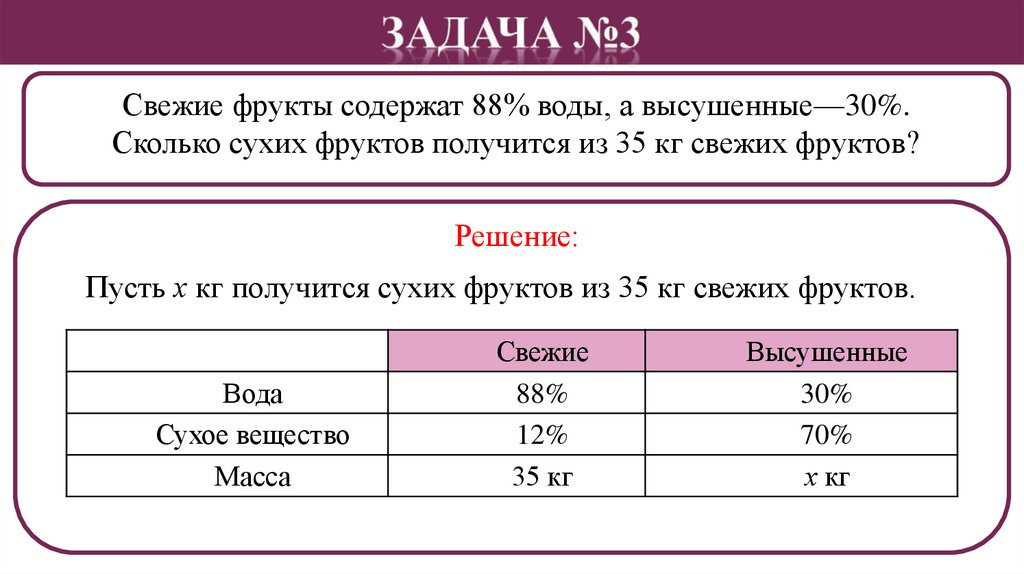
Свежие фрукты содержат 88% воды, а высушенные—30%.
Сколько сухих фруктов получится из 35 кг свежих фруктов?
Решение:
Пусть х кг получится сухих фруктов из 35 кг свежих фруктов.
Вода
Сухое вещество
Масса
Свежие
88%
12%
35 кг
Высушенные
30%
70%
х кг

18.

Свежие фрукты содержат 88% воды, а высушенные—30%.
Сколько сухих фруктов получится из 35 кг свежих фруктов?
Решение:
35 12 х 70
100
100
35 12 70х
70х 420
х 420 : 70
х 6( кг )
Ответ: 6 кг.

19.

Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты
различной концентрации. Если их смешать, то получится раствор,
содержащий 33% кислоты. Если же смешать равные массы этих
растворов, то полученный раствор будет содержать 47% кислоты.
Сколько килограммов кислоты содержится в первом сосуде?

20.

Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты
различной концентрации. Если их смешать, то получится раствор,
содержащий 33% кислоты. Если же смешать равные массы этих
растворов, то полученный раствор будет содержать 47% кислоты.
Сколько килограммов кислоты содержится в первом сосуде?
Решение:
40 х 20 у 60 33
Пусть х % − концентрация кислоты в первом сосуде,
100
100
100
у % − концентрация кислоты во втором сосуде.
1 х 1 у 2 47
100 100 100

21.

Решение:
40 х 20 у 60 33
100 100 100
1 х 1 у 2 47
100 100 100

22.

Решение:
40 х 20 у 60 33
100 100 100
1 х 1 у 2 47
100 100 100
40 х 20 у 60 33
100 100 100 100
1 х 1 у 2 47 100
100 100 100

23.

Решение:
40 х 20 у 60 33
100 100 100
1 х 1 у 2 47
100 100 100
40 х 20 у 60 33
100 100 100 100
1 х 1 у 2 47 100
100 100 100
40 х 20 у 1980
х у 94

24.

Решение:
40 х 20 у 1980
х у 94
40 х 20 у 1980
х у 94 20

25.

Решение:
40 х 20 у 1980
х у 94
40 х 20 у 1980
х у 94 20
40 х 20 у 1980
20 х 20 у 1880

26.

Решение:
40 х 20 у 1980
х у 94
40 х 20 у 1980
х у 94 20
40 х 20 у 1980
20 х 20 у 1880
20х 100
х 5% − концентрация кислоты
в первом сосуде

27.

Решение:
40 х 20 у 1980
х у 94
40 х 20 у 1980
х у 94 20
40 х 20 у 1980
20 х 20 у 1880
20х 100
х 5% − концентрация кислоты
в первом сосуде
40 5 200
2 (кг) − кислоты
100 100
в первом сосуде
Ответ: 2 кг.

28.

Поезд, двигаясь равномерно со скоростью 26 км/ч, проезжает
мимо пешехода, идущего параллельно путям со скоростью 4 км/ч
навстречу поезду, за 90 секунд. Найдите длину поезда в метрах.

29.

Поезд, двигаясь равномерно со скоростью 26 км/ч, проезжает
мимо пешехода, идущего параллельно путям со скоростью 4 км/ч
навстречу поезду, за 90 секунд. Найдите длину поезда в метрах.
Решение:
1) 26 + 4 = 30(км/ч) – скорость сближения

30.

Поезд, двигаясь равномерно со скоростью 26 км/ч, проезжает
мимо пешехода, идущего параллельно путям со скоростью 4 км/ч
навстречу поезду, за 90 секунд. Найдите длину поезда в метрах.
Решение:
1) 26 + 4 = 30(км/ч) – скорость сближения
2) 30 км / ч 30 000 м / ч
30000
м/с
3600

31.

Поезд, двигаясь равномерно со скоростью 26 км/ч, проезжает
мимо пешехода, идущего параллельно путям со скоростью 4 км/ч
навстречу поезду, за 90 секунд. Найдите длину поезда в метрах.
Решение:
1) 26 + 4 = 30(км/ч) – скорость сближения
2) 30 км / ч 30 000 м / ч
30000
300
100
25
м/с
м/с
м/с м/с
3600
36
12
3

32.

Поезд, двигаясь равномерно со скоростью 26 км/ч, проезжает
мимо пешехода, идущего параллельно путям со скоростью 4 км/ч
навстречу поезду, за 90 секунд. Найдите длину поезда в метрах.
Решение:
1) 26 + 4 = 30(км/ч) – скорость сближения
2) 30 км / ч 30 000 м / ч
3)
30000
300
100
25
м/с
м/с
м/с м/с
3600
36
12
3
25
м / с · 90 с 25 · 30 м 750 м
3
Ответ: 750 м.