Similar presentations:
Простейшие вероятностные задачи
1. МБОУ «Средняя школа №2 им.Е.В. Камышева» г.Гагарин Смоленской области
Учитель математикиНикитина Елена Анатольевна
Высшая кв. категория
2.
раздел математики,изучающий закономерности
случайных явлений:
случайные события
(далее СС), случайные
величины, их свойства и
операции над ними.
(Советский
энциклопедический словарь,
1982 год)
3. Основные понятия
Познание действительности в естественных науках происходит в результате испытаний(эксперимента, наблюдений, опыта).
Испытанием или опытом называется осуществление какого-нибудь определенного комплекса условий,
который может быть воспроизведено сколь угодно большое число раз.
Случайным (СС)называется событие, которое может произойти или не произойти в результате
некоторого испытания (опыта).
Таким образом, событие
рассматривается как результат
испытания.
Пример.
Бросание монеты – это испытание.
Появление орла при бросании –
событие.
4. Основные понятия
Наблюдаемые нами события различаются постепени возможности их появления и по характеру
их взаимосвязи.
Событие называется достоверным, если оно
обязательно произойдет в результате данного
испытания.
Пример. Получение студентом положительной
или отрицательной оценки на экзамене есть
событие достоверное, если экзамен протекает
согласно обычным правилам.
Событие называется невозможным, если оно не
может произойти в результате данного испытания.
Пример. Извлечение из урны белого шара, в
которой находятся лишь цветные (небелые) шары,
есть событие невозможное.
Два или несколько событий
называются равновозможными в данном испытании, если
имеются основания считать, что ни одно из этих событий не
является более возможным или менее возможным, чем
другие.
Пример. При одном бросании одной и той же игральной
кости появление 1, 2, 3, 4, 5 и 6 очков - все это события
равновозможные.
Два события называются несовместными в данном
испытании, если появление одного из них исключает
появление другого, и совместными в противном случае.
Пример. В ящике имеются стандартные и нестандартные
детали. Берем на удачу одну деталь. Появление стандартной
детали исключает появление нестандартной детали. Эти
события несовместные.
События А и В называются противоположными, если
всякое наступление события А означает ненаступление
события В.
Обозначение:
А -событие А
_
А - событие противоположное событию А
(читается «не A»).
Пример. Попадание и промах при одном выстреле по
цели - события противоположные.
5. ИТАК…
Случайное событие (СС)- это событие, которое либопроизойдёт, либо нет.
Каждое случайное событие (СС) иметь свою вероятность
произойти (сбыться, реализоваться).
Испытание – любое действие, которое может привести к
одному или нескольким результатам.
Исход - конечный результат испытания. Значит испытание
может иметь один или несколько исходов.
Благоприятный исход - желаемый исход.
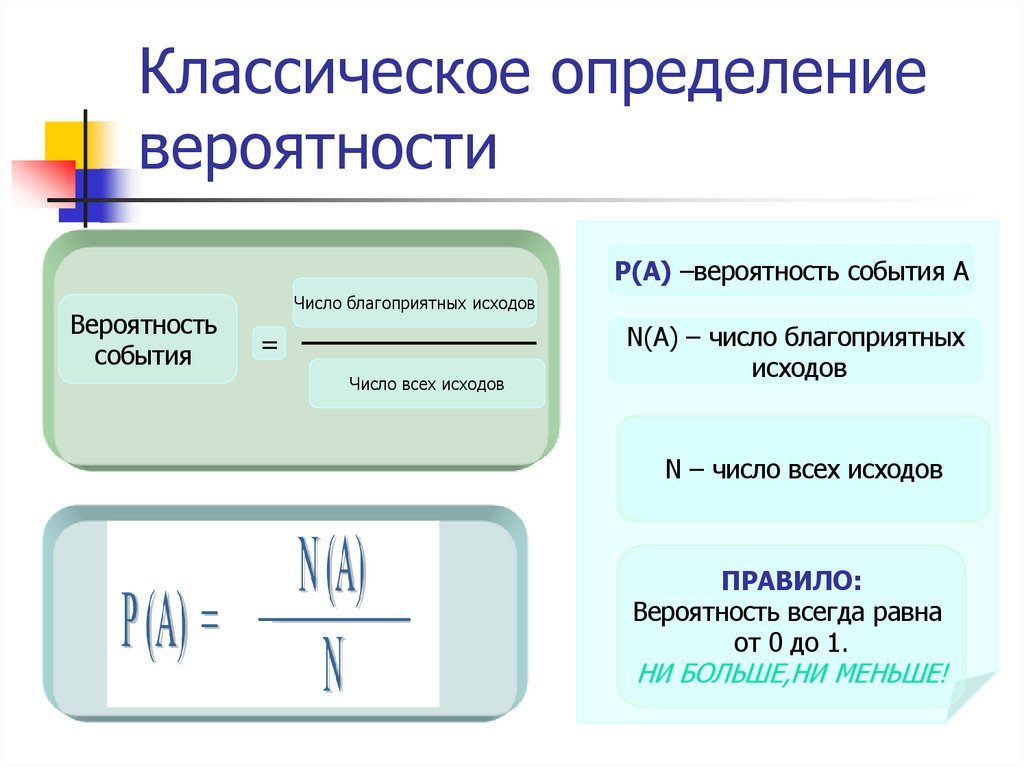
6. Классическое определение вероятности
Р(А) –вероятность события АВероятность
события
Число благоприятных исходов
=
Число всех исходов
N(A) – число благоприятных
исходов
N – число всех исходов
ПРАВИЛО:
Вероятность всегда равна
от 0 до 1.
НИ БОЛЬШЕ,НИ МЕНЬШЕ!
7. ЗАДАЧА №1.
Найти вероятность того, чтопри одном бросании
игральной кости (кубика)
выпадет:
а) три очка,
б) число очков, кратное трем,
в) число очков, большее трех,
г)число очков, не кратное трем.
8. Решение задачи №1(а): выпадет: а) три очка
9. Решение задачи №1(б): выпадет: б) число очков, кратное трем
10. Решение задачи №1(в): выпадет: в) число очков, большее трех
11. Решение задачи №1(а): выпадет: г) не кратное трем
12. Задача №2
Найти вероятность того, что при вытаскиванииодной карты из колоды( 52 карты) эта карта окажется:
а) дамой пик,
б) дамой любой масти,
в) картой пиковой масти,
г) картой черной масти.
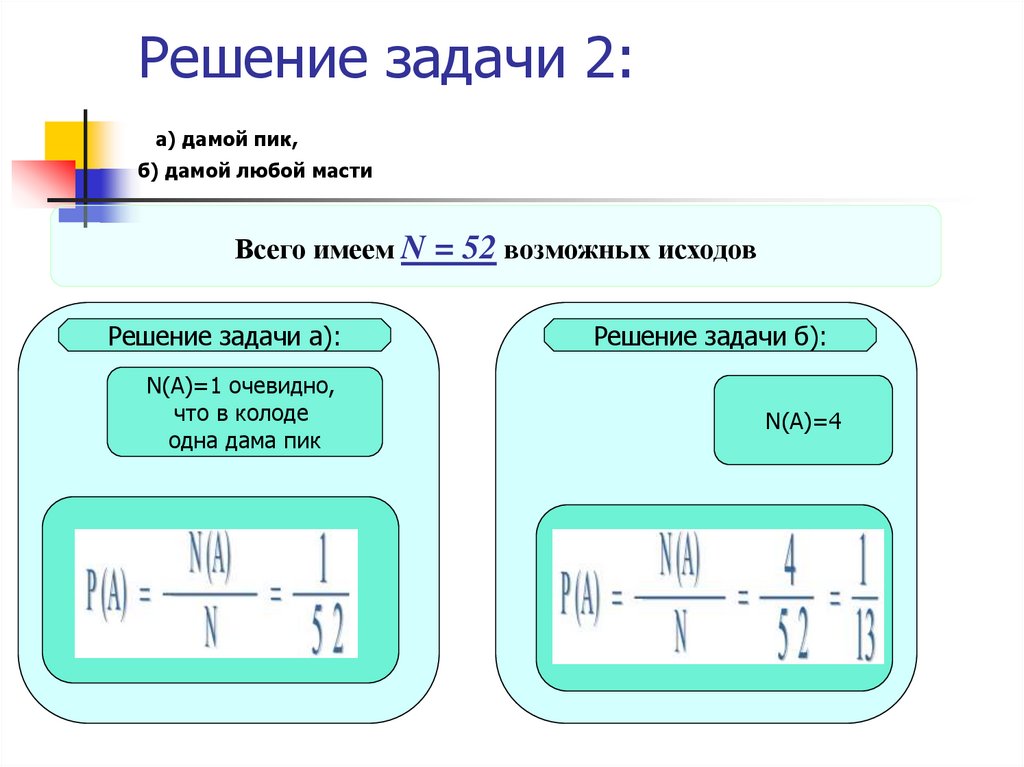
13. Решение задачи 2: а) дамой пик, б) дамой любой масти
Всего имеем N = 52 возможных исходовРешение задачи а):
Решение задачи б):
N(А)=1 очевидно,
что в колоде
одна дама пик
N(А)=4
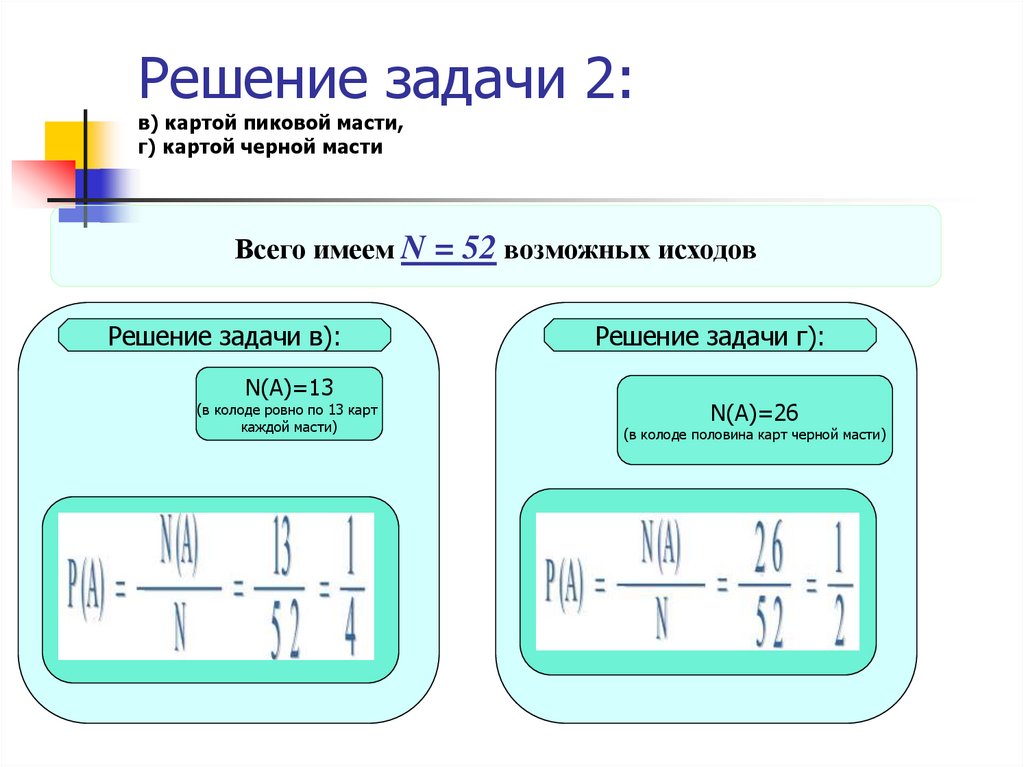
14. Решение задачи 2: в) картой пиковой масти, г) картой черной масти
Всего имеем N = 52 возможных исходовРешение задачи в):
N(А)=13
(в колоде ровно по 13 карт
каждой масти)
Решение задачи г):
N(А)=26
(в колоде половина карт черной масти)
15. Задача № 3
Найти вероятностьтого, что при
подбрасывании
двух костей
одновременно
суммарное число
очков будет равным
пяти.
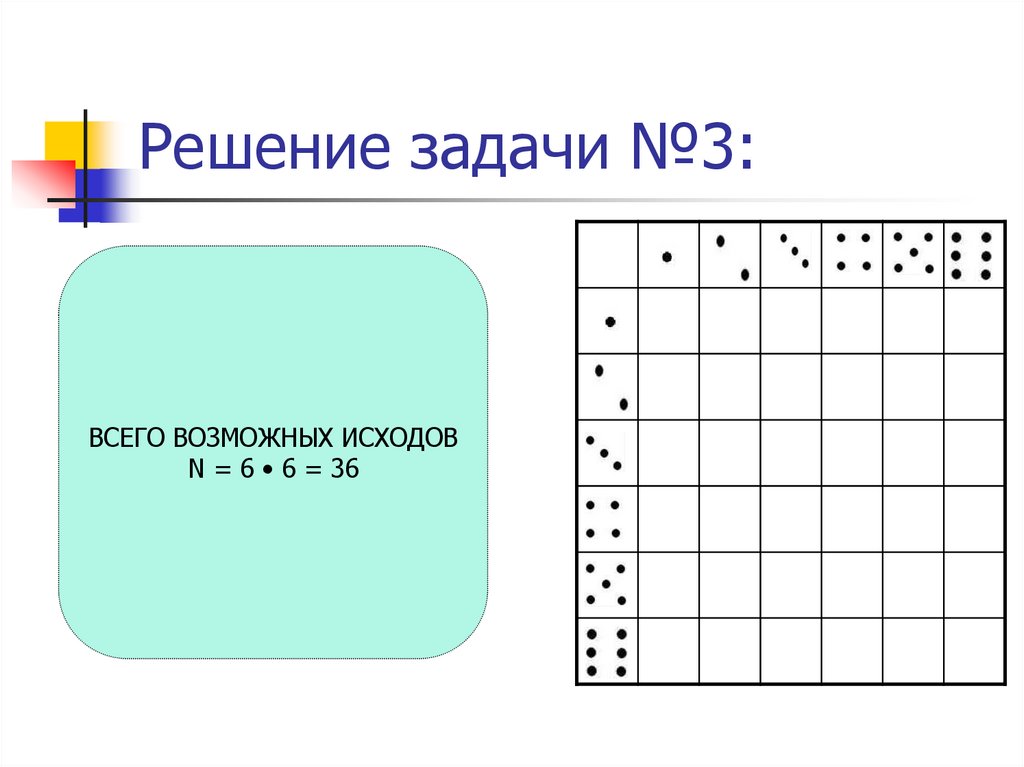
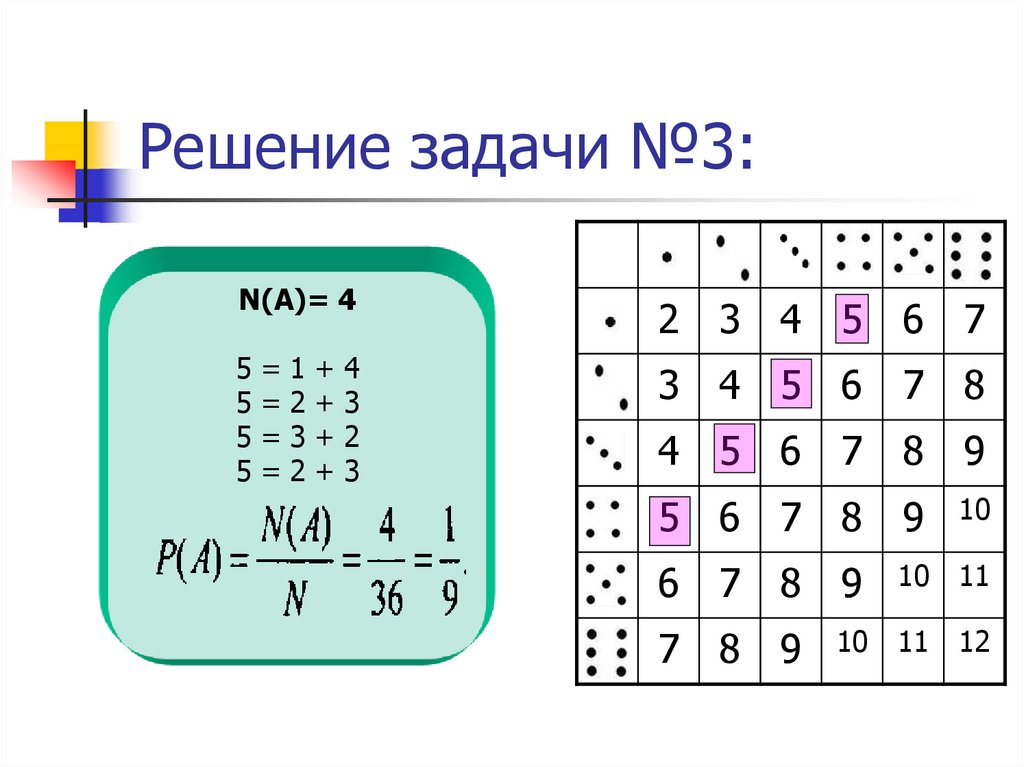
16. Решение задачи №3:
ВСЕГО ВОЗМОЖНЫХ ИСХОДОВN = 6 • 6 = 36
17. Решение задачи №3:
N(А)= 42 3 4 5 6 7
5=1+4
5=2+3
5=3+2
5=2+3
3 4 5 6 7 8
4 5 6 7 8 9
5 6 7 8 9
10
6 7 8 9
10
11
10
11
12
7 8 9
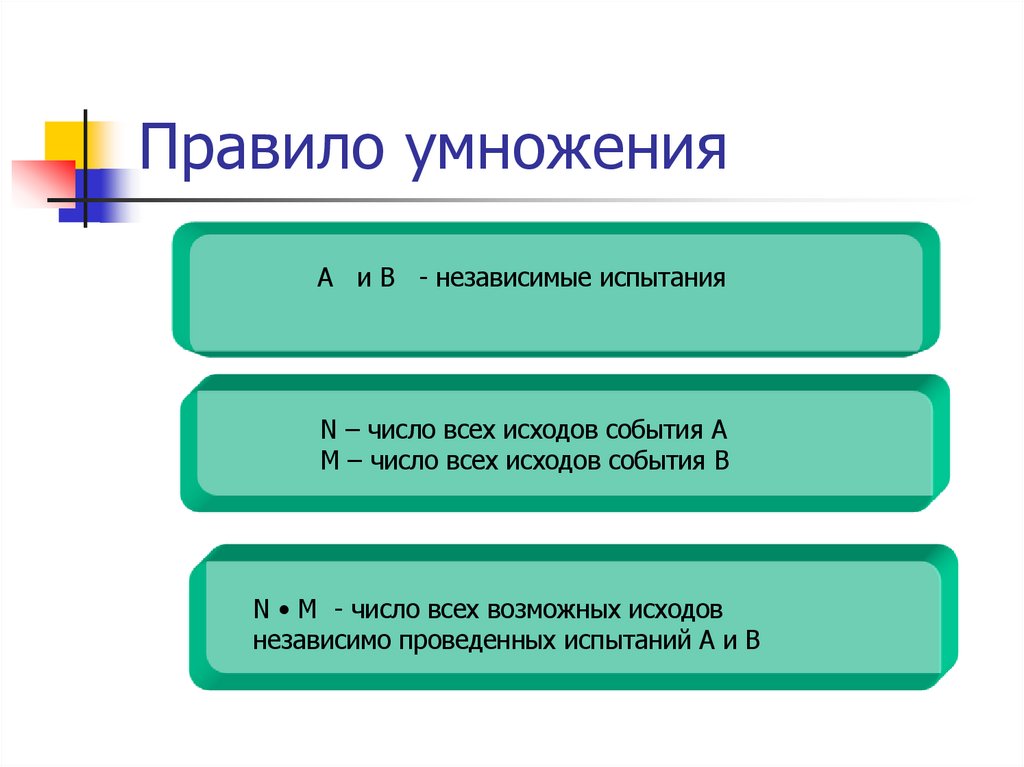
18. Правило умножения
А и В - независимые испытанияN – число всех исходов события А
М – число всех исходов события В
N • M - число всех возможных исходов
независимо проведенных испытаний А и В
19. Задача №4 (самостоятельно)
В случайном эксперименте бросаютдве игральные кости.
Найдите вероятность того, что сумма
выпавших очков меньше 6.
Ответ
округлите до сотых.
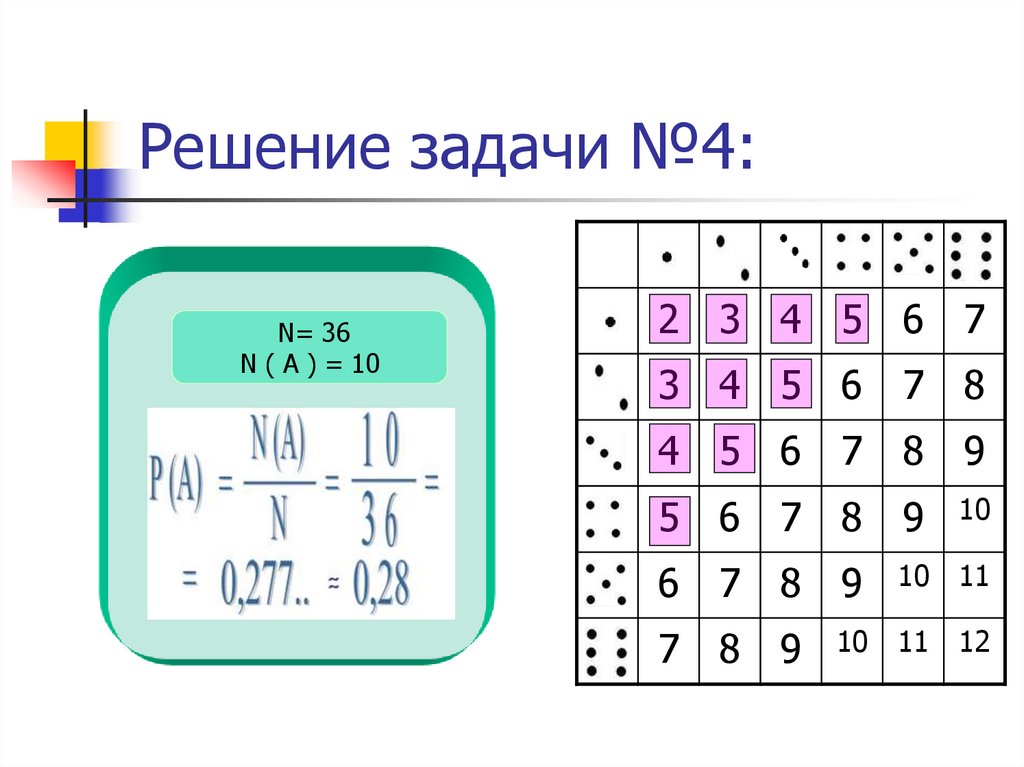
20. Решение задачи №4:
N= 36N ( А ) = 10
2 3 4 5 6 7
3 4 5 6 7 8
4 5 6 7 8 9
5 6 7 8 9
10
6 7 8 9
10
11
10
11
12
7 8 9
21. Свойство вероятности противоположных событий
Напомним:События А и В называются противоположными, если всякое
наступление события А означает ненаступление события В.
Обозначение:
А - событие А
_
А - событие противоположное
событию А (читается «не A»).
Сумма вероятностей противоположных
событий равна :
_
Р(А) + Р(А) = 1
22. Задача №5
В случайном эксперименте бросаютдве игральные кости.
Найдите вероятность того, что сумма
выпавших очков больше 6.
Ответ
округлите до сотых.
23. Решение задачи №5
Событие А : « Выпала сумма большая шести»_
Событие А : « выпала сумма меньшая шести»
Воспользуемся результатом предыдущей задачи:
вероятность выпадения суммы меньшей
шести равна
Тогда:
24. Напомним:
Два событияназываются несовместными в данном
испытании, если появление одного из них
исключает появление другого,
и совместными в противном случае.
Пример:
В мешке находятся 15 шаров: 7 белых, 5 красных и
3 зеленых. Наугад вынимают один шар.
А – шар оказался красным,
В –шар оказался зеленым.
Очевидно: А и В –несовместны.
С – шар оказался не белым (т.е красным или зеленым)
Как связана вероятность события С с вероятностями
cобытий А и В.
Очевидно, что:
25. Правило сложения вероятностей:
26. Задача №6
На учениях летчик получил задание уничтожить три складабоеприпасов. На борту самолета одна бомба.
Вероятность попадания в первый склад 0,1,
Во второй - 0,15,
в третий – 0,2.
Любое попадание в результате детонации
Вызывает взрыв остальных складов.
Найти вероятность того, что склады будут уничтожены.
27. Решение задачи №5:
А –попадание в первый складР(А) = 0,1
В- попадание во второй склад
Р(В)= 0,15
С- попадание в третий склад
Р(С) =0,2
События А, В и С – несовместны.
D- уничтожение складов
По правилу сложения вероятностей:
Р(D)=Р(А)+Р(В)+Р(С)=0,1+0,15+0,2 =0,45
28. Независимые события -если наступление одного не влияет на наступление другого. Например:
В одном мешке находятся10 шариков, из которых
3 зеленых, а в другом
15 шариков, из которых
7 зеленых. Из каждого мешка
наугад вытаскивают по одному
шарику. Какова вероятность
того, что оба шарика окажутся
зелеными?
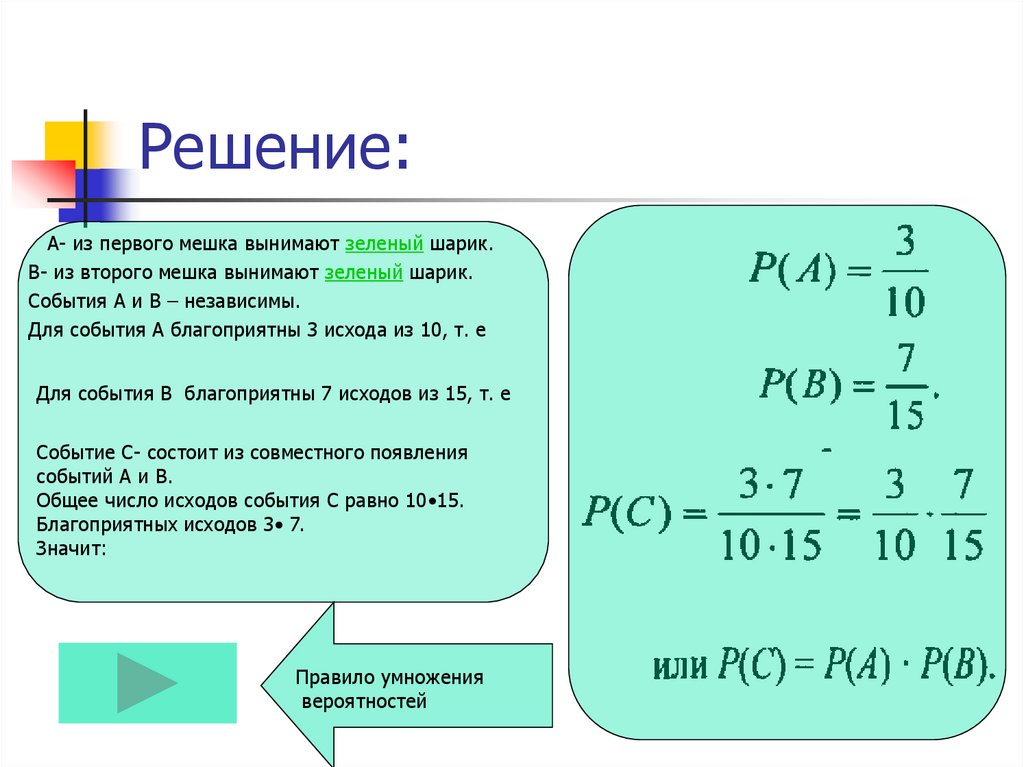
29. Решение:
А- из первого мешка вынимают зеленый шарик.В- из второго мешка вынимают зеленый шарик.
События А и В – независимы.
Для события А благоприятны 3 исхода из 10, т. е
Для события В благоприятны 7 исходов из 15, т. е
Событие С- состоит из совместного появления
событий А и В.
Общее число исходов события С равно 10•15.
Благоприятных исходов 3• 7.
Значит:
Правило умножения
вероятностей
30. Правило умножения вероятностей:
Если событие С означаетсовместное наступление двух
независимых событий событий А и В,
то вероятность вероятность события
С равна произведению вероятностей
события А на событие В.
31. Задача №6
Бросают двеигральные кости.
Какова
вероятность
появления на его
первой кости
четного числа
очков, а на второй
трех очков?
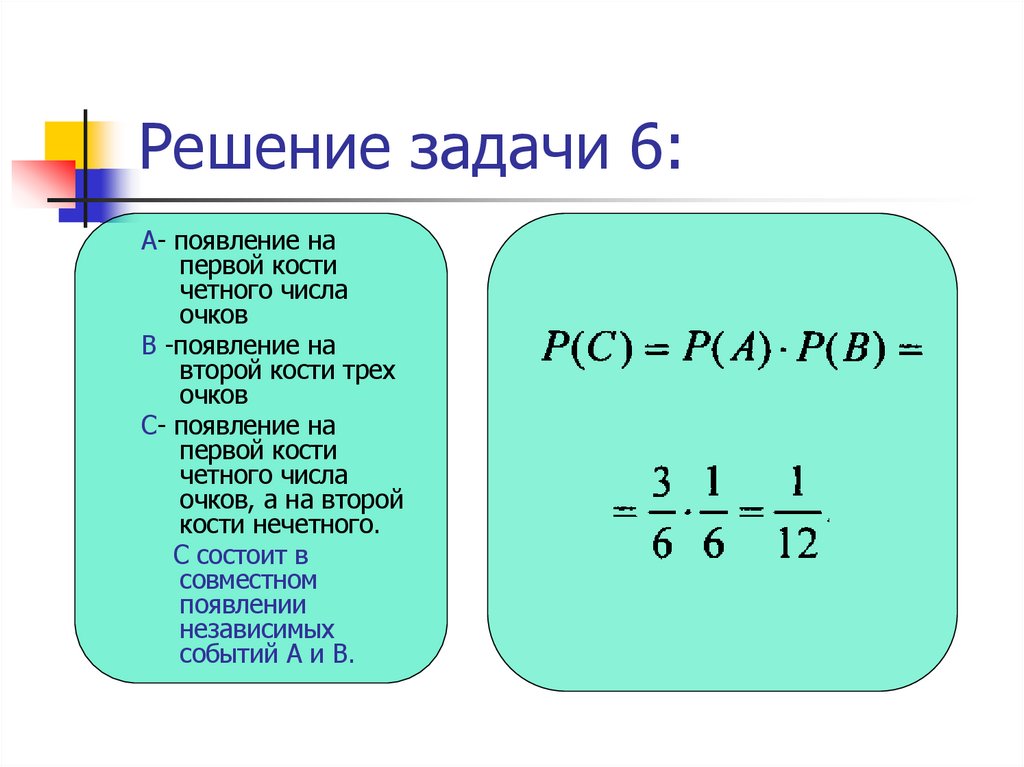
32. Решение задачи 6:
А- появление напервой кости
четного числа
очков
В -появление на
второй кости трех
очков
С- появление на
первой кости
четного числа
очков, а на второй
кости нечетного.
С состоит в
совместном
появлении
независимых
событий А и В.
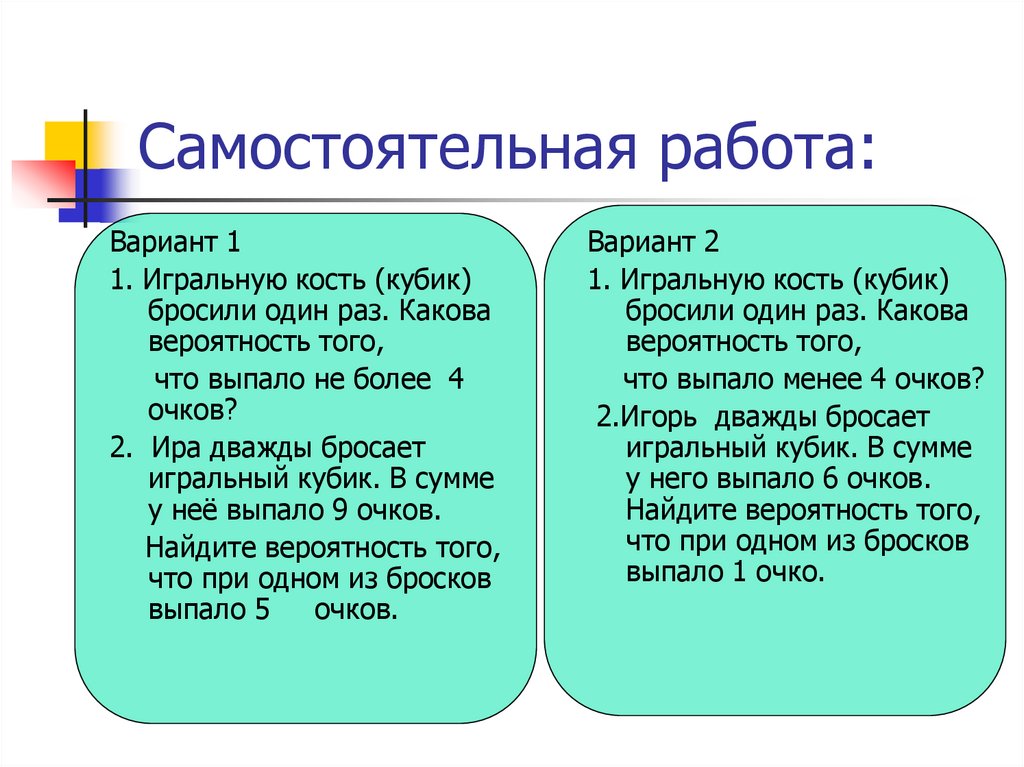
33. Самостоятельная работа:
Вариант 11. Игральную кость (кубик)
бросили один раз. Какова
вероятность того,
что выпало не более 4
очков?
2. Ира дважды бросает
игральный кубик. В сумме
у неё выпало 9 очков.
Найдите вероятность того,
что при одном из бросков
выпало 5
очков.
Вариант 2
1. Игральную кость (кубик)
бросили один раз. Какова
вероятность того,
что выпало менее 4 очков?
2.Игорь дважды бросает
игральный кубик. В сумме
у него выпало 6 очков.
Найдите вероятность того,
что при одном из бросков
выпало 1 очко.
34. Проверка:
Вариант 11. 0,67
2. 0,5
Вариант2
1. 0,5
2. 0,4
35. Ответьте на вопросы:
1.2.
3.
4.
5.
Какие события называют
несовместными?
Правило сложения вероятностей.
Свойство вероятностей
противоположных событий.
Какие события называются
независимыми?
Правило умножения вероятностей.
36. Домашнее задание:
Конспект№ 51.2, 51.6,51.8
37. Литература:
А.Г. Мордкович Алгебра 9 класс: Учебник для общеобразовательных учреждений – М.: Мнемозина, 2011;А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. Алгебра 9 класс. Задачник для общеобразовательных
учреждений – М.: Мнемозина, 2009;
Л.А. Александрова Алгебра 9 класс: Самостоятельные работы для общеобразовательных учреждений. – М.:
Мнемозина, 2011;
Энциклопедия. Я познаю мир. Великие ученые. – М.: ООО «Издательство АСТ», 2003;
Г. Мордкович А.Г. Алгебра 7-9 Методическое пособие для учителей. – М.: Мнемозина, 2009;
http://ru.wikipedia.org/
http://persons-info.com
Картинки:
http://clipartsign.com/upload/2016/04/04/dice-adobe-illustrator-tutorials-for-creating-excellent-vector-clipart.jpg
http://labs.openviewpartners.com/wp-content/uploads/files/2012/08/coin_toss.jpg
https://rentmania.org/images/photos/large/6182-4182_hTFbFcfhDb4.jpg?1463141032
http://in-print.ru/arc/kartyigra000l.jpg



























 mathematics
mathematics








