Similar presentations:
Простейшие вероятностные задачи
1. Простейшие вероятностные задачи.
ПРОСТЕЙШИЕ ВЕРОЯТНОСТНЫЕЗАДАЧИ.
2. Понятие вероятности
Вероятностью события называется число,Понятиекакую
вероятности
показывающее
часть составляют
исходы
испытания,
в
которых
наступает
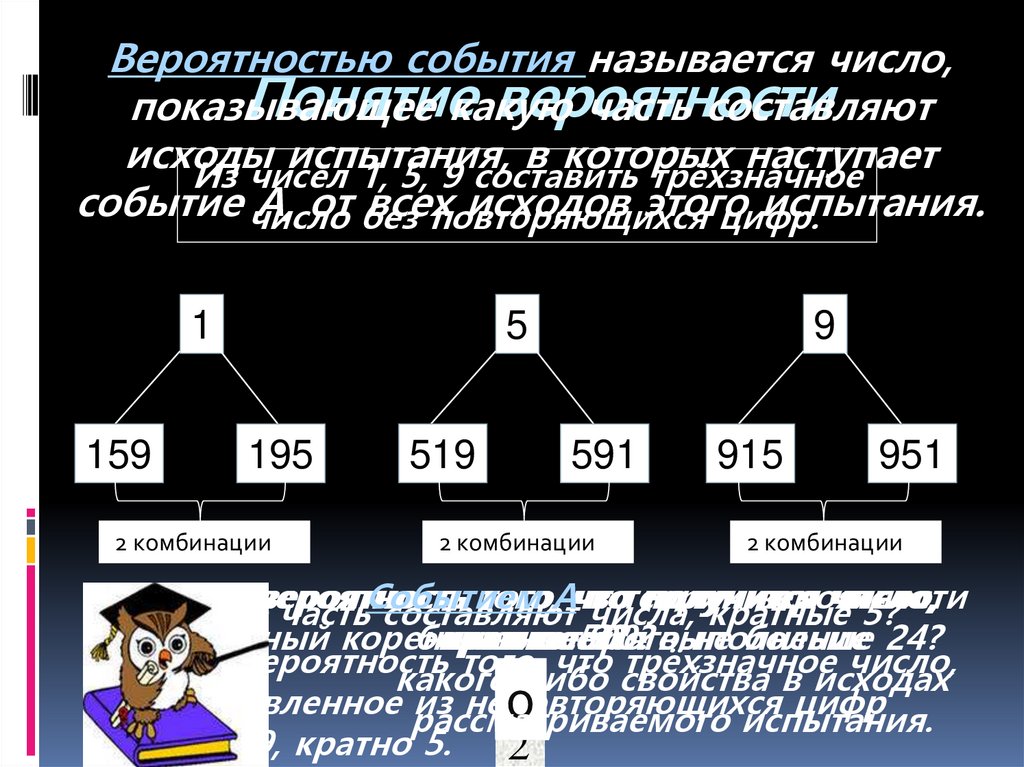
Из чисел 1, 5, 9 составить трёхзначное
событие число
А, от без
всех
исходов этого
испытания.
повторяющихся
цифр.
1
159
5
195
2 комбинации
519
9
591
2 комбинации
915
951
2 комбинации
Какова
Какова
вероятность
того,
того,Ачто
что
в теории
получится
получится
вероятности
число,
число,
Какуювероятность
частьСобытием
составляют
числа,
кратные
5?
большее
кратное
кратное
называется
из которого
500?
9?
3? выполнение
не больше 24?
1квадратный корень
-это вероятность того, что трёхзначное число,
свойства в исходах
2
3 составленноекакого-либо
1
из неповторяющихся
цифр
0
13
рассматриваемого
испытания.
1, 5, 9, кратно 5.
2
3. События.
Достоверное событие - это событие,происходящее в любом случае.
Вероятность достоверного события
равна 1.
Невозможное событие - это событие,
никогда не происходящее.
Вероятность невозможного события
равна 0.
Случайное событие - это событие,
которое может как наступить, так и
не наступить.
4. «Орлянка»
Равновозможными событиями называютсяМИНЗДРАВ ПРЕДУПРЕЖДАЕТ!!!
события, вероятность
появления
которых
«Азарт
ные
игры
вызывают
«Орлянка»
одинакова.
психические
заболевания!!!»
Задача 1.
Монету подбрасывают три раза. Какова вероятность
того, что: а) все три раза выпадет «решка»;
б) «решка» выпадет в 2 раза чаще, чем «орёл»;
в) «орёл» выпадет в 3 раза чаще, чем «решка»;
г) при первом и третьем подбрасывании результаты
будут различны?
ООО
ООР
ОРО
ОРР
РОО
РОР
РРО
РРР
Какова
вероятность
того,
что
при
первом
ираза
третьем
3 10 того,
Какова
Какова
Какова
вероятность
вероятность
вероятность
того,
того,
что
что
что
все
«решка»
«орёл»
3
0 ,375
0,5 будут различными?
0,
125
подбрасывании
результаты
выпадет
выпадетвв
выпадет
32раза
разачаще,
чаще,
«решка»?
чем
чем«решка»?
«орёл»?
8 2
5.
Классическоеопределение
Классическая
вероятностная
схема.
вероятности.
N ( A)
P ( A)
N
Для нахождения вероятности случайного события
при проведении некоторого испытания следует:
Вероятностью события А называется отношение
1) Найти число N всех возможных исходов данного
числа
тех
исходов,
в
результате
которых
испытания.
наступает событие А, к общему числу всех
2) Найти
число N(А) тех исходов
испытания,
(равновозможных
между
собой) в
которых наступает
событие
А.
исходов
испытания.
3)Найти отношение
N ( A) ; оно и будет равно
N
вероятности события А.
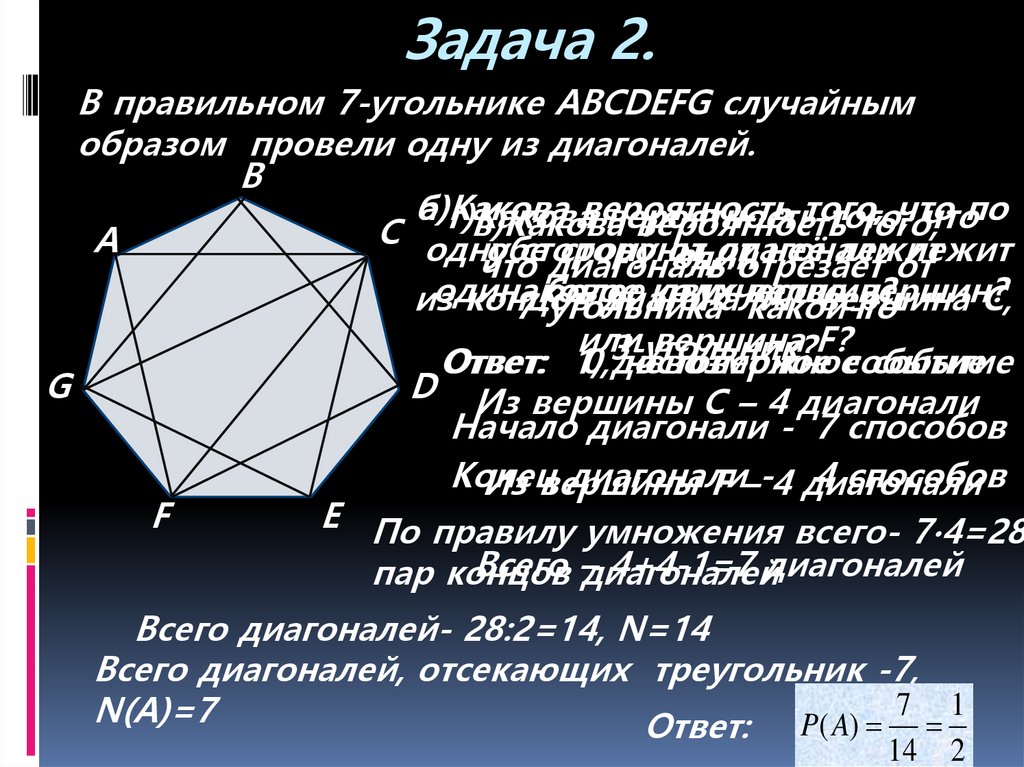
6. Задача 2.
В правильном 7-угольнике ABCDEFG случайнымобразом провели одну из диагоналей.
В
б)Какова
а)Какова
вероятность
того,
что
по
г)Какова
вероятность
того,
что
в)Какова
вероятность
того,
С одну
А
обе
сторону
стороны
от
диагонали
ототрезает
неё лежит
лежит
один
что
диагональ
от
одинаковое
более
количество
двух вершин?
вершин?
из
концов
диагонали
- вершина
С,
7-угольника
какой-то
или
вершина F?
3-угольник?
Ответ: 1,
0, достоверное
невозможноесобытие
событие
G
D Из вершины С – 4 диагонали
Начало диагонали - 7 способов
Конец
диагонали
4 способов
Из вершины
F –-4 диагонали
F
E По правилу умножения всего- 7∙4=28
Всего –диагоналей
4+4-1=7 диагоналей
пар концов
Всего диагоналей- 28:2=14, N=14
Всего диагоналей, отсекающих треугольник -7,
7 1
N(A)=7
Ответ: P( A)
14
2
7. Задача 3.
Из 50 шаров 17 окрашены в синий цвет, 13в оранжевый, остальные в другие цвета.Какова вероятность того, что случайным
образом выбранный шар окажется:
г)ни синим,
синим
,или
ни оранжевым?
в)или
б)не а)синим;
оранжевым;
оранжевым;
NN50
((синорш
неорш
N
(17
сш )))1317
)50
17 20
13
13 30
PPР Р
0,34
00,4,74 0,6
NN
50
50 50
50
50
50
8. Несовместные и противоположные события.
Определение 1.2.
Определение
Теорема
Теорема 2.
1.
СобытиеДля
В называется
нахождения
противоположным
вероятности
событию
противоположного
А, если событие
В происходит
надо то
изте1
Если события
А и В события
несовместны,
Несовместными
событиями
называют
тогда
вычесть
и только
вероятность
тогда,
самого
непроисходить
происходит
события:
вероятность
того,
что
наступит
или
события,
которые
некогда
могут
событиеА А;
обозначают
В=А. вероятностей
событие
, или
ВР(А)=1-Р(А).
равна сумме
одновременно.
А и В. Р(А+В)=Р(А)+Р(В)
9. Задача 4.
МИНЗДРАВ ПРЕДУПРЕЖДАЕТ!!!«Азарт ные
игры вызывают
Задача
4.
психические заболевания!!!»
Какова вероятность того, что при трёх
Вероятностьбросаниях
выпадения
6
последовательных
игрального
кубика
хотя бы один раз
выпадет 6.
Р(А)=91:216
≈0,4213
Событие А- выпадение 6.
Событие
А :6 не выпадает
вообще,
ни в первый,
При первом
бросании-6
возможных
исходов
ни во второй, ни в третий раз.
При втором бросании-6 возможных исходов
За три бросания всего 5∙5∙5=125 возможных
Второй
способ:
При
третьем
бросании-6
возможных
исходов
исходов
события
А.
За три бросания всего 6∙6∙6=216
125 возможных
91
Р( А) 1 Р
( А) 1
исходов.
216
216
Число исходов события А N(A)=216-125=91.
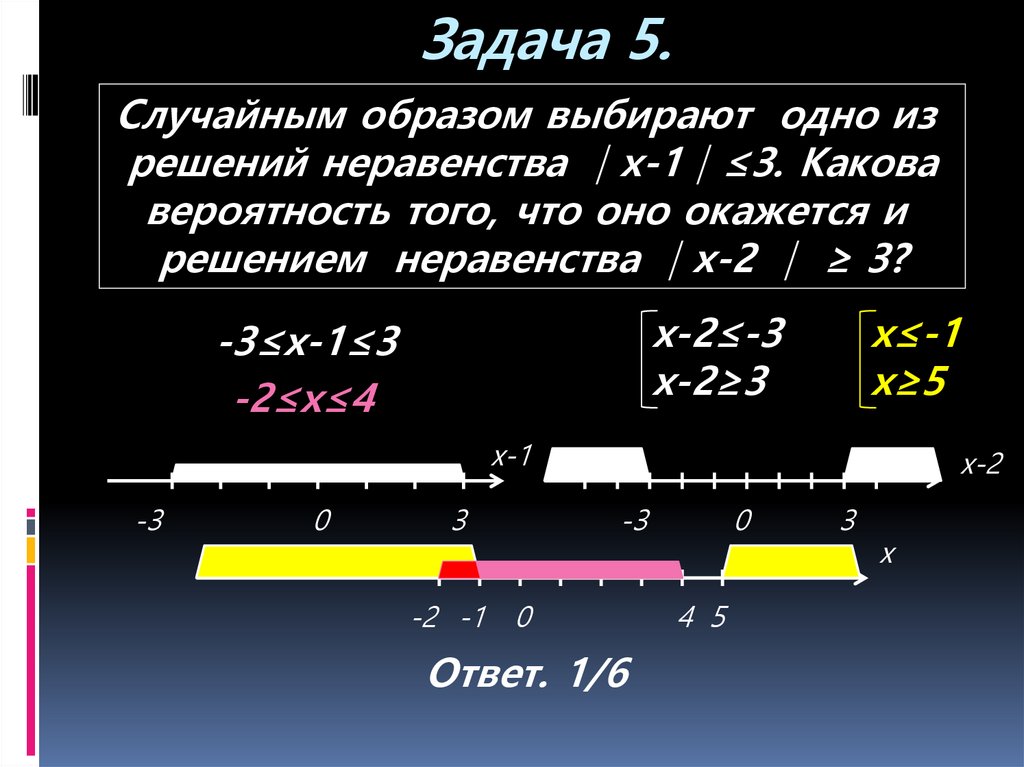
10. Задача 5.
Случайным образом выбирают одно изрешений неравенства │x-1│≤3. Какова
вероятность того, что оно окажется и
решением неравенства │x-2 │ ≥ 3?
х-2≤-3
х-2≥3
-3≤х-1≤3
-2≤х≤4
х≤-1
х≥5
х-1
-3
0
3
х-2
-3
-2 -1 0
Ответ. 1/6
0
4 5
3
х
11. Задача 6.
CГрафический редактор, установленный на
компьютере, случайно отмечает одну точку
на мониторе – квадрате АВСD со стороной
12см. Какова вероятность того, что эта точка:
B б) окажется
одновременно
в)будет удалена
от
а) окажется в верхней
в нижней
и левой
вершины
Dмонитора?
не
более,
половине
части
монитора?
чем на
11см ?
S ABCD
1 144
2
S1/ 4 круга 112 30,25
4
SS
6 72
36
1/ 1
4 ABCD
/ 2 ABCD
А
D
72 1
Р 30,25
0,5
36
1 0,66
Р
144
2
Р
0,25
144
144
4
12. Правило нахождения геометрической вероятности.
ХА
Если фигура Х целиком
содержит в себе фигуру
А, то вероятность того,
что точка, случайно
выбранная из фигуры Х,
принадлежит фигуре А
равна отношению
площади фигуры А к
площади фигуры Х.
S ( A)
Р
S(X )









 mathematics
mathematics








