Similar presentations:
Решение систем рациональных уравнений
1.
2.
Работу выполнилаКЛЁСОВА ОЛЬГА
11 Б
3.
Руководители:Полякова Р.В.
Учитель математики
Клёсова Н.К.
Учитель информатики
4.
5.
6.
Подстановкачисел
из ОДЗ
7.
f(x)>Ag(x)<A
f(x)=g(x)
Решений нет
----------------------------------------------f(x) A
g(x) A
f ( x ) A
f(x)=g(x)
g ( x ) A
8.
f(x)Непрерывная и строго монотонная
на промежутке Х
f(x)=a
Не более одного решения
-----------------------------------------------f(x) - строго возрастает
f(x)=g(x)
g(x) - строго убывает
Не более одного решения
9.
f(x)Строго возрастающая
функция
f(f(x))=x
f(x)=x
10.
Пример 1.y x 2y 1 3
2
y y 2 ( y 4) 5
--------------------------y 3 x 2y 1
x 2y 1 0
2
y y 2 ( y 4) 0
или
y 3
2
( y 3) 0
y x 2y 1 3,
y 3,
y=5, x=3
Ответ: (3;5).
11.
Уравнение 1.Пример 2. 2
2 4xy 2x 6y 2 0,
x
5
y
3x 2 2y 2 xy 3x 2y 1 0.
Уравнение 2.
-------------------------------
Уравнение 1.
x 2 2x( 2y 1) 5 y 2 6y 2 0
2
D ( y 1) 0
x 1, y 1
Ответ: (1;1)
Уравнение 3.
Уравнение 4.
Уравнение 2.
Уравнение 3.
12.
Уравнение 1.Пример 3. y 2 ( 3 x )2 ,
( 2z y )( y 2) 9 4 y ,
2
2 4x 2 .
x
z
---------------------------
2 y 2,
(
3
x
)
2 2z 0,
z
2 z 2 2z ,
(
y
3
z
)
( x 2 ) 2 4 z 2 .
x=2, y=-1, z=2
Ответ: (2;-1;2).
Уравнение 3.
Уравнение 4.
Уравнение 1.
Уравнение 2.
Уравнение 3.
2
4 z 0
z 0
x=4, y=-3, z=2
Уравнение 2.
13.
Пример 4. x 2y 2 5x 2 4 0,x 7 x 4 5x y 7 y 4 5 y .
----------------------------7
4
f ( x ) x x 5x
6
3
f ( x ) 7 x 4x 5
( t ) 7 t 2 4t 5
D 0
Уравнение 1.
Уравнение 2.
Уравнение 3.
Уравнение 4.
Уравнение 1.
Уравнение 2.
Уравнение 3.
f (x ) 0
f(x) является возрастающей для всех Х
f (x) f ( y )
14.
Уравнение 1.2 2
x y 5x 2 4 0,
y x.
Уравнение 2.
x 4 5x 2 4 0
Уравнение 1.
x 1,x 2
Уравнение 3.
Уравнение 4.
Уравнение 2.
Уравнение 3.
(1;1), (-1;-1), (2;2), (-2;-2)
Ответ: (1;1), (-1;-1), (2;2), (-2;-2)
15. Указание к применению метода
• Разработанный метод применять, когда• алгебраическое выражение в условии задачи разбивается на
группы одинаковых по виду членов, которые можно выразить с
помощью одной и той же функции, обладающей простыми
свойствами.
• одно из уравнений в системе удается представить в виде
композиции одной функции,причем одна из которых взрастает.
Иногда для такого представления необходимо проделать
тождественные преобразования.
• если в одном из уравнений участвуют функции с хорошо
известными свойствами (монотонность, ограниченность)
16.
17.
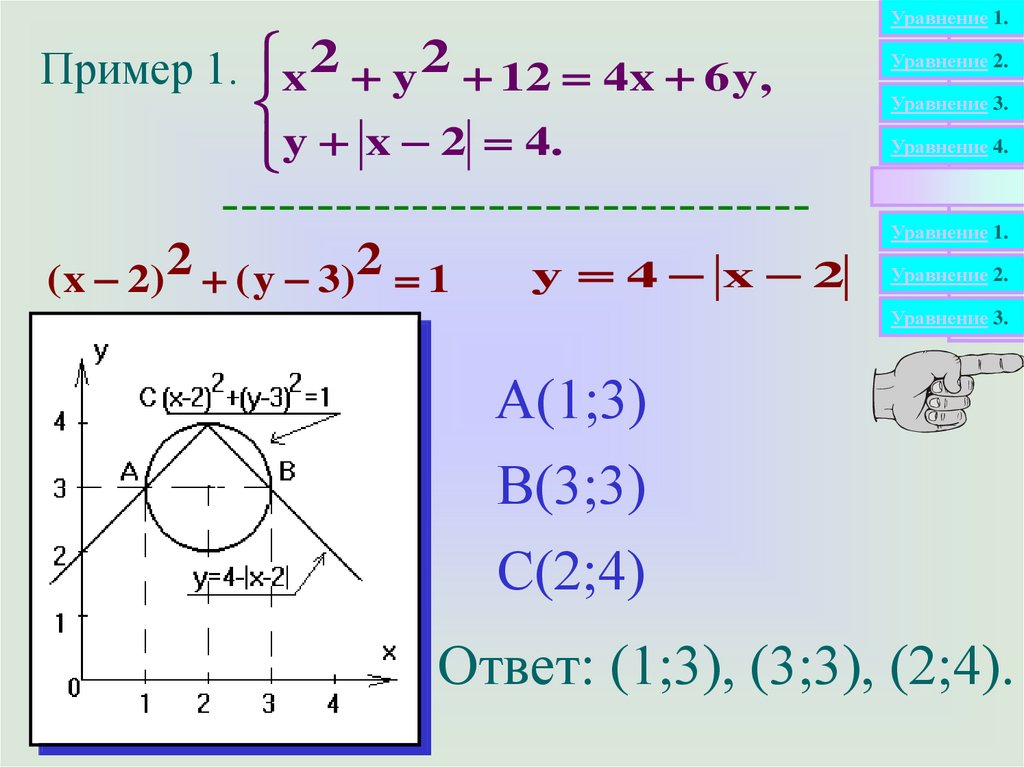
Пример 1.x 2 y 2 12 4x 6 y ,
y x 2 4.
------------------------------( x 2) 2 ( y 3) 2 1
y 4 x 2
Уравнение 1.
Уравнение 2.
Уравнение 3.
Уравнение 4.
Уравнение 1.
Уравнение 2.
Уравнение 3.
А(1;3)
В(3;3)
С(2;4)
Ответ: (1;3), (3;3), (2;4).
18.
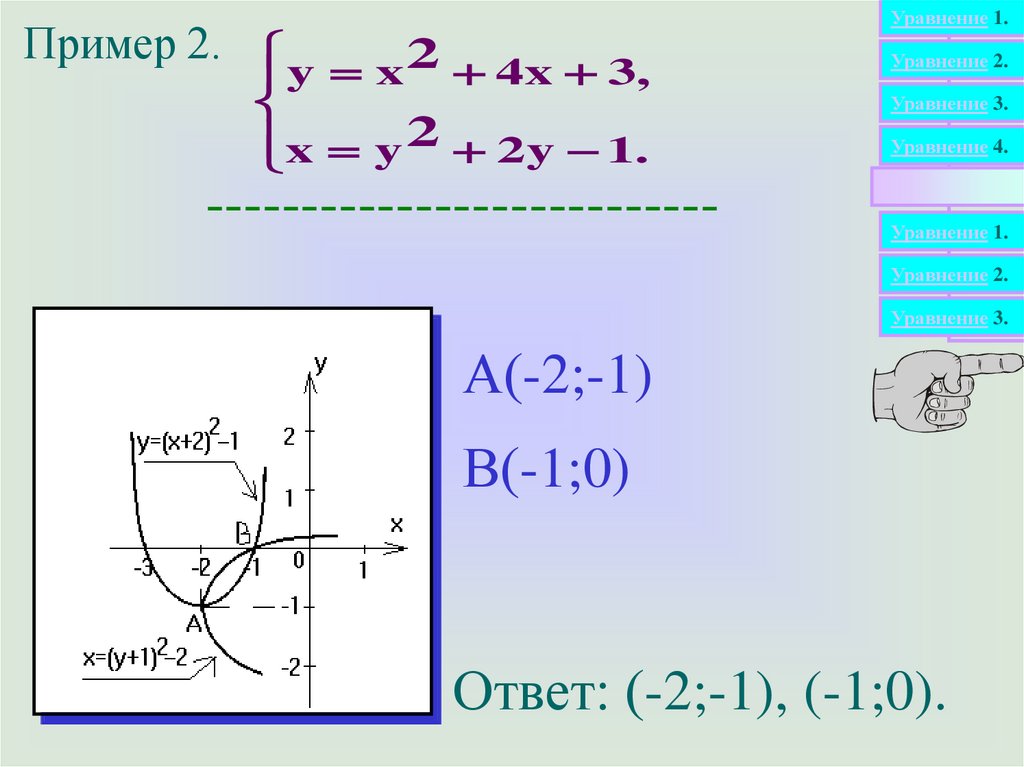
Пример 2.2 4x 3,
y
x
x y 2 2 y 1.
---------------------------
Уравнение 1.
Уравнение 2.
Уравнение 3.
Уравнение 4.
Уравнение 1.
Уравнение 2.
Уравнение 3.
А(-2;-1)
В(-1;0)
Ответ: (-2;-1), (-1;0).
19.
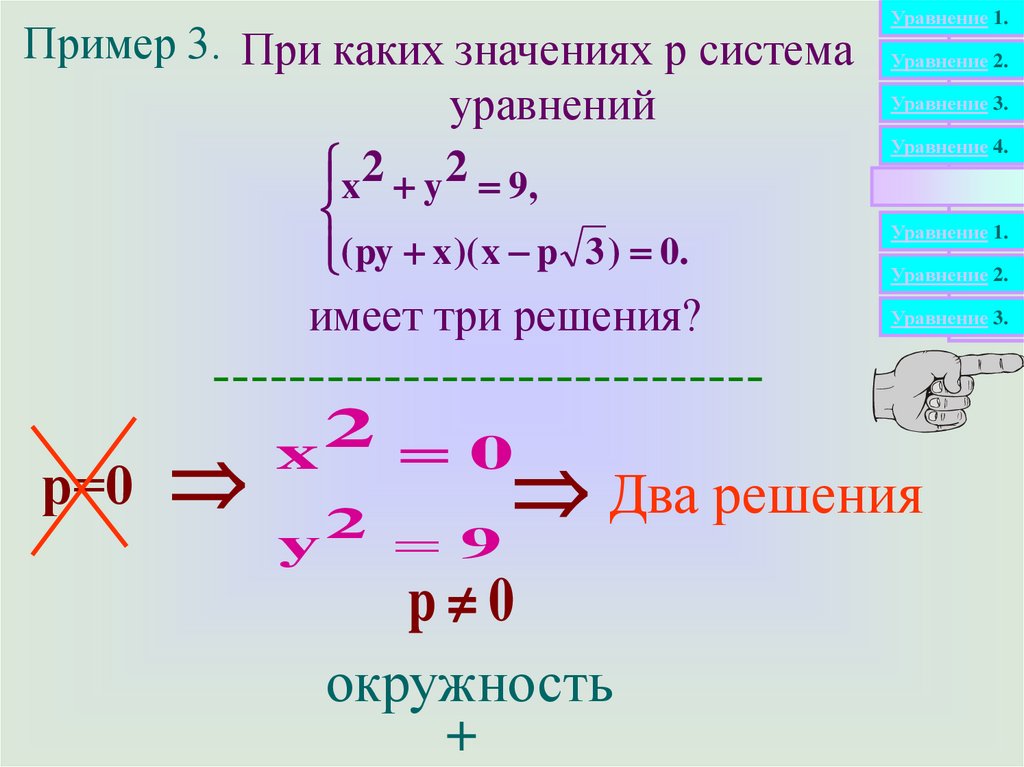
Пример 3. При каких значениях р системауравнений
2
x y 2 9,
Уравнение 1.
Уравнение 2.
Уравнение 3.
Уравнение 4.
( py x )( x p 3 ) 0.
Уравнение 1.
имеет три решения?
Уравнение 3.
Уравнение 2.
----------------------------2
x
0
р=0
Два
решения
2
y
9
p 0
окружность
+
20.
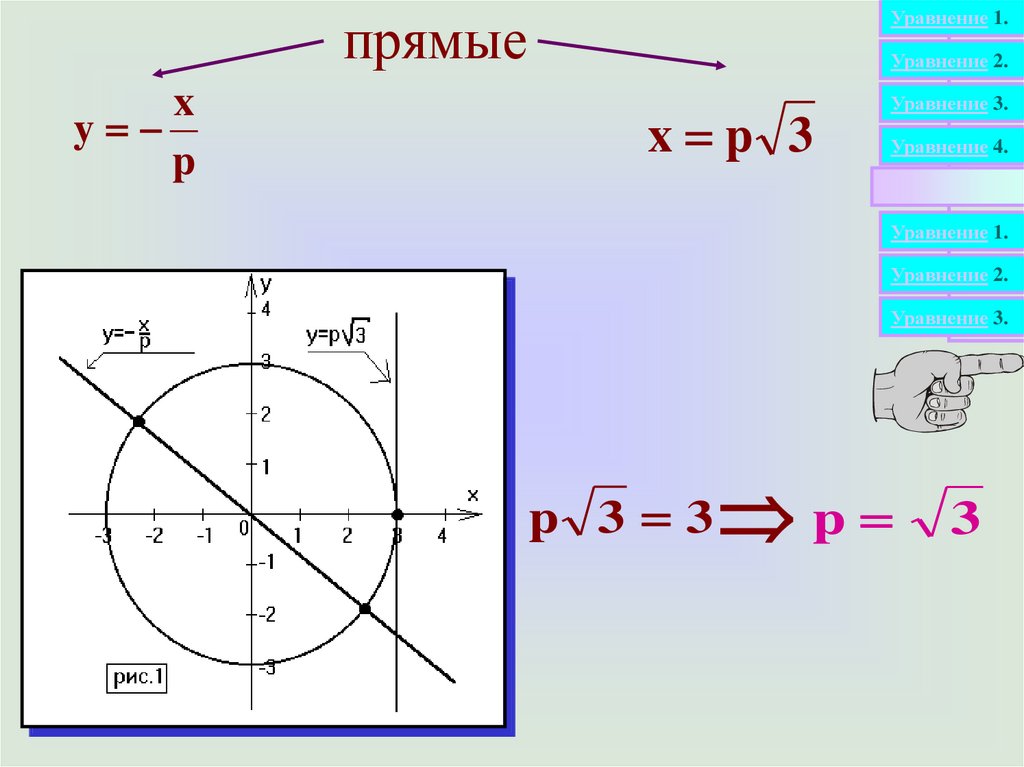
Уравнение 1.прямые
x
y
p
Уравнение 2.
x p 3
Уравнение 3.
Уравнение 4.
Уравнение 1.
Уравнение 2.
Уравнение 3.
p 3 3
p 3
21.
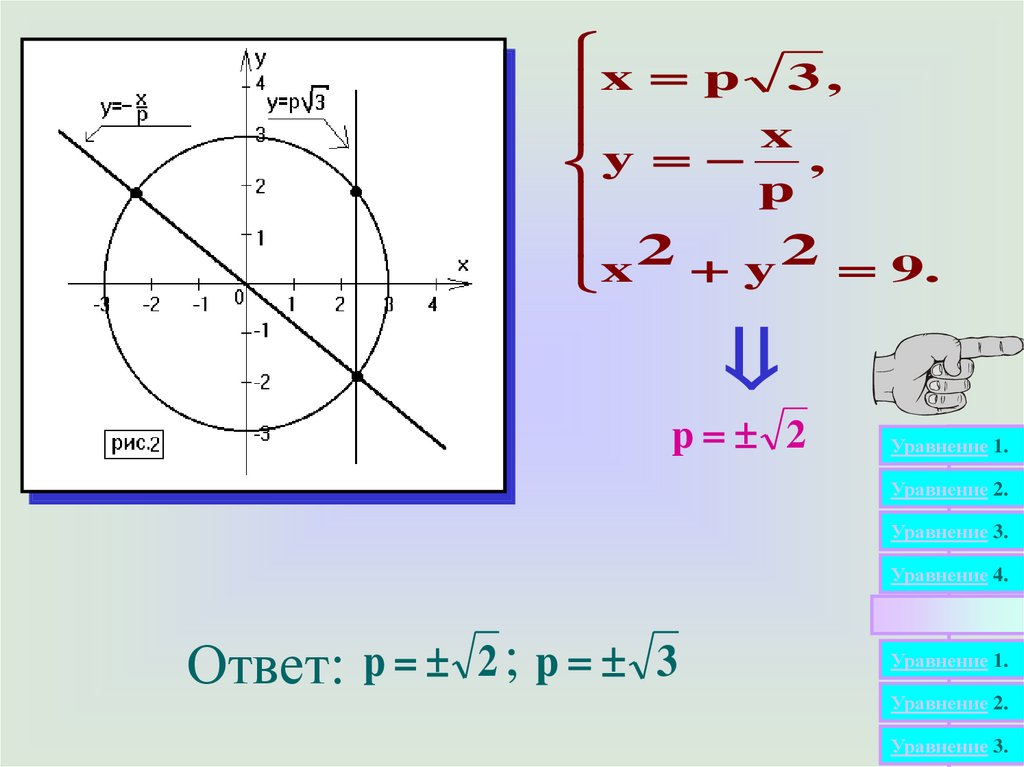
x p 3 ,x
,
y
p
2
2 9.
x
y
p 2
Уравнение 1.
Уравнение 2.
Уравнение 3.
Уравнение 4.
Ответ: p 2 ; p 3
Уравнение 1.
Уравнение 2.
Уравнение 3.
22.
Спасибоза внимание!









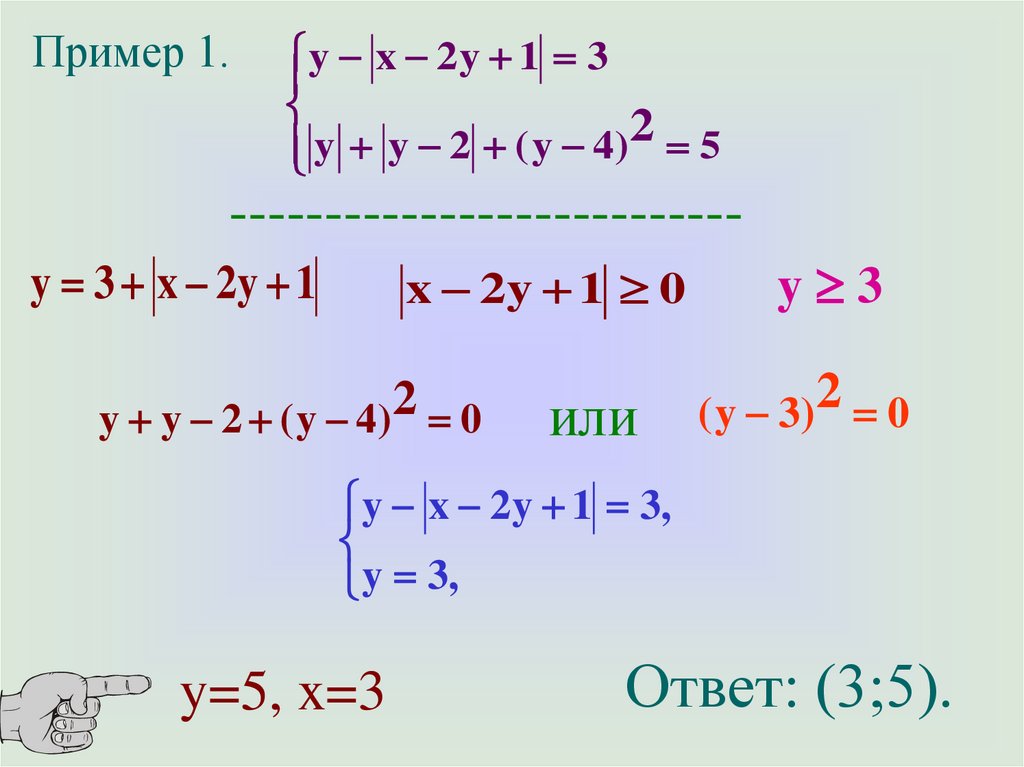







 mathematics
mathematics








