Теоретические основы электротехники

1.

«Теоретические основы электротехники»
Доктор технических наук, профессор ПШ ЮГУ
Осипов Дмитрий Сергеевич
Ханты-Мансийск, 2024

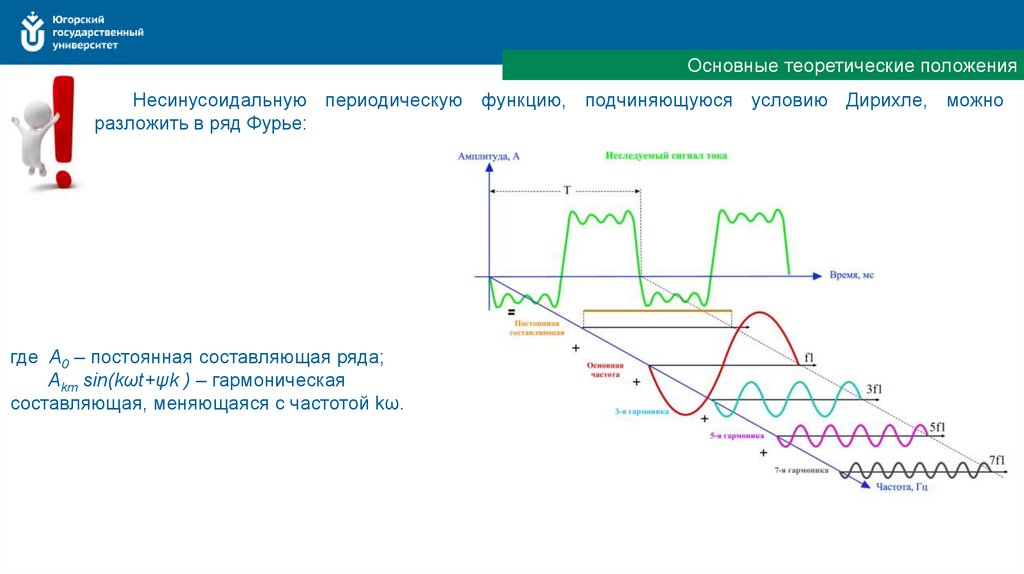
Основные теоретические положения
Несинусоидальную периодическую функцию, подчиняющуюся условию Дирихле, можно
разложить в ряд Фурье:
где А0 – постоянная составляющая ряда;
Akm sin(kωt+ψk ) – гармоническая
составляющая, меняющаяся с частотой kω.

4.

Основные теоретические положения
Источник несинусоидальной ЭДС представляют как ряд последовательно соединенных
источников ЭДС, источник несинусоидального тока – как ряд параллельно соединенных источников
тока с разной частотой.

5.

Основные теоретические положения
При расчете применяют метод наложения. Рационально разбить схему на столько подсхем,
сколько частот получается при разложении в ряд Фурье несинусоидальных ЭДС и токов.
Подсхемы отличаются друг от друга не только источниками энергии, но и величинами
реактивных сопротивлений, которые зависят от частоты:
Мгновенные значения токов и напряжений в схеме получают суммированием соответствующих
мгновенных значений в подсхемах.
Действующие значения токов, напряжений и ЭДС определяют через соответствующие действующие
значения в подсхемах по формулам:

6.

Пример 1
Найти законы изменения токов i1 и i2 в цепи, схема замещения
которой представлена на рисунке, если
i
~u
В
i1
i2
Ом
мкФ
мГн
Гц

7.

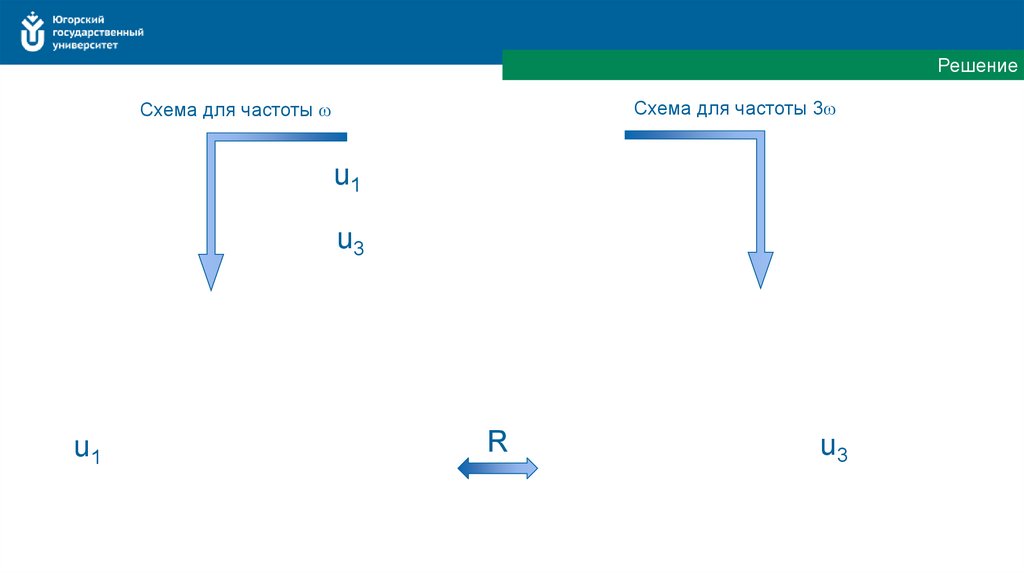
Решение
Схема для частоты 3ω
Схема для частоты ω
u1
u3
u1
R
u3

8.

Решение
Рассмотрим схему на основной частоте (1ω)
Комплексная величина максимального напряжения:
В
u1
i(1)
Индуктивное сопротивление:
i(2)
Ом
Ёмкостное сопротивление:
Ом
Комплексная величина максимального тока в первой (1) ветви (ёмкость и индуктивность):
А

9.

Решение
Комплексная величина максимального тока в второй (2) ветви (резистор):
А
Мгновенные токи в первой и второй ветви:
А
А

10.

Решение
Рассмотрим схему на третьей гармонике (3ω)
Комплексная величина максимального напряжения:
В
u3
i(1)
Индуктивное сопротивление:
i(2)
Ом
Ёмкостное сопротивление:
Ом
Комплексная величина максимального тока в первой (1) ветви (ёмкость и индуктивность):
А

11.

12.

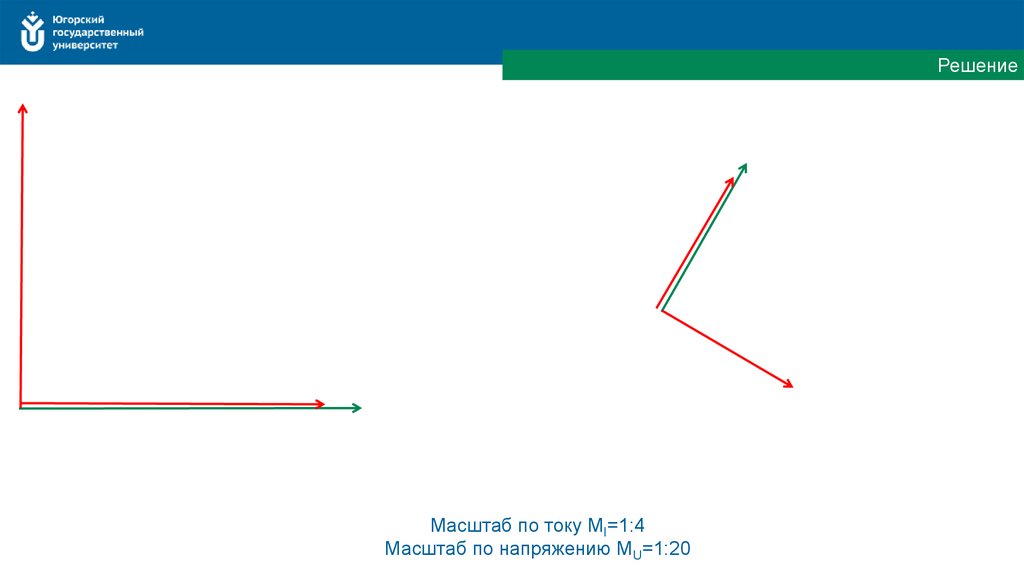
Решение
Масштаб по току MI=1:4
Масштаб по напряжению MU=1:20

13.

Решение
Мгновенные токи в первой и второй ветви в виде ряда Фурье (сумма гармоник):
А
А

14.

Пример 1
A
iA
C
eA
N
n
C
eB
eC
B
C
a
c
C
iC
iB
Дано: eA=150sin ωt + 30sin(3ωt + 30°) +18sin(5ωt − 30°) (В)
C=106,2 (мкФ)
ω≈314 (рад/с)
Найти: мгновенные значения токов iA iB iС; показания вольтметров
b

15.

Решение
1. ЭДС источника задана в виде суммы гармонических составляющих (высших гармоник), что
моделирует несинусоидальный режим работы сети. Для расчета несинусоидальных режимов можно
воспользоваться принципом наложения.
Для первой подсистемы (основная частота ω):
eA=150sin ωt
eB=150sin (ωt − 120°)
eC=150sin (ωt + 120°)

16.

Спасибо за внимание! Ваши вопросы
Осипов Д.С.
+7 922 444 38 99
[email protected]

English Русский Rules