Вычислительные алгоритмы. Погрешности (лекция 4)

1. Вычислительные алгоритмы

Александр Владимирович Иванов,
к.э.н.
1

2. Лекция 4.

3. Погрешности

1. Погрешности
Рассмотрим выражение 8a+2b. Пусть a и b имеют одинаковую абсолютную
погрешность .
Какое слагаемое внесет больший вклад в относительную ошибку и во сколько раз?
2. Погрешности
В первом числе две точных значащих цифры 3,7. Во втором - четыре 3,768.
Перемножьте их, оставив в произведении обоснованное число значащих цифр.

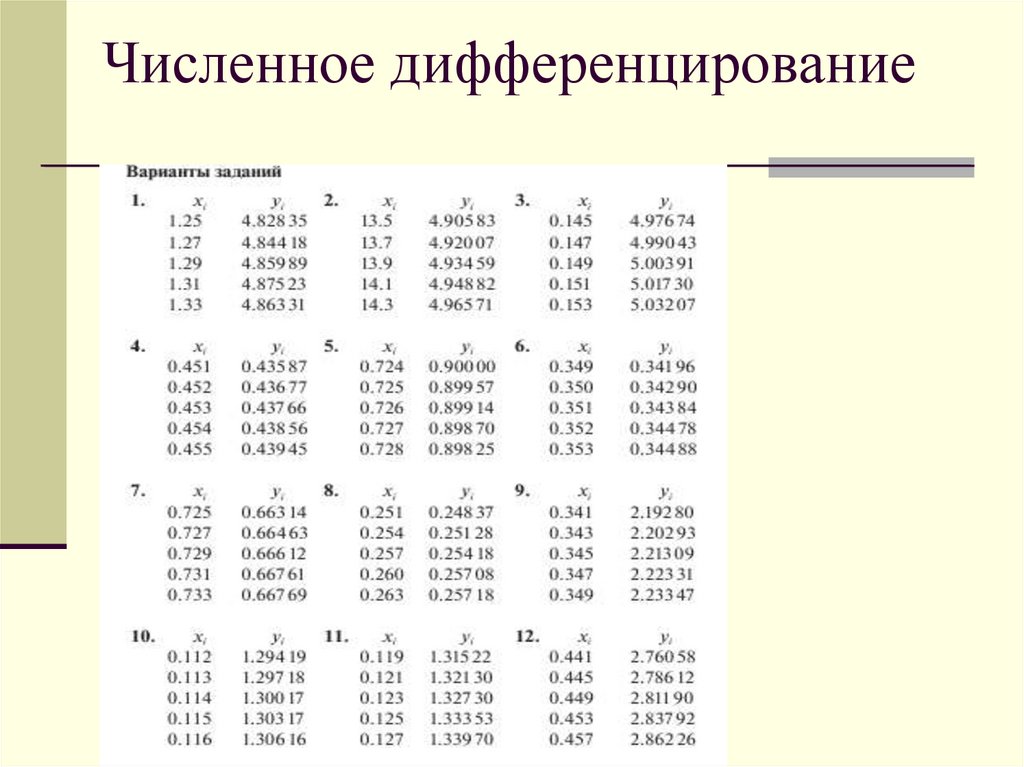
4. Численное дифференцирование

Использовать формулы для расчета первой производной по 4 узлам

5. Численное дифференцирование

6. Алгоритм расчета интеграла

Выполнить расчет интеграла по формуле трапеций
В качестве исходных данных взять вариант для расчета
производной

7. Алгоритм решения системы линейных уравнений методом Гаусса

Пусть имеется два пункта вывоза продукции и три пункта их
реализации. Производимая продукция точно равна реализуемой
продукции. В первом пункте производится 130 изделий в сутки во
втором 70. В первом пункте реализации реализуется 50 изделий, во
втором 90, в третьем 60.
x11+x12+x13=130
x21+x22+x23=70
x11+x21=50
x12+x22=90
x13+x23=60
(Шесть переменных и 5 уравнений)

8. Алгоритм решения системы линейных уравнений методом Гаусса Продолжение

Расстояния от первого пункта производства до пунктов реализации равно до первого
пункта реализации 9 км, до второго - 5 км и до третьего - 7 км. Расстояния от второго
пункта производства до пунктов реализации равны, соответственно, 4, 8 и 6 км.
Цель расчетов заключается в минимизации целевой функции, равной
f=9*x11+5*x12+7*x13+4*x21+8*x22+6*x23
где xij – количество изделий, перевозимых из i-того пункта производства в j-тый пункт
реализации.
Алгоритм решения заключается в переборе возможных значений xij и нахождении
минимума целевой функции f.
а) Для того, чтобы решить систему из 5 уравнений, необходимо одну из переменных
приравнять либо к нулю, либо к максимуму, равному 130, 70, 50, 90, 60. Для каждого
решения найти значение целевой функции и выбрать среди них минимальное значение.
б) Для решения получившейся после исключения шестой переменной системы из 5
уравнений для 5 переменных предлагается использовать метода Гаусса –
последовательного исключения неизвестных.
разработать алгоритм на языке программирования и найти минимальное значение
целевой функции.

9. Условия задачи

УСЛОВИЯ ЗАДАЧИ
Пусть известны возможные варианты и их исходы.
Вероятность каждого исхода равна 1.
Пусть имеются два альтернативных варианта.
Критерий – прибыль для чисто экономического проекта –
достижение наиболее высокого уровня безопасности для
экологического проекта. Сравниваются два проекта на
соответствие этому критерию.
В этом случае:
• определяется критерий отбора
• методом прямого счета вычисляется значение
критерия
• вариант с лучшим значением критерия рекомендуется
к отбору.

10. План Лекции 5 Конкретизация задачи

ПЛАН ЛЕКЦИИ 5
КОНКРЕТИЗАЦИЯ ЗАДАЧИ
Пусть предприятие принимает на переработку f тонн
первого вида отходов и x тонн второго вида отходов. Пусть
затраты логистического подразделения в расчете на одну
тонну этого отхода составят 100 $, затраты второго
подразделения – 200 $ на тонну. Затраты по второму виду
отходов составляют, соответственно, 300 $ в первом
подразделении и 100 $– во втором подразделении. Бюджет
первого подразделения составляет 40000 $ , второго
30000 $. Прибыль от продажи тонны готовой продукции
полученной из первого отхода составит 400 $ за тонну,
прибыль от продажи продукта из второго отхода составляет
500 $ за тонну. Сколько отходов первого и второго вида
следует взять на переработку для получения максимальной
прибыли.

11. План Лекции 5 Конкретизация задачи 2

ПЛАН ЛЕКЦИИ 5
КОНКРЕТИЗАЦИЯ ЗАДАЧИ 2
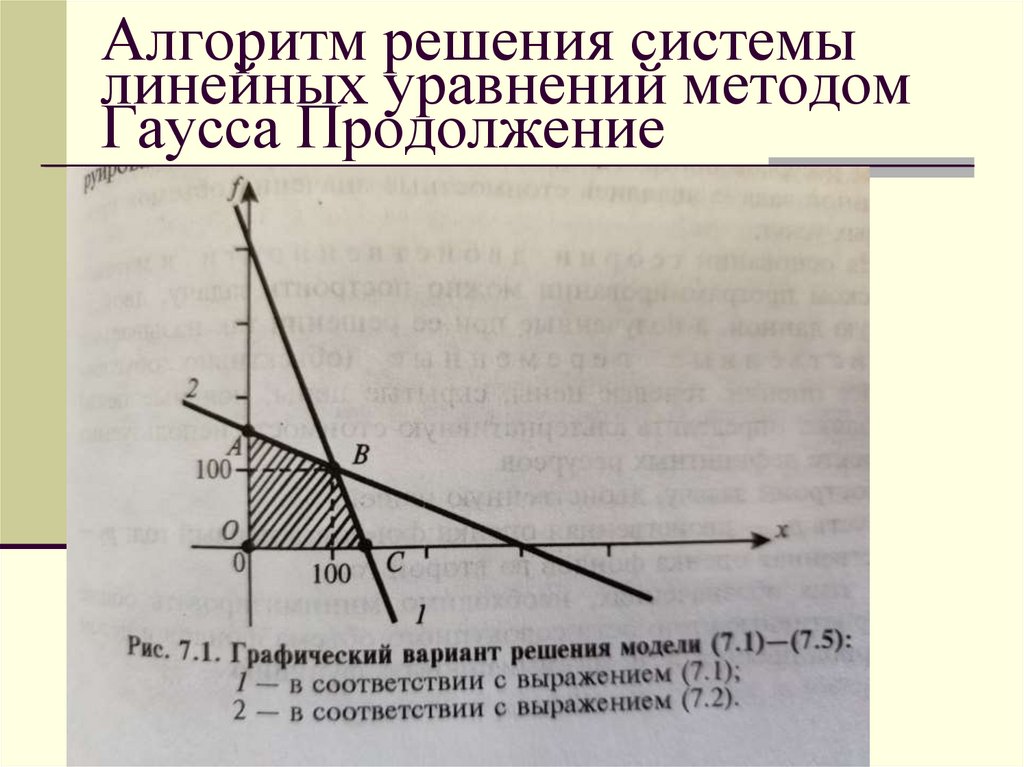
100f+300x<=40000
200f+100x<=30000
Целевая функция
400f+500x
max
(Проверять четыре точки
0;0;
0; 150;
точка решения пары уравнений;
400/3; 0; )

12. Алгоритм решения системы линейных уравнений методом Гаусса Продолжение

13. Численныеметоды решения дифференциальных уравнений

Описать качественно процедуру численного
решения дифференциального уравнения и
пояснить, какие существуют принципиальные
трудности в построении численного алгоритма
решения дифференциального уравнения.

14.

Спасибо
за
внимание!
Иванов Александр Владимирович
[email protected]
14