Основы теории кодирования. Основные понятия

1.

Основы теории кодирования
Основные понятия

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.

32.

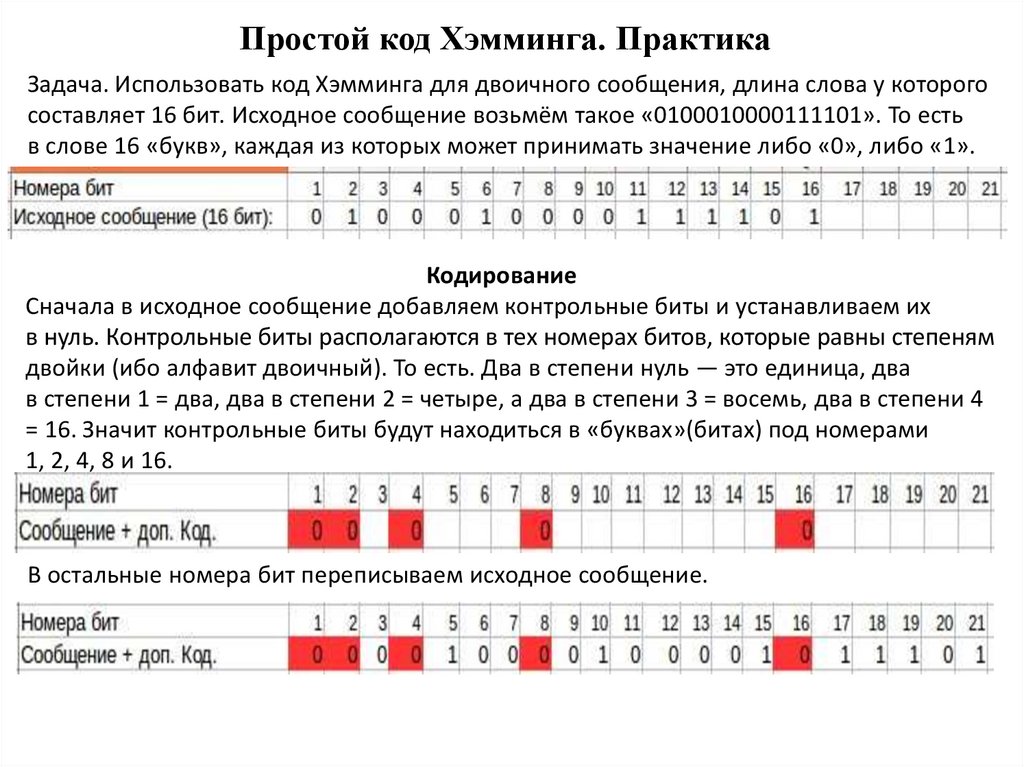
Простой код Хэмминга. Практика
Задача. Использовать код Хэмминга для двоичного сообщения, длина слова у которого
составляет 16 бит. Исходное сообщение возьмём такое «0100010000111101». То есть
в слове 16 «букв», каждая из которых может принимать значение либо «0», либо «1».
Кодирование
Сначала в исходное сообщение добавляем контрольные биты и устанавливаем их
в нуль. Контрольные биты располагаются в тех номерах битов, которые равны степеням
двойки (ибо алфавит двоичный). То есть. Два в степени нуль — это единица, два
в степени 1 = два, два в степени 2 = четыре, а два в степени 3 = восемь, два в степени 4
= 16. Значит контрольные биты будут находиться в «буквах»(битах) под номерами
1, 2, 4, 8 и 16.
В остальные номера бит переписываем исходное сообщение.

33.

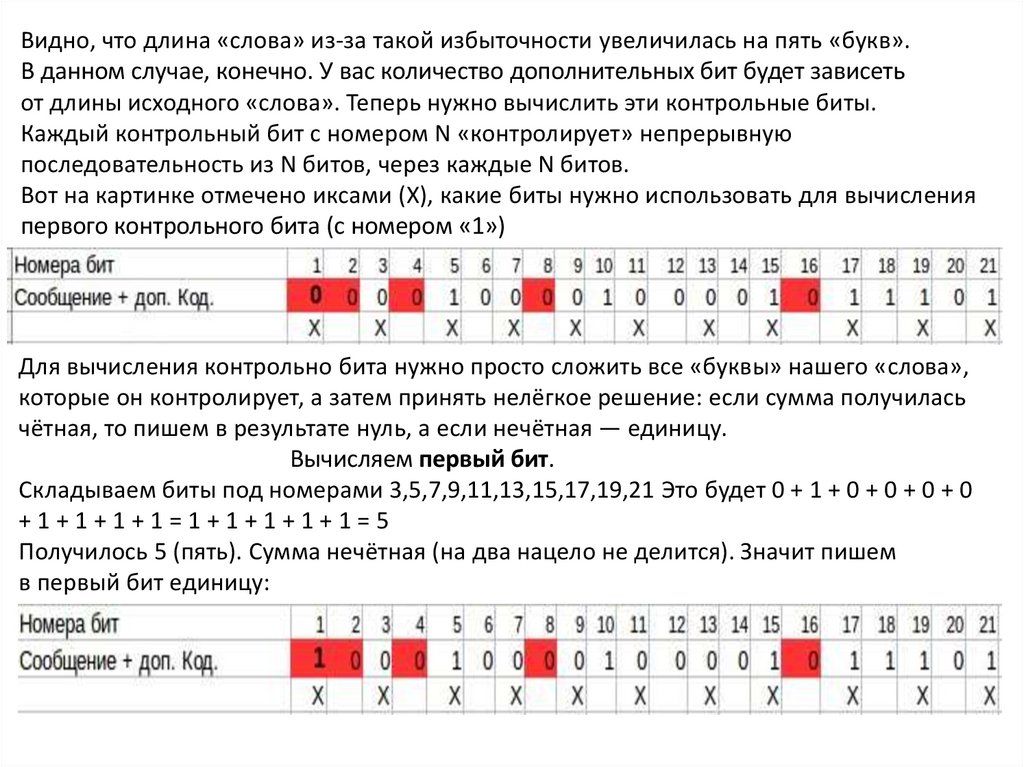
Видно, что длина «слова» из-за такой избыточности увеличилась на пять «букв».
В данном случае, конечно. У вас количество дополнительных бит будет зависеть
от длины исходного «слова». Теперь нужно вычислить эти контрольные биты.
Каждый контрольный бит с номером N «контролирует» непрерывную
последовательность из N битов, через каждые N битов.
Вот на картинке отмечено иксами (X), какие биты нужно использовать для вычисления
первого контрольного бита (с номером «1»)
Для вычисления контрольно бита нужно просто сложить все «буквы» нашего «слова»,
которые он контролирует, а затем принять нелёгкое решение: если сумма получилась
чётная, то пишем в результате нуль, а если нечётная — единицу.
Вычисляем первый бит.
Складываем биты под номерами 3,5,7,9,11,13,15,17,19,21 Это будет 0 + 1 + 0 + 0 + 0 + 0
+1+1+1+1=1+1+1+1+1=5
Получилось 5 (пять). Сумма нечётная (на два нацело не делится). Значит пишем
в первый бит единицу:

34.

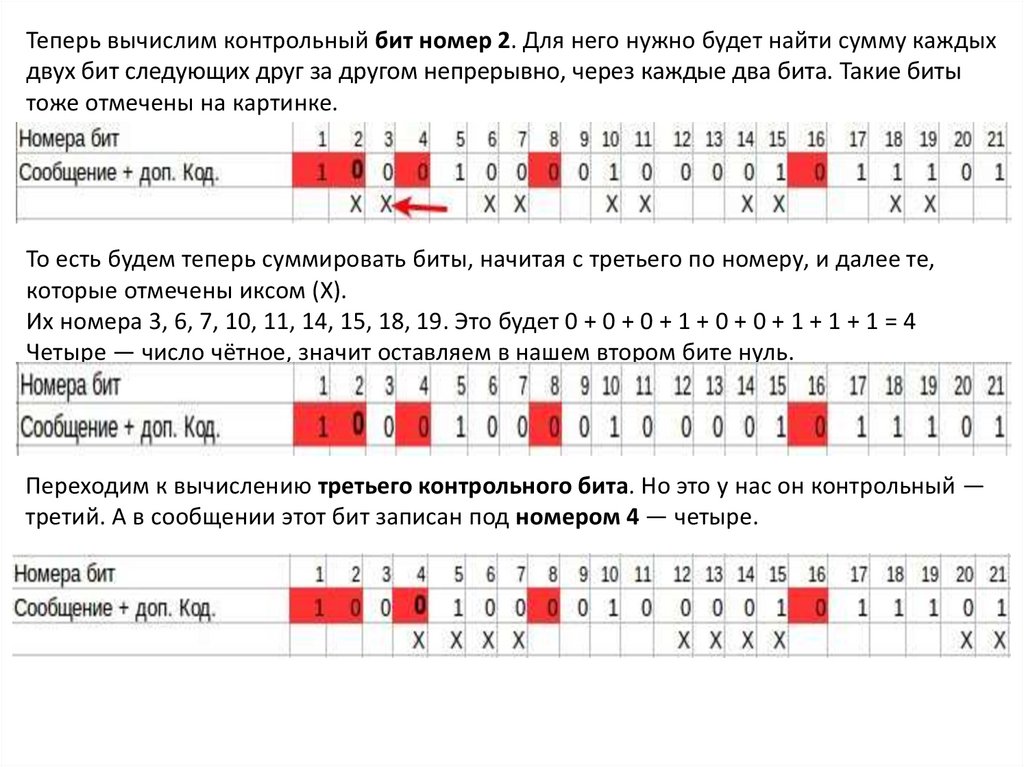
Теперь вычислим контрольный бит номер 2. Для него нужно будет найти сумму каждых
двух бит следующих друг за другом непрерывно, через каждые два бита. Такие биты
тоже отмечены на картинке.
То есть будем теперь суммировать биты, начитая с третьего по номеру, и далее те,
которые отмечены иксом (X).
Их номера 3, 6, 7, 10, 11, 14, 15, 18, 19. Это будет 0 + 0 + 0 + 1 + 0 + 0 + 1 + 1 + 1 = 4
Четыре — число чётное, значит оставляем в нашем втором бите нуль.
Переходим к вычислению третьего контрольного бита. Но это у нас он контрольный —
третий. А в сообщении этот бит записан под номером 4 — четыре.

35.

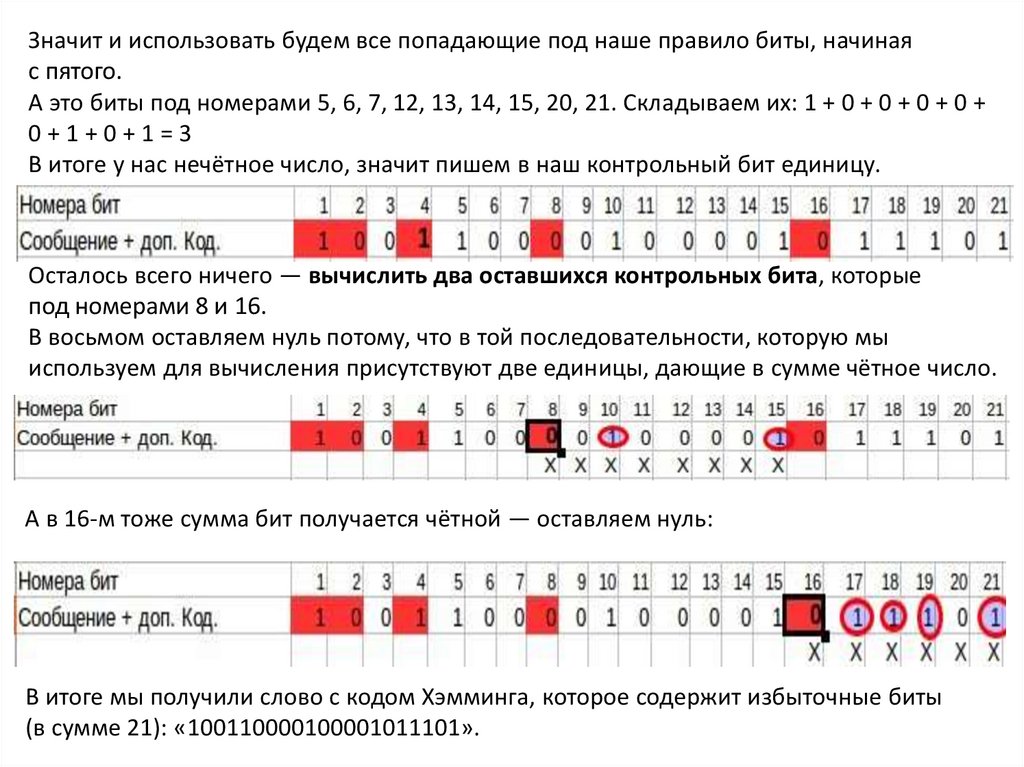
Значит и использовать будем все попадающие под наше правило биты, начиная
с пятого.
А это биты под номерами 5, 6, 7, 12, 13, 14, 15, 20, 21. Складываем их: 1 + 0 + 0 + 0 + 0 +
0+1+0+1=3
В итоге у нас нечётное число, значит пишем в наш контрольный бит единицу.
Осталось всего ничего — вычислить два оставшихся контрольных бита, которые
под номерами 8 и 16.
В восьмом оставляем нуль потому, что в той последовательности, которую мы
используем для вычисления присутствуют две единицы, дающие в сумме чётное число.
А в 16-м тоже сумма бит получается чётной — оставляем нуль:
В итоге мы получили слово с кодом Хэмминга, которое содержит избыточные биты
(в сумме 21): «100110000100001011101».

36.

Декодирование
А теперь представим, что к нам пришло сообщение с ошибкой. Вот оно
«100110001100001011101».
Мы знаем, что в него добавлены избыточные биты по алгоритму Хемминга, и нам
надо проверить, есть в нём ошибка или нет.
Для этого нужно поступить следующим образом. Сначала вычисляем заново все
контрольные биты по предыдущему алгоритму.
Для этого сначала обнуляем все биты, находящиеся на номерах степеней двойки:
В первом оставляем нуль, ибо в подконтрольных битах чётное число единиц.
Вычисляем все остальные контрольные биты по описанному выше алгоритму (мне лень
заново его описывать тут), и получаем, что не совпадают контрольные биты
под номерами 1 и 8:

37.

Теперь складываем номера этих контрольных бит: 1 + 8, и получаем 9 — номер бита,
в котором закралась ошибка!
Теперь просто меняем девятый бит на обратный — с единицы на нуль, — и получаем
исходное сообщение!
Отметим, что это самый простейший алгоритм Хемминга, который может исправить
только одну ошибку в слове.