Методы исследования жёстких систем. Моделирование химической кинетики

1.

МЕТОДЫ ИССЛЕДОВАНИЯ ЖЁСТКИХ СИСТЕМ. МОДЕЛИРОВАНИЕ
ХИМИЧЕСКОЙ КИНЕТИКИ
Последовательное протекание некоторых химических реакций веществ
описывается системой дифференциальных уравнений
dc1
dt k1c1 k 23c3 c2 ,
dc2
k1c1 k 23c2 c3 k 2 c2 ,
dt
dc3
dt k 3 c2 .
(4.1)
Где с1, с2, с3 концентрации реагентов, k1, k2, k23, k3 коэффициенты равные
соответственно 0.1, 6.103, 102, 8.103. Диапазон изменения переменной от 0 до 50.
Начальные значения функций с1, с2, с3 соответственно равны 1, 0.001, 0.03.
Для данной задачи стандартным методом Рунге – Кутты не удаётся найти
решение даже при использовании очень большого количество шагов, N =
100000. В процессе работы алгоритма решение расходится, и вместо результата
MathCAD выдаёт ошибку.
1

2.

Будем считать, что жёсткие системы – это те уравнения, решение которых
получить намного проще с помощью определённых специальных методов, чем
с помощью явных методов. Заметим, что одни и те же уравнения с разными
коэффициентами могут быть как жёсткими, так и нежёстким.
Символьный вектор правых частей системы ОДУ, описывающей динамику
концентрации реагентов, записывается
0.1 c1 102 c2 c3
2
3
F (t , c) : 0.1 c1 10 c2 c3 8 10 c2
6 103 c2
(4.2)
Бросается в глаза сильно различающийся порядок коэффициентов при
разных слагаемых. Именно степень этого различия чаще всего и определяет
жёсткость системы ОДУ. В качестве соответствующей характеристики выбирают
матрицу Якоби (якобиан) векторной функции F(t,c), т.е. функциональную
матрицу, составленную из производных F(t,c).
Для решения жёстких систем ОДУ в пакете MathCad имеются функции Stiffr
(vi, tmin, tmax, n, f, J) и Stiffb (vi, tmin, tmax, n, f, J), где vi- вектор начальных
значений, tmin- начальное значение переменной, tmах- конечное значение
переменной, n - число шагов, на которые разбит интервал tmах – tmin, f символьный вектор правых частей системы уравнений, J - матрица n n + 1,
первый столбец которой содержит производные по текущей переменной, а
остальные – якобиан системы ОДУ.
2

3.

Подробнее рассмотрим задание матричной функции J(t,c). Матричная
функция J(t,c) содержит столбец частных производных по t и якобиан. Так как
заданная система не содержит переменной t в явном виде, то первый столбец
матричной функции J(t,c) будет содержать нули.
Якобиан – матрица, составленная из частных производных векторной
функции по всем её аргументам.
3

4.

MathCad документ моделирования химической кинетики
коэффициенты
уравнения
начальные
значения
искомых
функций
вектор
правых
частей
системы
4

5.

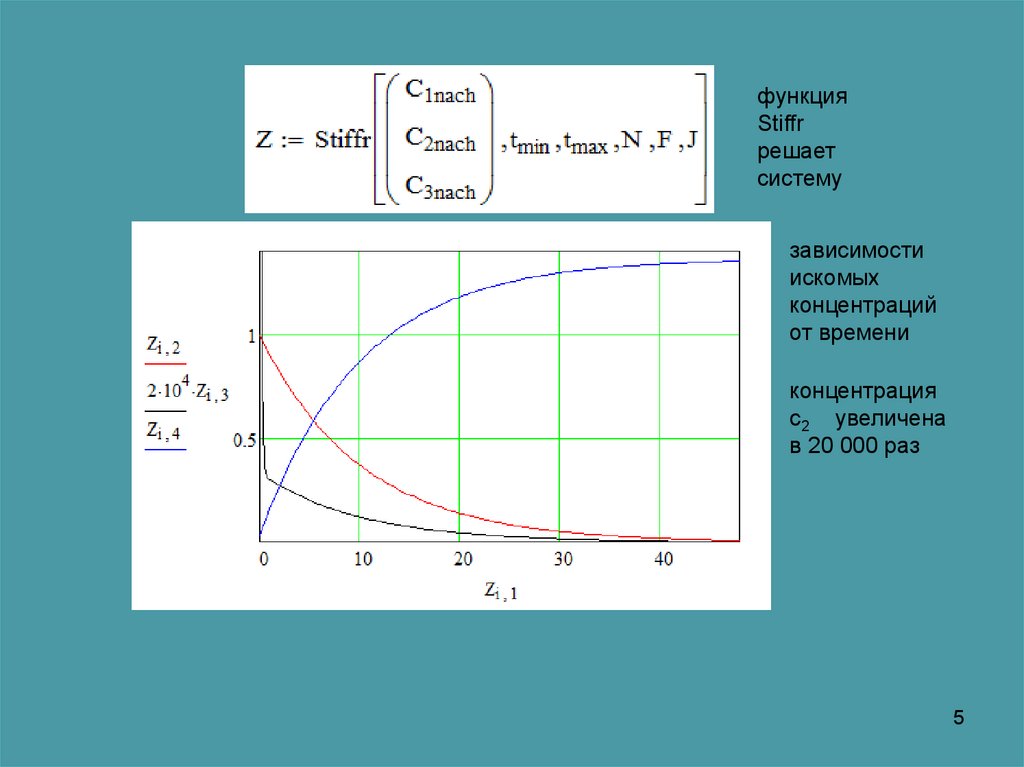
функция
Stiffr
решает
систему
зависимости
искомых
концентраций
от времени
концентрация
с2 увеличена
в 20 000 раз
5

6.

В 14-й версии MathCad добавились функции BDF(vi, tmin, tmax, n, f, [J],
[tol]), реализующая метод
BDF для решения жёстких систем ОДУ,
AdamsBDF(vi, tmin, tmax, n, f, [J], [tol]), - функция автоматически определяет,
является ли система ОДУ жёсткой и выбирает метод BDF или определяет,
что система ОДУ не является жёсткой и выбирает метод Адамса.
Получив решение, необходимо убедиться, что оно не является ошибочным,
а погрешности не превышают приемлемых значений.
6