Метод Promethee II в задачах многокритериального ранжирования

1.

Южный федеральный университет
Кафедра синергетики и процессов управления
Презентации к практическим занятиям
по дисциплине
«Теория систем и системный анализ»
тема:
«Метод PROMETHEE II в задачах
многокритериального ранжирования»

2.

Список использованных источников
1. Brans J.P., Vincke Ph. A PREFERENCE RANKING ORGANISATION METHOD (The
PROMETHEE Metod for Multiple Criteria Decision-Making) // Management science. – 1985. – Vol. 31.
– Р. 647–656.
2. Brans J.P., Vincke Ph., Mareschal B. How to select and how to rank projects: The PROMETHEE
method // European Journal of Operational Research. –1986. – Vol. 24. – P. 228–238.
3. Brans J.P., Mareschal B. PROMETHEE METHODS. Multiple Criteria Decision Analysis: State of the
Art Surveys. –2005. – P. 163–196.
4. Behzadian M., Kazemzadeh R.B., Albadvi A., Aghdasi M. PROMETHEE: A comprehensive literature
review on methodologies and applications // European Journal of Operational Research. –2000. – Vol.
200. – P. 198–215.
5. Macharis C., Springael J., Klaas De Brucker, Verbeke A. PROMETHEE and AHP: The design of
operational synergies in multicriteria analysis. Strengthening PROMETHEE with ideas of AHP //
European Journal of Operational Research. –2004. – Vol. 153. – P. 307–317.
6. Abedi M., Ali Torabi S., Norouzi G., Hamzeh M., Elyasi G. PROMETHEE II: A knowledge-driven
method for copper exploration // Computers & Geosciences. –2012. – Vol. 46. – P. 255–263.
7. Deshmukh S.C. Preference Ranking Organization Method Of Enrichment Evaluation
(PROMETHEE) // International Journal of Engineering Science Invention. –2013. – Vol. 2. – P. 28–34.
8. Tong, L., Pu, Z., Chen, K., Yi, J. Sustainable maintenance supplier performance evaluation based on
an extend fuzzy PROMETHEE II approach in petrochemical industry // Journal of Cleaner Production.
–2020. – Vol. 273. – A. 122771.
9. De Smet Y., Lidouh K. An Introduction to Multicriteria Decision Aid: The PROMETHEE and GAIA
Methods // European Business Intelligence Summer Shool. –2012. – Vol. 138. – P. 150–176.
2

3.

Введение
Метод многокритериального оценивания PROMETHEE был впервые
предложен Жан-Пьером Брансом (J.-P. Brans) в 1982 году на конференции в
университете Лаваля (Канада). Расшифровывается как Preference Ranking
Organization METHod for Enrichment Evaluation – «Метод формирования
рангов предпочтения для обогащения оценок»
PROMETHEE – это метод как ранжирования, так и выбора наилучшего
решения из множества альтернатив с учетом ряда конфликтующих критериев.
Существуют версии PROMETHEE I, II и др. Отличие методов I и II
заключается в том, что результатом метода PROMETHEE I является
частичное ранжирование альтернатив (есть несравнимые), а PROMETHEE II
позволяет ЛПР найти полный ранжированный вектор альтернатив (т. е.
построить полное ранжирование, в котором между всеми альтернативами есть
какое-то бинарное отношение – предпочтительности или безразличия).
3

4.

В основу метода PROMETHEE II положено попарное сравнение альтернатив по
каждому критерию в отдельности.
Альтернативы оцениваются в соответствии с различными по направлению
критериями, которые могут изначально как максимизироваться, так и
минимизироваться,
поэтому
учет
направления
осуществляется
выбором
соответствующей аналитической формы стандартной функции предпочтения. При
оценке альтернатив критерии могут быть как качественными, так и количественными.
Оценки по качественным критериям для расчетов методом PROMETHEE II
целесообразно перевести в балльную или ранговую шкалу.
Входными данными для метода PROMETHEE II является множество из n решений
(альтернатив) Х={Ai, i=1,…, n}, имеющих оценки uij по m критериям F={fj, j=1,…, m}
в форме матрицы полезностей (решений).
От ЛПР также требуется следующая априорная информация:
задать веса важности критериев;
выбрать для каждого критерия функцию предпочтений с соответствующими ей
параметрами.
4

5.

1. Алгоритм метода PROMETHEE II
Шаг 1. Задание весов важности критериев и выбор функций предпочтения
для каждого критерия.
В методе PROMETHEE II предполагается, что ЛПР способно надлежащим
образом взвесить критерии по важности – назначить веса важности.
Вес важности j-го критерия wj является входными данными, т.е. должен
быть предварительно определен, при этом в рассматриваемом ниже
m
алгоритме обязательно должно выполняться условие нормировки w j 1 .
j 1
5

6.

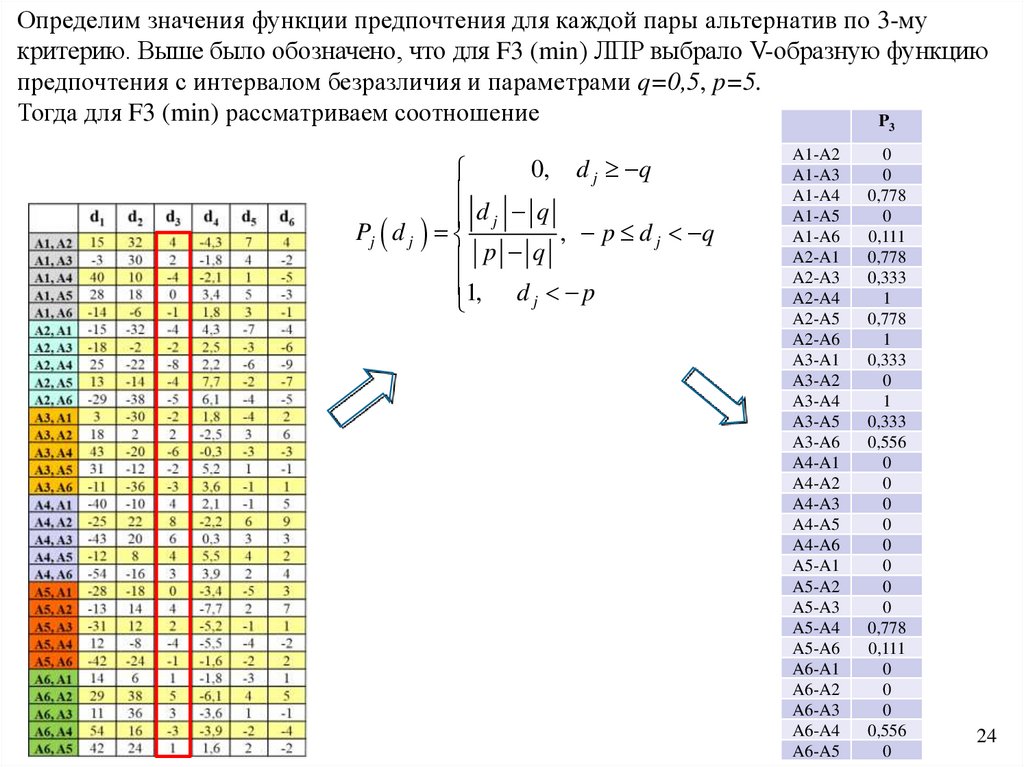
Функция предпочтения Pj(a, b) – это функция, выражающая интенсивность
предпочтения альтернативы a по отношению к альтернативе b по критерию j, т. е. для
каждого критерия функция предпочтения преобразует разницу dj = (a, b) между
оценками двух альтернатив по данному критерию в степень предпочтения,
изменяющуюся от нуля до единицы: Pj(a, b) = Pj(dj ) [0, 1].
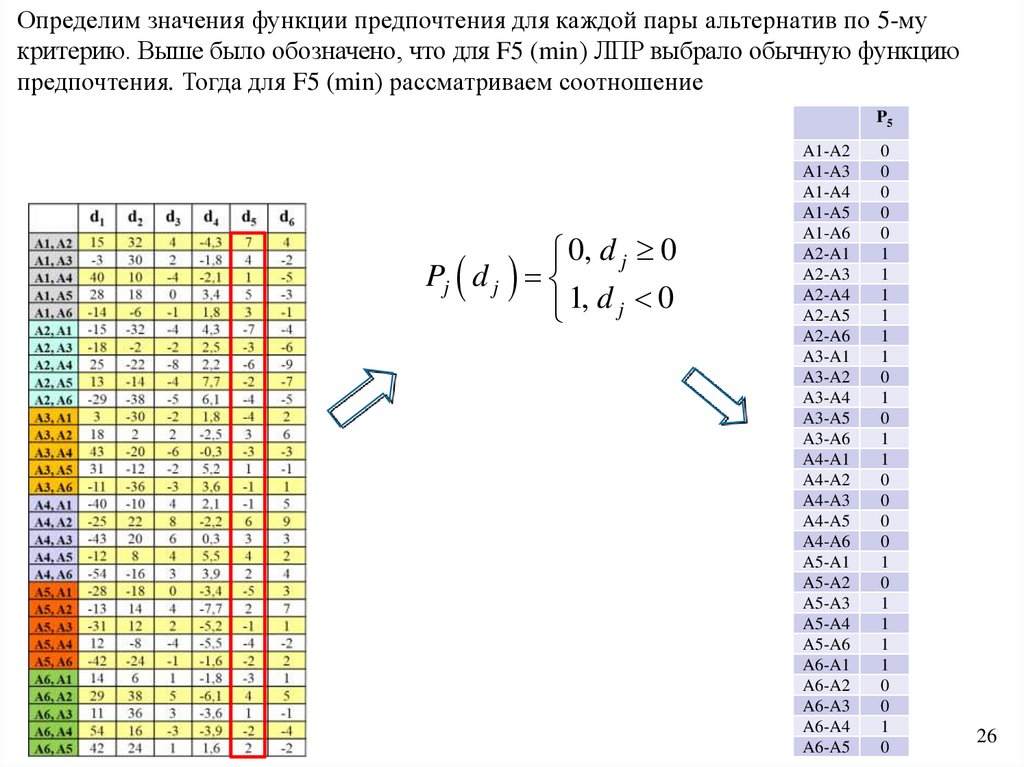
Pj(a, b) = 0 – означает безразличие (indifference), отсутствие предпочтения
альтернативы a по отношению к альтернативе b;
Pj(a, b) 0 – означает слабое (weak) предпочтение альтернативы a по
отношению к альтернативе b;
Pj(a, b) 1 – означает сильное (strong) предпочтение альтернативы a по
отношению к альтернативе b;
Pj(a, b) = 1 – означает строгое (strict) предпочтение альтернативы a по
отношению к альтернативе b.
6

7.

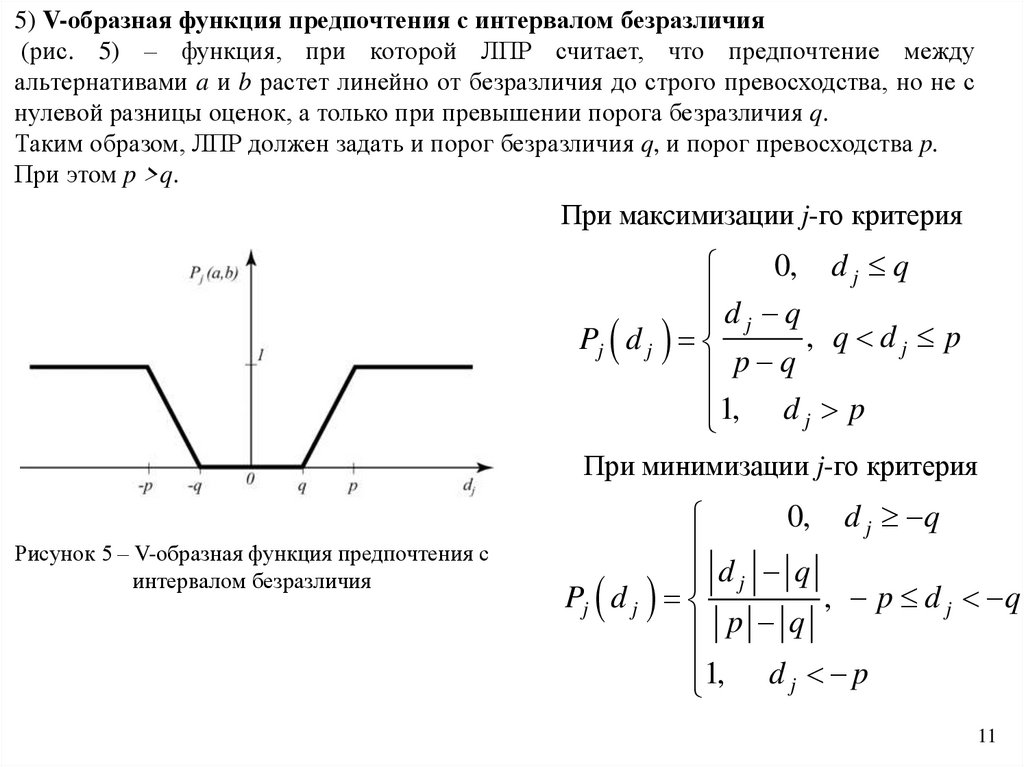
Выделяют шесть типовых функций предпочтения [2]:
1) Обычная функция предпочтения (рис. 1) – это функция, при которой существует
безразличие между альтернативами a и b только, если