Метод имитационного моделирования. Единичный жребий и формы его организации. Примеры задач

1.

Метод имитационного
моделирования. Единичный
жребий и формы его организации.
Примеры задач

2.

Имитационное моделирование
• Имитационное моделирование (ИМ) – распространённая
разновидность аналогов моделирования, реализуемого с
помощью набора математических инструментальных средств,
специальных имитирующих программных средств и технологий
программирования, позволяющих посредствам процессов
аналогов провести целенаправленное исследование структуры
и функций реального сложного процесса в памяти компьютера
в режиме «имитации», выполнить оптимизацию некоторых его
параметров. Имитационной моделью (ИМ) называется
специальный программный комплекс, позволяющий
имитировать деятельность какого-либо сложного объекта. Он
выполняет на компьютере параллельно взаимодействующие
процессы, которые являются по своим временным параметрам
(с точностью по масштабам времени и пространства) аналогами
исследуемых процессов.

3.

ИМ
• ИМ удобно для исследования практических задач: определение
показателей эффективности, сравнение вариантов построения и
алгоритмов функционирования систем, проверки устойчивости
режимов системы при малых отклонениях входных
переменных от расчётных значений. Полнота имитации может
быть проверена путём построения серии последовательно
уточняемых моделей. Если дальнейшая детализация свойств
модели не влияет на конечные показатели, то усложнение
модели можно прекратить. Как правило, моделируются те
свойства процесса, которые могут влиять на выбранный
показатель эффективности или критичны к наложенным
ограничениям. Промежуточные результаты имитационного
моделирования имеют четкий физический смысл и позволяют
обнаружить ошибки программы.

4.

Недостатки
ИМ присущи и недостатки:
• большой расход машинного времени;
• малая точность вероятностных характеристик
редких событий;
• трудность получения обобщающих выводов и
рекомендаций;
• сложность оптимизации системы
(многовариантность расчётов при наличии
вероятностных помех);
• вероятностная оценка погрешности

5.

Таким образом применение ИМ становится
целесообразным:
• для накопления первичных данных об
изучаемом явлении, если эти данные нельзя
получить в натурном эксперименте;
• для проверки планомерности допущений,
сделанных разработчиком в целях перехода к
аналитическим методам,
• для демонстрации конечных результатов
исследования на достаточно полной модели
реальной ситуации,
• при «безысходности», когда сложность ситуации
намного превосходит возможности
аналитических методов, известных
разработчику.

6.

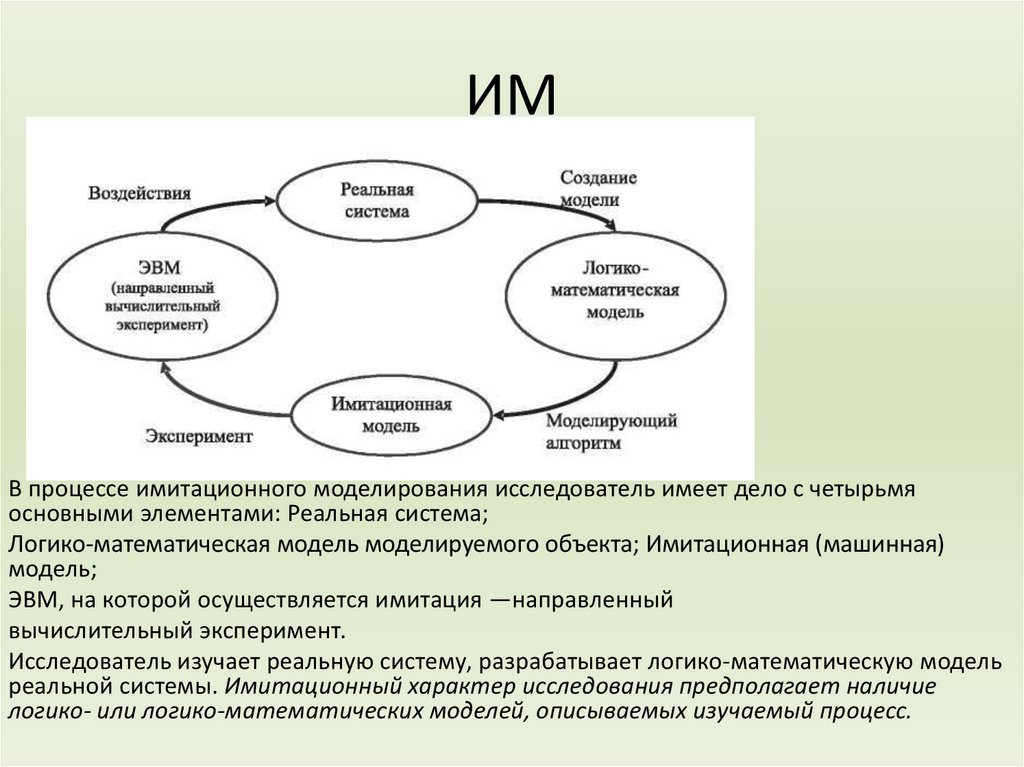
ИМ
В процессе имитационного моделирования исследователь имеет дело с четырьмя
основными элементами: Реальная система;
Логико-математическая модель моделируемого объекта; Имитационная (машинная)
модель;
ЭВМ, на которой осуществляется имитация —направленный
вычислительный эксперимент.
Исследователь изучает реальную систему, разрабатывает логико-математическую модель
реальной системы. Имитационный характер исследования предполагает наличие
логико- или логико-математических моделей, описываемых изучаемый процесс.

7.

ИМ
При имитационном моделировании структура моделируемой
системы адекватно отображается в модели, а процессы ее
функционирования проигрываются (имитируются) на построенной
модели. Поэтому построение имитационной модели заключается
в описании структуры и процессов функционирования
моделируемого объекта или системы. В описании имитационной
модели выделяют две составляющие:
• Статическое описание системы, которое по-существу
является описанием ее структуры. При разработке
имитационной модели необходимо выполнять структурный
анализ моделируемых процессов.
• Динамическое описание системы, или описание динамики
взаимодействий ее элементов. При его составлении фактически
требуется построение функциональной модели моделируемых
динамических процессов.

8.

ИМ
Отличительной особенностью метода имитационного
моделирования является возможность описания и
воспроизведения взаимодействия между различными
элементами системы. Таким образом, чтобы составить
имитационную модель, надо:
• представить реальную систему (процесс), как
совокупность
• взаимодействующих элементов;
• алгоритмически описать функционирование отдельных
элементов;
• описать процесс взаимодействия различных элементов
между собой и
• с внешней средой.

9.

ИМ
• Ключевым моментом в имитационном моделировании
является выделение и описание состояний системы. Система
характеризуется набором переменных состояний, каждая
комбинация которых описывает конкретное состояние.
Следовательно, путем изменения значений этих переменных
можно имитировать переход системы из одного состояния в
другое. Таким образом, имитационное моделирование -это
представление динамического поведения системы посредством
продвижения ее от одного состояния к другому в соответствии с
хорошо определенными операционными правилами. Эти
изменения состояний могут происходить либо непрерывно,
либо в дискретные моменты времени. Имитационное
моделирование -есть динамическое отражение изменений
состояния системы с течением времени.

10.

Основные функции ИМ
• Для создания ИМ необходима специальная
система моделирования, имеющая набор
языковых средств, сервисные
подпрограммы, приёмы и технологии
программирования. ИМ должна отражать
большое число параметров, логику и
закономерности поведения моделируемого
объекта во времени (временная динамика),
а для объектов экономики существует
понятие финансовой динамики.

11.

Основные функции ИМ
ИМ контролируемого объекта или процесса обеспечивается двумя
видами деятельности, выполняемыми с помощью компьютера:
• работа по созданию или модификации ИМ;
• эксплуатация ИМ и интерпретация результатов
ИМ систем применяется в двух случаях:
• для управления сложным процессом, когда ИМ управляемого
объекта используется в качестве инструментального средства в
контуре адаптивной системы управления, создаваемой на
основе имитационных технологий;
• при проведении экспериментов с дискретно-непрерывными
моделями сложных объектов для получения и отслеживания их
динамики в экстренных ситуациях, связанными с рисками,
натурное моделирование которых нежелательно или
невозможно.

12.

Единичный жребий и формы его
организации.
• Основным элементом, из совокупности которых
складывается монте-карловская модель, является одна
случайная реализация моделируемого явления,
например: один «обстрел» цели, один «день работы»
транспорта, одна «эпидемия» и т. п.
• Реализация представляет собой как бы один случай
осуществления моделируемого случайного явления
(процесса) со всеми присущими ему случайностями.
Она разыгрывается с помощью специально
разработанной процедуры или алгоритма, в котором
важную роль играет собственно «розыгрыш» или
«бросание жребия». Каждый раз, когда в ход
моделируемого процесса вмешивается случайность, ее
влияние учитывается не расчетом, а бросанием жребия.

13.

Единичный жребий
• Предположим, что в ходе моделируемого процесса наступил
момент, когда его дальнейшее развитие (а значит, и результат)
зависит от того, появилось ли на данном этапе событие А или
не появилось? Например: произошло ли попадание в цель?
Обнаружен ли некоторый объект? Исправна ли аппаратура?
Появилась ли заявка на обслуживание? и т. д.
• Тогда нужно «бросанием жребия» решить вопрос: появилось
событие А или не появилось? Для этого нужно привести в
действие некоторый случайный механизм розыгрыша (скажем,
бросить игральную кость, или несколько монет, или выбрать
число из таблицы случайных чисел) и условиться о том, какой
результат жребия означает появление, а какой — непоявление
события А. Ниже мы увидим, что розыгрыш всегда может быть
организован так, чтобы событие А имело любую наперед
заданную вероятность.

14.

Единичный жребий
• Тогда нужно «бросанием жребия» решить вопрос: появилось
событие А или не появилось? Для этого нужно привести в
действие некоторый случайный механизм розыгрыша (скажем,
бросить игральную кость, или несколько монет, или выбрать
число из таблицы случайных чисел) и условиться о том, какой
результат жребия означает появление, а какой — непоявление
события А. Ниже мы увидим, что розыгрыш всегда может быть
организован так, чтобы событие А имело любую наперед
заданную вероятность.
• Кроме событий, появляющихся случайным образом, на ход и
исход операции могут также влиять разные случайные величины
(например, время обслуживания заявки каналом СМО;
координаты точки попадания снаряда; время, в течение которого
выполняется рейс автомашины; число вышедших из строя узлов и
т. д.). С помощью жребия можно разыграть значение любой
случайной величины или совокупность значений нескольких
случайных величин.

15.

Единичный жребий
Условимся называть единичным жребием любой элементарный
опыт, в котором решается один из вопросов:
1. Произошло или не произошло событие А?
2. Какое из возможных событий А1,А2,…, Аk произошло?
3. Какое значение приняла случайная величина X?
4. Какую совокупность значений приняла система случайных
величин X1, Х2,…, Xk?
Каждая реализация случайного явления методом Монте-Карло
состоит из цепочки единичных жребиев, перемежающихся
обычными расчетами. Расчетами учитывается влияние исхода
единичного жребия на ход операции (в частности, на условия, в
которых будет осуществляться следующий единичный жребий).

16.

Единичный жребий
• Рассмотрим способы организации всех разновидностей
единичного жребия. Как уже было сказано выше, при любой
организации единичного жребия должен быть пущен в ход
какой-то механизм случайного выбора (бросание монет, костей,
вынимание жетона из вращающегося барабана, числа из
набора чисел, и т. д.). Такие механизмы могут быть самыми
разнообразными, однако любой из них может быть заменен
стандартным механизмом, позволяющим решить однуединственную задачу: получить случайную величину,
распределенную с постоянной плотностью от 0
до 1. Условимся для краткости называть такую случайную
величину «случайное число от 0 до 1» и обозначать R (от
английского random — случайный).
• Покажем, что любая задача единичного жребия может быть
решена с помощью стандартного механизма, дающего число R.

17.

Появилось или нет событие а?
Пусть вероятность
события А равна р:
Р(А) = р.
Выберем с помощью
стандартного механизма
случайное число R и будем
считать, что если оно
меньше р, событие А произошл
о, если больше р — не
произошло (получение R, в
точности равного р, будем
считать практически
невозможным).
Действительно, если R —
случайное число от 0 до 1, то

18.

Какое из нескольких возможных
событий появилось?
Пусть имеется полная группа
несовместных событий:
А1, A2,,…, Аk
с вероятностями
p1 ,р2,, …, рk.
• Так как события несовместны и
образуют полную группу, то
Разделим весь интервал от 0 до 1
на k участков длиной p1 ,р2,, …,
рk .(рис. 8.2). Если случайное
число R, выданное стандартным
механизмом, попало, например,
на участок p3, это означает, что
появилось событие A3.

19.

Пример
Летательный аппарат, совершающий
полет над территорией противника,
после стрельбы по нему может
оказаться в одном из следующих
состояний:
А1 — невредим, продолжает полет;
А2 — поврежден, продолжает полет;
А3 —совершил вынужденную
посадку;
А4 — сбит.
Вероятности этих четырех событий
заданы: р1 = Р(А1) = 0,4; р2 = Р(А2) =
0,1; р3 = Р(А3) = 0,15; р4 = Р(А4) = 0,35.
Построить процедуру единичного
жребия для розыгрыша результата
обстрела.
• Решение. Делим участок (0, 1)
на четыре части, как показано
на рисунке.
• При попадании случайного
числа R на участок от 0 до 0,4
считать, что произошло
событие А1, на участок от 0,4 до
0,5 — событие А2 и т. д.

20.

Пример
Находим функцию распределения:
.
График функции распределения имеет вид:
Построить процедуру розыгрыша
значения случайной величины X,
плотность распределения которой
при
Там же показана процедура розыгрыша
значения случайной величины X.
Аналитически это выражается так:
откуда обратная функция
Х =агс sin (2R - 1).
Таким образом, для розыгрыша значения
случайной величины X нужно: взять
случайное число от 0 до 1, удвоить его,
вычесть единицу и от результата взять
арксинус.

21.

Спасибо!)