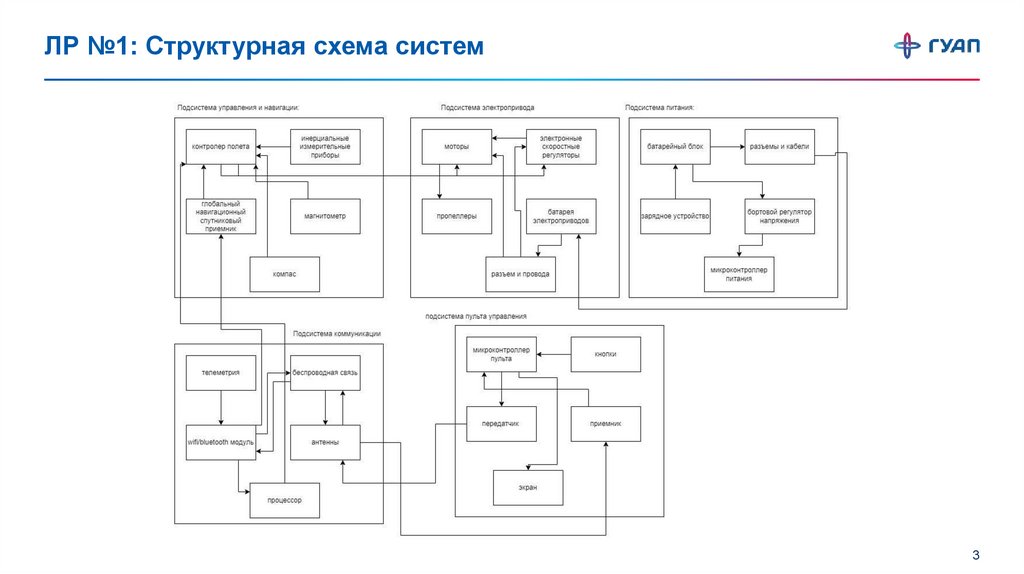
Квадрокоптер. Структурная схема систем

1.

Квадрокоптер
Д. А. Колесниченко, Д. В. Бадьин,
К. И. Стулов, М. А. Рахилов

2.

Вступление
Квадрокоптеры - сложные динамические
системы,
представляющие
собой
идеальный объект для моделирования.
Для нашего проекта по моделированию мы
выбрали именно данную тему из-за его
сложности и перспективных разработок.
Моделирование квадрокоптеров позволяет
изучать и оптимизировать поведение
сложных систем, открывая путь для более
совершенных и автономных беспилотных
летательных аппаратов.
2

3.

ЛР №1: Структурная схема систем
3

4.

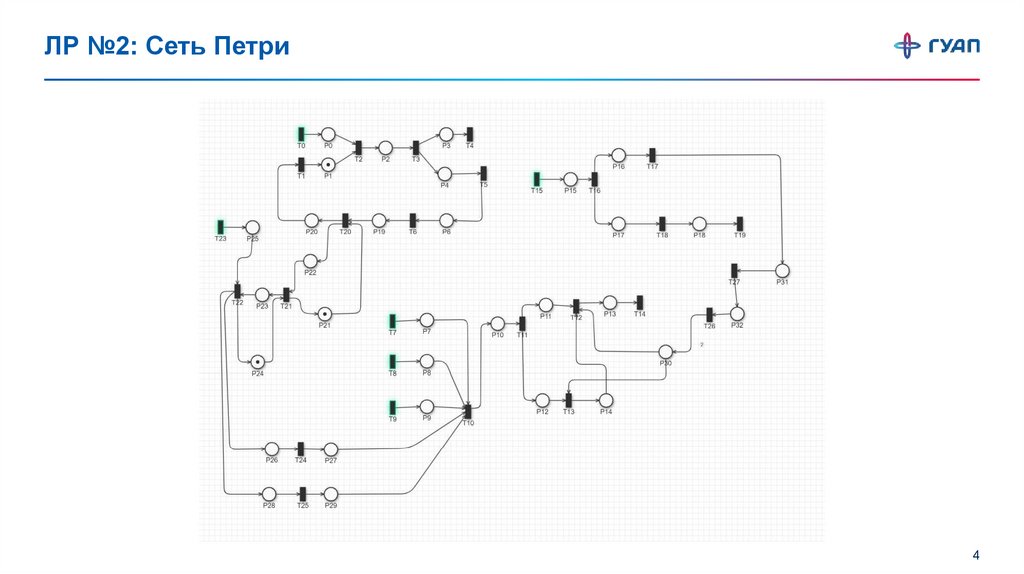
ЛР №2: Сеть Петри
4

5.

ЛР №3: Результаты анализа сети Петри
Безопасность: Данная сеть Петри не
является безопасной, поскольку число
фишек в ней может превышать единицу.
Ограниченность: Данная сеть Петри
неограниченная, поскольку число фишек в
некоторых
позициях
может
быть
бесконечным.
Сохранение: Сеть Петри не является
сохраняющей, поскольку общее число
фишек в сети постоянно меняется.
Активность: Сеть Петри активна, поскольку
в ней нет тупиков.
5

6.

ЛР №4: Матрица инцидентности и проверка маркировок
t0
p0
p1
p2
p3
p4
p5
p6
p7
p8
p9
p1
0
p1
1
p1
2
p1
3
p1
4
p1
5
p1
6
p1
7
p1
8
p1
9
p2
0
p2
1
p2
2
p2
3
p2
4
p2
5
p2
6
p2
7
p2
8
p2
9
p3
0
p3
1
p3
2
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
t1
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-1
0
0
0
0
0
0
0
0
0
0
0
0
t2
-1
-1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
t3
0
0
-1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
t4
0
0
0
-1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
t5
0
0
0
0
-1
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
t6
0
0
0
0
0
0
-1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
t7
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
t8
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
t9
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
t10
0
0
0
0
0
0
0
-1
-1
-1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-1
0
-1
0
0
0
t11
0
0
0
0
0
0
0
0
0
0
-1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
t12
0
0
0
0
0
0
0
0
0
0
0
-1
0
1
-1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-1
0
0
t13
0
0
0
0
0
0
0
0
0
0
0
0
-1
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-1
0
0
t14
0
0
0
0
0
0
0
0
0
0
0
0
0
-1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
t15
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
t16
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
t17
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
t18
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
t19
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
t20
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-1
1
-1
1
0
0
0
0
0
0
0
0
0
0
t21
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
-1
1
-1
0
0
0
0
0
0
0
0
t22
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-1
1
-1
1
0
1
0
0
0
0
t23
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
t24
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-1
1
0
0
0
0
0
t25
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-1
1
0
0
0
t26
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2
0
-1
t27
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-1
1
1.
Из первой ветви дерева была взята маркировка µa =
{0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,0}.
Вектор последовательностей запусков для нее x =
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1].
Тогда,
посчитав маркировку µ’ по формуле
µ’ = µ0 + x*D, находим,
что µ’ = µa.
2.
Из второй ветви дерева была взята маркировка µb =
{0,1,0,0,0,0,0,0,0,0,0,2,2,0,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,0,1,1}.
Вектор последовательностей запусков для нее x =
[2,2,2,2,2,2,2,2,2,2,2,2,0,0,0,2,2,2,2,2,2,2,2,2,2,2,0,1].
Тогда,
посчитав маркировку µ’ по формуле
µ’ = µ0 + x*D, находим,
что µ’ = µb.
3.
Из третьей ветви дерева была взята маркировка µс =
{0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,w,0,0,0,1,0,0,1,0,0,0,0,0,w,0,0}.
Вектор последовательностей запусков для нее x =
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,3,3,3,0,0,0,0,0,0,0,0,3,3].
Тогда,
посчитав маркировку µ’ по формуле
µ’ = µ0 + x*D, находим,
что µ’ = µс.
6