Приближенный алгоритм решения нелинейной задачи управления с фазовыми ограничениями

1. Приближенный алгоритм решения нелинейной задачи управления с фазовыми ограничениями

Курсовая работа
Приближенный алгоритм
решения нелинейной задачи
управления с фазовыми
ограничениями
Работу выполнил студент группы МП-201 Cараев С.О.
Научный руководитель
Изместьев Игорь Вячеславович
Должность доцент
Ученая степень канд. физ.-мат. наук
Челябинск 2023
Ученое звание доцент

2. Введение

Задачи курсовой работы:
Изучить научную литературу о методах решения нелинейных
задачу правления.
Разработать приближенный алгоритм решения нелинейной
задачи управления с фазовыми ограничениями.
Написать программу, которая реализует разработанный алгоритм
2

3. Описание метода Эйлера и его применение для численного решения дифференциальных уравнений

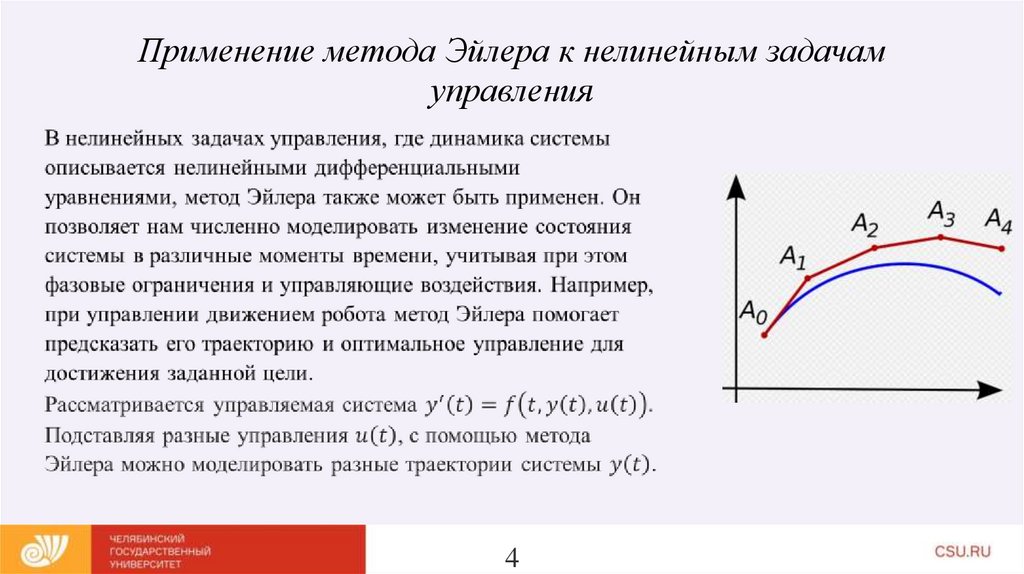
3

4. Применение метода Эйлера к нелинейным задачам управления

4

5. Описание предлагаемого приближенного алгоритма решения

5

6. Пример

6

7. Реализация приближенного алгоритма

7

8. Программная реализация приближенного алгоритма

код реализует численный метод
Эйлера для решения
дифференциального уравнения,
описывающего движение точки в
плоскости. Входные параметры
функции methodEuler включают
начальные условия (p0 - начальная
точка, t0 - начальное время), шаг
по времени tau, количество шагов
N, а также списки t и U,
содержащие значения времени и
управления соответственно.
8

9. Программная реализация приближенного алгоритма

Программа создает множество
траекторий, применяя метод
Эйлера для моделирования
движения точки. Затем выбирается
наилучшая траектория, вычисляя
расстояние от её конечной точки
до целевой точки. Если последняя
точка текущей траектории
оказывается ближе к цели, чем
последняя точка наилучшей
(согласно критерию качества)
траектории, то текущая траектория
сохраняется как новая наилучшая.
9

10. Заключение

В ходе исследования была изучена научная литературу о методах решения
нелинейных задачу правления.
Такая как:
Пантелеев А.В., Бортаковский А.С. Теория управления в примерах и задачах. М.: Высшая школа, 2003.
Беляев, А.И., Бреслав, Р.Б., Розов, Н.Х. "Теория управления." Москва: Наука,
1975.
Борисов, А.А., Моргунов, А.А. "Нелинейные динамические системы и их
управление." Санкт-Петербург: БХВ-Петербург, 2019.
Разработан приближенный алгоритм решения нелинейной задачи управления без
фазовых ограничений .
Написана программа, которая реализует разработанный алгоритм.
10