Комплексні частотні характеристики лінійних електричних кіл другого порядку

1.

ЛЕКЦІЯ 3.6
КОМПЛЕКСНІ ЧАСТОТНІ ХАРАКТЕРИСТИКИ
ЛІНІЙНИХ ЕЛЕКТРИЧНИХ КІЛ ДРУГОГО ПОРЯДКУ
поняття про коливальні кола;
послідовне коливальне коло;
паралельне коливальне коло

2.

Розглянемо лінійні електронні кола другого
порядку, до складу яких входить один
конденсатор та одна котушка індуктивності, які
з‘єднані послідовно або паралельно.
Такі кола називають коливальними колами.
Розрізняють послідовне та паралельне
коливальні кола.
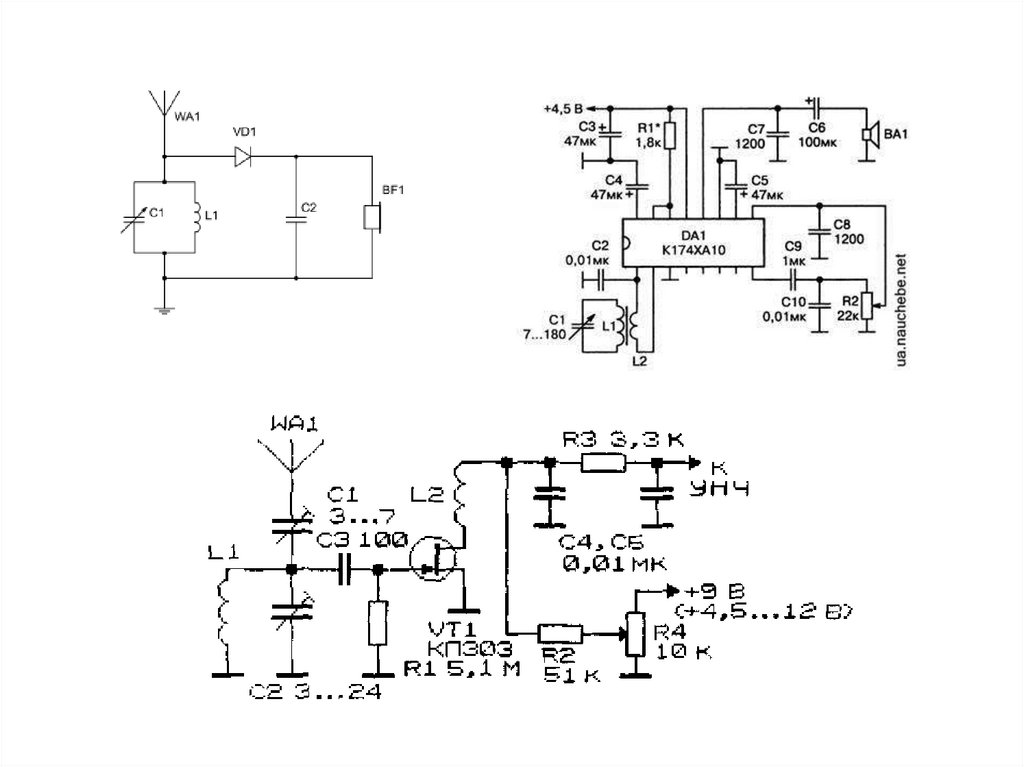
Їх широко використовують в різноманітних
радіотехнічних та телекомунікаційних пристроях:
приймачах, передавачах, генераторах сигналів
тощо.

3.

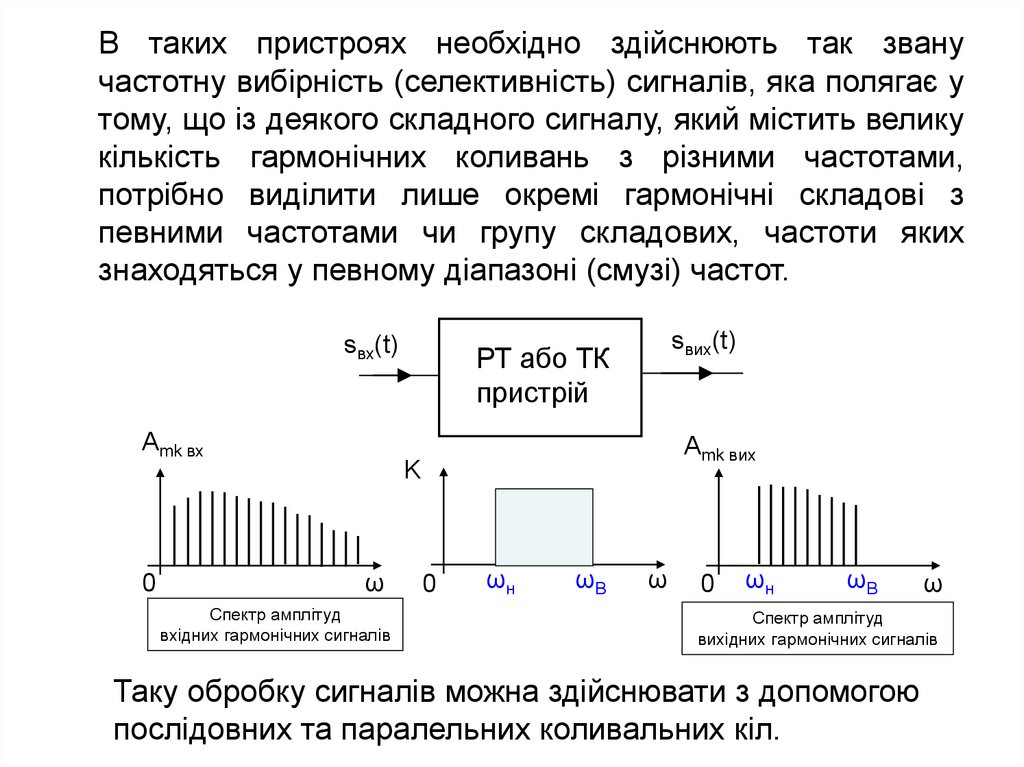
В таких пристроях необхідно здійснюють так звану
частотну вибірність (селективність) сигналів, яка полягає у
тому, що із деякого складного сигналу, який містить велику
кількість гармонічних коливань з різними частотами,
потрібно виділити лише окремі гармонічні складові з
певними частотами чи групу складових, частоти яких
знаходяться у певному діапазоні (смузі) частот.
sвх(t)
Amk вх
0
sвих(t)
РТ або ТК
пристрій
Amk вих
K
ω
Спектр амплітуд
вхідних гармонічних сигналів
0
ωн
ωВ
ω
0
ωн
ωВ
ω
Спектр амплітуд
вихідних гармонічних сигналів
Таку обробку сигналів можна здійснювати з допомогою
послідовних та паралельних коливальних кіл.

4.

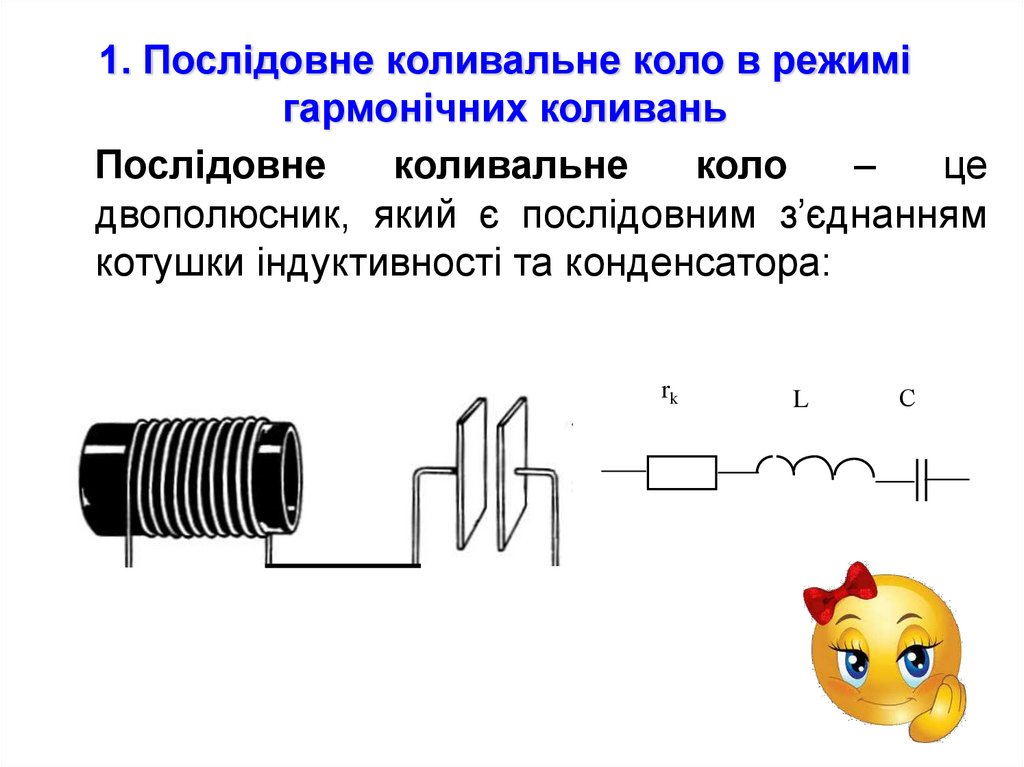
5. 1. Послідовне коливальне коло в режимі гармонічних коливань

Послідовне
коливальне
коло
–
це
двополюсник, який є послідовним з’єднанням
котушки індуктивності та конденсатора:
rk
L
С

6. Комплексний опір кола:

rk
L
С
Z = rk + jωL + 1/jωC = rk + j(ωL -1/ωC)=rk + jXk
Тут: rk - резистивна складова комплексного опору кола;
Хk=( L–1/ С) – реактивна складова комплексного опору
кола.
2
2 jarctg ( X K / rK )
Z
r
r
j
(
L
1
/
C
)
r
X
Z
ê
Показникова
форма
L
C запису:
K
Ke
На підставі алгебраїчної форми запису модуль та аргумент
комплексного опору будуть такими:
( L 1 / CZ)
/ rK ) -1/ωC)2
√rk2( X+K (ωL
rK2 X K2 e=jarctg
φ = arc tg(Xk/rk) = arc tg [(ωL -1/ωC)/rk].

7.

З отриманих виразів видно, що на деякій
частоті реактивна складова Хk стає рівною
нулеві, а модуль опору – мінімальним: Zk = rk.
Тобто комплексний опір кола стає активним
(резистивним), бо індуктивний та ємнісний опори
взаємно компенсуються.
Частота, на якій виникає це явище з рівняння:
ωL -1/ωC = 0
буде визначатись ємністю та індуктивністю:
1
ω = 0
рад / с
LC
або
f0
1
2 LC
Гц
Цю частоту називають резонансною частотою.

8.

Отже, на резонансній частоті абсолютні значення
реактивних опорів котушки та конденсатора рівні між
собою:
L
0 L 1 / 0 C
C
і при підстановці
0
1
рад / с
LC
можуть бути визначені через параметри компонентів кола:
L
0 L 1 / 0 C
C
L/C
Величину
називають характеристичним
опором коливального кола і позначають літерою ρ:
ρ = ωoL = 1/ωoC = √L/C , Ом

9.

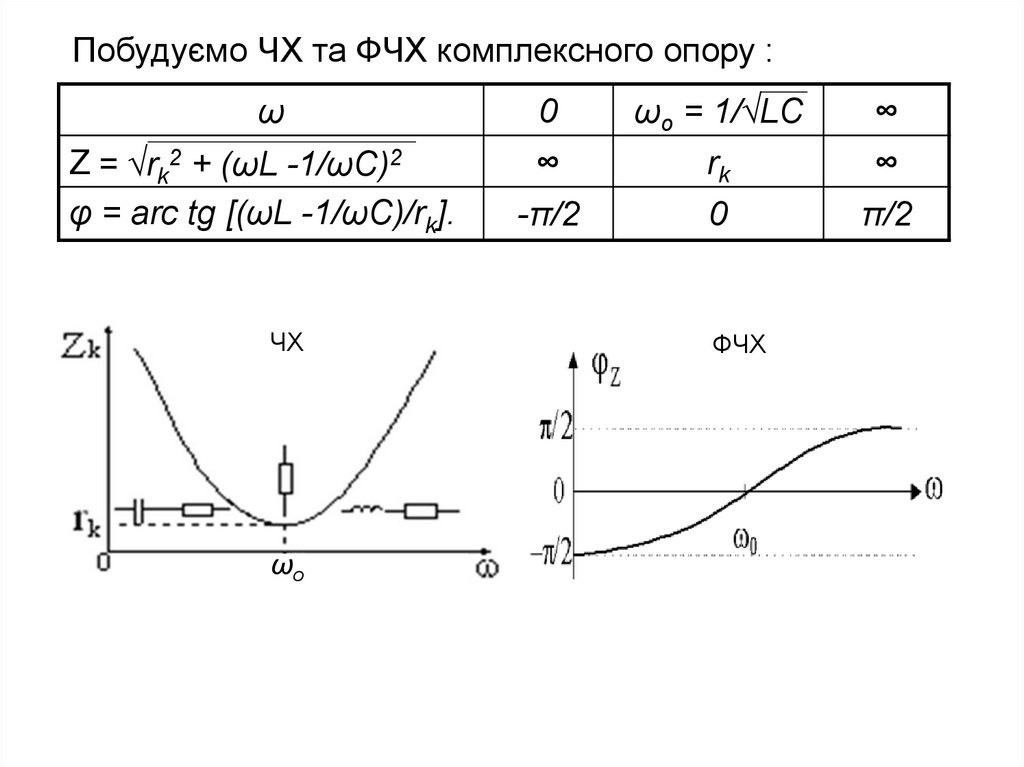
Побудуємо ЧХ та ФЧХ комплексного опору :
ω
0
ωо = 1/√LC
∞
Z = √rk2 + (ωL -1/ωC)2
φ = arc tg [(ωL -1/ωC)/rk].
∞
-π/2
rk
0
∞
π/2
ЧХ
ωо
ФЧХ

10.

З графіка АЧХ видно, що на частотах, нижчих
від резонансної опір кола має резистивно-ємнісний,
а на частотах, вищих від резонансної – резистивноіндуктивний характер, що умовно позначено на його
частотній характеристиці.
З графіка ФЧХ бачимо, що із зростанням
частоти аргумент змінюється від - /2 до /2,
проходячи через нуль на резонансній частоті 0.
Отже, на резонансній частоті вхідна напруга та
струм коливального кола збігаються за фазою.
Режим роботи послідовного коливального кола,
при якому реактивна складова комплексного
вхідного опору дорівнює нулеві, називають
резонансом.

11.

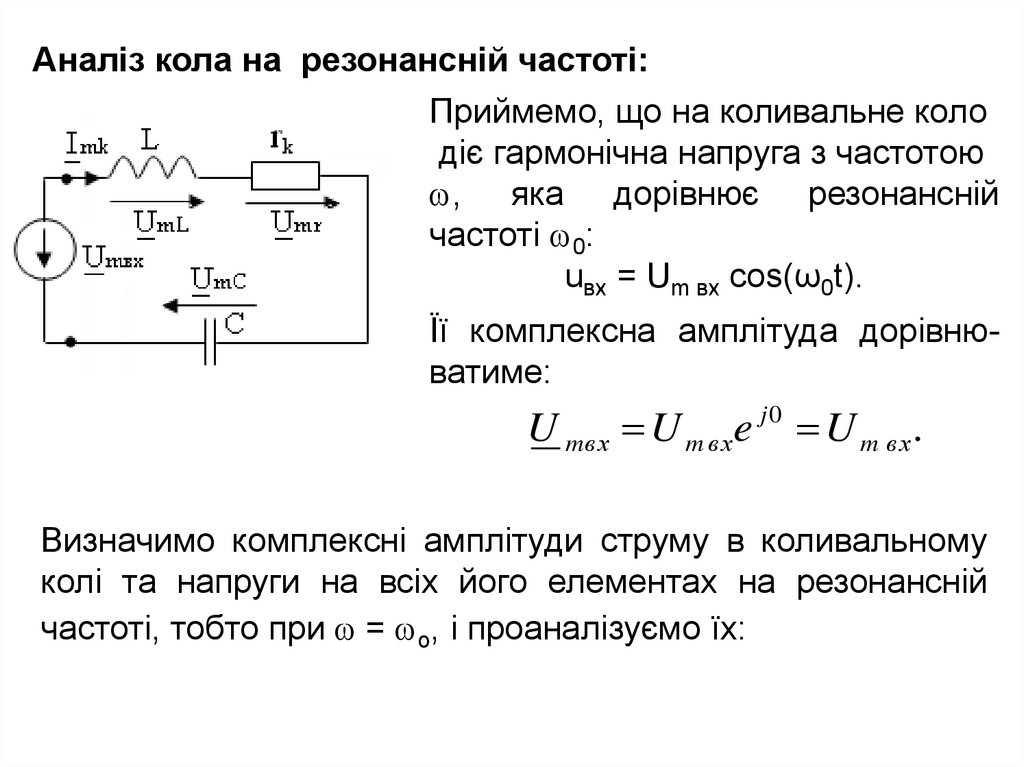
Аналіз кола на резонансній частоті:
Приймемо, що на коливальне коло
діє гармонічна напруга з частотою
, яка дорівнює резонансній
частоті 0:
uвх = Um вх cos(ω0t).
Її комплексна амплітуда дорівнюватиме:
U mвх U m вхe j 0 U m вх .
Визначимо комплексні амплітуди струму в коливальному
колі та напруги на всіх його елементах на резонансній
частоті, тобто при = o, і проаналізуємо їх:

12.

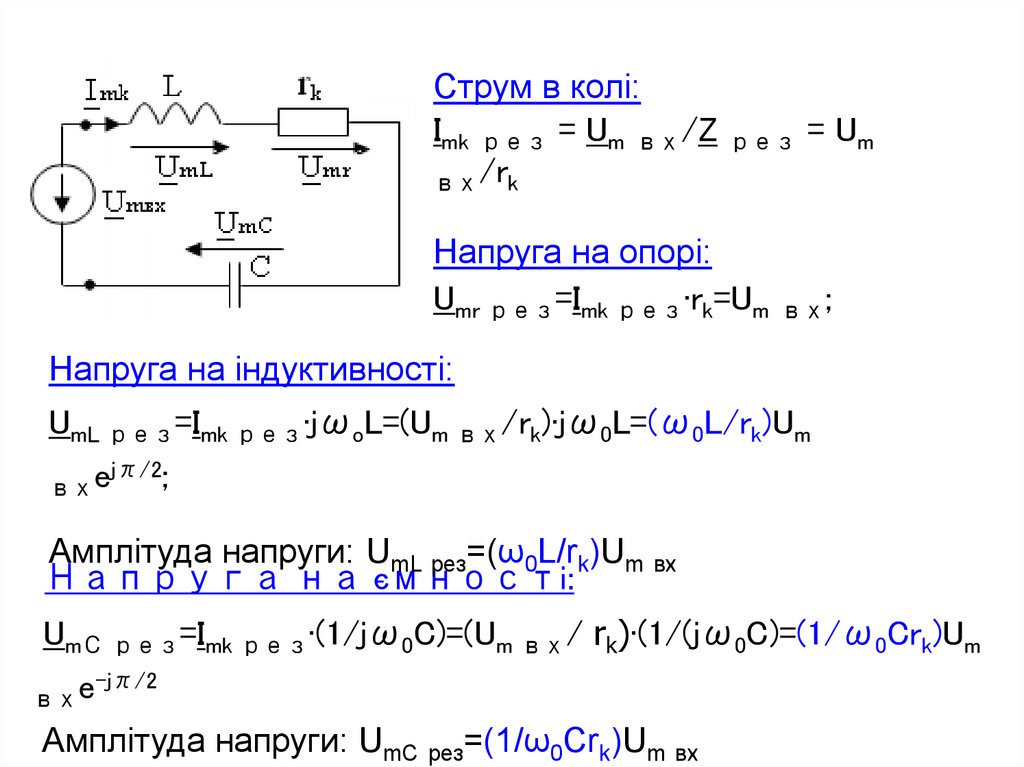
Струм в колі:
Imk рез = Um вх/Z рез = Um
вх/rk
Напруга на опорі:
Umr рез=Imk рез∙rk=Um вх;
Напруга на індуктивності:
UmL рез=Imk рез∙jωoL=(Um вх/rk)∙jω0L=(ω0L/rk)Um
jπ/2;
e
вх
Амплітуда напруги: UmL рез=(ω0L/rk)Um вх
Напруга на ємності:
UmС рез=Imk рез∙(1/jω0C)=(Um вх/ rk)∙(1/(jω0C)=(1/ω0Crk)Um
-jπ/2
e
вх
Амплітуда напруги: UmC рез=(1/ω0Crk)Um вх

13.

Із наведених формул бачимо, що, оскільки на резонансній
частоті реактивні опори котушки та конденсатора однакові
за абсолютною величиною, то амплітуди напруг на котушці
UmLрез та на
конденсаторі UmCрез рівні між собою.
Позначимо:
Назвемо Qk - добротністю послідовного коливального кола.
Отже, можемо записати:
звідки бачимо, що на резонансній частоті амплітуди напруг
на реактивних компонентах послідовного коливального
кола рівні між собою і в Qk разів більші від амплітуди
напруги, яка діє на вході кола. Тому явище резонансу в
послідовному коливальному колі називають резонансом
напруг.

14.

Властивість коливального кола збільшувати
амплітуду коливань з частотами, близькими до
резонансної,
використовують
для
виділення
коливань заданих частот із загальної сукупності
коливань з різними частотами. Коли на коливальне
коло діє кілька коливань з різними частотами, то
коливання, частота якого співпадає з резонансною
кола, будуть збільшені в Qk разів. Коливання інших
частот будуть тим слабшими, чим далі їхні частоти
від резонансної.
uС
A
uвх
0
uвх
t
0
uС
t
t

15.

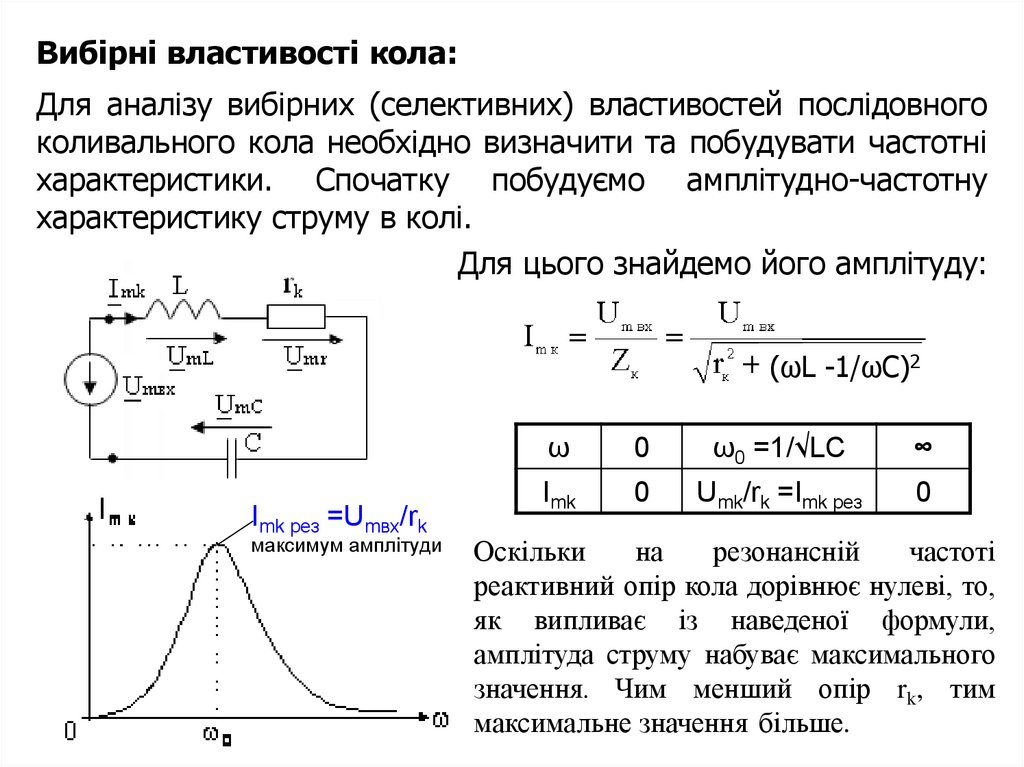
Вибірні властивості кола:
Для аналізу вибірних (селективних) властивостей послідовного
коливального кола необхідно визначити та побудувати частотні
характеристики. Спочатку побудуємо амплітудно-частотну
характеристику струму в колі.
Для цього знайдемо його амплітуду:
(ωL -1/ωC)2
Imk рез =Umвх/rk
максимум амплітуди
ω
0
ω0 =1/√LC
∞
Imk
0
Umk/rk =Imk рез
0
Оскільки
на
резонансній
частоті
реактивний опір кола дорівнює нулеві, то,
як випливає із наведеної формули,
амплітуда струму набуває максимального
значення. Чим менший опір rk, тим
максимальне значення більше.

16.

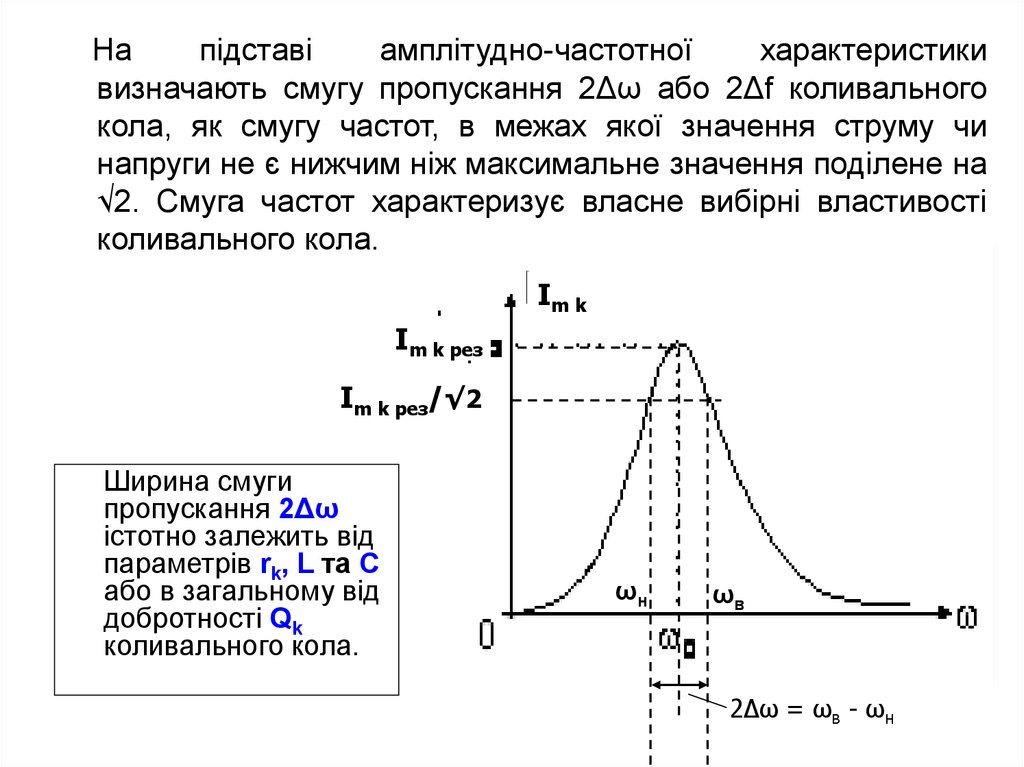
На
підставі
амплітудно-частотної
характеристики
визначають смугу пропускання 2Δω або 2Δf коливального
кола, як смугу частот, в межах якої значення струму чи
напруги не є нижчим ніж максимальне значення поділене на
√2. Смуга частот характеризує власне вибірні властивості
коливального кола.
Im k
Im k рез
Im k рез/√2
Ширина смуги
пропускання 2Δω
істотно залежить від
параметрів rk, L та C
або в загальному від
добротності Qk
коливального кола.
ωн
ωв
2Δω = ωв - ωн

17.

Для врахування впливу вище згаданих параметрів на АЧХ
виразимо комплексний опір коливального кола через
його добротність.
Zk = rk + jωL + 1/jωC = rk + j[ωL –1/(ωC)] =
L
L / C 0
rk j
( LC 1 /( LC )) rk 1 j
rk 0
C
rk 1 jQ k ( 1 / ) ,
де:
L/C
Qk
rk
rk
0
- добротність контура.
- нормована частота (безрозмірна).

18.

• Отже, комплексний опір коливального кола
Zk rk 1 jQ k ( 1 / )
• Його модуль, відповідно, дорівнюватиме:
Zk rk 1 Qk ( 1 / )
2
• Підставивши цей вираз у формулу для визначення
струму, отримаємо, що амплітуда струму буде
також залежати від добротності кола:
Um вx
I mk рез
Um вx
I mk
2
2
Zk
r 1 Q ( 1 / )
1 Q ( 1 / )
k
k
k

19.

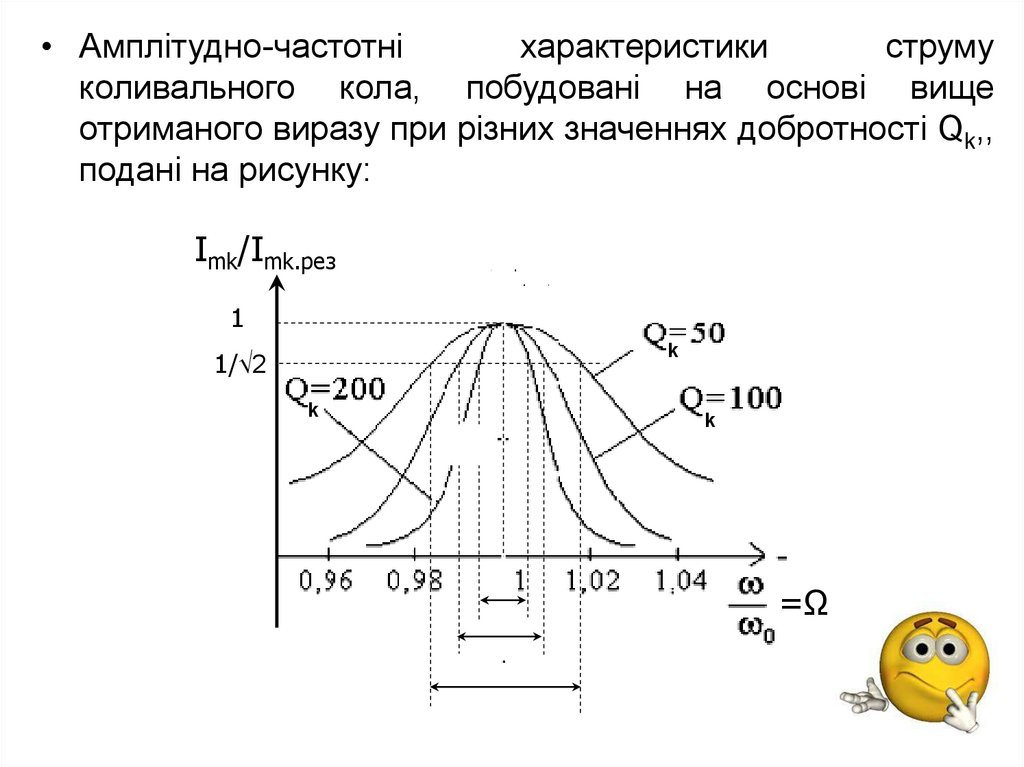
• Амплітудно-частотні
характеристики
струму
коливального кола, побудовані на основі вище
отриманого виразу при різних значеннях добротності Qk,,
подані на рисунку:
Imk/Imk.рез
1
k
1/√2
k
k
=Ω

20.

• Зауважимо, що із збільшенням добротності
резонансні криві звужуються і смуга пропускання
зменшується.
Тобто
вибірні
властивості
коливального кола зростають.
• Для високодобротних послідовних коливальних кіл
ширину смуги пропускання наближено можна
визначити за формулами:
2Δω=ω0/Qk
або
2Δf=f0/Qk
Наведені співвідношення мають важливе практичне
значення, оскільки вони описують взаємозв’язок між
шириною смуги пропускання, резонансною частотою
та добротністю коливального кола.

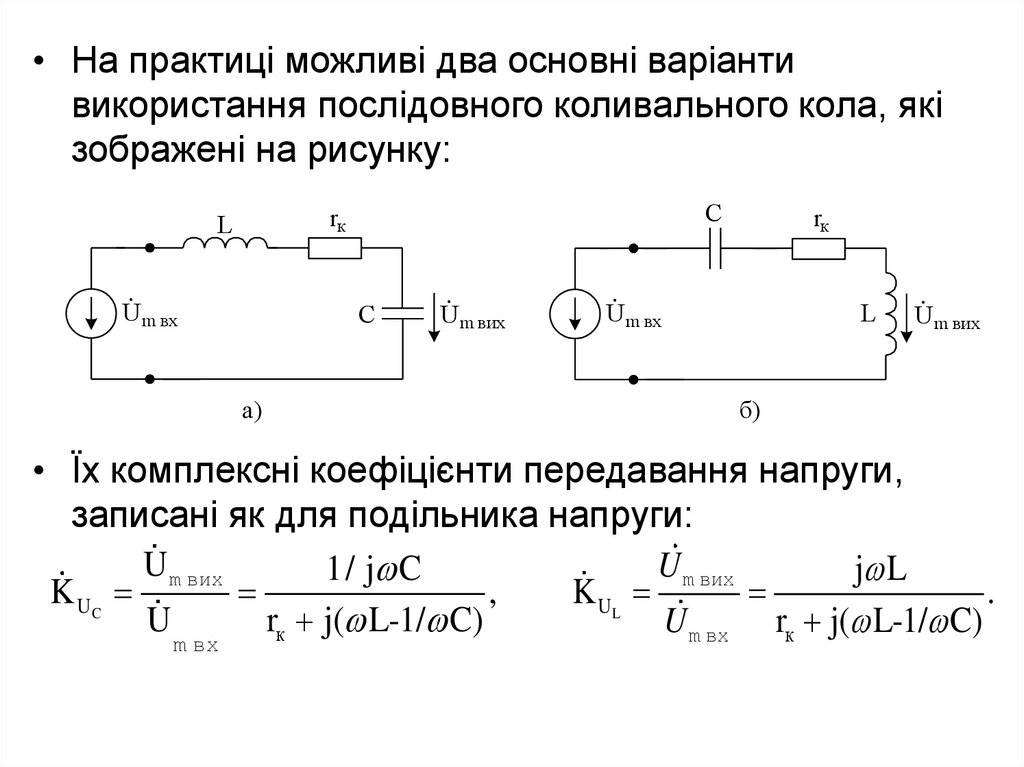
21.

• На практиці можливі два основні варіанти
використання послідовного коливального кола, які
зображені на рисунку:
C
rк
L
m вх
U
C
a)
m вих
U
rк
m вх
U
L
m вих
U
б)
• Їх комплексні коефіцієнти передавання напруги,
записані як для подільника напруги:
U m вих
U m вих
1 / j C
j L
K UC
,
K UL
.
U
rк j( L-1/ C)
U m вх rк j( L-1/ C)
m вх

22.

Модулі комплексних коефіцієнтів передавання напруги,
виражені
через
добротність
кола,
відповідно,
дорівнюватимуть:
K UC
Q k 0 /
1 [Qk ( / 0 0 / )]2
;
K UL
Q k / 0
1 [Qk ( / 0 0 / )]
2
.
Провівши дослідження цих виразів на екстремуми,
отримаємо, що вони досагають максимуму на частотах:
0C
0
1 1 / 4Q k
2
;
0L
0
1 1 / 4Q k
2
.
На них максимальні значення модулів коефіцієнта
передавання напруги, відповідно, дорівнюватимуть:
K UC max
Qk
1 1 / 4Q k
2
K UL max
Qk
1 1 / 4Q k
2

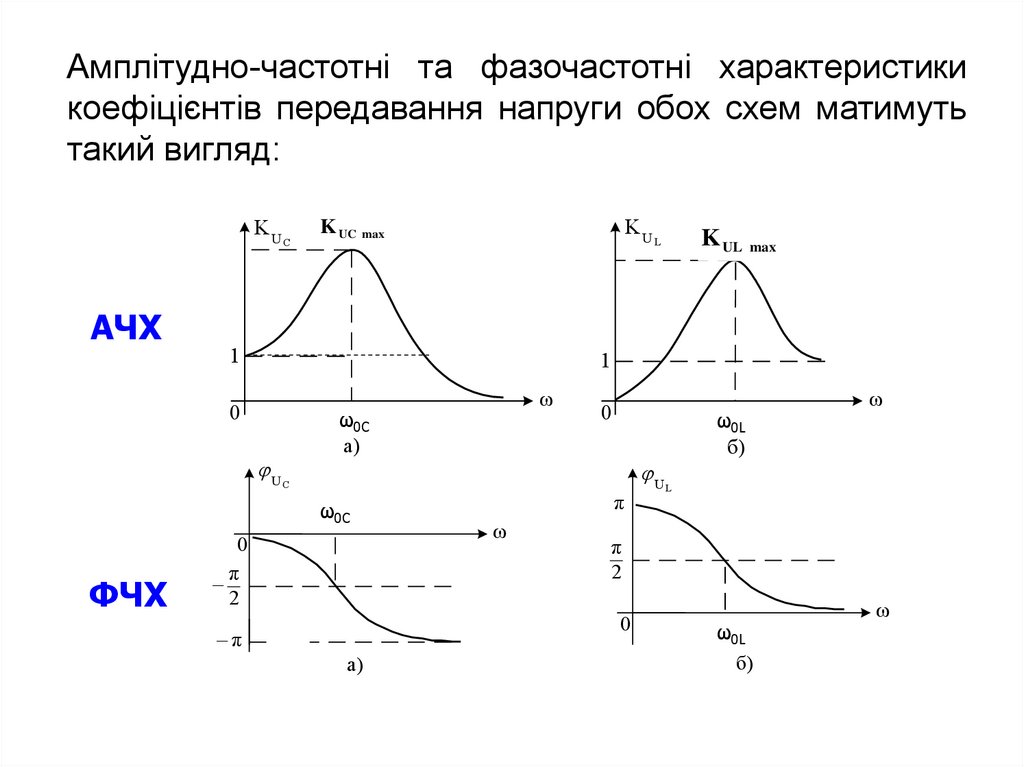
23.

Амплітудно-частотні та фазочастотні характеристики
коефіцієнтів передавання напруги обох схем матимуть
такий вигляд:
KU
АЧХ
C
1
ω
ω0
ω
0С
U
0
π
2
K UL max
L
1
0
ФЧХ
KU
K UC max
ω0
0
ω0L
a)
б)
C
ω0С
ω0
π
ω
a)
U
L
π
2
0
π
ω
ω
ω00L
б)
ω

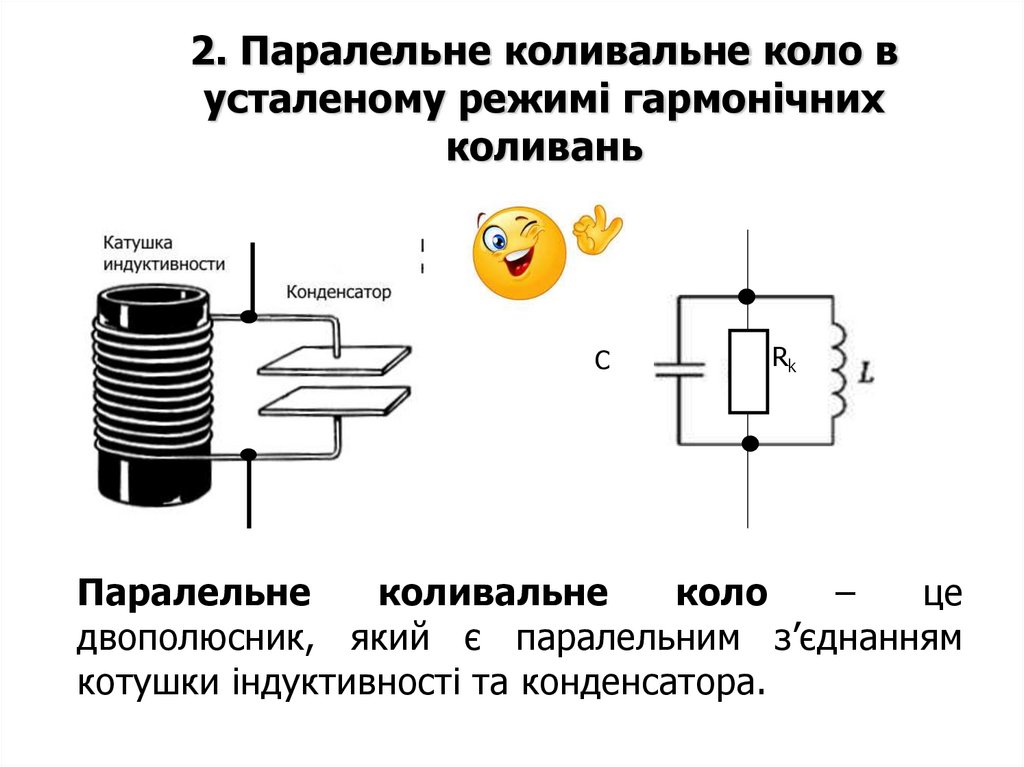
24.

2. Паралельне коливальне коло в
усталеному режимі гармонічних
коливань
С
Rk
Паралельне
коливальне
коло
–
це
двополюсник, який є паралельним з’єднанням
котушки індуктивності та конденсатора.

25.

Комплексний опір
кола:
j z
K Zk
ZK Z e
С
Rk
1
1
1
Y K 1 / RK j C 1 / L G jB
G
де G 1 / RK – резистивна складова,
B ( C 1 / L) – реактивна складова
комплексної провідності
Показникова форма запису:
Zk = Zk
ejφK =
1
√G2 + B2
ej arc tg (B/G)

26.

Модуль комплексного опору:
ZK
k
1
G2 B2
1
1 / RK2 ( C 1 / L) 2
Його аргумент:
Z arc tg ( B / G ) arc tg (( C 1 / L) Rk)

27.

З отриманих виразів видно, що на деякій
частоті реактивна складова B стає рівною
нулеві, а модуль опору – мінімальним: Zk =1/Rk.
Тобто комплексний опір кола стає активним
(резистивним), бо індуктивний та ємнісний опори
взаємно компенсуються.
Частота, на якій виникає це явище з рівняння:
ωL -1/ωC = 0
буде визначатись ємністю та індуктивністю:
1
ω = 0
рад / с
LC
або
f0
1
2 LC
Гц
Цю частоту називають резонансною частотою.

28.

Отже, на резонансній частоті абсолютні значення
реактивних провідностей конденсатора і котушки
індуктивності рівні між собою:
oC 1 / o L
і при підстановці
1
0
рад / с
LC
можуть бути визначені через параметри компонентів кола:
oC 1 / oL C / L
Цей вираз відповідає так званій характеристичній
провідності коливального кола Її позначають літерою σ,
тобто:
σ = ωoС = 1/ωoL = √C/L , См
Обернену величину до σ називають характеристичним
опором: ρ = ωoL = 1/ωoC = √L/C , Ом.

29.

Частотні залежності модуля та аргументу комплексного
опору:
ω
0
ωо = 1/√LC
∞
Zk = 1/√1/RK2 + (ωC -1/ωL)2
0
Rk
0
φ = arc tg [(ωС -1/ωL)RK].
π/2
0
-π/2
φZ

30.

З графіка частотної характеристики модуля комплексного
0
опору бачимо, що на частоті
модуль комплексного
опору набуває максимального значення
.
.Z K max RK
Отже, на резонансній частоті опір паралельного
коливального кола є резистивним і дорівнює опорові
втрат кола RK.
На частотах, нижчих від резонансної опір кола має
резистивно-індуктивний.
На частотах, вищих від резонансної – резистивноємнісний характер.

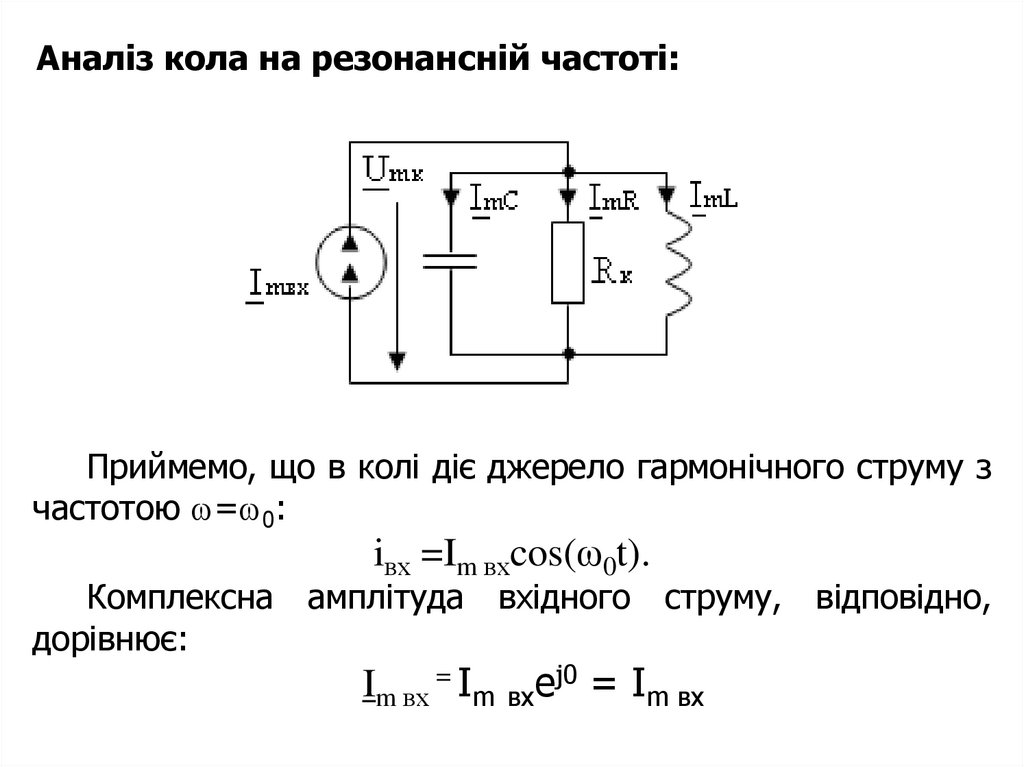
31.

Аналіз кола на резонансній частоті:
Приймемo, що в колі діє джерело гармонічного струму з
частотою = 0:
iвх =Im вхcos(ω0t).
Комплексна амплітуда вхідного струму, відповідно,
дорівнює:
Im вх = Im вхej0 = Im вх

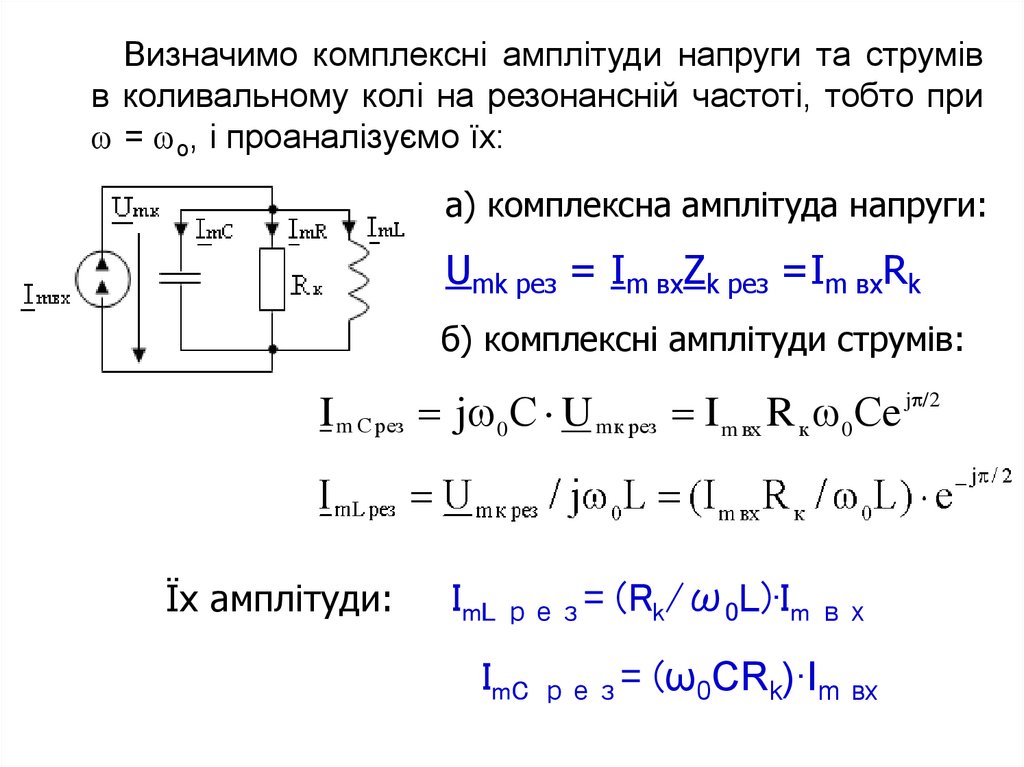
32.

Визначимо комплексні амплітуди напруги та струмів
в коливальному колі на резонансній частоті, тобто при
= o, і проаналізуємо їх:
а) комплексна амплітуда напруги:
Umk рез = Im вхZk рез =Im вхRk
б) комплексні амплітуди струмів:
I m С рез j 0 С U m к рез I m вх R к 0 Сe j /2
Їх амплітуди:
ImL рез= (Rk/ω0L)∙Im вх
ImC рез= (ω0СRk)∙Im вх

33.

Із наведених формул бачимо, що амплітуди
струму на котушці ImL рез та на конденсаторі ІmC рез
рівні між собою, оскільки на резонансній частоті
реактивні провідності котушки та конденсатора
однакові.
Позначимо Rk/ω0L= ω0СRk= Rk/ρ =Qk і назвемо
цю цю величину - добротність паралельного
коливального кола.
Бачимо, що добротність Qk тим більша, чим
більший опір Rk.

34.

З урахуванням
записати:
вибраного
позначення
можемо
I mL рез I mC рез І m вх Q к
Отже, на резонансній частоті амплітуди струмів
індуктивної та ємнісної гілок паралельного коливального
кола рівні між собою і в Qк разів більші від амплітуди
вхідного струму кола.
Тому
явище
резонансу
в
паралельному
коливальному колі називають резонансом струмів.

35.

Вибірні властивості кола:
Вибірні властивості коливального кола визначають по
амплітудно-частотних характеристиках.
Визначимо АЧХ напруги на коливальному колі, оскільки
у разі дії вхідного гармонічного струму амплітуда напруги
пропорційна до модуля комплексного вхідного опору кола:
U m к I m вх Zк
I m вх
1/ R ( С 1/ L)
2
к
0
2
0
Отже, за формою ця характеристика подібна до АЧХ
комплексного опору контура, звідки випливає, що при
відхиленні частоти вхідного струму від резонансної
амплітуда напруги на колі різко зменшується.

36.

Umk
Umk рез
Umk рез/√2
2Δω
0
ωн ω0 ωв
ω
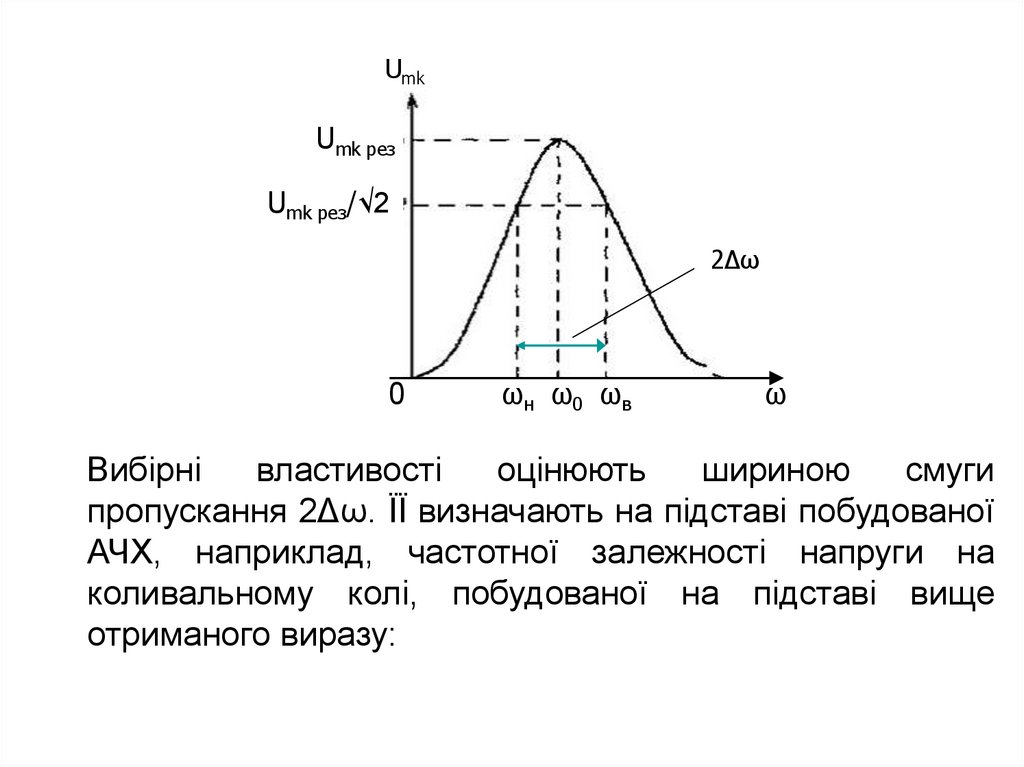
Вибірні
властивості
оцінюють
шириною
смуги
пропускання 2Δω. ЇЇ визначають на підставі побудованої
АЧХ, наприклад, частотної залежності напруги на
коливальному колі, побудованої на підставі вище
отриманого виразу:

37.

Для відображення впливу параметрів елементів Rk, L, C
або Qk на вибірні властивості кола, тобто на ширину
смуги пропускання 2Δω, виразимо комплексний опір Zk
через добротність:
Z K ZKe
j z
1
1
Y K 1 / RK j C 1 / L
1
C
1
j
( LC 1 / LC )
Rk L
Rk
R
1 j k ( / 0 0 / )
Rk
1 jQ k ( / 0 0 / )
Модуль опору: Z k
Rk
1 Q k ( / 0 0 / )
2

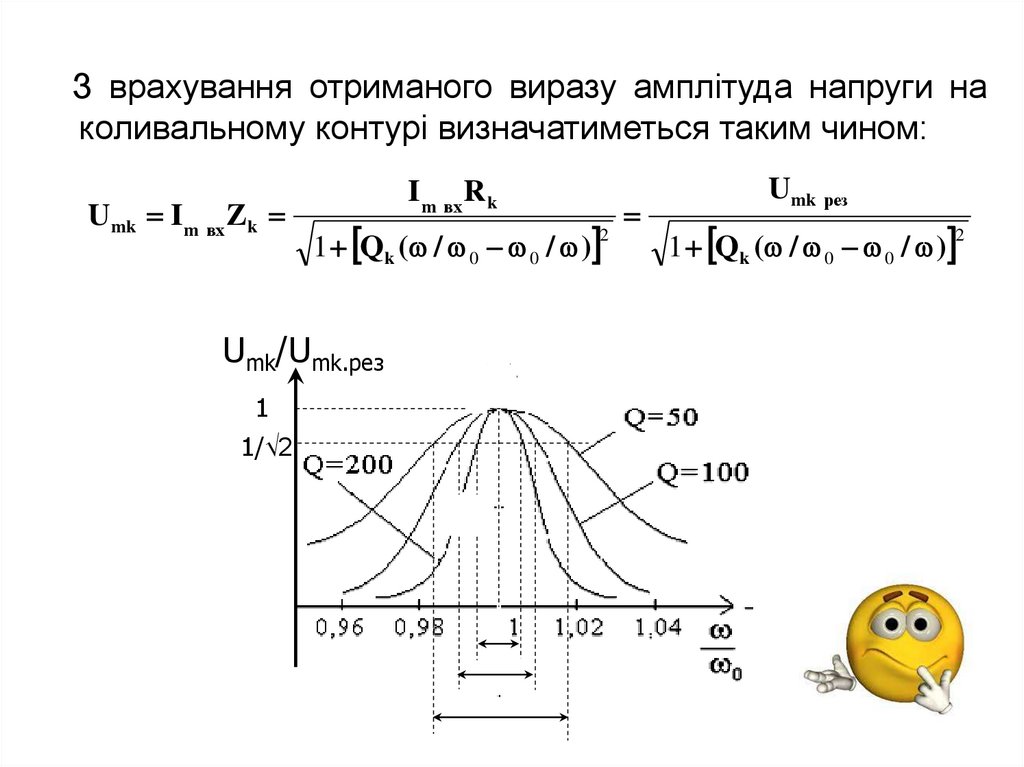
38.

З врахування отриманого виразу амплітуда напруги на
коливальному контурі визначатиметься таким чином:
Umk I m вх Zk
1 Qk ( / 0 0 / )
Umk/Umk.рез
1
1/√2
I m вх R k
2
Umk рез
1 Qk ( / 0 0 / )
2

39.

• Зауважимо, що із збільшенням добротності
резонансні
криві
звужуються
і
смуга
пропускання
зменшується.
Тобто
вибірні
властивості коливального кола зростають.
• Для високодобротних паралельних коливальних
кіл ширину смуги пропускання також наближено
визначають за формулами:
2Δω=ω0/Qk або
2Δf=f0/Qk