Similar presentations:
Нахождение оптимального результата с помощью производной в практических задачах
1.
Нахождение оптимальногорезультата с помощью
производной в практических
задачах
2.
Задачи наоптимизацию
(от лат. optimum – «наилучший») –
задачи, которые возникают там,
где необходимо выяснить
как с помощью имеющихся средств
достичь наилучшего результата
3.
Схема решениязадачи на оптимизацию
1.
Составление математической модели.
Задача «переводится» на язык функций.
Для этого выбирают удобный параметр х, через который
интересующую нас величину выражают как функцию f(x);
2. Работа с составленной моделью.
Средствами анализа ищется наибольшее или наименьшее
значение этой функции на некотором промежутке;
3. Ответ на вопрос задачи.
Выясняется, какой практический смысл (в терминах
первоначальной задачи) имеет полученный (на языке
функций результат).
4.
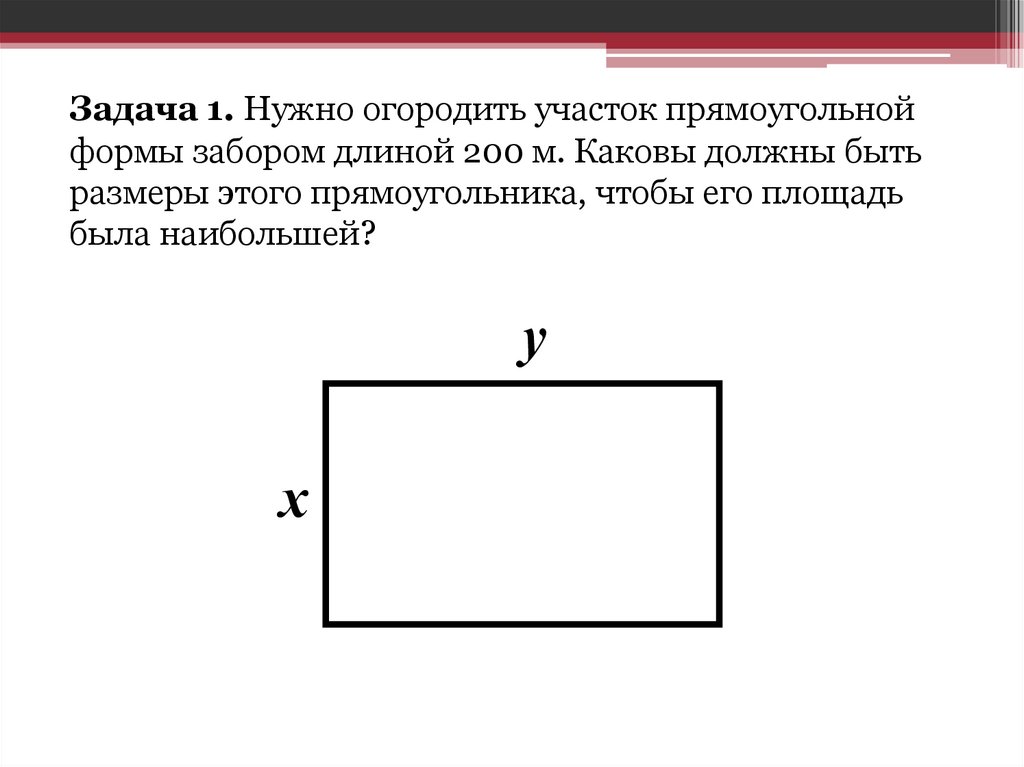
Задача 1. Нужно огородить участок прямоугольнойформы забором длиной 200 м. Каковы должны быть
размеры этого прямоугольника, чтобы его площадь
была наибольшей?
у
х
5.
Решение6.
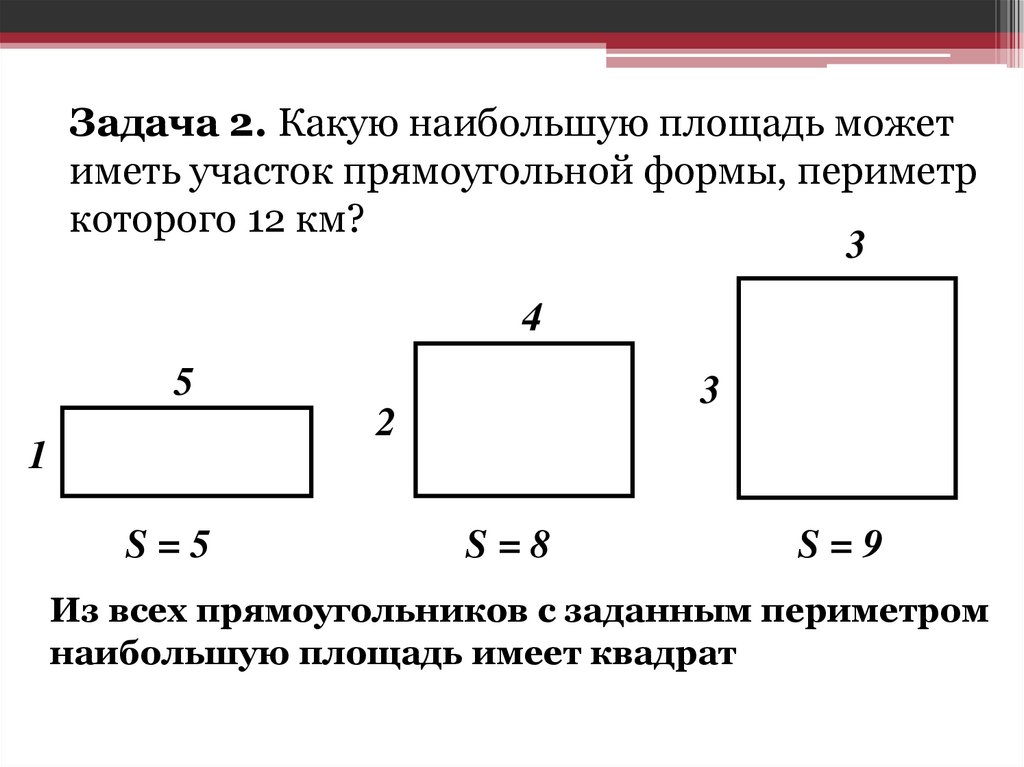
Задача 2. Какую наибольшую площадь можетиметь участок прямоугольной формы, периметр
которого 12 км?
3
4
5
3
2
1
S=5
S=8
S=9
Из всех прямоугольников с заданным периметром
наибольшую площадь имеет квадрат
7.
Задача 3. Периметр прямоугольника составляет 56 см.Каковы его стороны, если этот прямоугольник имеет
наибольшую площадь?
Задача 4. Площадь прямоугольника составляет 169 см2.
Каковы должны быть его размеры, чтобы периметр
прямоугольника был наименьшим?
8.
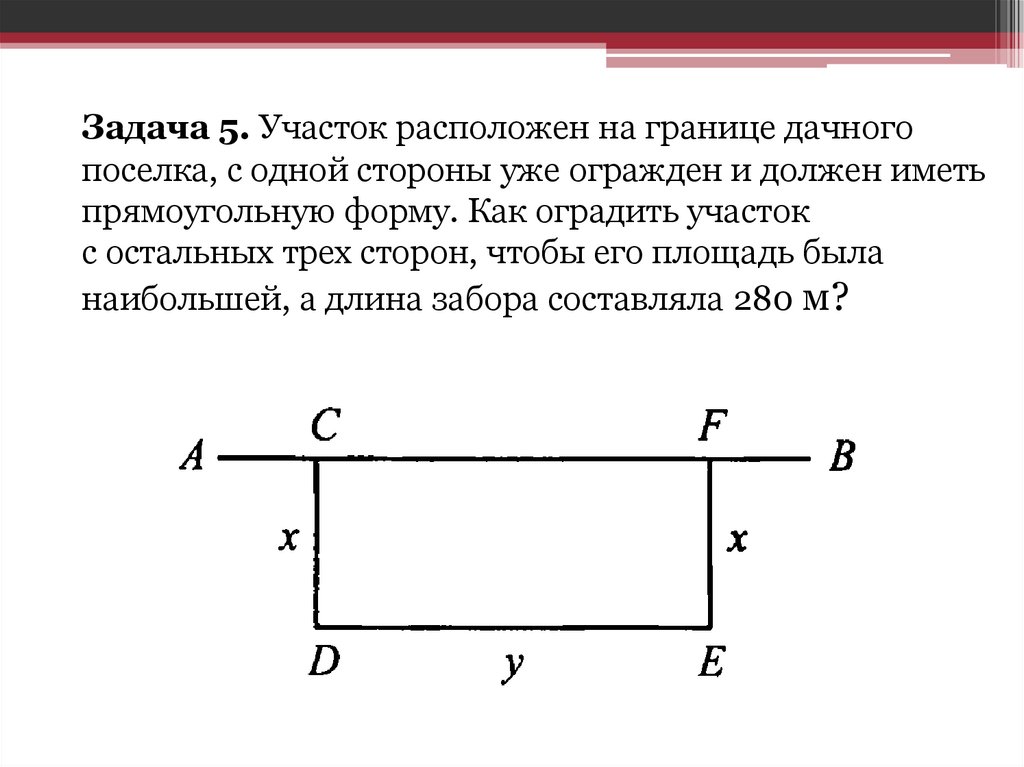
Задача 5. Участок расположен на границе дачногопоселка, с одной стороны уже огражден и должен иметь
прямоугольную форму. Как оградить участок
с остальных трех сторон, чтобы его площадь была
наибольшей, а длина забора составляла 280 м?
9.
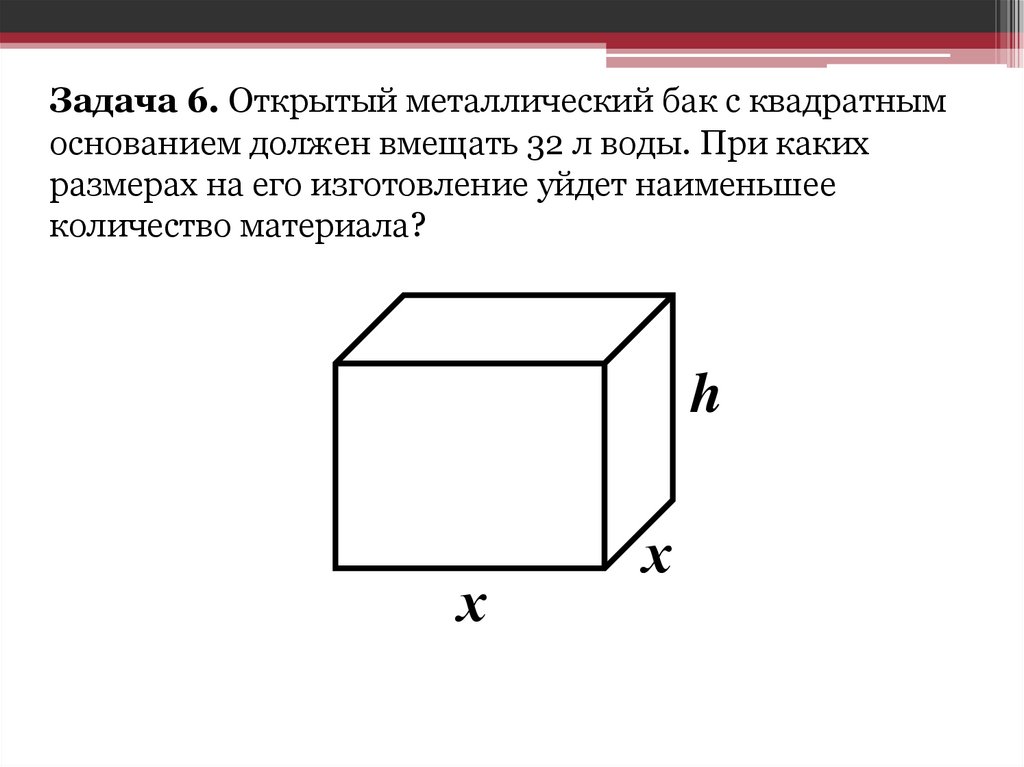
Задача 6. Открытый металлический бак с квадратнымоснованием должен вмещать 32 л воды. При каких
размерах на его изготовление уйдет наименьшее
количество материала?
h
х
х





 mathematics
mathematics








