Similar presentations:
Задачи линейного программирования
1.
Задача линейного программирования2.
Одной из важных целей экономики являетсярациональное функционирование хозяйствующих
субъектов, что, как правило, предполагает
оптимальную деятельность при ограниченных
ресурсах. В ряде случаев, для решения возникающих
задач могут использоваться методы линейного
программирования.
3.
В математике существует класс задач, которыеназываются задачами оптимизации.
Общую постановку такой задачи можно представить в
виде системы:
Если и целевая функция, и уравнения
ограничений, определяющие область допустимых
планов W, являются линейными – перед нами задача
линейного программирования
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
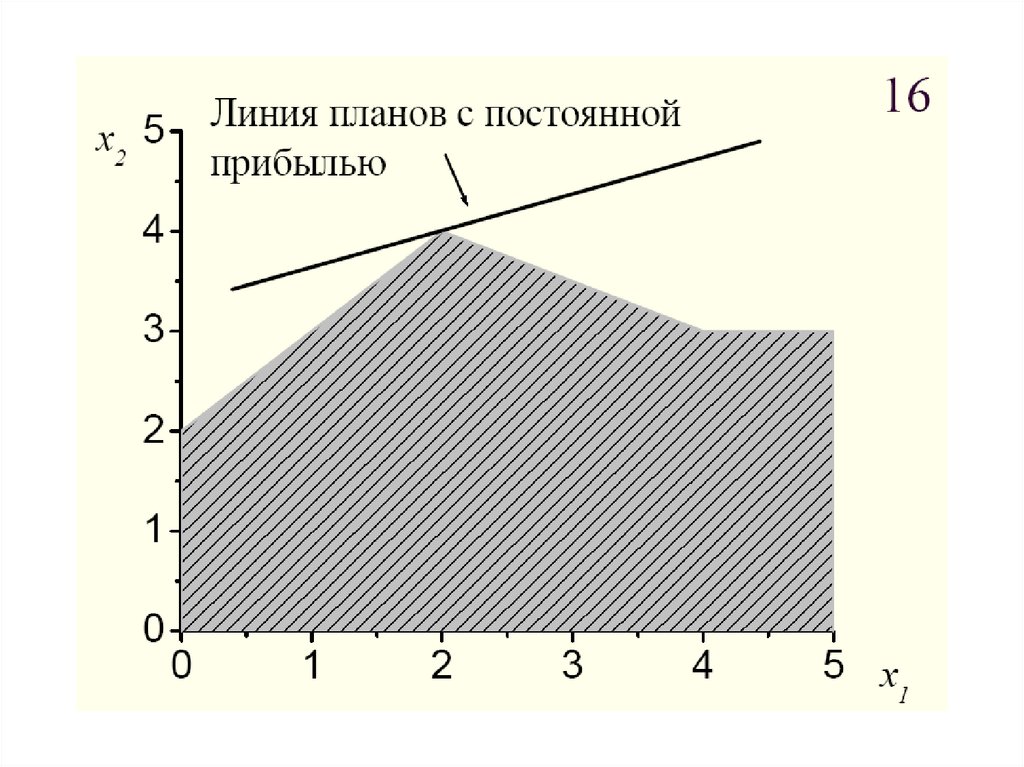
Графическое решение задач линейногопрограммирования.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
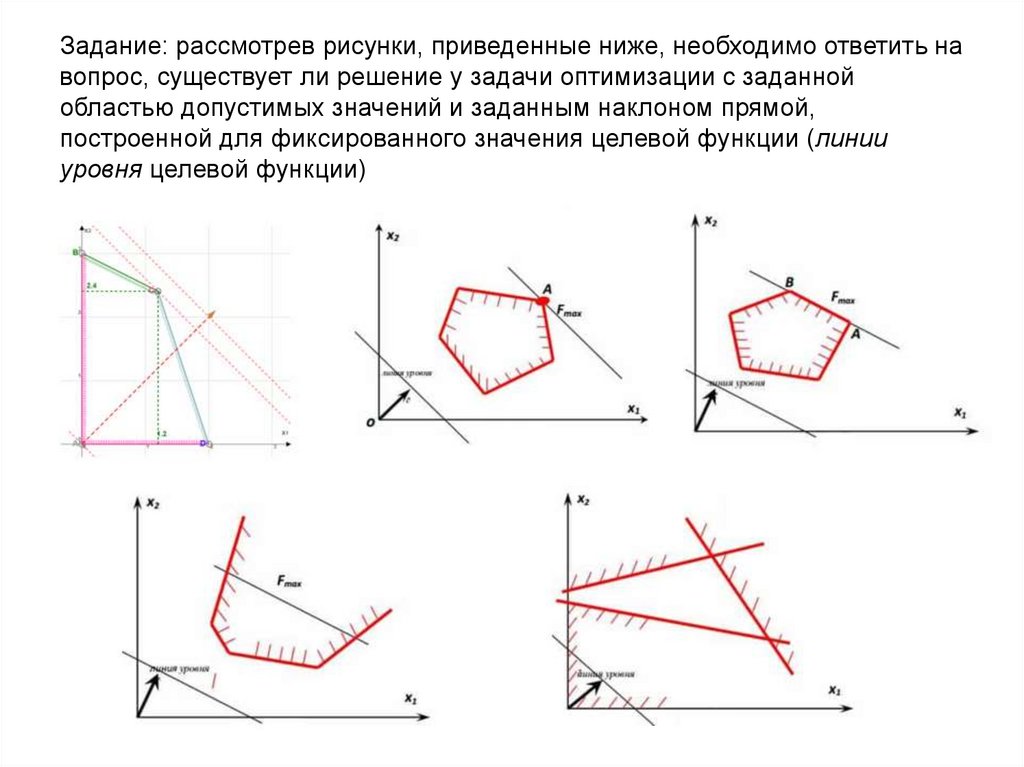
Задание: рассмотрев рисунки, приведенные ниже, необходимо ответить навопрос, существует ли решение у задачи оптимизации с заданной
областью допустимых значений и заданным наклоном прямой,
построенной для фиксированного значения целевой функции (линии
уровня целевой функции)
34.
Теоремы о решении задачи линейногопрограммирования
35.
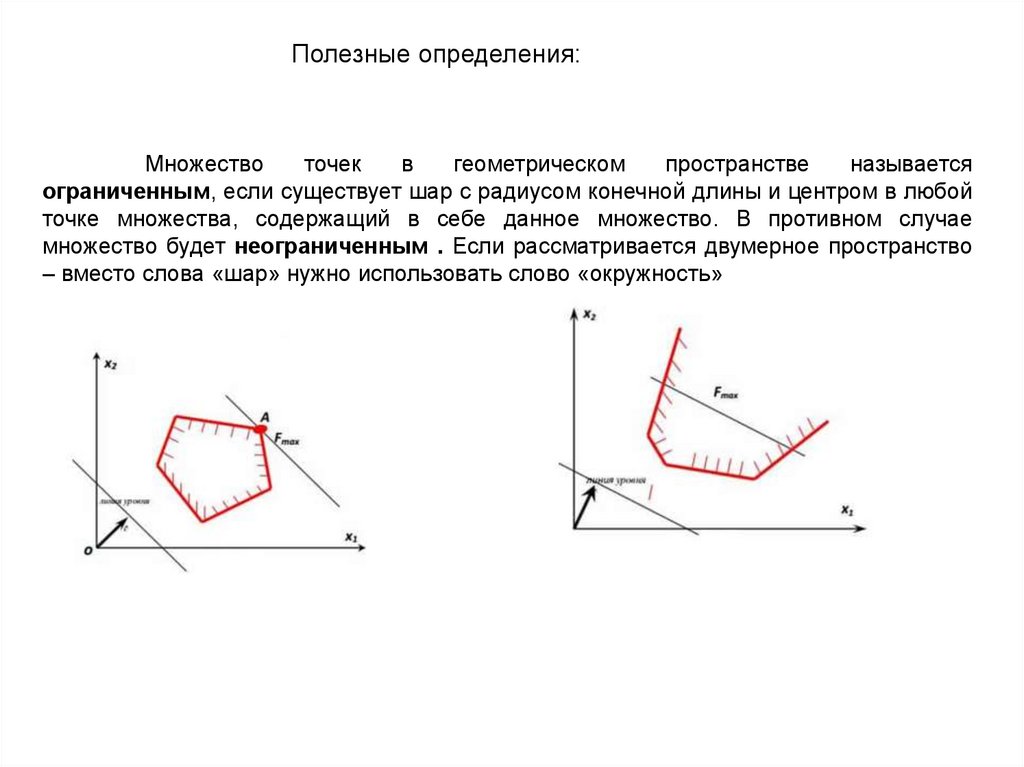
Полезные определения:Множество
точек
в
геометрическом
пространстве
называется
ограниченным, если существует шар с радиусом конечной длины и центром в любой
точке множества, содержащий в себе данное множество. В противном случае
множество будет неограниченным . Если рассматривается двумерное пространство
– вместо слова «шар» нужно использовать слово «окружность»
36.
Выпуклое множество точек:37.
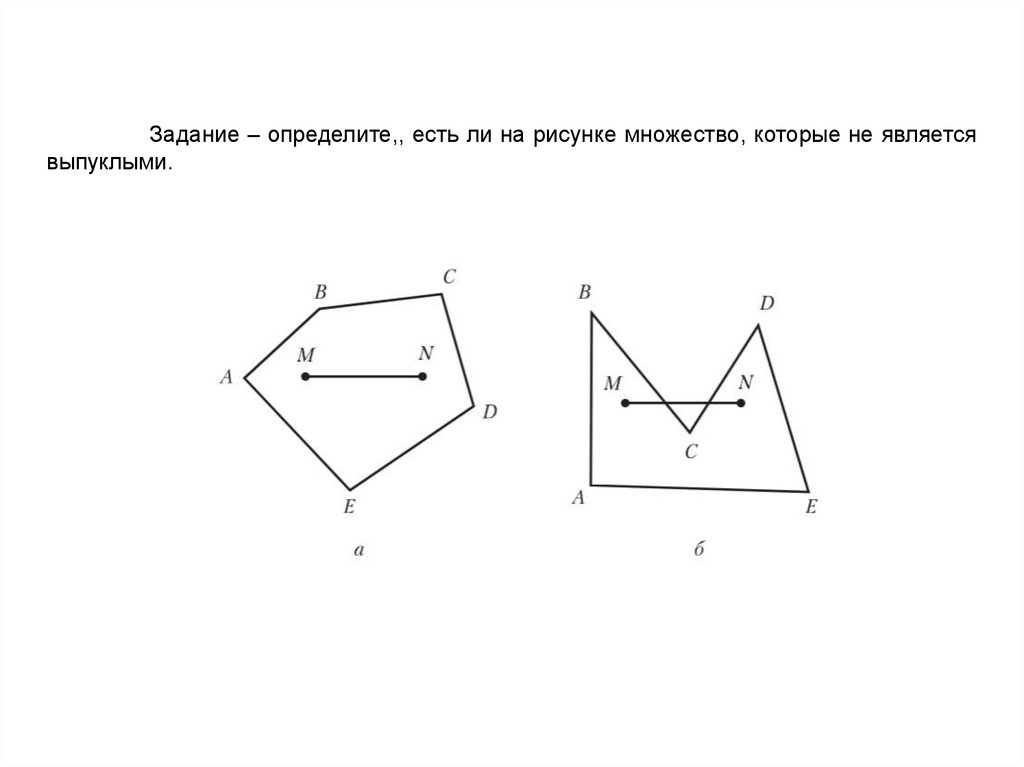
Задание – определите,, есть ли на рисунке множество, которые не являетсявыпуклыми.
38.
39.
Любая точка такой фигуры является выпуклой линейной комбинацией угловых точек40.
Матричная и векторная формы записи канонической задачилинейного программирования
Задача линейного программирования может быть записана в различных формах
41.
.42.
Выпуклая комбинация двух любых допустимых решений также является решением.При этом множество всех допустимых решений является выпуклым многогранником
или выпуклой многогранной областью.
43.
Решение задачи линейногопрограммирования методом перебора
вершин.
44.
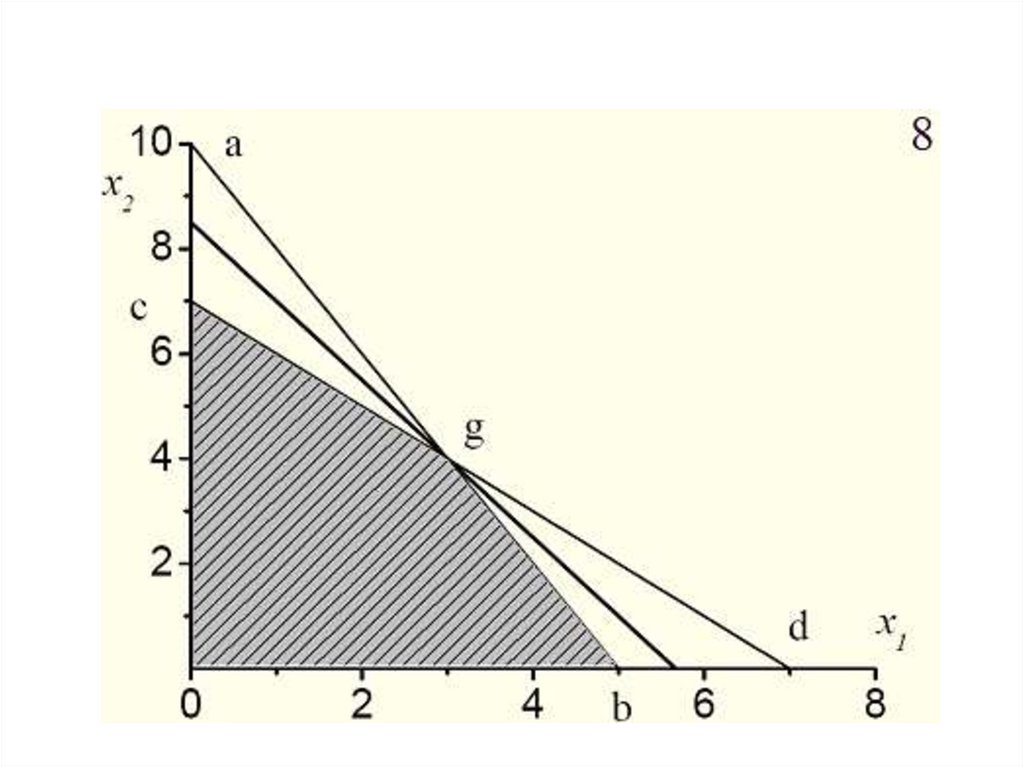
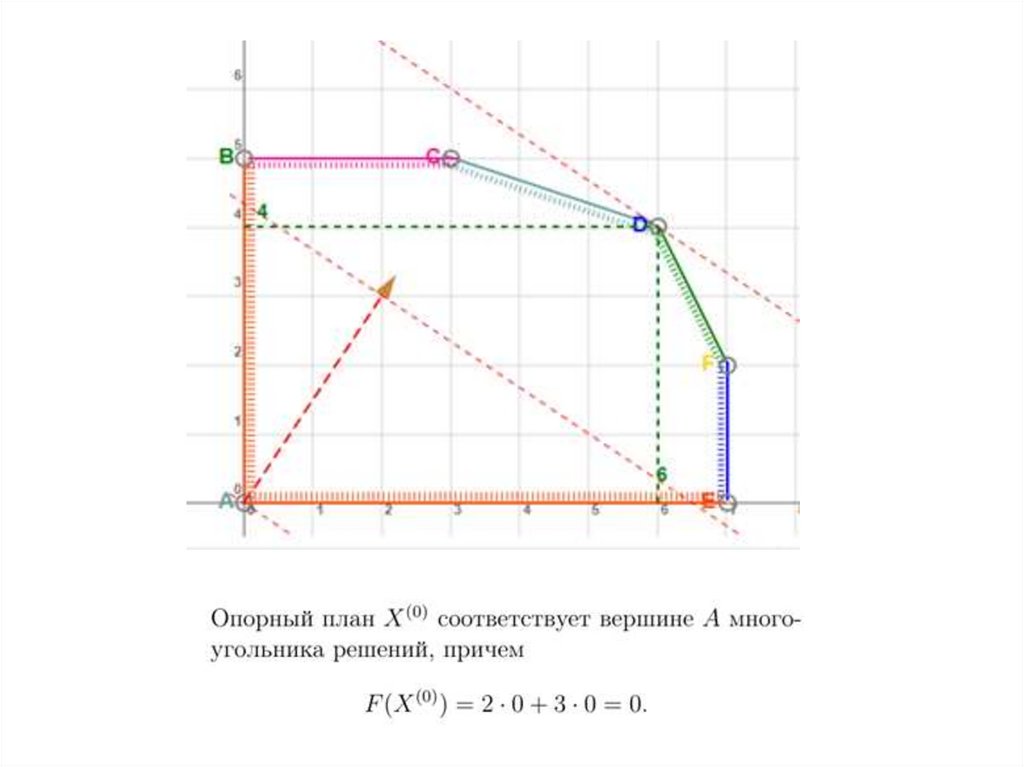
Еще раз рассмотрим рисунок, изображающий область допустимыхзначений для решенного ранее примера.
На рисунке существуют точки, не принадлежащие области
допустимых значений (хотя бы одно из ограничений не выполнено) и
точки, принадлежащие этой области (все ограничения выполняются).
В свою очередь, точки, принадлежащие области допустимых
значений, можно разделить на точки, лежащие внутри области (при
подстановке координат в систему уравнений все ограничения
выполняются в виде строгих неравенств) и точки, расположенные на
границе области допустимых значений (хотя бы одно из ограничений
выполняется в виде равенства).
Наконец, точки, лежащие на границе, могут лежать на отрезке
соединяющем две вершины полученной фигуры (для них только одно
ограничение системы обращается в равенство), либо в одной из вершин
(как минимум два ограничения, являются равенствами, определяющими
положение прямых на плоскости). Точки в вершинах области допустимых
значений носят название угловых или опорных точек.
45.
46.
Решение задачи линейной оптимизации (если оносуществует) всегда находится на границе области допустимых
значений. Это означает, что хотя бы одна из угловых точек
обязательно является решением (обеспечивает экстремальное
значение целевой функции).
В двумерном случае любая опорная точка на рисунке
принадлежит одновременно двум прямым, соответствующим двум
ограничениям задачи, взятым в виде равенства то есть является
решением системы из двух линейно-независимых уравнений с двумя
неизвестными (которые как раз и являются координатами точки).
В общем случае, в пространстве размерности n для определения
координат любой угловой точки нам понадобилось бы
рассматривать n ограничений (решать систему из n линейнонезависимых уравнений) и находить координаты точки пересечения
n линейно-независимых гиперплоскостей.
47.
Важная особенность опорных точек состоит в том, что хотя каждая изних является решением системы уравнений, построенной на основании
выбранных ограничений, далеко не каждая точка, полученная как решение
системы, построенной из n ограничений, взятых в виде равенств, является
опорной. В рассмотренном примере все опорные точки лежат на пересечении
полученных из ограничений прямых, но не все точки пересечения прямых
являются опорными (принадлежат области допустимых значений).
Соответственно, для поиска оптимального решения задачи, мы можем
использовать метод, состоящий из следующих шагов:
1. Находим все точки, которые могут быть получены путем объединения
ограничений, взятых в виде равенств, в системы из n уравнений (n-размерность
исходного пространства).
2. Проверяем полученные точки на принадлежность области допустимых
значений - определяем, выполняются ли для них все ограничения исходной
задачи. Таким образом находим среди полученных ранее точек опорные.
3. Сравниваем значение целевой функции в опорных точках. Экстремальное
значение позволяет определить точку – решение.
*Вопрос – возможно ли таким способом найти несколько решений с одним и тем
же экстремальным значением целевой функции?
48.
Симплекс-метод49.
При большом количестве ограничений полный перебор всех возможныхточек пересечения соответствующих гиперплоскостей и их анализ может
оказаться достаточно трудоемким. В подобных случаях для решения задач
может быть использован симплекс-метод. Для получения решения таким методом
необходимо:
1. Найти одну (любую) опорную точку
2. Найти все ближайшие к ней угловые точки (лежащие на ребрах многогранника,
выходящих из исходной вершины).
3. Выбрать среди полученных точек ту, в которой значение целевой функции
больше (меньше – если нужно минимизировать функцию), чем во всех
остальных.
4. Если такая точка нашлась – нужно перейти к пункту 2, если такой точки нет
(целевая функция не увеличивается при переходе в соседние вершины) –
решение найдено.
50.
Сравним две постановки задачи линейной оптимизации (стандартную иканоническую), представленные ниже.
A’=A|E
Представленная справа каноническая форма записи задачи содержит в
ограничениях только знаки равенства, благодаря введению m дополнительных
переменных (переменных «резерва»), каждая из которых равна разности между
левой и правой частью соответствующего уравнения в исходной стандартной
форме записи. Отрицательное значение любой из переменных в канонической
форме записи означает выход за область допустимых значений. В случае, если
0 равны одновременно любые n переменных канонической формы, а
остальные (m) неотрицательны – мы получаем опорную (угловую) точку.
Для построения соседних опорных точек достаточно определить, какая из m
неотрицательных переменных первой обращается в ноль при отклонении от
нуля значения одной из n переменных исходной опорной точки (при движении
вдоль «ребра» области допустимых значений).
51.
Рассмотрим этап, связанный с поиском ближайшихугловых точек.
Выбрав первую опорную точку (одну из вершин
многогранника области допустимых значений) и исключив
одно из уравнений из соответствующей этой точке системы,
мы получим координаты точек, принадлежащих прямой,
содержащей одно из ребер (В n-мерном пространстве система
n-1 линейных алгебраических уравнений задает множество
точек, являющееся аналогом прямой в трехмерном
пространстве).
Поскольку мы не хотим покидать область допустимых
значений, ограничение, которое мы исключили из системы
уравнений для опорной точки, должно по-прежнему
выполняться,
но
в
виде
неравенства,
то
есть
соответствующая ему переменная «резерва» должна иметь
положительный знак (но теперь может меняться).
52.
При движении вдоль ребра значение этойпеременной растет, но при этом меняются и значения всех
переменных «резерва» из оставшихся ограничений. Если в
процессе такого изменения
какое-либо из выполненных
неравенств исходной задачи превращается в равенство
(соответствующая ему переменная «резерва» обращается в 0)
– это означает, что мы попали в соседнюю опорную точку. Ее
координаты можно получить дополнив найденным равенством
систему из n-1 уравнений, описывающую ребро.
Таким образом, исключая (превращая в неравенство)
поочередно каждое из уравнений системы, определяющей
исходную опорную точку, и определяя, какое из ограничений
исходной задачи в каждом случае перестает выполняться
первым (при минимальном значении «освобожденной»
переменной резерва), мы находим системы уравнений для
соседних угловых точек.
Среди точек выбираем ту, в которой целевая функция
максимальна и продолжаем поиск
53.
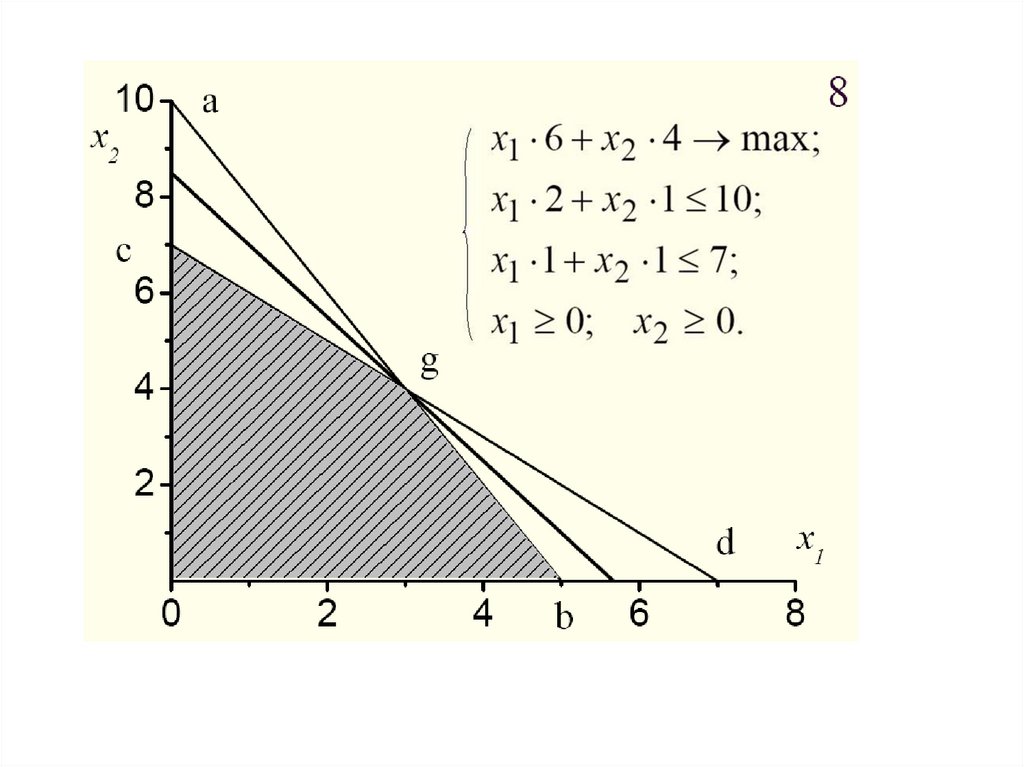
Рассмотрим пример применения симплекс-метода длядвумерного случая
54.
55.
56.
Первое ребро выберем, сохранив условие x1=0. Найдем значения x2,обращающие в 0 базисные переменные, выберем среди них
минимальное, и определим, какое из ограничений перестало
выполняться первым при движении по данному ребру. Затем
аналогичным образом рассмотрим второе ребро.
Для угловых точек:
x1=0 (x2=5) x5=0 F=15
(x1=7) x2=0 x6=0 F=14
Выбираем первый вариант
57.
58.
59.
60.
Двойственная задача линейногопрограммирования.



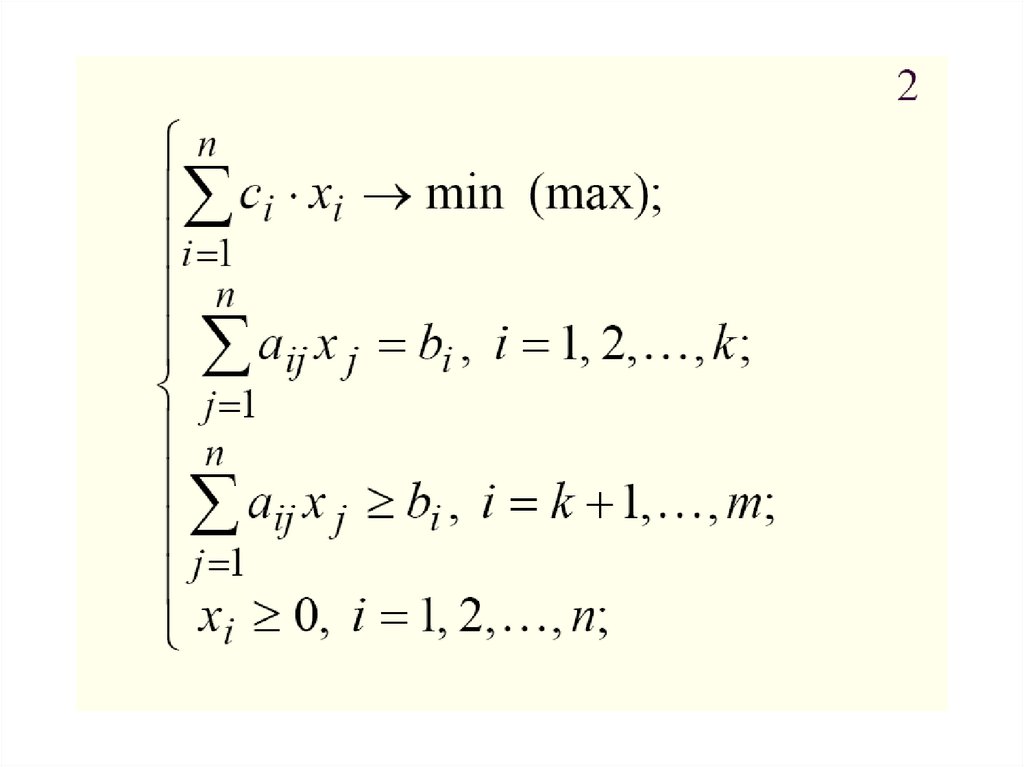



















































 mathematics
mathematics








