Similar presentations:
Свойства параллельных плоскостей
1.
Тема: «Свойствапараллельных
плоскостей».
ЦЕЛЬ:
Познакомить уч-ся со свойствами параллельных
плоскостей; повторить понятие параллельности
плоскостей; повторить признак параллельности
плоскостей; отрабатывать навыки решения задач;
развивать интерес к предмету; воспитывать у
учащихся ответственное отношение.
2.
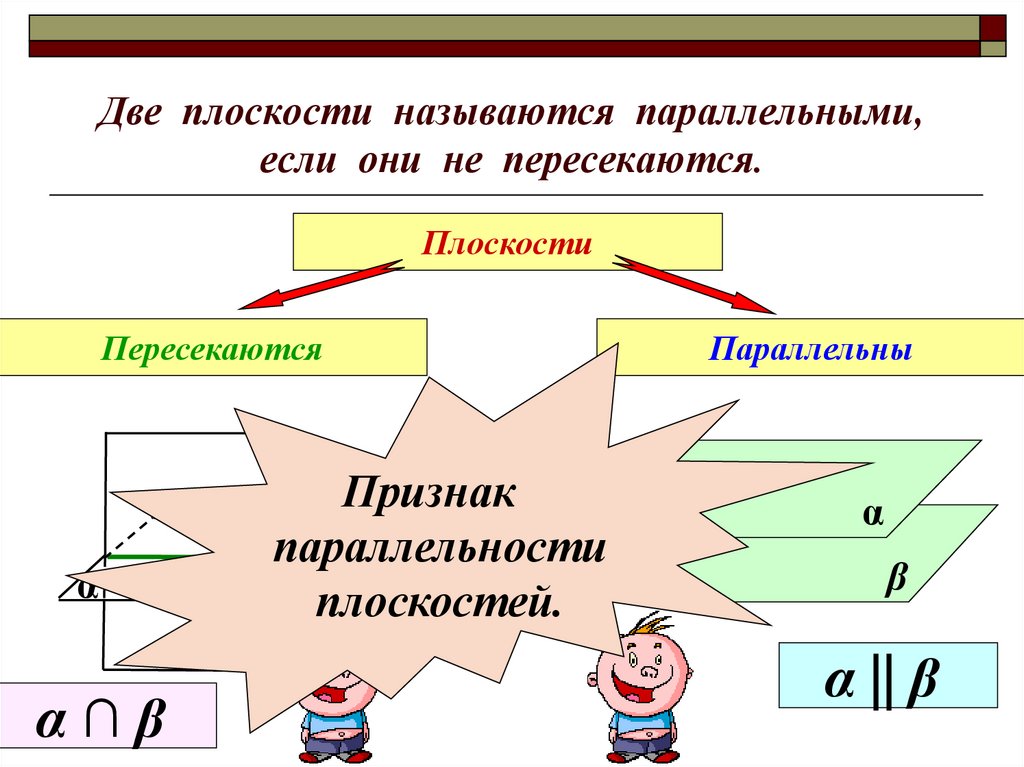
Две плоскости называются параллельными,если они не пересекаются.
Плоскости
Пересекаются
Признак
параллельности
плоскостей.
α
β
α∩β
Параллельны
α
β
α || β
3.
Карточка №1Построить и проанализировать эскизы чертежей к
возможным трём случаям взаимного расположения
прямой и плоскости в пространстве:
Прямая лежит в плоскости.
Прямая и плоскость имеют только одну точку.
3.Прямая и плоскость не имеют общих точек.
4.
Ответы к карточке №1Построить и проанализировать эскизы чертежей к
возможным трём случаям взаимного расположения
прямой и плоскости в пространстве:
Прямая лежит в плоскости.
Прямая и плоскость имеют только одну точку.
3.Прямая и плоскость не имеют общих точек.
5.
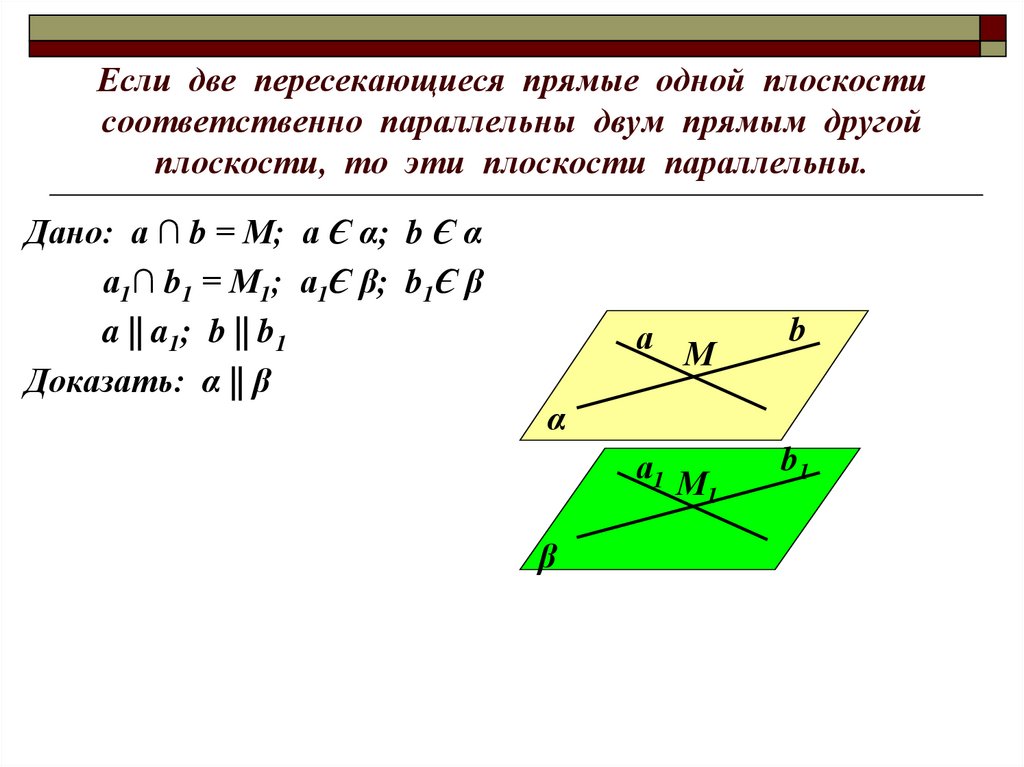
Если две пересекающиеся прямые одной плоскостисоответственно параллельны двум прямым другой
плоскости, то эти плоскости параллельны.
Дано: а ∩ b = М; а Є α; b Є α
а1∩ b1 = М1; а1Є β; b1Є β
a || a1; b || b1
Доказать: α || β
а М
b
а1 М
1
b1
α
β
6.
Если две пересекающиеся прямые одной плоскостисоответственно параллельны двум прямым другой
плоскости, то эти плоскости параллельны.
По признаку параллельности прямой и плоскости а || β и b || β.
Доказательство: (от противного)
а М
Пусть α ∩ β = с
1) Тогда а || β, т.к. a || a1, а1 Є β
а Є α; α ∩ β = с, значит а || с. α
2) b || β, т.к. b || b1, b1 Є β
а1 М
1
b Є α α ∩ β = с, значит b || с.
3) Имеем а || b, то есть
β
через точку М проходят
две прямые а и b,
параллельные прямой с.
Получили противоречие. Значит, α || β .
b
с
b1
7.
ТЕОРЕМА: Если две параллельные плоскости пересекаютсятретьей, то прямые пересечения параллельны.
ДОК-ВО: Согласно определению параллельные прямые- это
прямые ,которые лежат в одной плоскости – секущей плоскости.
Они не пересекаются ,так как не пересекаются содержащие их
параллельные плоскости. Значит, прямые параллельны.
Теорема доказана.
8.
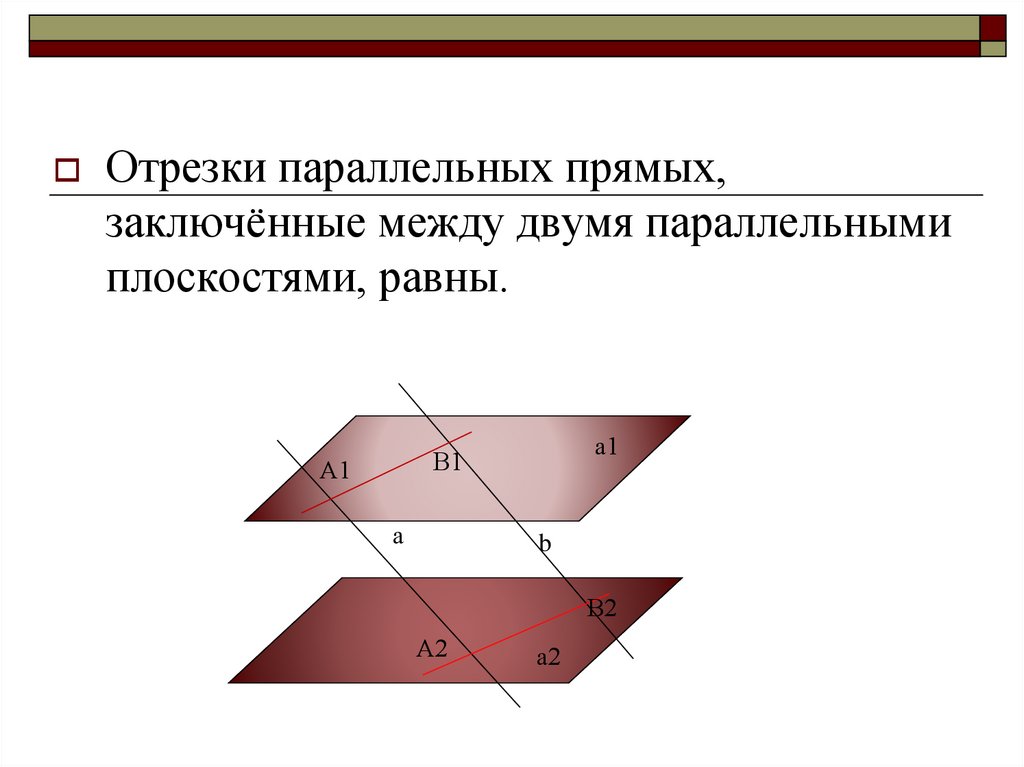
Отрезки параллельных прямых,заключённые между двумя параллельными
плоскостями, равны.
а1
В1
А1
а
b
В2
А2
а2
9.
ТестОтветьте на вопросы:
Могут ли прямая и плоскость не иметь общихДа
точек?
Нет
Верно ли, что если две прямые не пересекаются,
то они параллельны?
Плоскости α и β параллельны, прямая т лежитДав
плоскости α. Верно ли, что прямая т параллельна
плоскости β?
Верно ли, что если прямая а параллельна Нет
одной из
двух параллельных плоскостей, с другой
плоскостью прямая а имеет одну общую точку?
Верно ли, что плоскости параллельны, если
Нет
прямая, лежащая в одной плоскости, параллельна
другой плоскости?
10.
Геометрический диктант•Две прямые в пространстве называются ПАРАЛЛЕЛЬНЫМИ….
________________________________________________________
•Через точку вне данной прямой можно провести прямую,
параллельную этой прямой ,и ____________________________.
•Две прямые, параллельные третьей прямой, __________________.
•Две плоскости параллельны, если одна из них параллельна двум
пересекающимся прямым, лежащим _________________________
•Если две прямые параллельны третьей прямой, то они
_________________________________________________________
•Если одна из двух параллельных прямых пересекает данную
плоскость, то и другая прямая
_________________________________________
11.
Ответы к геометрическому диктантуДве прямые в пространстве называются
ПАРАЛЛЕЛЬНЫМИ ,если они лежат в одной плоскости и
не пересекаются.
Через точку вне данной прямой можно провести прямую,
параллельную этой прямой ,и притом только одну.
Две прямые, параллельные третьей прямой, параллельны
Две плоскости параллельны, если одна из них параллельна
двум пересекающимся прямым, лежащим в другой
плоскости
Если две прямые параллельны третьей прямой, то они
параллельны
Если одна из двух параллельных прямых пересекает данную
плоскость, то и другая прямая пересекает эту плоскость
12.
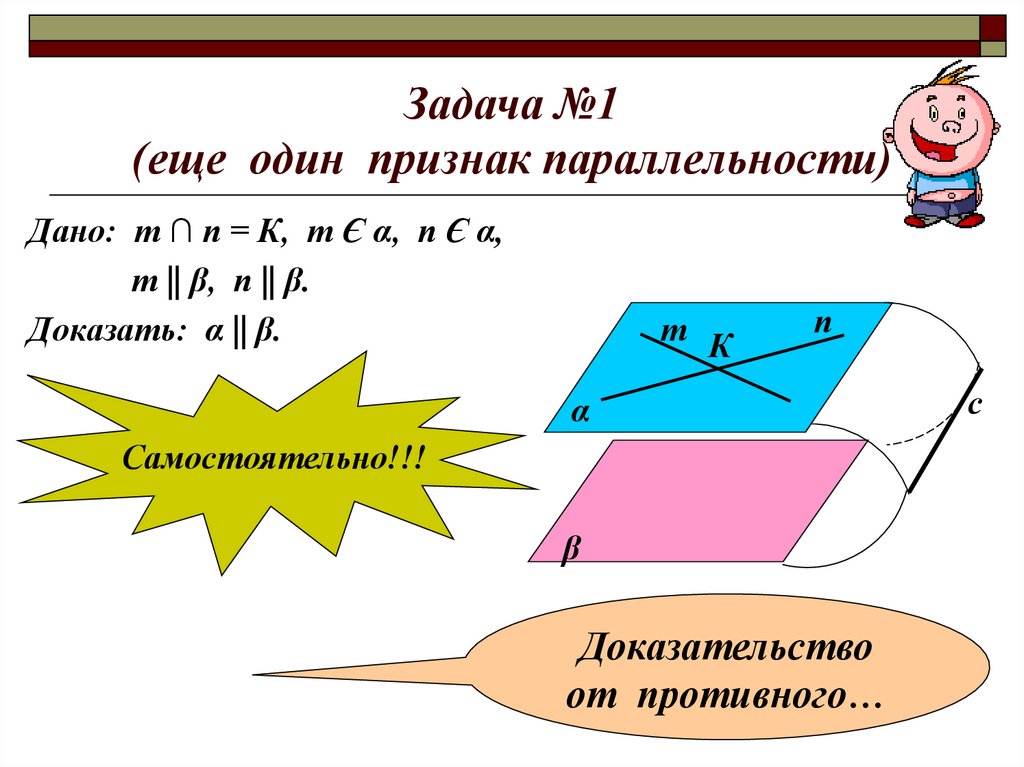
Задача №1(еще один признак параллельности)
Дано: т ∩ п = К, т Є α, п Є α,
т || β, п || β.
Доказать: α || β.
т К
п
α
Самостоятельно!!!
β
Доказательство
от противного…
с
13.
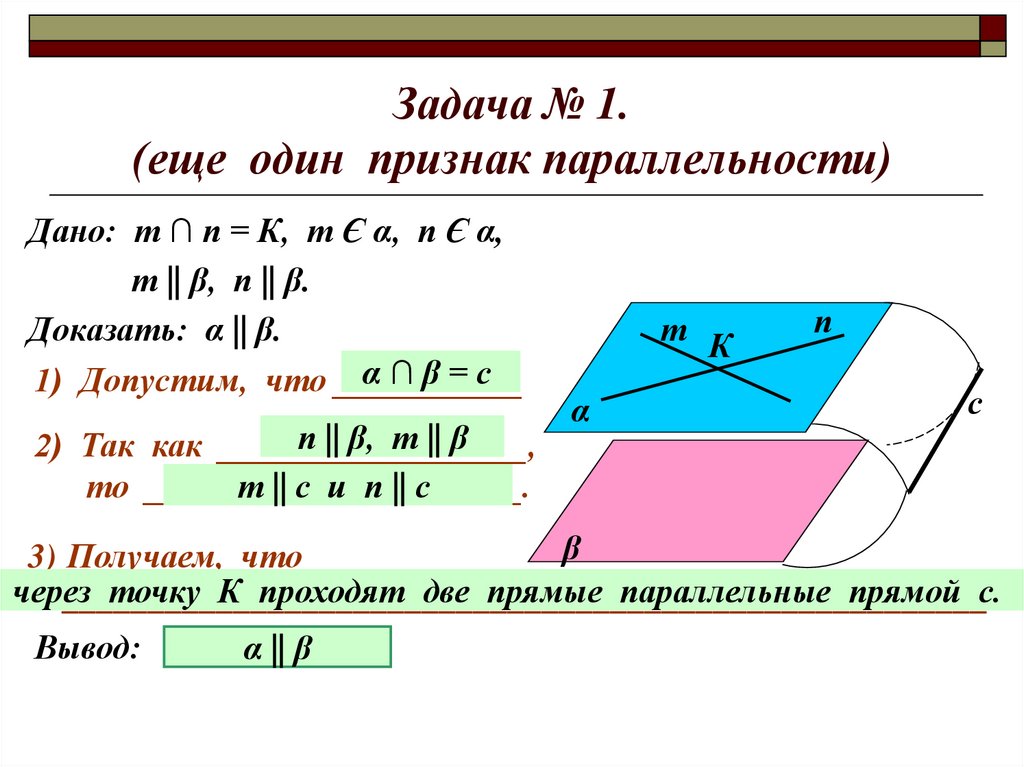
Задача № 1.(еще один признак параллельности)
Дано: т ∩ п = К, т Є α, п Є α,
т || β, п || β.
Доказать: α || β.
α∩β=с
1) Допустим, что ___________
п || β, т || β
2) Так как __________________,
т || с и п || с
то ______________________.
т К
α
п
с
β
3) Получаем, что
через
точку К проходят две прямые параллельные прямой с.
______________________________________________________.
Вывод:
α || β
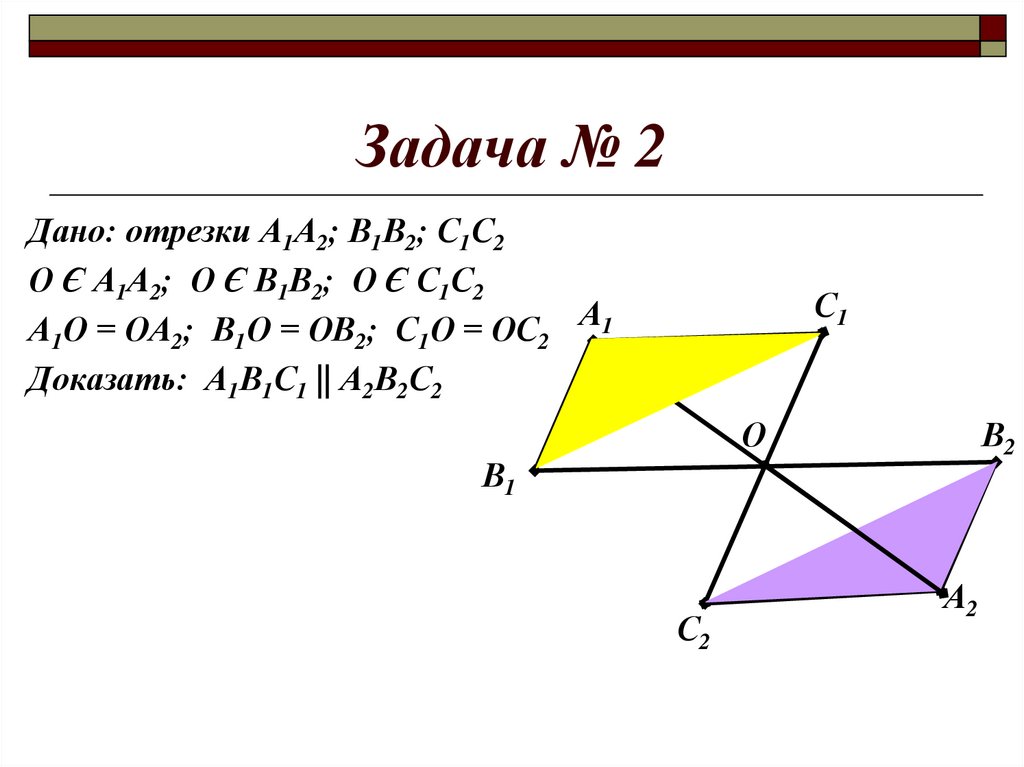
14.
Задача № 2Дано: отрезки А1А2; В1В2; С1С2
О Є А1А2; О Є В1В2; О Є С1С2
А1О = ОА2; В1О = ОВ2; С1О = ОС2 А1
Доказать: А1В1С1 || А2В2С2
С1
О
В2
В1
С2
А2
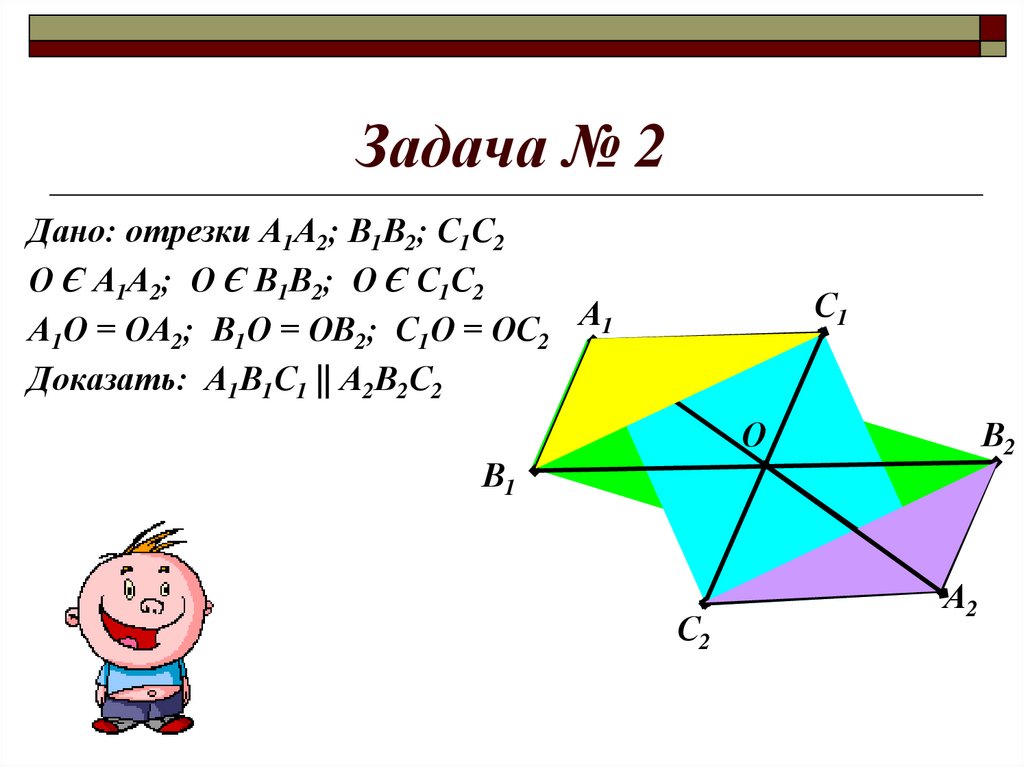
15.
Задача № 2Дано: отрезки А1А2; В1В2; С1С2
О Є А1А2; О Є В1В2; О Є С1С2
А1О = ОА2; В1О = ОВ2; С1О = ОС2 А1
Доказать: А1В1С1 || А2В2С2
С1
О
В2
В1
С2
А2
16.
Задача № 3В
N
М
C
Р
А
D
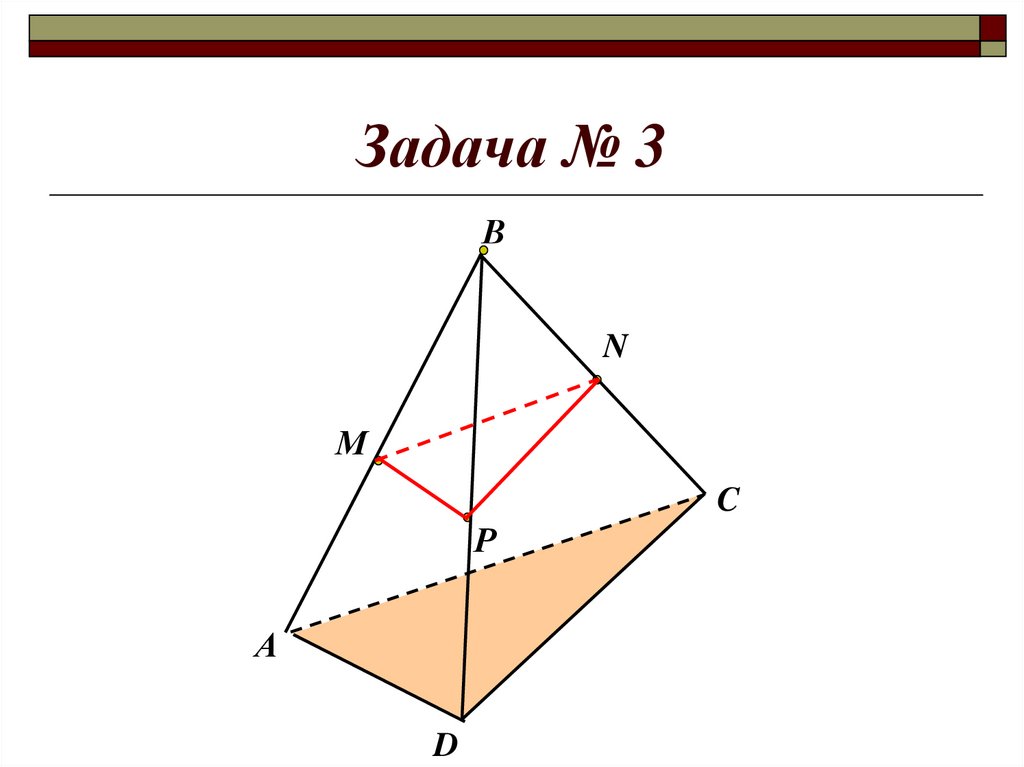
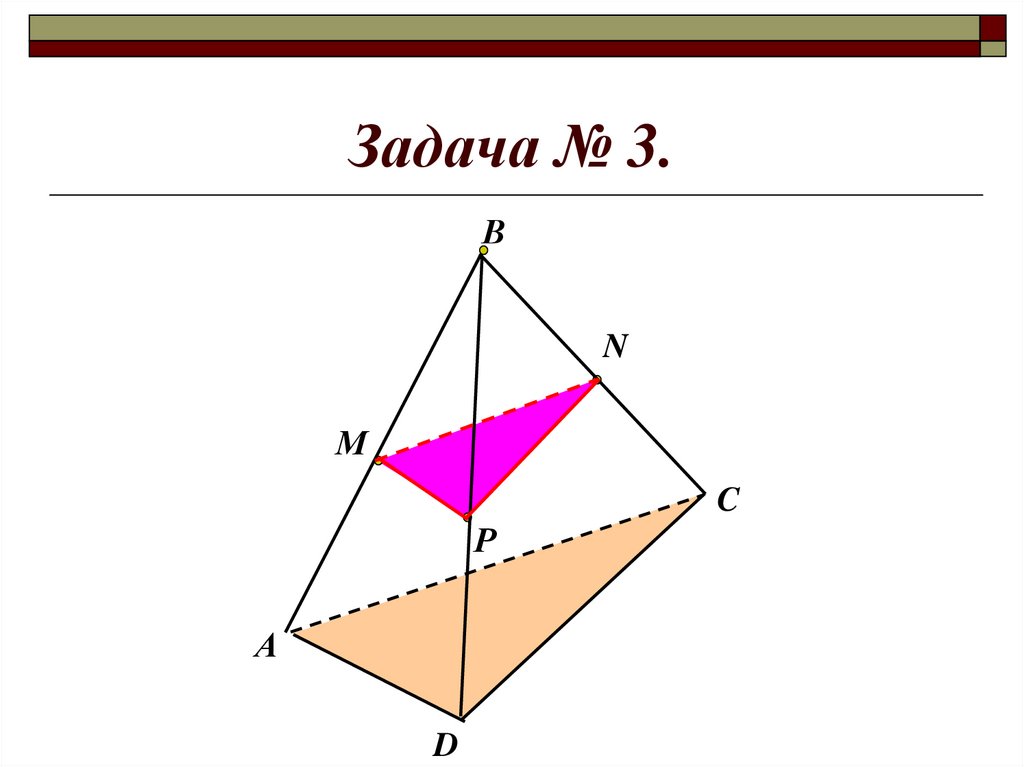
17.
Задача № 3.В
N
М
C
Р
А
D
18.
Домашнее задание:П. 10, №№ 29,30
Удачи!









 mathematics
mathematics








