Параллельность плоскостей. 10 класс

1.

2.

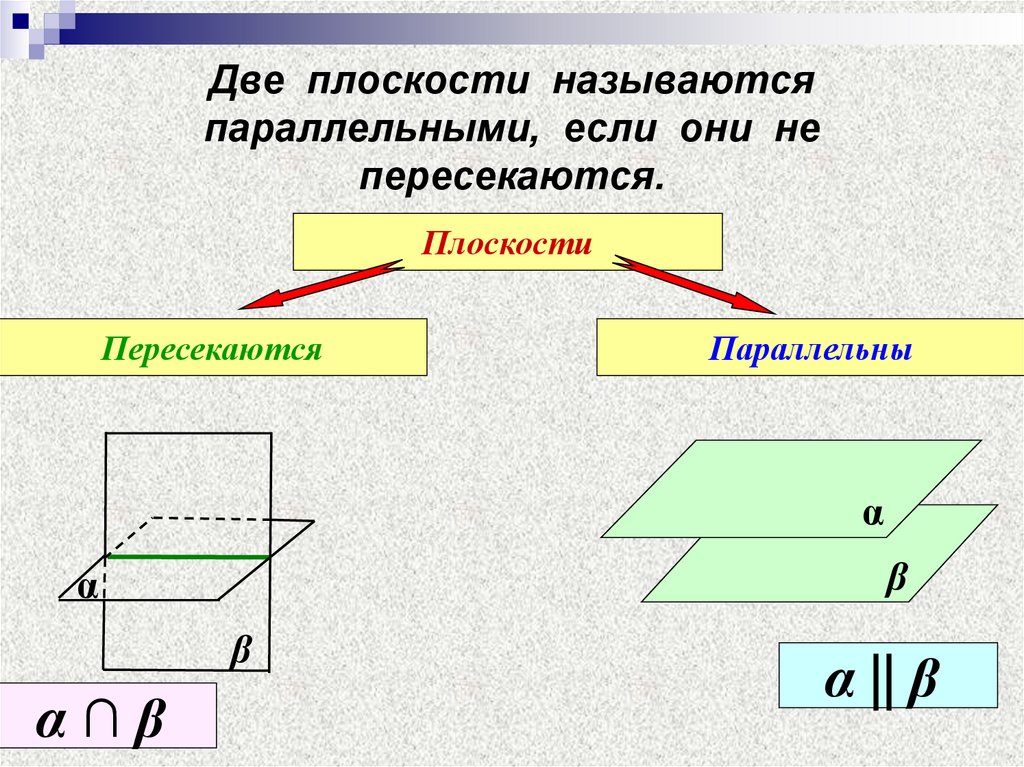
3. Две плоскости называются параллельными, если они не пересекаются.

Плоскости
Пересекаются
Параллельны
α
β
α
β
α∩β
α || β

4.

5.

а М
b
а1
b1
γ
β
М1
Дано:
а ∩ b = М; а Є ɣ; b Єɣ
а1∩ b1 = М1; а1Є β;
b1Є β
a || a1; b || b1
Доказать: ɣ || β
По признаку параллельности прямой и плоскости
а || β и b || β (Т-5)

6.

а М
b
с
γ
а1
β
М1
b1
1) Тогда а || β, т.к. a || a1, а1 Є β
а Є γ ; γ ∩ β = с, значит а||с(св.10)
2) b || β, т.к. b || b1, b1 Є β
b Є γ; γ ∩ β = с, значит b || с.
3) Имеем а || b, то есть через точку М проходят
две прямые а и b, параллельные прямой с.
Получили противоречие. Значит, γ || β .

7.

8.

9.

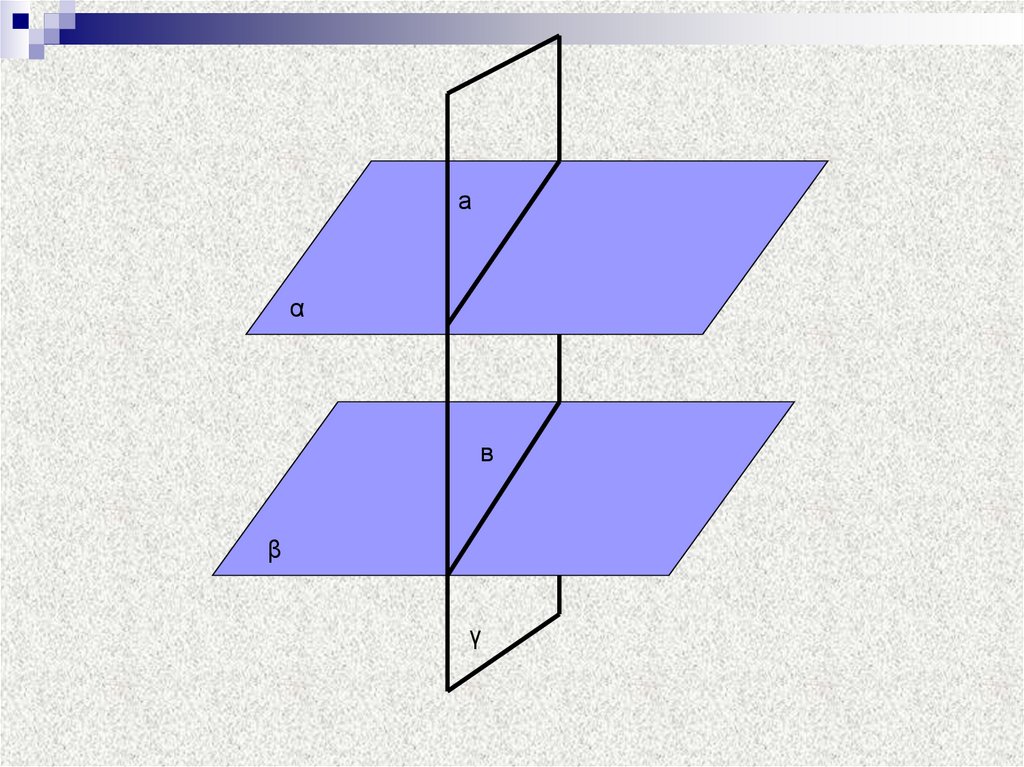
а
α
в
β
γ

10.

11.

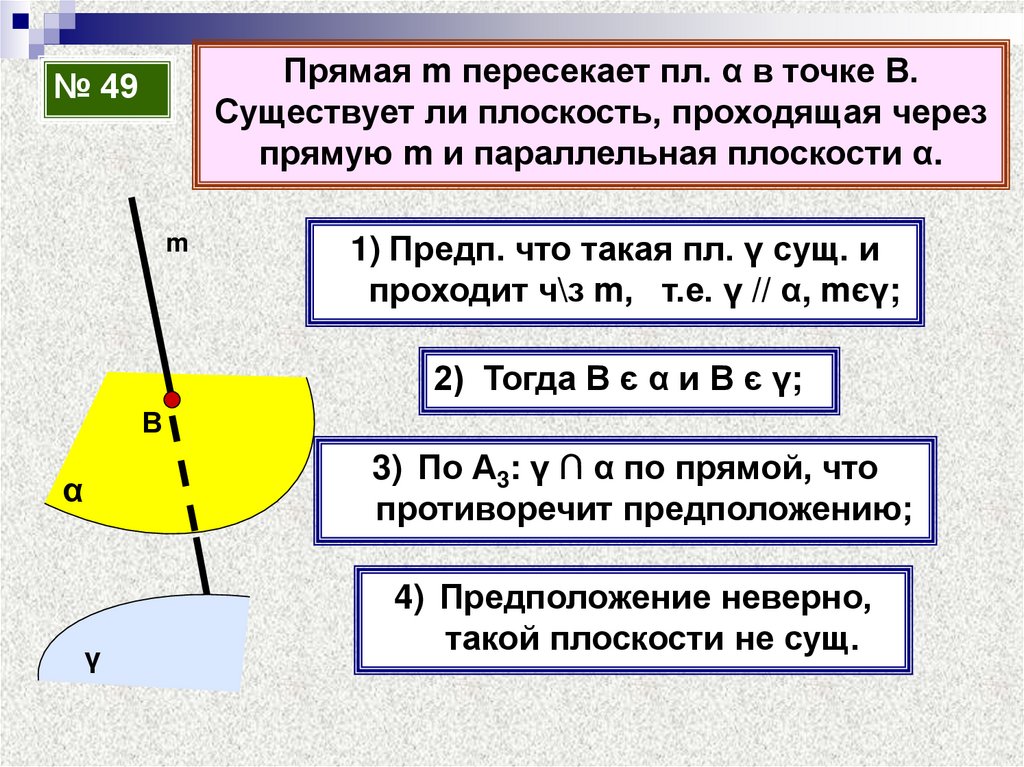
Прямая m пересекает пл. α в точке В.
Существует ли плоскость, проходящая через
прямую m и параллельная плоскости α.
№ 49
m
1) Предп. что такая пл. γ сущ. и
проходит ч\з m, т.е. γ // α, mєγ;
2) Тогда В є α и В є γ;
В
3) По А3: γ ∩ α по прямой, что
противоречит предположению;
α
γ
4) Предположение неверно,
такой плоскости не сущ.

12.

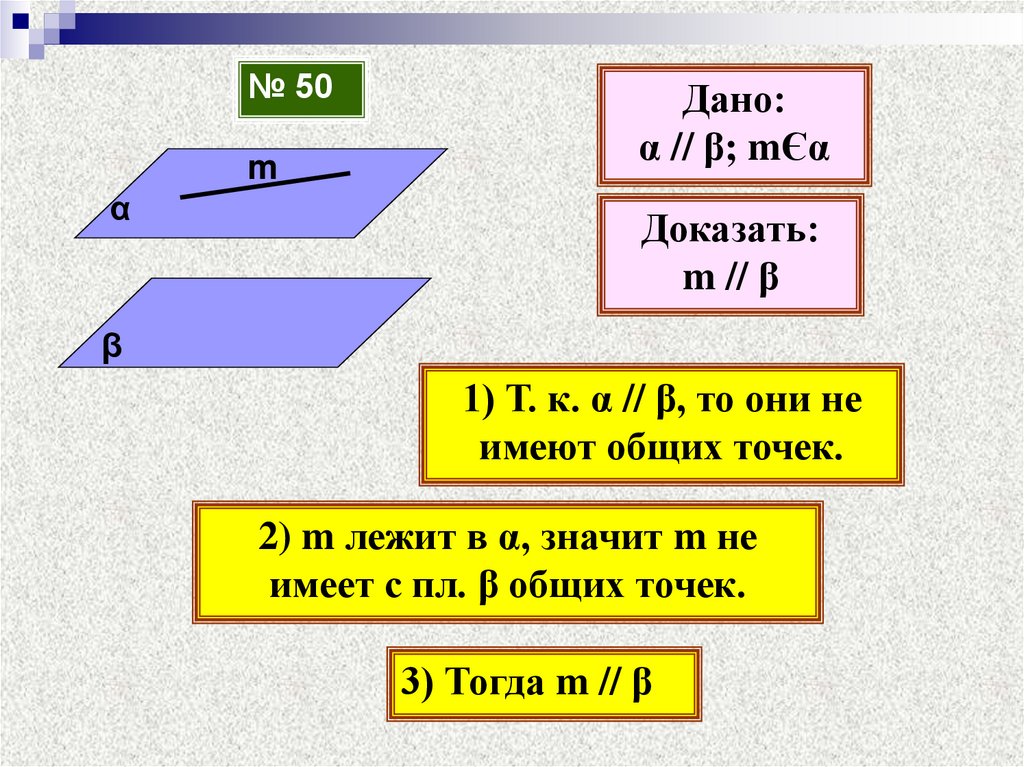
№ 50
m
α
Дано:
α // β; mЄα
Доказать:
m // β
β
1) Т. к. α // β, то они не
имеют общих точек.
2) m лежит в α, значит m не
имеет с пл. β общих точек.
3) Тогда m // β

13.

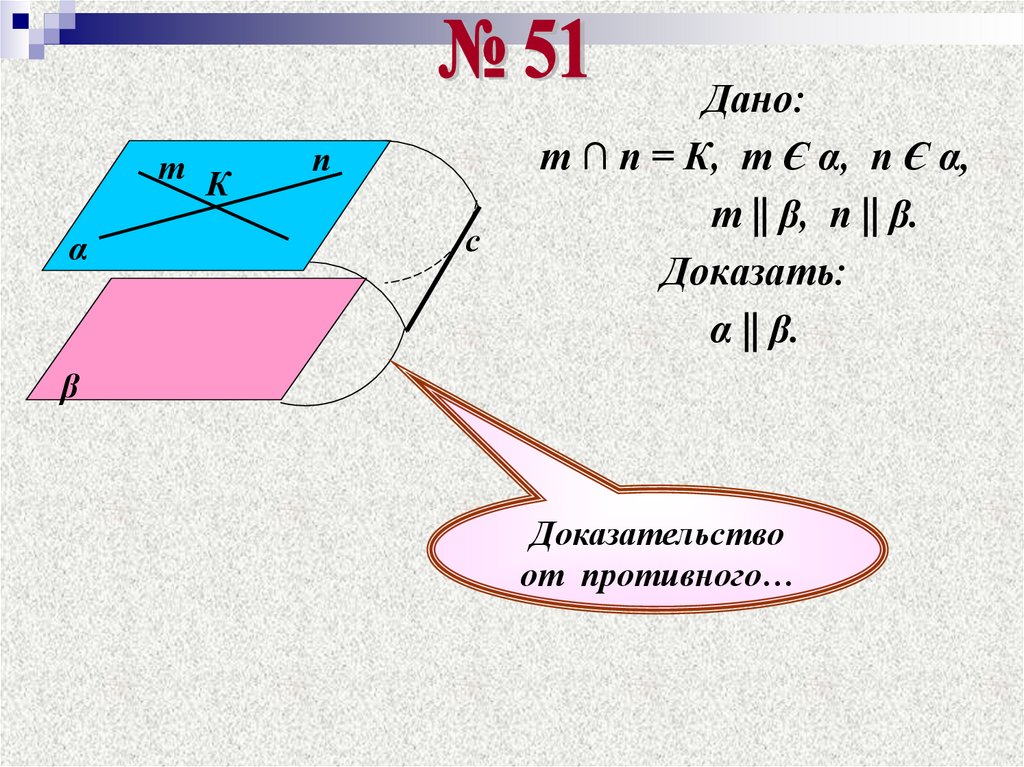
т К
α
п
с
Дано:
т ∩ п = К, т Є α, п Є α,
т || β, п || β.
Доказать:
α || β.
β
Доказательство
от противного…

14.

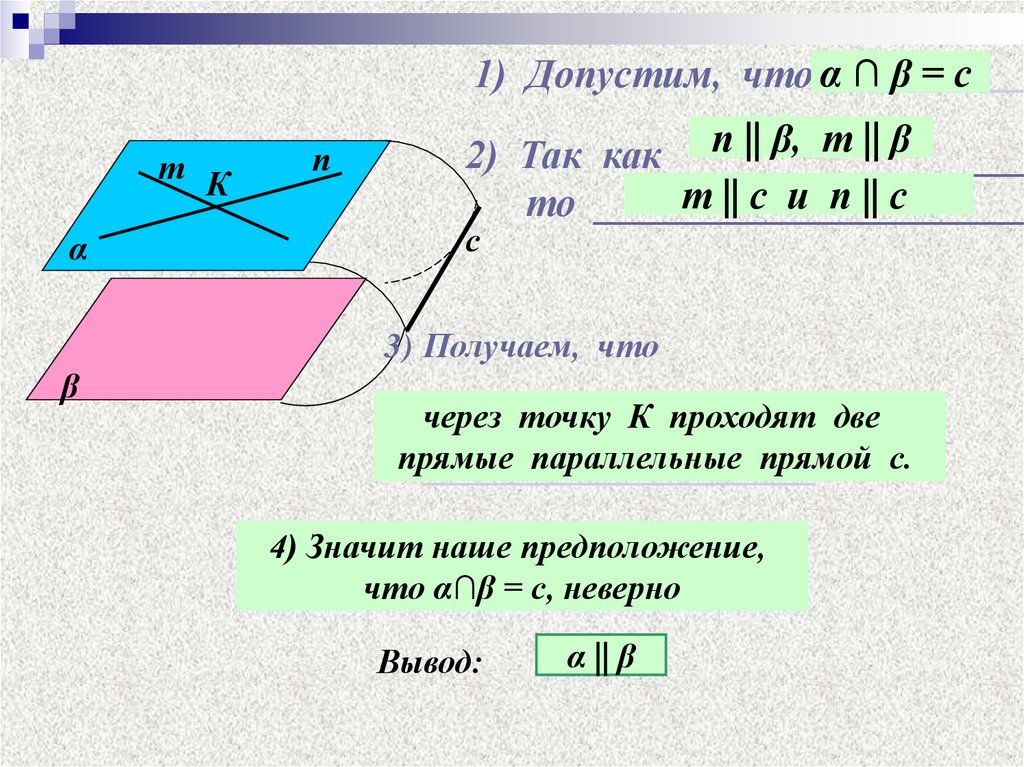
∩β=с
1) Допустим, что α___________
т К
α
п
п || β, т || β
2) Так как __________________
т || с и п || с
то ______________________
с
3) Получаем, что
β
через
точку К проходят две
_______________________________
прямые
параллельные прямой с.
_______________________.
4) Значит наше предположение,
что α∩β = с, неверно
Вывод:
α || β

15.

С1
А1
О
В2
В1
С2
А2
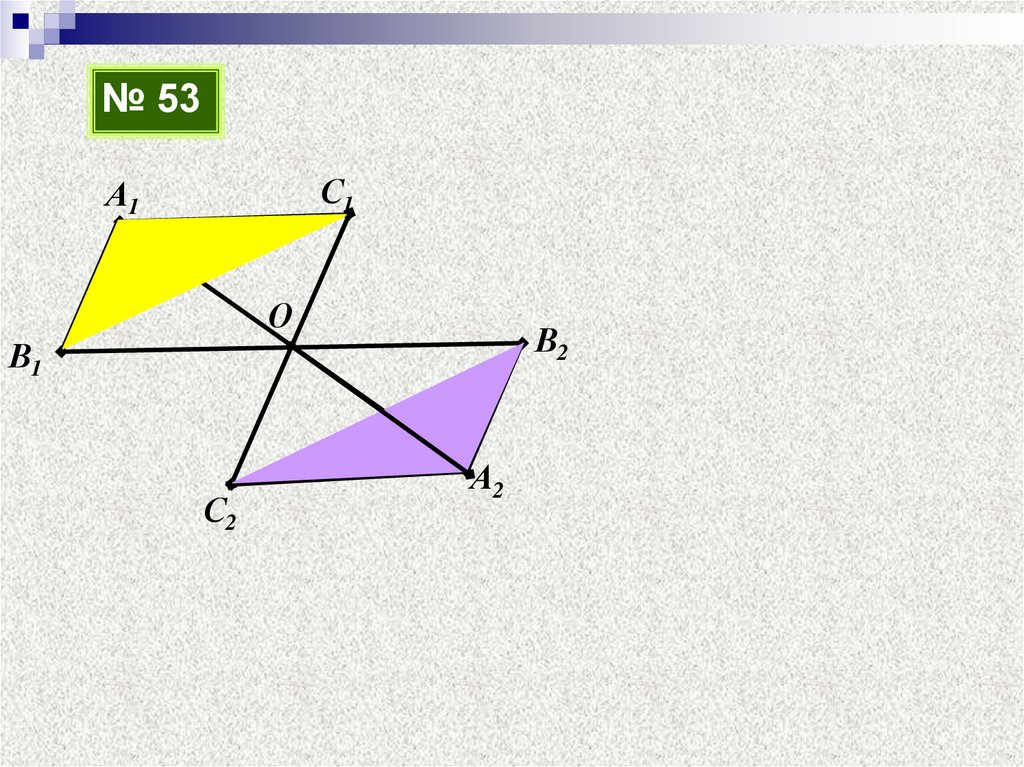
Дано:
отрезки А1А2; В1В2; С1С2
О Є А1А2; О Є В1В2;
О Є С1С2
А1О = ОА2; В1О = ОВ2;
С1О = ОС2
Доказать:
А1В1С1 || А2В2С2

16.

№ 53
С1
А1
О
В2
В1
С2
А2

17.

№ 53
С1
А1
О
В2
В1
С2
А2

18.

В
N
М
C
Р
А
D

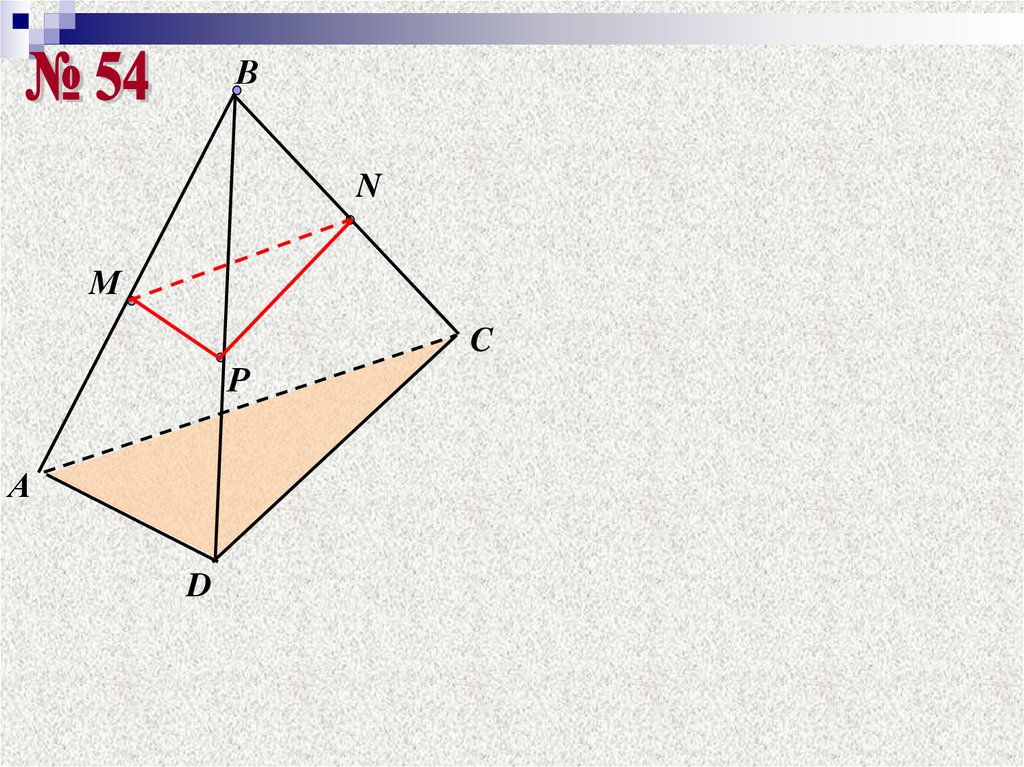
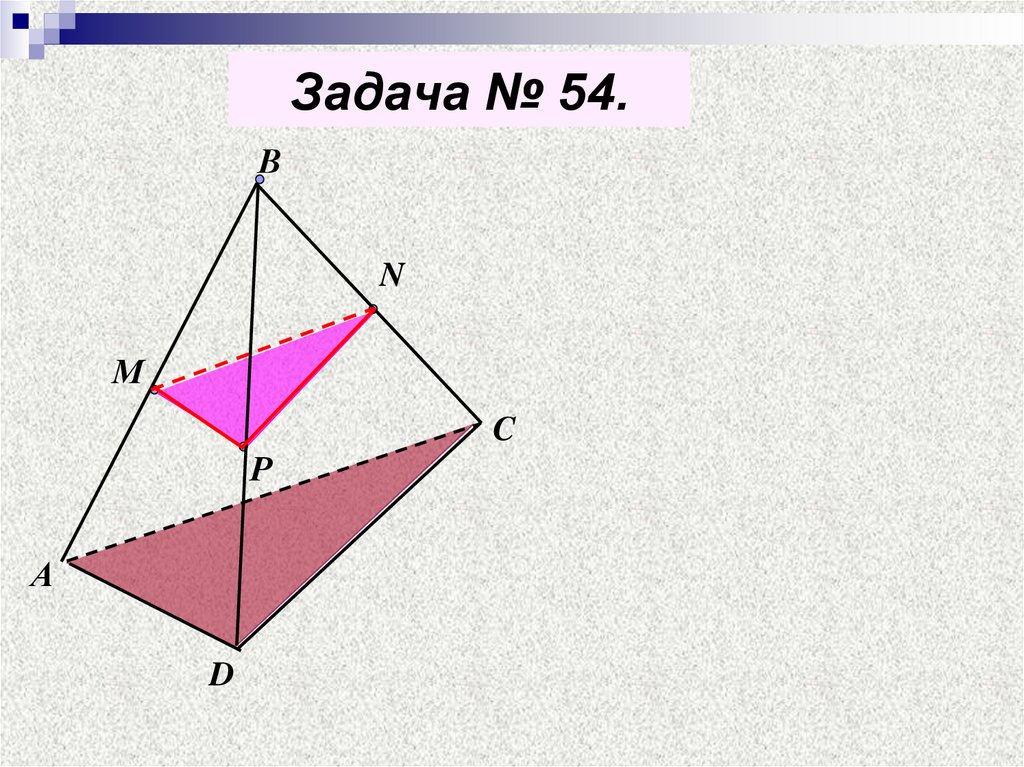
19. Задача № 54.

В
N
М
C
Р
А
D

20.

Да
Нет
Да

21.

Нет
Нет