Проверка адекватности модели

1.

2.

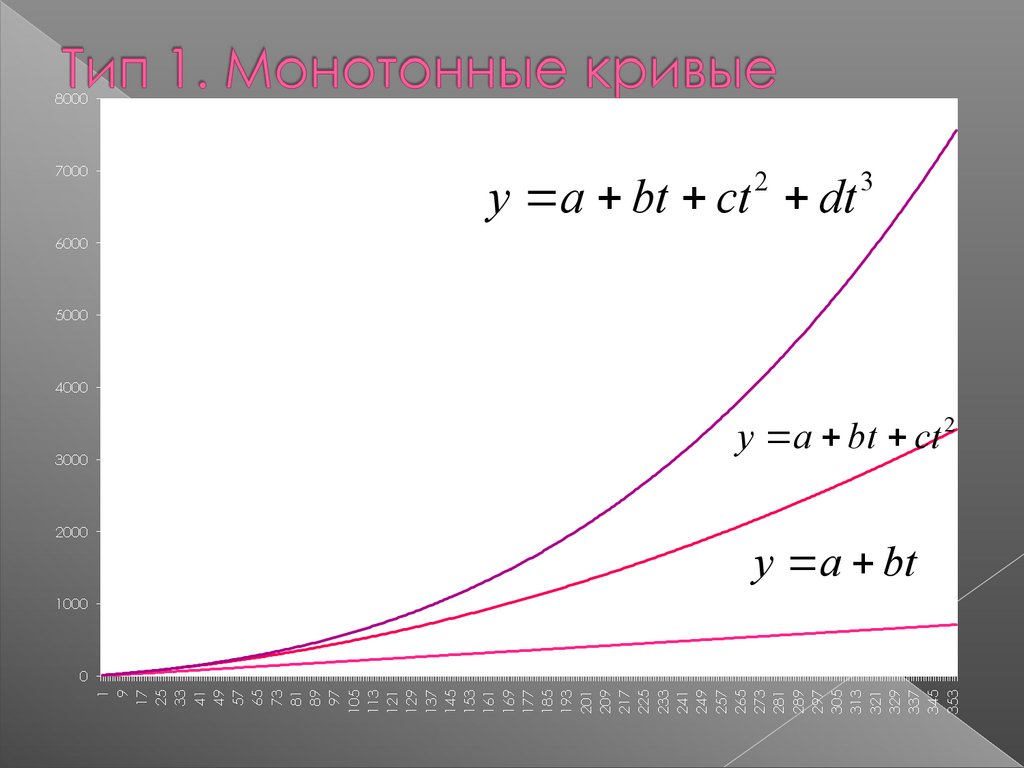
1 Класс – монотонный характер
развития и отсутствие пределов роста
(рост объема производства)
2 класс – «кривые насыщения»
процессы, имеющие предел роста
(потребность в товарах и услугах на
душу населения, демографические
процессы)
3 класс – S-образные кривые
(прогнозирование научно-технического
прогресса, спрос на новый вид
продукции)

3.

2
y a bt ct dt
3
y a bt ct 2
y a bt

4.

y ab
t

5.

6.

1. Выбор одной или нескольких
кривых, соответствующих динамике
временного ряда
2. Оценка параметров выбранных
кривых
3. Проверка адекватности
выбранных кривых прогнозируемому
процессу
4. Расчет точечного и интервальных
прогнозов

7.

Расчет параметров производится
методом наименьших квадратов.
2
~
Q= ( y y )
Данная функция максимизируется

8.

9.

Год
1982
1983
1984
1985
1986
1987
1988
1989
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
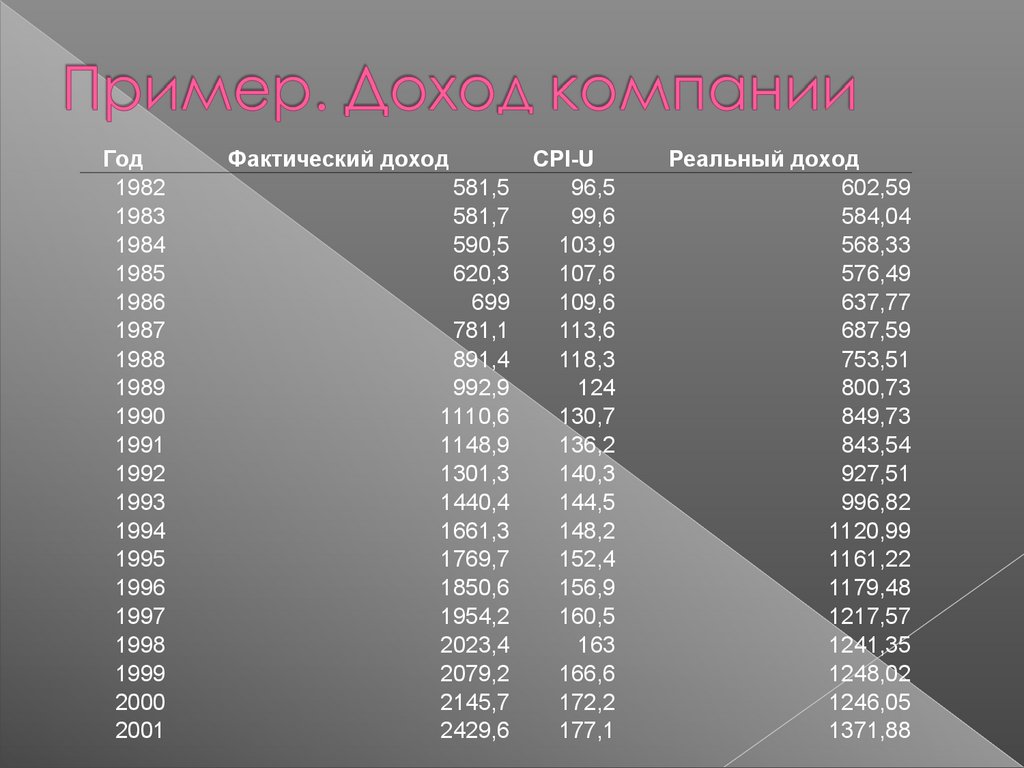
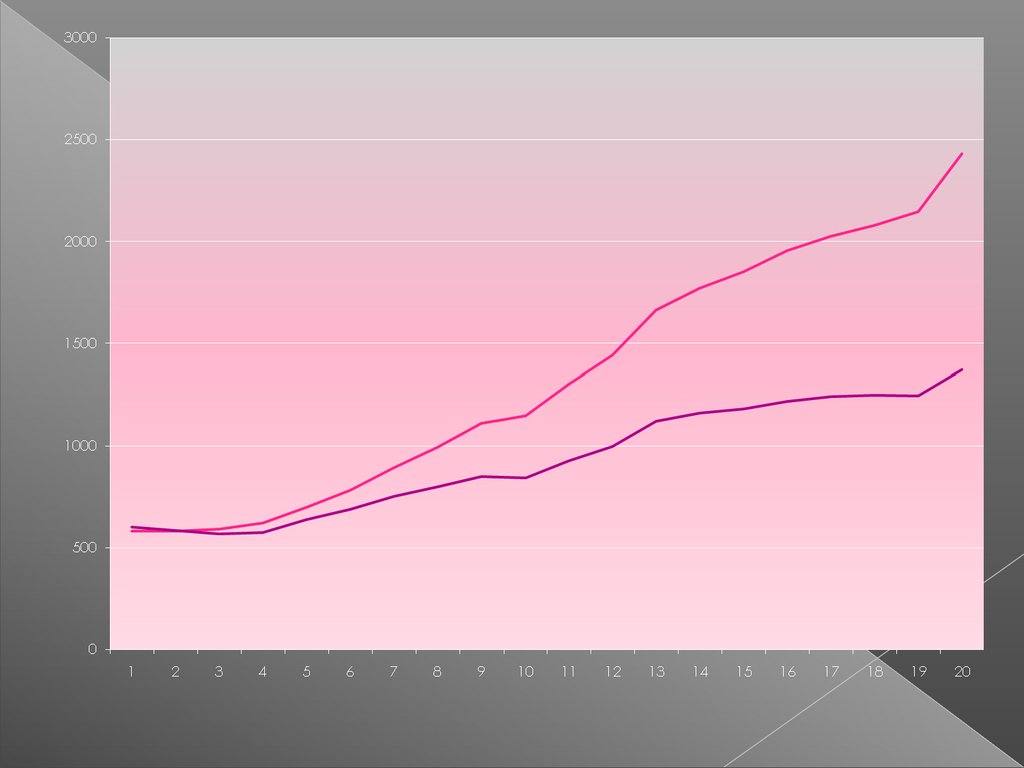
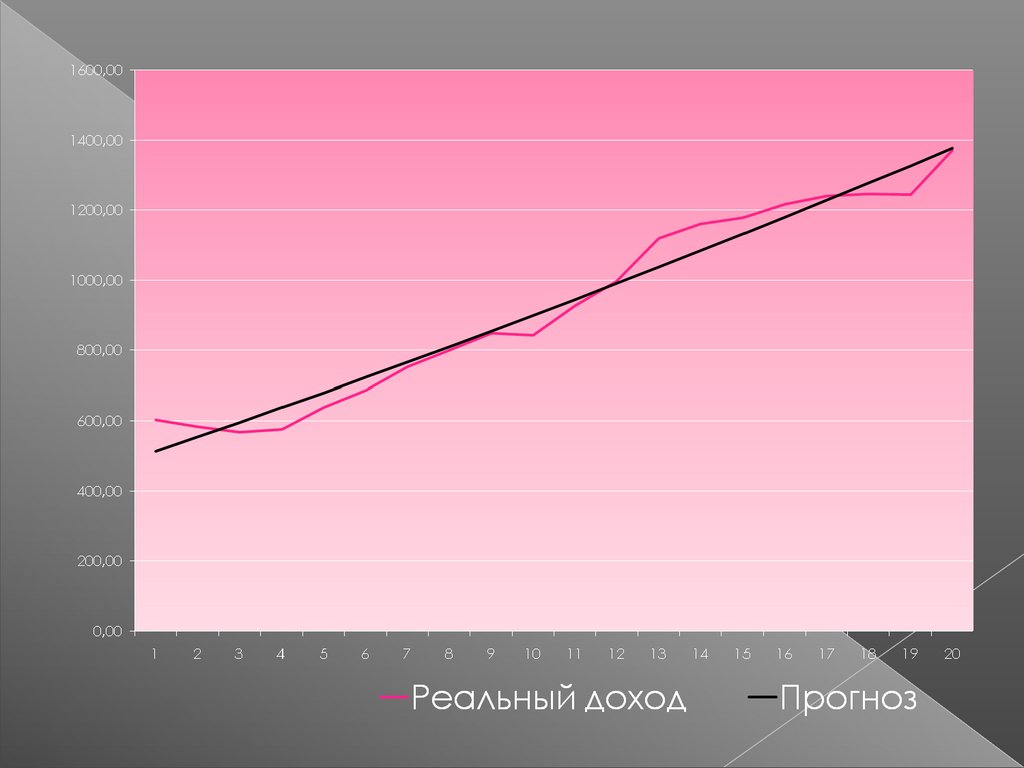
Фактический доход
581,5
581,7
590,5
620,3
699
781,1
891,4
992,9
1110,6
1148,9
1301,3
1440,4
1661,3
1769,7
1850,6
1954,2
2023,4
2079,2
2145,7
2429,6
CPI-U
96,5
99,6
103,9
107,6
109,6
113,6
118,3
124
130,7
136,2
140,3
144,5
148,2
152,4
156,9
160,5
163
166,6
172,2
177,1
Реальный доход
602,59
584,04
568,33
576,49
637,77
687,59
753,51
800,73
849,73
843,54
927,51
996,82
1120,99
1161,22
1179,48
1217,57
1241,35
1248,02
1246,05
1371,88

10.

11.

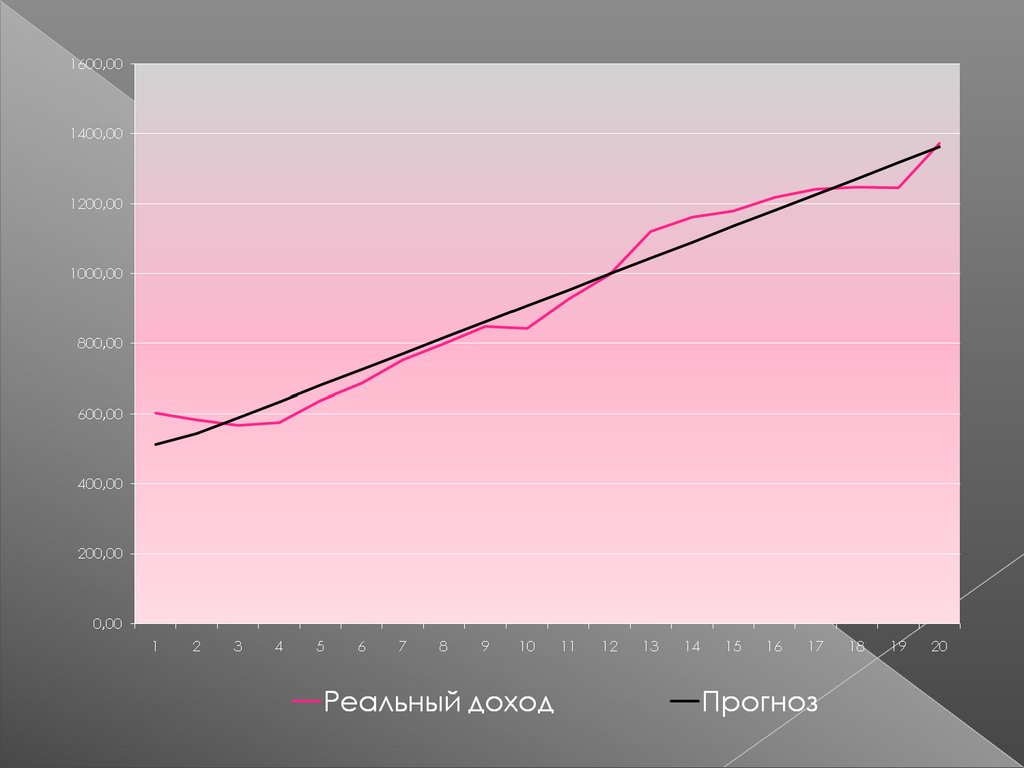
По фактическим данным
рассчитано уравнение
Y=498.656+45.485t

12.

13.

По фактическим данным
рассчитано уравнение
Y=513,052+40.485
2
t+0,253 t

14.

15.

16.

Проверка адекватности выбранной
модели осуществляется на основе
анализа остаточной компоненты.
Пусть ряд содержит только тренд и
случайную компоненту. Ряд остатков
определяется:
et yt yˆ t

17.

Модель
адекватна
описываемому
процессу,
если
ряд
остатков
представляет
собой
случайную
компоненту:
2
N (0, 0 )
, o
M ( t , t )
0 , 0
2
0

18.

Визуальный метод
Критерий Аббе
Метод Фостера-Стюарта
Критерий серий
Критерий Дарбина-Уотсона
И т.д.

19.

Если уравнение кривой подобрано
не верно, то остатки не будут
обладать свойством независимости.
Возникнет автокорреляция остатков

20.

Определение коэффициентов
модели и вычисление остатков.
Расчет статистики Дарбина-Уотсона.
Выбор табличных пороговых
значение в зависимости от уровня
значимости, числа объясняющих
переменных, и числа наблюдений.
Определение области, в которую
попадает вычисленное значение d.

21.

(e e )
d
e
t
t 1
2
t
d 2(1 r1 )
2

22.

Если d близок к нулю, то
существует высокая положительная
автокорреляция.
Если d близок к четырем, то
существует высокая отрицательная
автокорреляция.
Если d близок к двум, то
автокорреляция отсутствует.
На практике рассчитывают верхнее
и нижнее пороговое значение d.

23.

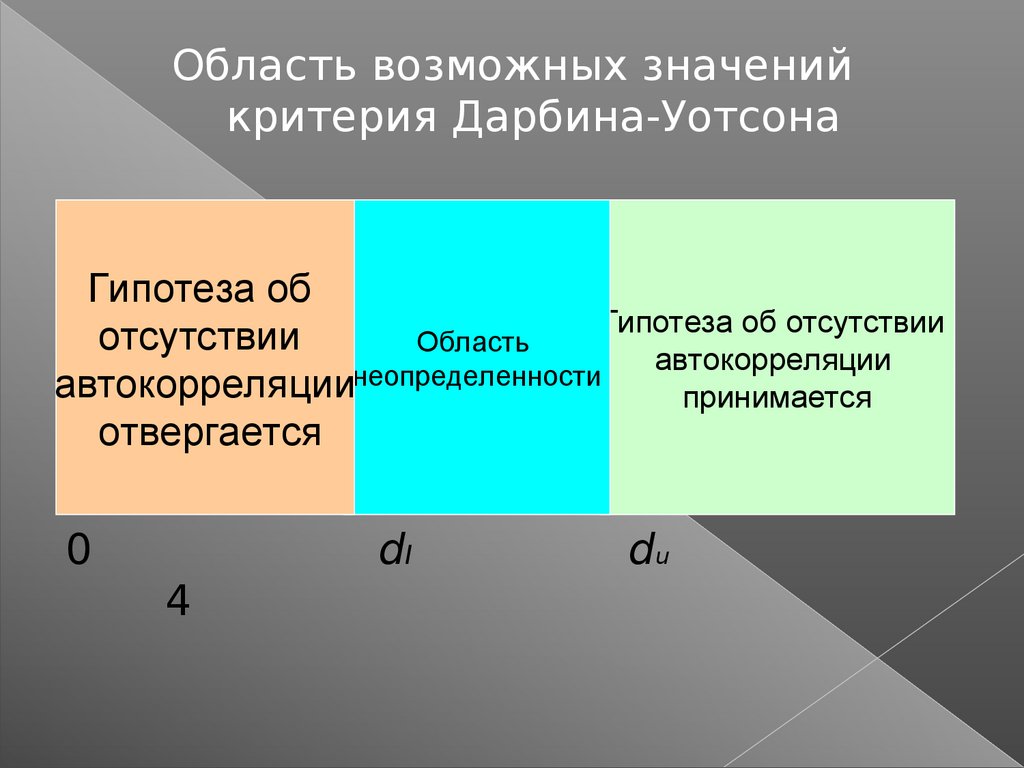
Область возможных значений
критерия Дарбина-Уотсона
Гипотеза об
Гипотеза об отсутствии
отсутствии
Область
автокорреляции
неопределенности
автокорреляции
принимается
отвергается
0
4
dl
du

24.

Ошибка прогноза – разность между
фактическим и прогнозным значение
показателя.
Абсолютная ошибка прогноза:
yˆ t yt

25.

Среднее абсолютное отклонение
| yˆ y |
t
t
n
Относительная ошибка прогноза
yˆ t yt
100%
yy

26.

Средний модуль относительных
ошибок
yˆ t yt
1
100%
n
yy
Используется для сравнения точности
разных объектов прогнозирования.

27.

Средняя квадратическая ошибка
( yˆ y )
S
t
t
2
n
Сумма квадратов ошибок (SSE)
Средние квадраты ошибок (MSE)

28.

Сравнение точности двух
различных методов.
Оценка полезности и
надежности метода.
Поиск оптимального метода.

29.

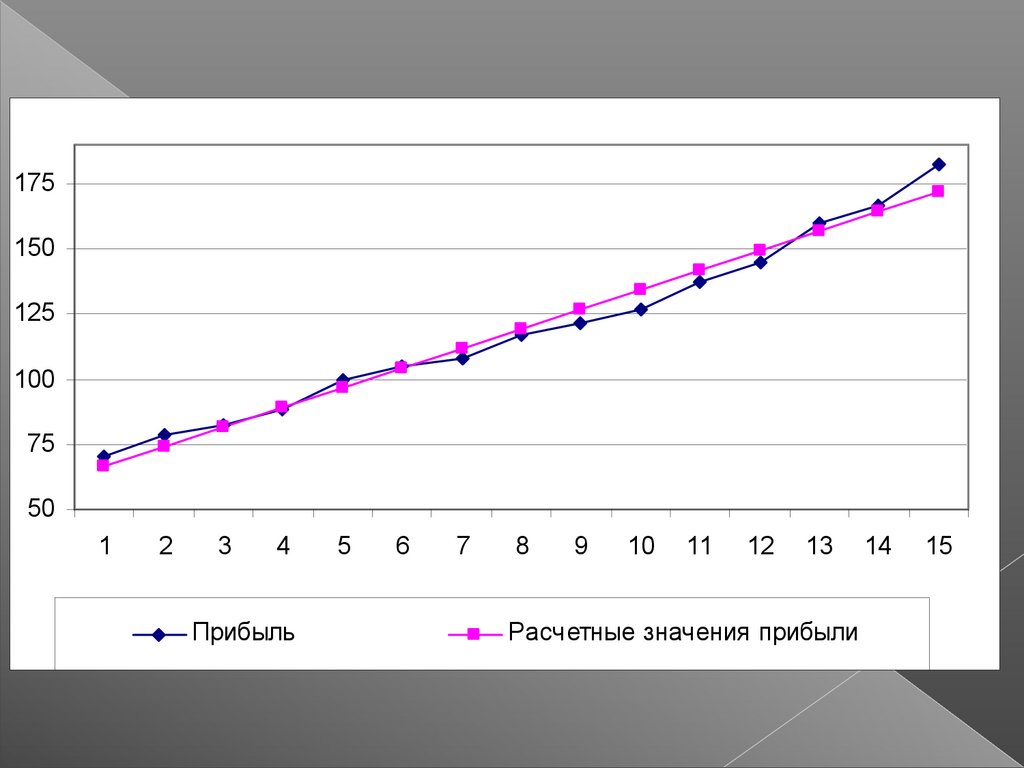
Сравним линейную и
параболическую модель
Рассчитаем для каждой модели
параметры ошибок прогноза

30.

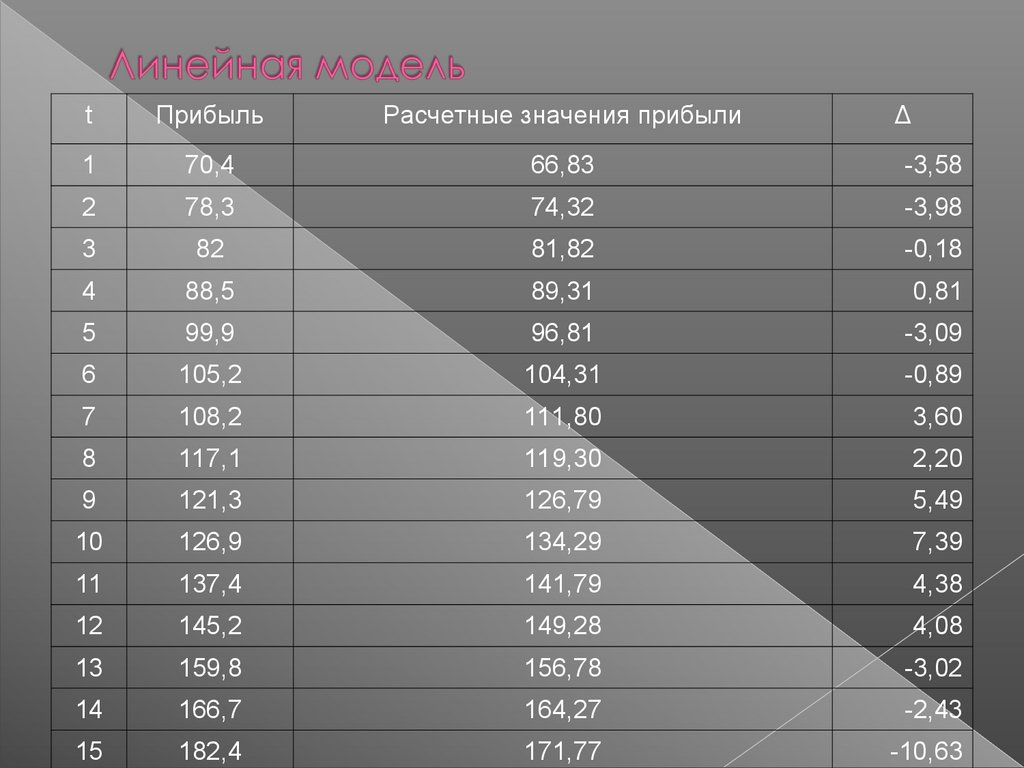
t
Прибыль
Расчетные значения прибыли
Δ
1
70,4
66,83
-3,58
2
78,3
74,32
-3,98
3
82
81,82
-0,18
4
88,5
89,31
0,81
5
99,9
96,81
-3,09
6
105,2
104,31
-0,89
7
108,2
111,80
3,60
8
117,1
119,30
2,20
9
121,3
126,79
5,49
10
126,9
134,29
7,39
11
137,4
141,79
4,38
12
145,2
149,28
4,08
13
159,8
156,78
-3,02
14
166,7
164,27
-2,43
15
182,4
171,77
-10,63

31.

175
150
125
100
75
50
1
2
3
4
Прибыль
5
6
7
8
9
10
11
12
13
Расчетные значения прибыли
14
15

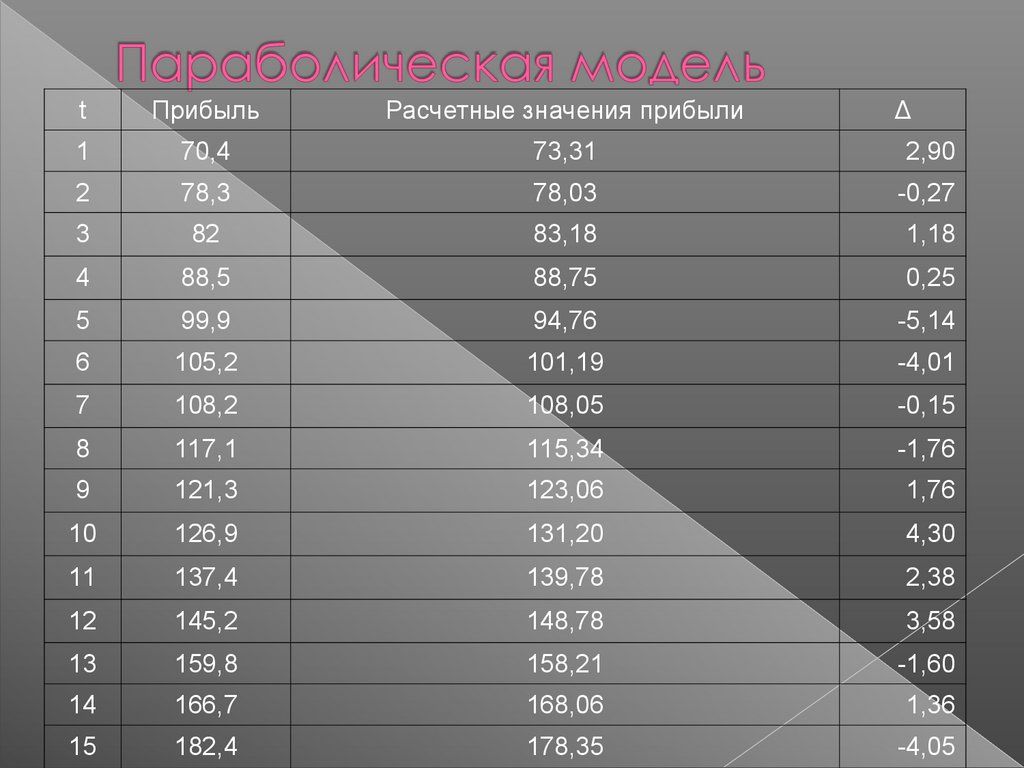
32.

t
Прибыль
Расчетные значения прибыли
Δ
1
70,4
73,31
2,90
2
78,3
78,03
-0,27
3
82
83,18
1,18
4
88,5
88,75
0,25
5
99,9
94,76
-5,14
6
105,2
101,19
-4,01
7
108,2
108,05
-0,15
8
117,1
115,34
-1,76
9
121,3
123,06
1,76
10
126,9
131,20
4,30
11
137,4
139,78
2,38
12
145,2
148,78
3,58
13
159,8
158,21
-1,60
14
166,7
168,06
1,36
15
182,4
178,35
-4,05

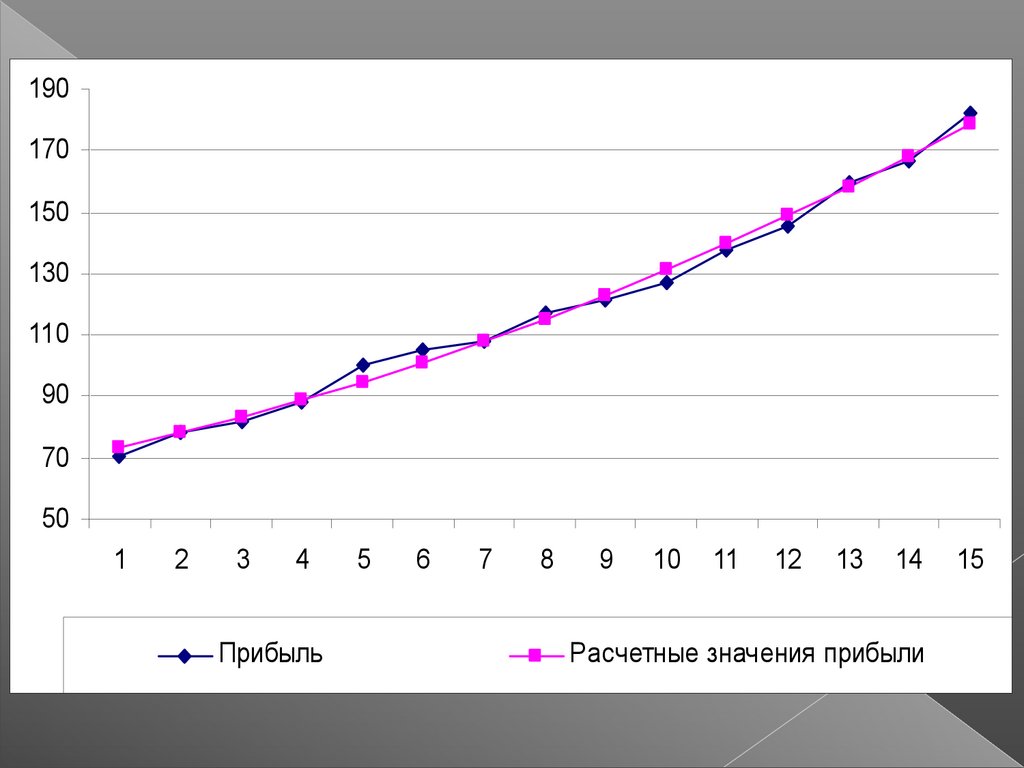
33.

190
170
150
130
110
90
70
50
1
2
3
4
Прибыль
5
6
7
8
9
10
11
12
13
14
Расчетные значения прибыли
15

34.

Линейная модель
Δ = 3.7 тыс. руб.
SSE=304,7 тыс. руб.
MSE=20,51 тыс. руб.
=3.05%
S=4,51 тыс. руб.
Параболическая модель
Δ = 2.32 тыс. руб.
SSE=116,53 тыс.
руб.
=2%
MSE=7,77 тыс. руб.
S=2,79 тыс. руб.

35.

Спасибо за
внимание!