Similar presentations:
Общая химия (лекция 4)
1.
ОБЩАЯ ХИМИЯ(лекция 4)
2.
д.х.н.,профессор
кафедры общей
химии
Конюхов
Валерий
Юрьевич
VK id2476227
3.
План лекций4.
Из программы курса:Основные закономерности
химических процессов
5.
Химическое равновесиеОсновные закономерности химических процессов
Обратимые и необратимые реакции. Химический потенциал и его свойства.
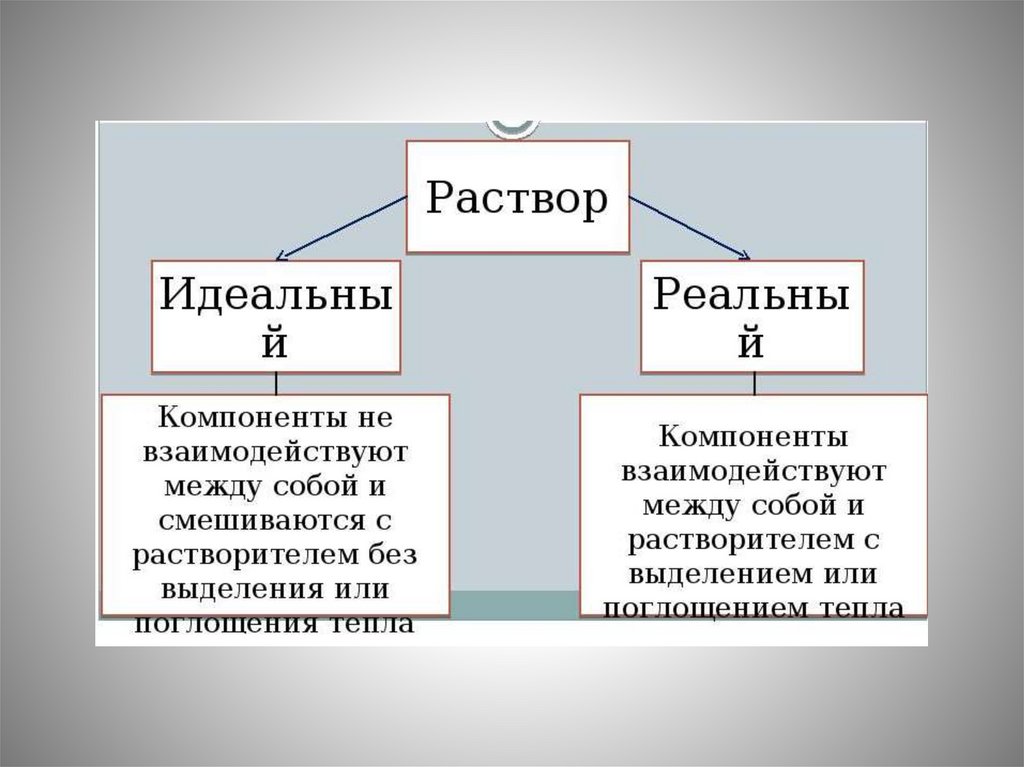
Химический потенциал компонентов идеальных и реальных систем.
Активность и коэффициент активности. Признаки истинного химического
равновесия. Термодинамического условие химического равновесия. Закон
действия масс. Термодинамическая и концентрационная константы
равновесия. Расчет химического равновесия: равновесные концентрации,
степень превращения. Принцип Ле Шателье.
Химическое равновесие в растворах. Сильные и слабые электролиты.
Константа и степень диссоциации слабых электролитов. Закон разбавления
Оствальда.
Гидролиз. Смещение равновесия диссоциации воды в растворах
электролитов. Гидролиз по катиону и аниону: изменение характера среды.
Константа и степень гидролиза.
Химическое равновесие в гетерогенных системах. Константа и коэффициент
распределения. Закон Бертло-Нернста. Произведение растворимости.
6.
Список литературы1. Н.В. Коровин. Общая химия. М.: Высшая школа.
2014.
2. Н.С.Ахметов. Общая и неорганическая химия –
М.:ВШ, 2012.
3. Н.Л. Глинка «Общая химия» М.: Изд. «Химия»,
2002.
4. Жукова Т.В., Глаголева М.А., Липанова Н.В.,
Сергиевский В.В., Сорока И.В. Общая химия
(основные понятия, примеры, задачи). М.: МИФИ,
2008.
5. Сергиевский В.В., Ананьева Е.А., Жукова Т.В.,
Звончевская М.Ф., Кучук Ж.С., Котыхова О.А.
Неорганическая химия: учебное пособие для
внеаудиторной работы. М.: МИФИ, 2007.
7.
ЛитератураОбщая химия лабораторные работы
(под редакцией Е.А. Ананьевой) М.:
МИФИ, 2010.
Сборник тестов и задач по курсу
химии. НИЯУ МИФИ. М.: 2014.
Общая и неорганическая химия (под
редакцией А.Ф. Воробьева).
Т. 1 и 2. М.: Академкнига. 2004.
8.
Химическое равновесие9.
Химический потенциал10.
1. Открытые системы, химическийпотенциал
Системы, в которых протекают химические
реакции (колбы, пробирки и т.п.) являются
открытыми системами. Действительно при
протекании химических реакций одни
вещества превращаются в другие. Количества
веществ в системе изменяются.
Открытые системы – системы, способные
обмениваться друг с другом и окружающей
средой веществом и энергией.
11.
Характеристические функции: G, U, H,S и т.п. величины экстенсивные, т.е.
их величины зависят от количества
вещества в системе, и поэтому они
должны изменятся при протекании
химических или физико-химических
процессов даже при постоянстве Р, Т
(для G).
12.
Следовательно, выведенные намивыражения для dG и т.п. должны
быть дополнены слагаемыми,
учитывающими изменения
количества веществ.
13.
Для однокомпонентной системы:dG SdT VdР μ dn
- химический потенциал,
dn – изменение количества вещества
14.
Для многокомпонентной системы:dG SdT VdP 1dn1
2 dn2 ... n dnn
SdT VdP i dni
i
15.
Для обратимых (квазистатических)процессов:
dG SdT VdP μ i dni
i
Из свойств полного дифференциала dG
вытекает, что химический потенциал i-го
компонента системы i при данном её
составе и постоянстве Р и Т:
G
i
ni P ,T ,n j
16.
Таким образом, с одной стороны,химический потенциал компонента
– это частная производная энергии
Гиббса по количеству (числу моль)
этого компонента ni при постоянстве
Р, Т и количеств других
компонентов nj (т.е. при данном
составе системы)
17.
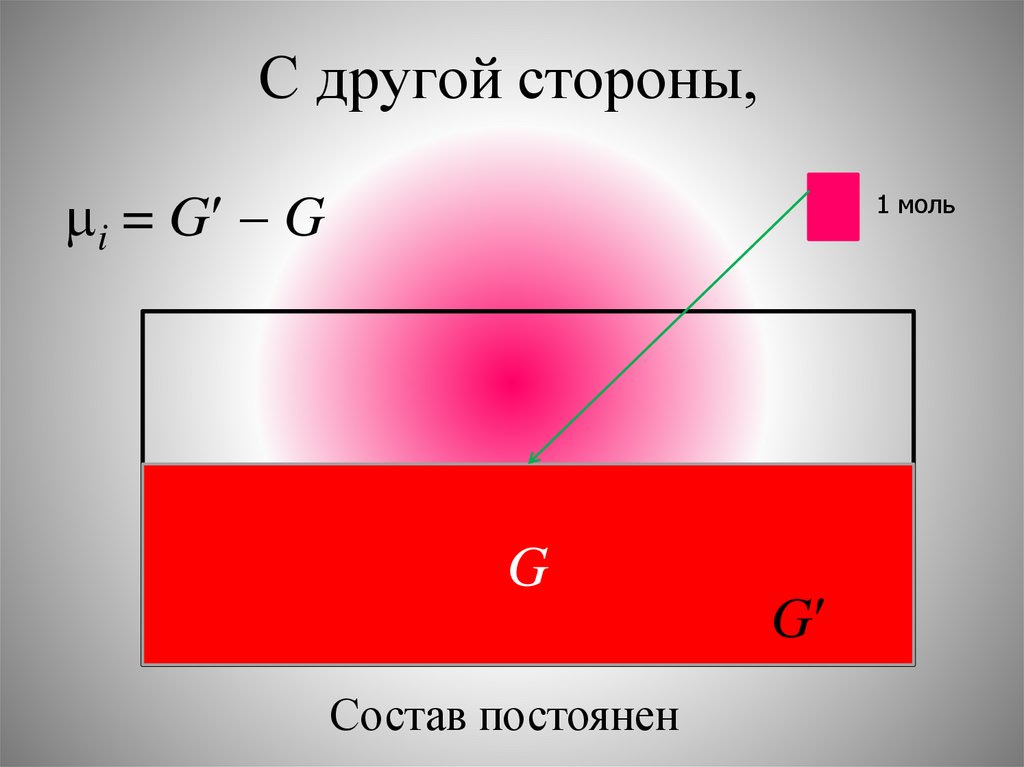
С другой стороны,i = G G
1 моль
G
G
Состав постоянен
18.
химический потенциал компонентачисленно равен увеличению энергии
Гиббса при добавлении в бесконечно
большую систему (настолько большую,
что прибавление 1 моль вещества не
изменяет её состав) одного моль
компонента при постоянных Р и Т.
19.
Для чистого веществахимический потенциал равен
его мольной энергии Гиббса
= Gm
20.
Для идеального газа можнозаписать:
Gm RT ln P
0
Для реального газа:
Gm RT ln f
0
f – летучесть, фугитивность компонента
21.
Для каждого i –го газа смеси идеальныхгазов:
0
i
i
i
RT ln P
Pi – парциальное давление i-го газа
Для каждого i –го газа смеси реальных
газов:
i RT ln f i
0
i
fi – парциальная летучесть i-го газа
22.
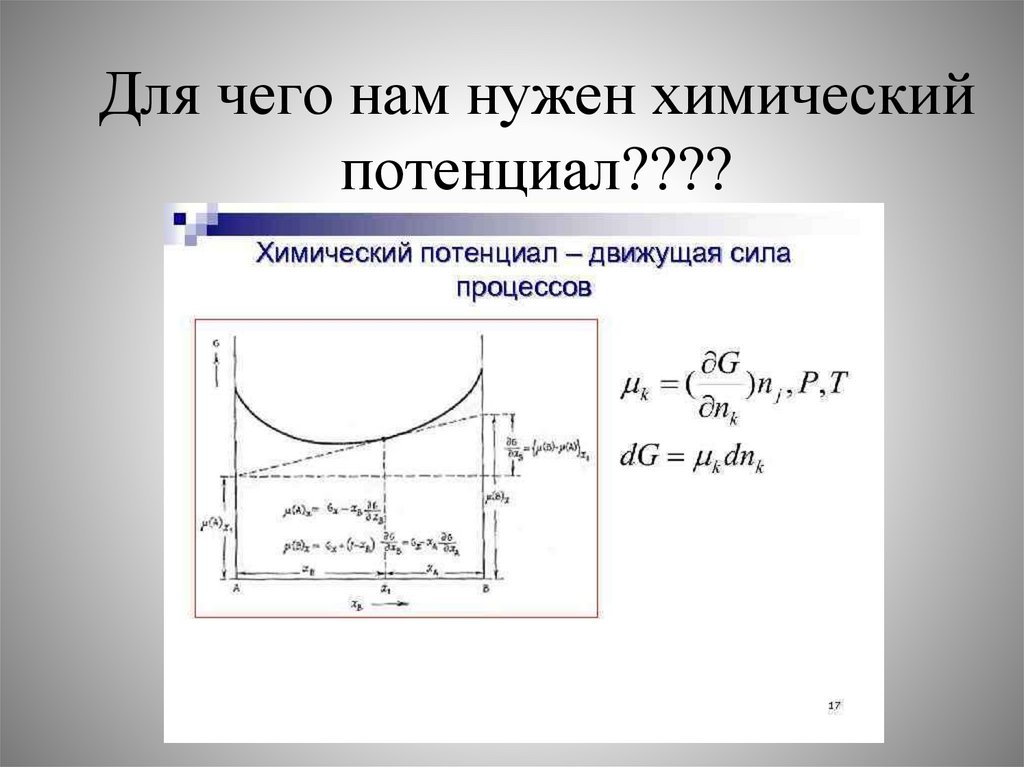
Для чего нам нужен химическийпотенциал????
23.
Все процессы текут в сторонувыравнивания соответствующего
потенциала: так, электрический
ток – от большего потенциала к
меньшему, тепловая (внутренняя)
энергия от тела с большей
температурой к телу с меньшей Т
и т.д..
24.
Все химические и физико-химическиепроцессы протекают в сторону
уменьшения химического потенциала
до тех пор, пока химический
потенциал каждого компонента, в
каждой точке системы не станет
одинаковым.
25.
Это положение принципповсеместного равенства
химического потенциала
26.
Так, если жидкость(однокомпонентная система)
находится в равновесии со своим
паром, то химический потенциал
один и тот же во всех точках
жидкости и по всему объёму
пара.
27.
Если же химический потенциалпара больше химического
потенциала контактирующей с ним
жидкости, то будет идти процесс
конденсации пара до тех пор, пока
химические потенциалы фаз не
сравняются: п = ж
28.
Для многокомпонентнойсистемы, состоящей из Ф фаз и
содержащей К компонентов в
состоянии равновесия:
1
2
3
Ф
1 1 1 .... 1
....
1
2
2
2
3
2
Ф
2
................................
1
K
2
K
3
K
....
Ф
K
29.
При фазовомравновесии
химический
потенциал
каждого
компонента в
каждой фазе
одинаков.
30.
Условия химическогоравновесия
31.
Попробуем понять, как, используяхимические потенциалы
компонентов, сформулировать
условие равновесия для химической
реакции:
1A1+ 2A2+…= 1 A 1+ 2 A 2 …
32.
Для любознательных (вывод)33.
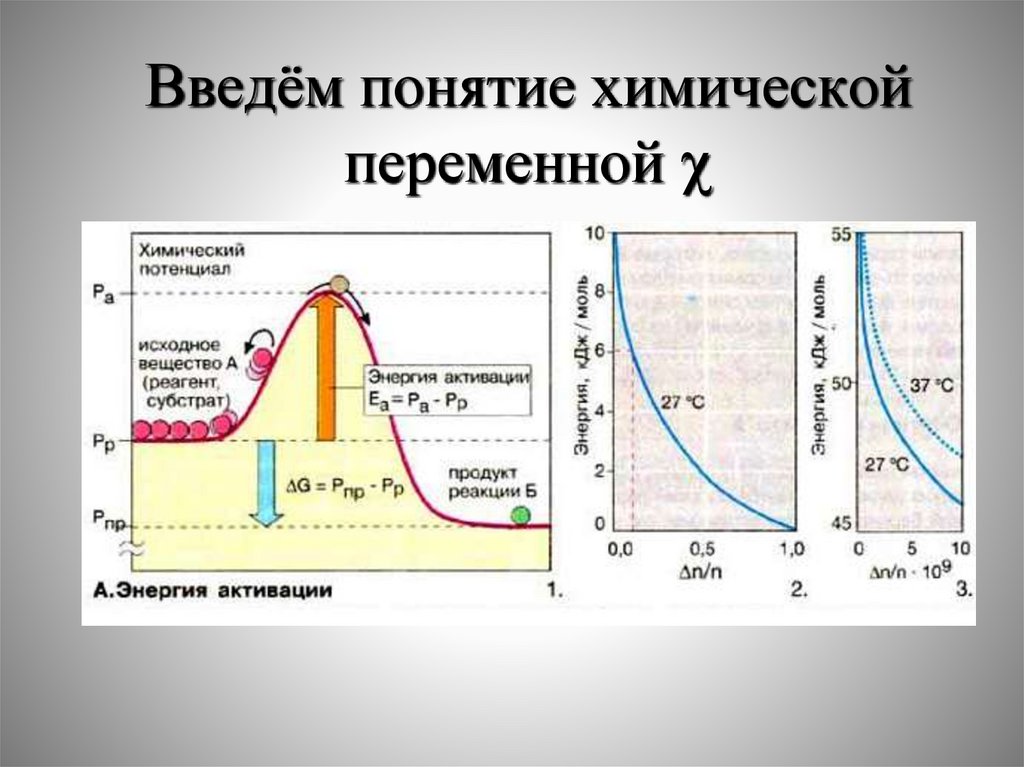
Введём понятие химическойпеременной
34.
Для химической реакции:1A1 2A2+…= 1 A 1 2 A 2 …
dn1 dn2
dn1 dn2
...
... d
1 2
1 2
химическая переменная
(пробег реакции)
35.
Новая запись для dG с учётомхимической переменной:
dG SdT VdP ( i i )d
При такой записи энергия Гиббса –
функция трех переменных Р,Т и
36.
При Р и Т = const:dG P,T ( i i )d
37.
Из свойств полного дифференциала dGследует:
G
( i i )
P ,T
38.
В состоянии равновесия,величина G достигает
минимального значения и:
G
( i i ) 0
P,T
39.
Продолжаем лекцию40.
( ) ...i
i
1 1
2
2
3
3
n
1 1 2 2 3 3 .... m m 0
Это и есть условие
равновесия химической
реакции при P и T = const
n
41.
1 1 2 2 3 3 ... n n1 1 2 2 3 3 .... m m
При равновесии сумма химических
потенциалов продуктов реакции равна
сумме химических потенциалов
исходных веществ (с учётом
стехиометрии реакции)
42.
Для реакции протекающейсамопроизвольно при Р и Т = const
dG < 0
и следовательно ( i i) < 0.
Для обратной (несамопроизвольной)
реакции при Р и Т = const
dG > 0 и ( i i) > 0
43.
Резюме:Если сумма химических потенциалов
исходных веществ больше, чем сумма
химических потенциалов продуктов
реакции, то реакция протекает в сторону
продуктов до тех пор, пока их
химические потенциалы не сравняются, и
наоборот, если преобладают химические
потенциалы продуктов, то реакция идёт в
сторону исходных веществ.
44.
Условие химического равновесияс учетом парциальных давлений
компонентов
45.
()
0
ii
Химический потенциал компонента в
смеси:
i RT ln Pi
0
i
Тогда:
(
T
)
RT
ln
P
0
i
i i
0
i
Черта над Р означает, что давление
равновесное.
46.
Первое слагаемое – функциятолько температуры f(T)
47.
Запишем выражение подругому:ln P
i
i
i (T )
0
i
RT
f (T )
48.
Используя свойствологарифмов, преобразуем
выражение:
ln P
i
i
i (T )
0
i
RT
f (T )
49.
Сумма логарифмов равналогарифму произведений
i
ln Pi
i (T )
Обозначим:
i
Pi К Р
0
i
RT
f (T )
Сейчас требуют
обозначать К
50.
Это термодинамическаяконстанта равновесия,
выраженная через давления:
1
2
i
P1 P2 Pi
К Р 1 2
i
P1 P2 Pi
где Рi = Pi/P0 относительное,
безразмерное давление.
КР она же К , она же Ка
51.
Окончательно имеем:0
i i (T )
i
ln Pi ln K P
RT
Ka K K P e
0
i io
RT
e
r G RT ln K P
0
r G
RT
0
52.
В общем виде для реальныхгазов:
(a )
i
i
1
2
n
1
2
m
f1 f 2
fn
0 0 0
f f
f
f1 f 2
fn
0 0 0
f f
f
Ka
53.
Что мы знаем о химическомравновесии?
54.
Все химические реакции (и физико-химические процессы) идут к состоянию
равновесия, при этом концентрации С
(или Р) реагентов стремятся к
равновесным значениям С (или Р).
Химическое равновесие подвижное.
Положение равновесия в системе зависит
от внешних факторов: температуры,
давления и т.п.
55.
Принцип Ле-ШательеЕсли на систему, находящуюся в
состоянии равновесия, оказывать
внешнее воздействие, то
равновесие в системе изменяется
так, чтобы эффект воздействия
был минимальным.
56.
Например,нагревание
системы, в
которой протекает
экзотермическая
реакция, смещает
равновесие в
сторону исходных
веществ.
57.
Увеличение внешнегодавления смещает
равновесие реакции,
идущей с
уменьшением объёма:
N2 + 3H2 2NH3
в сторону продуктов
реакции и наоборот.
58.
Химическое равновесие. Закондействующих масс
В 1867 Гульдберг и Вааге установили
закон действующих масс, связывающий
равновесные концентрации продуктов
реакции и исходных веществ.
59.
Например, для реакции:1A1 + 2A2 + iAi = 1А 1 + 2А 2 + jА j
в согласии с этим законом можно записать:
KС
C
j
j
i
i
C
KP
j
j
i
i
P
P
Kx
x
j
j
i
i
x
60.
Установим связь между КР, КС и КхДля идеальных газов справедливы
уравнение Клапейрона- Менделеева:
PV = RT = C RT
и уравнение Дальтона:
Рi = P xi
xi – мольная доля i-го газа в смеси,
Р – общее давление смеси.
61.
jKP
Pj
j
(СRT ) j
K
(
RT
)
C
i
i
Pi
(CRT )i
j
KP
( x j P )
i
( xP)
K x ( P)
j i изменение числа
моль газообразных веществ в ходе
реакции.
62.
Если газы реальные, то вместопарциальных давлений используют
равновесные летучести реагентов:
Kf
f
f
j
j
i
i
63.
Если в реакции участвуют вещества вконденсированном состоянии, то в
уравнение подставляют их равновесные
активности аi:
j
Ka
aj
i
ai
64.
Если в реакции участвуют иконденсированные фазы и
реальные газы, то имеют дело с
константой равновесия:
K f ,a
j
j
i
i
f j aj
f i ai
65.
Изотерма химической реакции(изотерма Вант-Гоффа)
66.
Вычислим для реакции:1А1+ 2А2+ iAi 1A 1+ 2A 2+ jA j
изменение энергии Гиббса rG:
rG = jGj(A j ) iGi(Ai)
(1)
67.
Будем считать, что все участникиреакции – идеальные газы.
Энергия Гиббса идеального газа
равна:
Gi = G0i + RT lnPi
(2)
68.
Подставив выражения (2) для каждогоучастника реакции в уравнение (1) и
перегруппировав слагаемые, получим:
0
0
r G j G j i Gi
j
i
RT ln P RT ln P
j
j
j
i
i
i
r G RT ln
0
j
j
i
i
P
P
69.
Здесь Р – относительное(отнесённое к 1 атм), а потому
безразмерное давление.
G0 – стандартная энергия Гиббса
(для идеального газа это состояние
при Р = 1 атм).
70.
rG0 – стандартная энергия Гиббсареакции
Это - разница энергии Гиббса
продуктов и исходных веществ при
условии, что парциальное давление
каждого участника реакции Р = 1
атм.
71.
Pj - парциальные давленияпродуктов реакции в исходной
(взятой для реакции) смеси,
Рi – парциальные давления
реагентов в исходной смеси.
72.
При равновесии rG = 0, тогдаr G r G RT ln
0
или
j
j
i
i
P
0
P
j
r G RT ln
0
Pj
Pi
i
r G RT ln K P (3)
0
73.
Это уравнения изотермы химическойреакции или изотермы Вант-Гоффа
74.
r G r G RT ln0
j
j
i
i
P
P
или
r G RT ln K P RT ln
j
j
i
i
P
P
75.
Для реакции синтеза аммиака:N2 + 3H2 = NH3
Р NH 3
r G RT ln K P RT ln 1 3
PN 2 PH 2
2
где
KP
Р
2
NH 3
1
N2
P
P
3
H2
76.
Для любознательных77.
Поговорим о химическомсродстве:
r G RT ln K P RT ln
Pj
j
i
i
P
При Р и Т = const G = -W max
т.е. равна максимальной полезной работе,
которую способна произвести реагирующая
система при термодинамически обратимом
проведении реакции при Р и Т = const.
Иными словами, это работа, совершаемая
«силой», заставляющей вещества химически
взаимодействовать друг с другом.
78.
Эту «силу» называют –химическим сродством (Я. ВантГофф, 1883 г.) .
Положительный знак сродства
( rG) свидетельствует о
возможности протекания реакции и
наоборот.
79.
Величина и знак ( rG0) определяютсяприродой реагирующих веществ и
температурой. Каждой температуре
соответствует единственное значение
rG0.
Оно равно разности стандартных
химических потенциалов (молярных
энергий Гиббса) веществ, участвующих в
реакции при заданной температуре и
давлении 1 атм.
80.
Второе слагаемое при заданнойтемпературе может приобретать
любые значения (как по величине,
так и по знаку) в зависимости от
соотношения исходных
парциальных давлений (или
активностей) участников реакции.
81.
Для каждой реакции существуетбесконечное множество значений
RT lnПРi определяемых общим
давлением газовой смеси и ее
составом, но только одно из них
отвечает составу равновесной смеси,
при котором химическое сродство и
изменение энергии Гиббса равны нулю
rG = 0
82.
И снова лекция:Зависимость константы
равновесия от температуры.
Изобара химической реакции
(изобара Вант-Гоффа)
83.
Известно дифференциальноеуравнение Гиббса - Гельмгольца,
связывающее rG с температурой:
r G
r H
T T
2
T
P
84.
Подставив в него уравнение (3):r G RT ln K P
0
получаем:
d ln K p
dT
r H
2
RT
0
85.
Это уравнение изобары ВантГоффа в дифференциальной
форме
Оно связывает константу равновесия КР
реакции с её тепловым эффектом rН0
(при Р = const) и температурой.
86.
Полученное уравнение изобарыпозволяет предсказать
направление смещения равновесия
при изменении температуры в
зависимости от знака теплового
эффекта реакции ( rН).
87.
Если реакция экзотермическая( rН < 0), то с увеличением температуры
КР или КС уменьшаются, в согласии с
принципом Ле Шателье.
Таким образом, изобара Вант-Гоффа
являются теоретическим обоснованием
эмпирического принципа Ле-Шателье.
88.
Изобара Вант-Гоффа винтегральной форме
89.
Интегрирование полученныхдифференциальных уравнений при
условии rН = const или
rU = const даёт:
r H
ln K P
const
RT
0
rU
ln K C
const
RT
0
90.
r Hln K P
const
RT
0
Сравним его с уравнением:
RT ln K P r G r H T r S
0
0
r H r S
ln K P
RT
R
0
т.е. в этом случае:
r S
const
R
0
0
0
91.
Определения теплоты реакциииз данных о температурной
зависимости КР
92.
Полученные интегральныеуравнения дают хороший способ
определения теплоты реакции
( rН0 или rU0) без помощи
калориметра.
93.
Для этого измеряют равновесныепарциальные давления или
равновесные концентрации реагентов
при нескольких температурах.
Далее вычисляют КР и полученные
значения располагают в координатах
lnKP от 1/Т
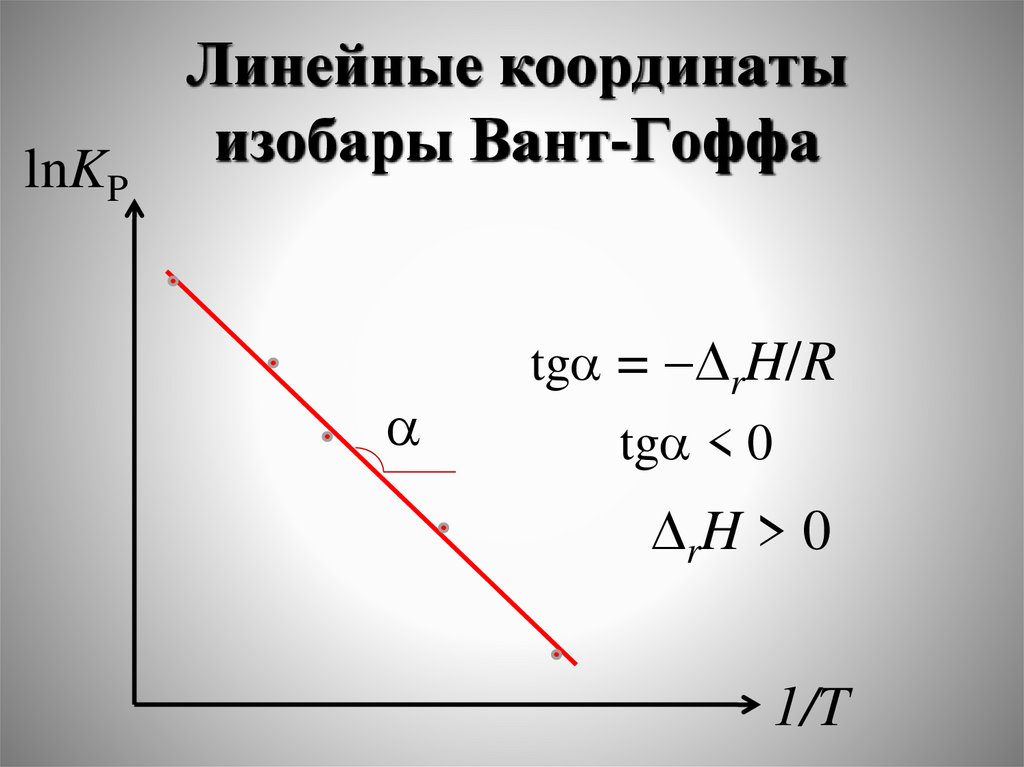
94.
lnKPЛинейные координаты
изобары Вант-Гоффа
a
tga = rH/R
tga < 0
rH > 0
1/T
95.
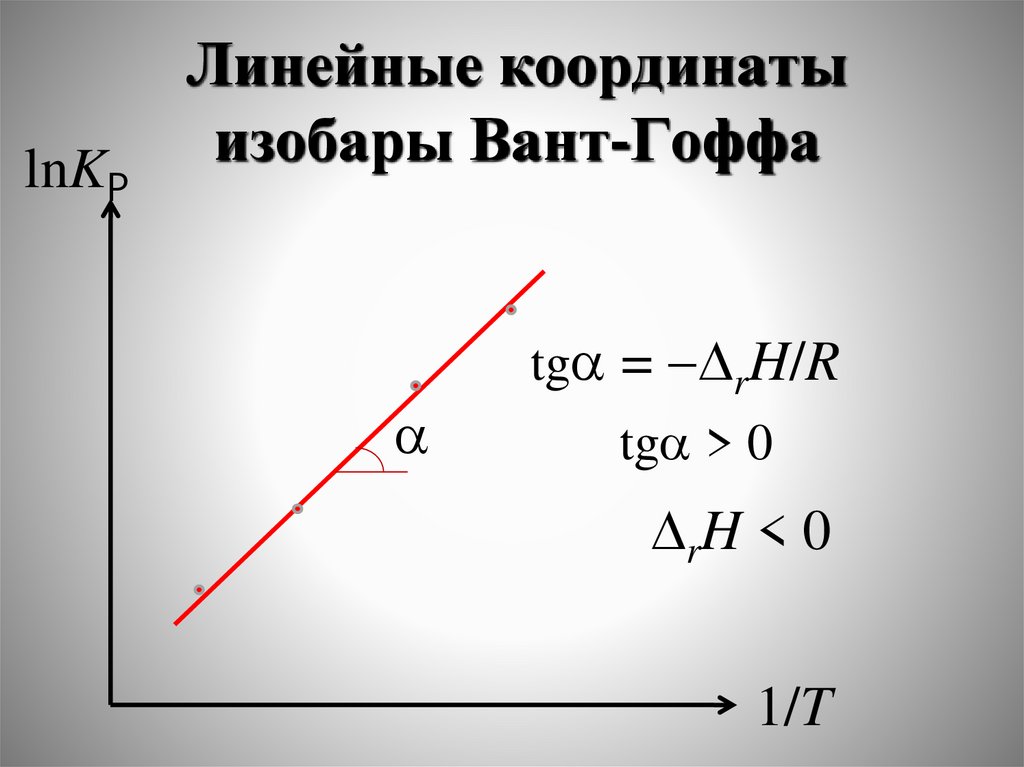
lnKPЛинейные координаты
изобары Вант-Гоффа
a
tga = rH/R
tga > 0
rH < 0
1/T
96.
Для двух значений Т1 и Т2 исоответствующих им КР1 и КР2:
Интегрирование дает при rН = const
(в узком интервале температур):
r H 1 1
ln
K P1
R T1 T2
K P2
0
97.
Для любознательных98.
Если rH ≠ const99.
Если rH0T = rH0298 + rC0P(T – 298), тоинтегрирование изобары Вант-Гоффа
дает:
ln K P
r H
0
298
r С 298
RT
0
Р
rС
ln T const
R
0
Р
100.
И снова лекция101.
Трактовка rG > 0102.
В классической термодинамике фактG > 0 означает, что рассматриваемый
процесс невозможен (он не
самопроизвольный, отрицательный).
Например, невозможен
самопроизвольный переход энергии в
форме теплоты от холодного тела к
более нагретому или
самопроизвольное сжатие газов.
103.
В химической термодинамике факт,что rG > 0 означает лишь то, что
равновесие в системе смещено в
сторону исходных веществ
(произведение равновесных давлений
продуктов меньше по величине, чем
произведение равновесных давлений
исходных веществ).
104.
Вычисление констант равновесияхимических реакций
105.
Для вычисления констант равновесияи равновесных концентраций или
давлений участников реакции
рассчитывают rG0 реакции.
Далее КР или КС вычисляют из
уравнений:
r G RT ln K P
0
r А RT ln K С
0
106.
Вычисление rG0107.
1. rG0298 = rН0298 Т rS0298Величину rН0298 вычисляют через
теплоты образования fН0298 или
теплоты сгорания охН0298веществ.
Величину rS0298 вычисляют по
уравнению:
rS0298 = j S0298(A’j) iS0298(Ai)
108.
2. Вычисление rG0 черезстандартные энергии Гиббса
образования веществ fG0298
109.
Для любознательных110.
3. Вычисление rG0 методомТёмкина-Шварцмана.
0
0
GT0 H 298
T S 298
T ( a M 0 b M 1 c M 2 d M 3 c M 2 )
М1, М2 и т.д. – константы уравнения
Темкина-Шварцмана, их значения
приведены в справочниках (обычно с
интервалом в 100 К)
а, в, с и т.д. – изменение в ходе реакции
эмпирических констант уравнений:
c
C Р a bT
T2
CР a bT cT
2
111.
4. Вычисление констант равновесиячерез приведенные энергии Гиббса Ф:
Этот метод позволяет вычислять
константы равновесия при любой
температуре (с интервалом в 100 К),
минуя расчёт rG0 (табл. 50).
Для этого в справочниках практически
для всех веществ представлены т.н.
приведенные энергии Гиббса - Ф:
112.
Приведенные энергии Гиббса(табл. 50):
G H
Ф
T
0
0
0
r H
1
lg K a ,T
r Ф
4,57
T
0
0
rФ jФ( A j ) iФ( Ai )
или
r H j f H ( A j ) i f H 0 ( Ai )
0
0
0
0
0
r H ai ox H ( Ai ) j ox H 0 ( A j )
0
0
0
0
0
113.
5. Вычисление констант равновесияреакций через константы
равновесия реакций образования
веществ lgKf (табл. 49)
lg K a ,T j lg K f ( A j ) i lg K f ( Ai )
114.
6. Вычисление константравновесия реакций по
эмпирическим уравнениям
(табл. 41).
Например. Для константы равновесия реакции:
2SO2(г) + O2(г) = 2SO3(г)
в табл. 41 приводится эмпирическое уравнение:
3
10679
0
,
354
10
lg K a
0,736 lg T 0,114 10 3 Т
12,419
2
T
T
115.
Равновесия в растворахэлектролитах
116.
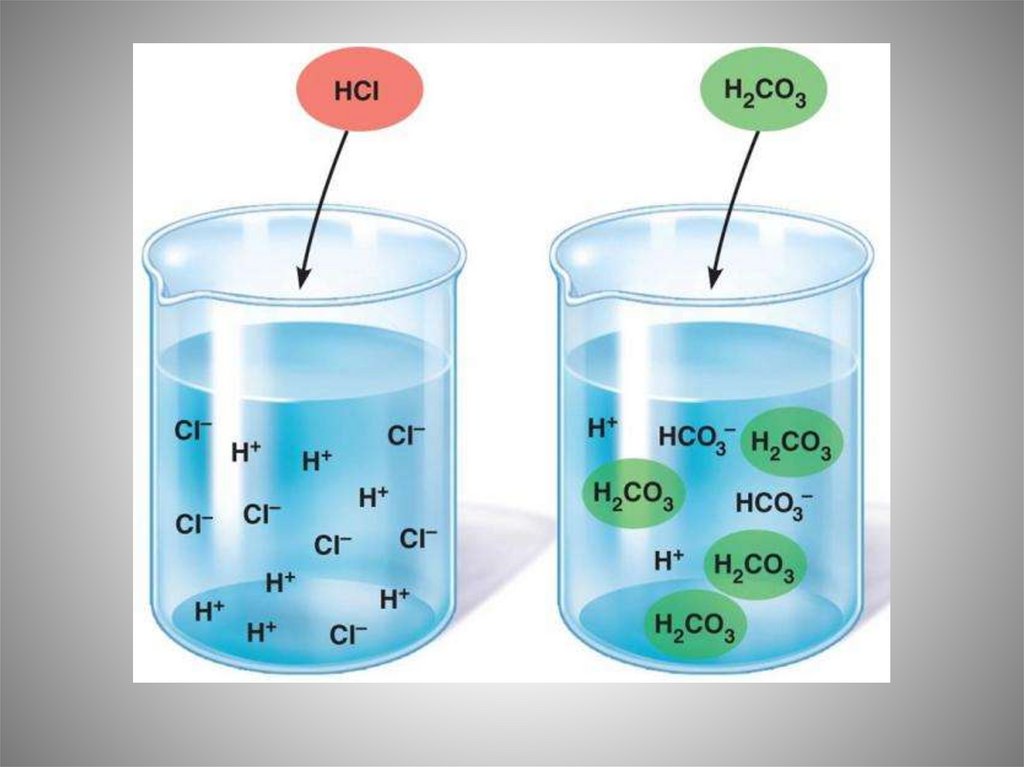
Особенности реакций и равновесия врастворах электролитов
Химические свойства раствора электролита
складываются из свойств образующих его ионов.
Группа электролитов, содержащая один и тот же
вид ионов, обладает сходными химическими
свойствами.
Так, все растворы, содержащие хлорид-ионы Сl ,
при добавлении к ним раствора нитрата серебра
AgNO3 дают белый осадок хлорида серебра AgCl.
Подобные качественные реакции на данный вид
ионов широко используются в аналитической
химии при определении состава растворов.
117.
Основным фактором, влияющим на смещениеравновесия в растворах электролитов, является
изменение концентрации ионов. Поэтому обменные
реакции в растворах идут в сторону малорастворимых
веществ или слабых электролитов.
Это правило легко объяснимо, так как в результате
протекания таких процессов один или несколько
видов ионов выводятся из сферы взаимодействия, что
в соответствии с принципом Ле Шателье должно
привести к более полному протеканию реакции.
Малорастворимые вещества могут выводится из
раствора или в виде осадка, или в виде газа. Слабыми
электролитами могут быть кислоты и основания, вода
и комплексы.
118.
Электролиты бывают сильными ислабыми.
Сильные электролиты диссоциируют
полностью (a = 1) при любой
концентрации.
Слабые электролиты диссоциируют
лишь незначительно и степень их
диссоциации a увеличивается при
разбавлении. При бесконечном
разбавлении, когда С 0 a 1.
119.
120.
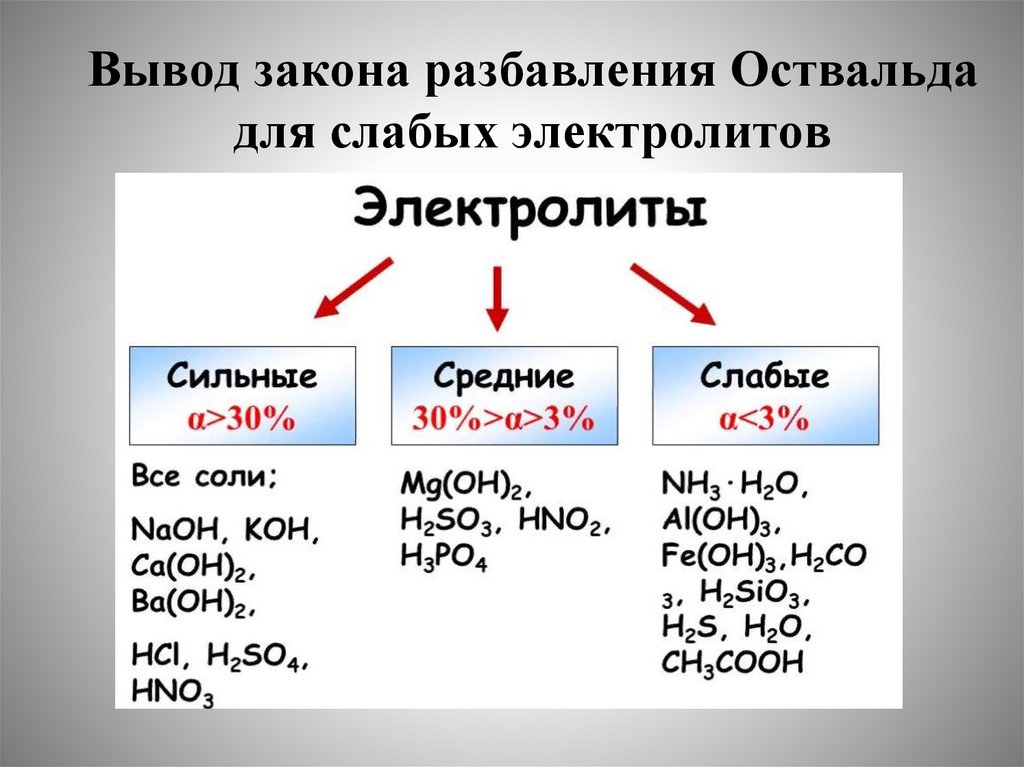
Вывод закона разбавления Оствальдадля слабых электролитов
121.
Пусть слабый электролит АBдиссоциирует в согласии с уравнением:
АB AZ+ + BZ К процессу электролитической
диссоциации применим закон
действующих масс.
Константа равновесия (константа
электролитической диссоциации),
выраженная через концентрации:
C C
KC
Co
122.
Концентрации ионов и молекул врастворе равны:
С+ = a С,
С- = a С,
Следовательно:
Со = С(1 a)
aС aС a С
КC
;
С (1 a ) 1 a
2
V 1/ C
KC
a2
V (1 a )
(1)
Здесь V – разбавление раствора, это такой объем
раствора, который содержит 1 моль растворенного
вещества.
Закон разбавления В. Оствальда
123.
( К 4КC С КC )a
;
2С
При α 1, (тт.е при малых К C
2
C
и достаточно больших С ) :
a
КC
С
Степень диссоциации уменьшается с ростом
концентрации.
124.
Константа диссоциации КС в отличие отстепени диссоциации a не зависит от
концентрации раствора (в определенном
интервале С) и определяется в первую
очередь природой электролита и
растворителя.
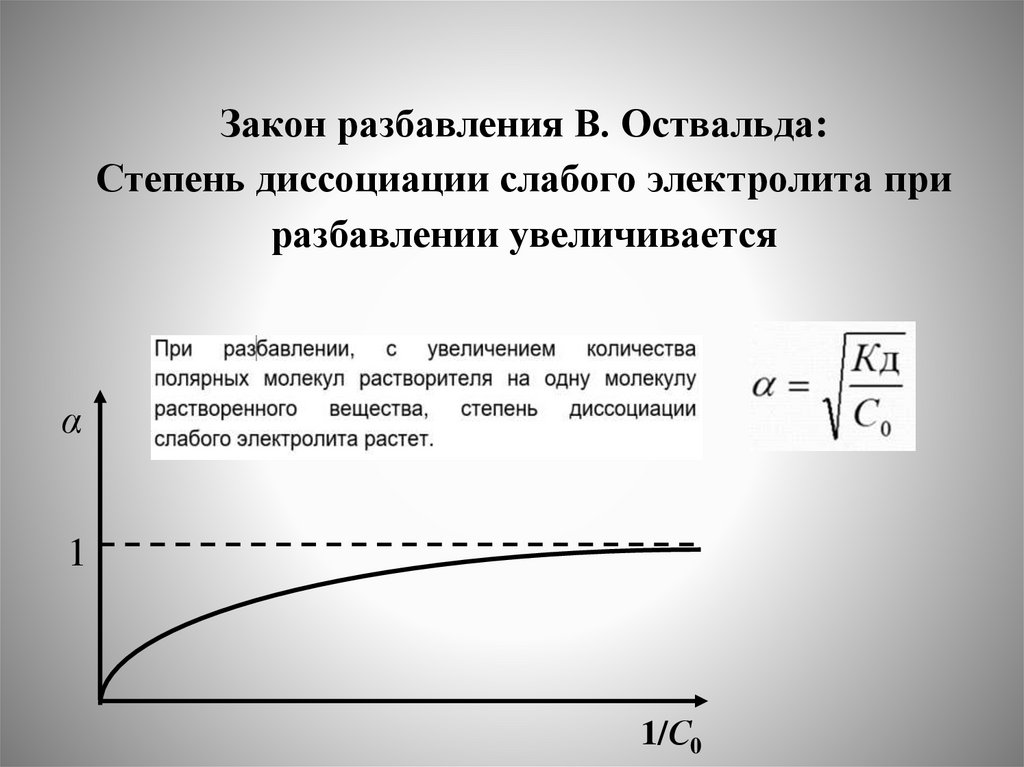
125.
Закон разбавления В. Оствальда:Степень диссоциации слабого электролита при
разбавлении увеличивается
α
1
1/С0
126.
Константы диссоциации слабых кислот иоснований в водных растворах при 25°С
Кислота
К
pK
(I) 3,71 10-5
4,430
(II) 3.87 10-6
5,412
5,56·10-5
4,255
(I) 1,29·10-2
1,990
(II) 1,26·10-4
3,900
6,3 10-5
4,201
(I) 5,83 10-10
9,234
(II) 1,8 10-13
12,745
(III) 1,6·10-14
13,80
m-Бромбензойная С7Н5О2Вг
1,54 10-4
3,812
о-Бромбензойная С7Н5О2Вг
1,40·10-3
2,854
Адипиновая С6Н10О4
Акриловая С3Н402
Аспарагиновая C4H704N
Бензойная С7Н602
Борная Н2В03
127.
Примеры слабых электролитовСлабые кислоты:
Органические
(СН3СООН)
HF
H2 S
HCN
HnЭOm , m-n
2
Слабые основания:
NH4OH
Амины(C6H5NH3OH)
Me(OH)n , где Ме любой, кроме
щелочных и щелочноземельных
металлов
Для уксусной кислоты
Н
СН
СОО
;
СН 3 СООН
3
C (H ) C (CH 3COO )
5
0
KD
2 10 (25 C)
C (CH 3COOH)
128.
!!!Слабые
многоосновные кислоты и
многовалентные
основания диссоциируют
по ступеням.
Каждая следующая
ступень
слабее предыдущей
Fe(OH)2
1 ст. Fe(OH) 2
FeOH OH
К д1 1,2 10 2
2 ст. FeOH
Fe 2 OH
К д2 5,5 10 8
Kд2 << Kд1
H2S
1 ступень:
H 2S
H HS
С Н С HS
К д1
1,7 10 7
C H 2S
a1
K д1
С0
4 10 4
HS
H S2
2 ступень
СН СS
14
К д2
10
C HS
a2
K д2
a 1С 0
5 10 6
Kд << Kд
2
1
129.
Многоступенчатая диссоциация кислотыH 3 A H 2 A H
H 2 A HA2 H
H H A
K
2
H 3 A
I
H HA
K
H A
H A
K
HA
H A
K
K K K
2
2
2
2
3
HA A H
H 3 A A3 3 H
3
3
2
3
D
3
H 3 A
I
Константы ступенчатой диссоциации обычно
различаются на несколько порядков, причем
КI > K2 > K3
2
3
130.
Экспериментальная проверка теорииАррениуса показала, что для слабых
электролитов (уксусная кислота и т.п.),
теория справедлива, например, константа
КС (1) остается постоянной в достаточно
широком интервале концентраций.
Для сильных электролитов (минеральные
кислоты, соли и т.п.) КС изменяется с
концентрацией раствора.
131.
Для сильных электролитов даже в областинебольших концентраций константа
диссоциации сильно изменяется при
изменении концентрации.
Ниже в качестве примера приведены
значения констант диссоциации для
водных растворов КСl и СН3СООН при
298 К.
132.
Константы диссоциации для водныхрастворов КСl и СН3СООН при 298 К
СКС1 (моль/л)
КС (моль/л)
0,0001
0,0128
0,0010
0,0456
0,0100
0,1510
0.100
0,5349
CСН3СООН(моль/л)
KС 105(моль/л)
0,001
1,751
0,002
1,740
0,100
1,700
0,200
1,653
На эту слабость своей теории указывал ещё
сам С. Аррениус
133.
Воспоминанияоб активностях
134.
135.
Американский физик Дж. Льюис ввелпонятие активности как некоторой
формальной эффективной концентрации,
подстановка которой в термодинамические
уравнения для идеальных растворов делают
их справедливыми и для реальных
растворов.
В таком виде уравнения согласуются с
экспериментом. Для константы равновесия
диссоциации:
Ка
а H a A
a HA
136.
Экспериментально найденныеактивности (эффективные
концентрации) отличаются от
соответствующих аналитических
концентраций из-за взаимодействия
между ионами в растворах сильных
электролитов.
В растворах слабых электролитов
можно использовать концентрации,
а не активности.
137.
Активность связана сконцентрацией (с мольной долей)
через коэффициент активности:
ai = i xi
В случае моляльной концентрации mi:
ai = i mi
138.
Коэффициент активности компонентаявляется мерой отклонения свойств
раствора от свойств идеального раствора
той же концентрации:
ai
γi
xi
И чем сильнее активность отличается от
концентрации, тем сильнее коэффициент
активности отличается от единицы, тем
более неидеален раствор.
139.
В растворах электролитов, как правило,наблюдаются более значительные
отклонения от идеальности, чем в
растворах неэлектролитов.
Это объясняется наличием
электростатических межионных
взаимодействий, которые существенно
сильнее межмолекулярных (ван-дерваальсовских) взаимодействий.
140.
Существуют разные способы выражениякоэффициентов активности, которые
отвечают разным способам выражения
состава растворов
Концентрация
раствора
Единицы
измерения
Обозначения
Молярность
моль в 1 л
раствора
С
молярный
Моляльность
Молярная доля
С
моль в
1 кг
растворителя
m
m
практический
-
x
рациональный
141.
При введении активностей в уравнениедля константы электролитической
диссоциации получаем:
a a γ C γ C
Ka
a0
γ 0 C0
C C γ γ
γ γ
KC
C0
γ0
γ0
142.
Первый множительКС = С+·С-/Со
является функцией концентрации при её
изменении в широком интервале.
Величину КС называют кажущейся или
концентрационной константой
диссоциации.
143.
Ка называют термодинамической (истинной)константой диссоциации
Она не зависит от концентрации раствора.
В разбавленных растворах концентрационная
и термодинамическая константы практически
совпадают, так как i 1 и второй множитель
равен единице.
В общем случае Ка ≠ КД, поскольку ≠ 1 для
более или менее концентрированных
растворов.
144.
Константа диссоциации Ка зависит отприроды электролита, природы
растворителя и температуры.
Зависимость константы диссоциации от
температуры выражается уравнением
изобары Вант-Гоффа:
d ln K a D H
2
dT
RT
o
где DHo – тепловой эффект процесса
диссоциации (теплота диссоциации).
145.
Средние ионные величины146.
Нельзя приготовить раствор содержащийтолько катионы или анионы, т.е. нельзя
экспериментально определить
коэффициент активности для каждой из
этих заряженных частиц.
По этой причине вводится понятие о
среднем ионном коэффициенте
активности ионов, который
обозначается как и представляет собой
среднюю геометрическую величину от +
и отдельных ионов.
147.
Средний ионный коэффициент активности:γ γ γ
1/
Аналогично определяют и среднюю ионную
моляльность раствора т :
Активности ионов:
а γ m
а γ m
148.
Для вычисления средних ионных коэффициентовактивности выведено уравнение первого
приближения теории Дебая-Хюккеля,
называемое также предельным законом ДебаяХюккеля для среднего коэффициента
активности:
lg γ A | z z | I
при m < 0,01
где z+ и z_ заряды катиона и аниона, I ионная
сила раствора. Для отдельных ионов:
lg γ+ = −































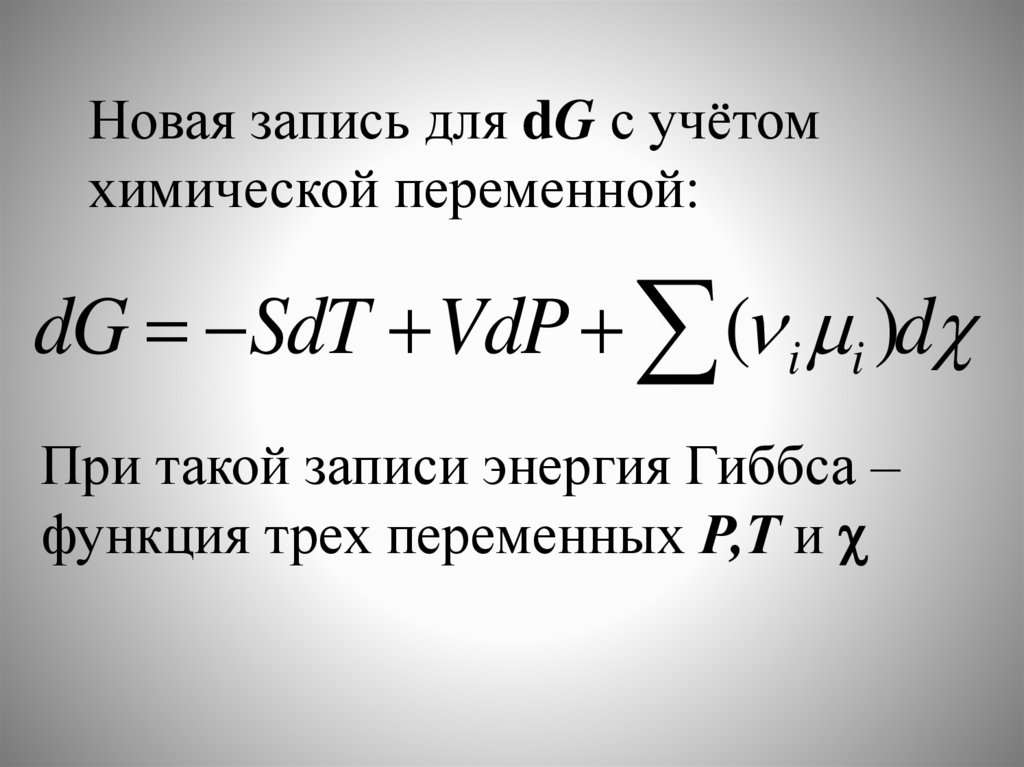

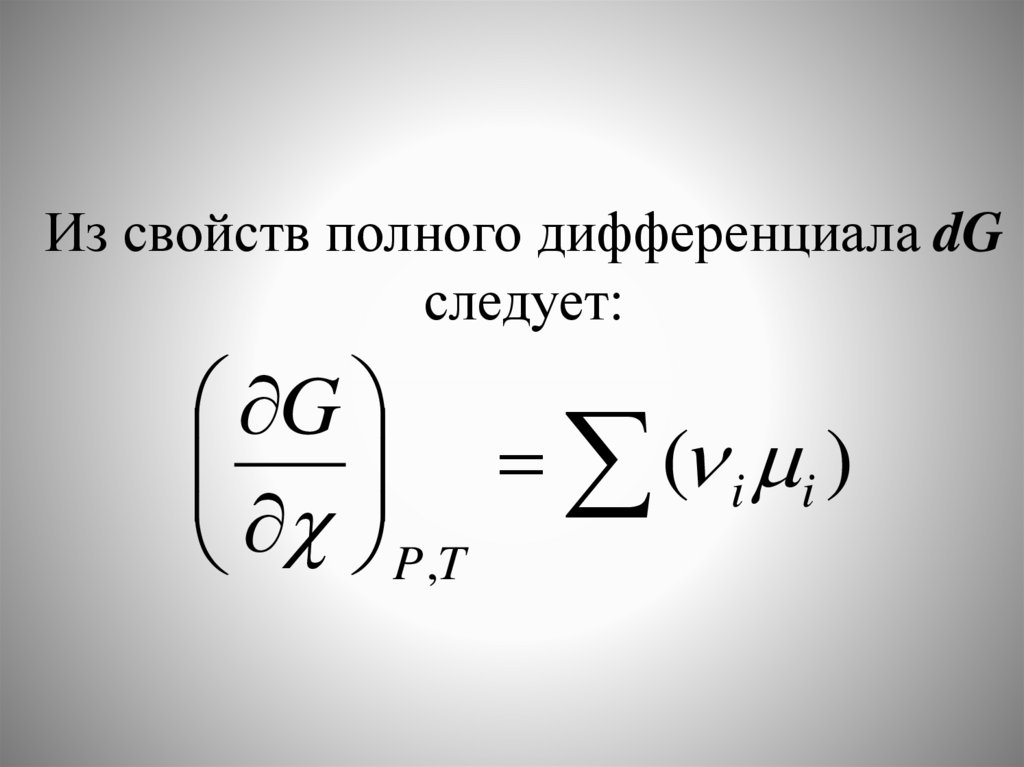
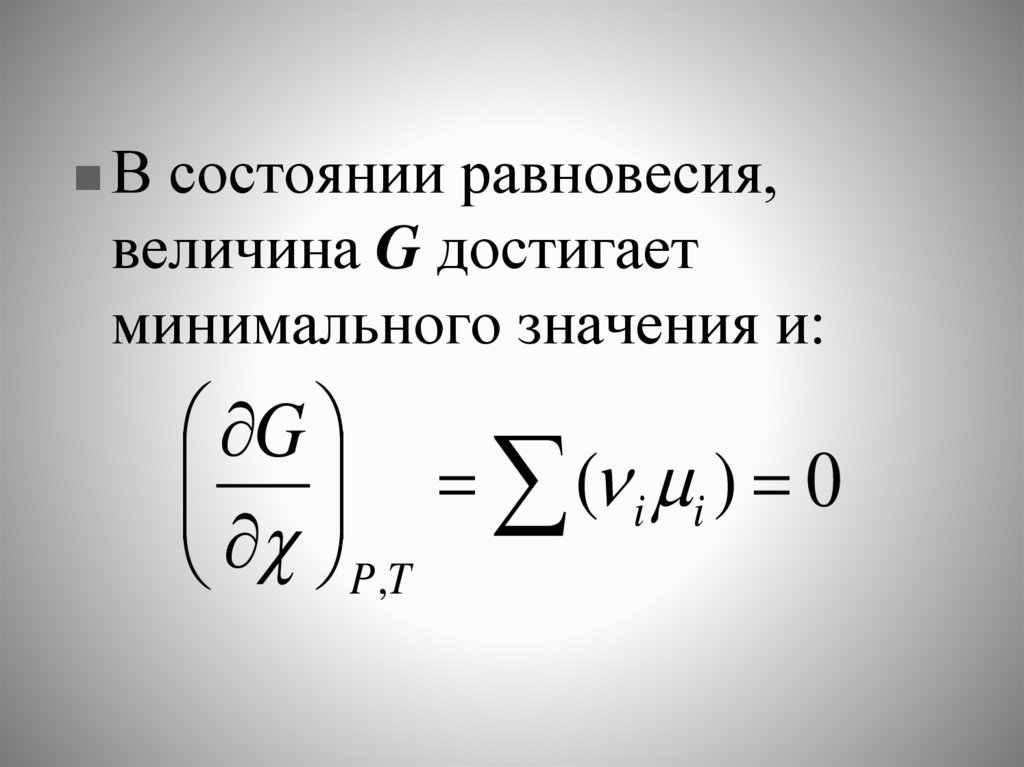









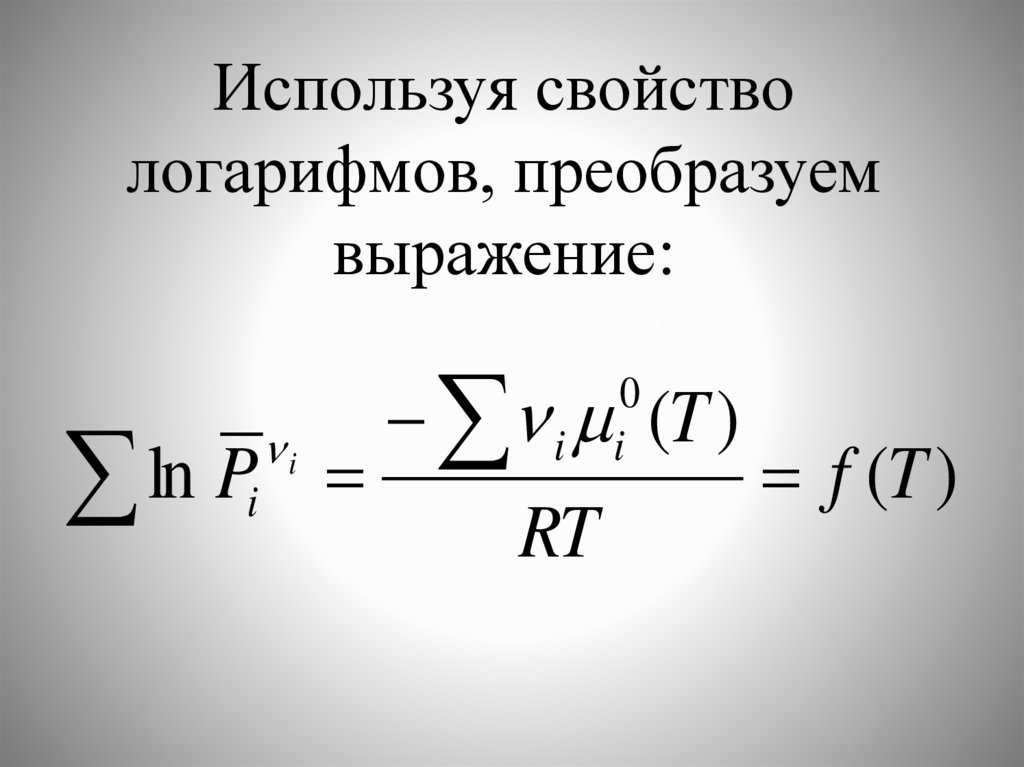












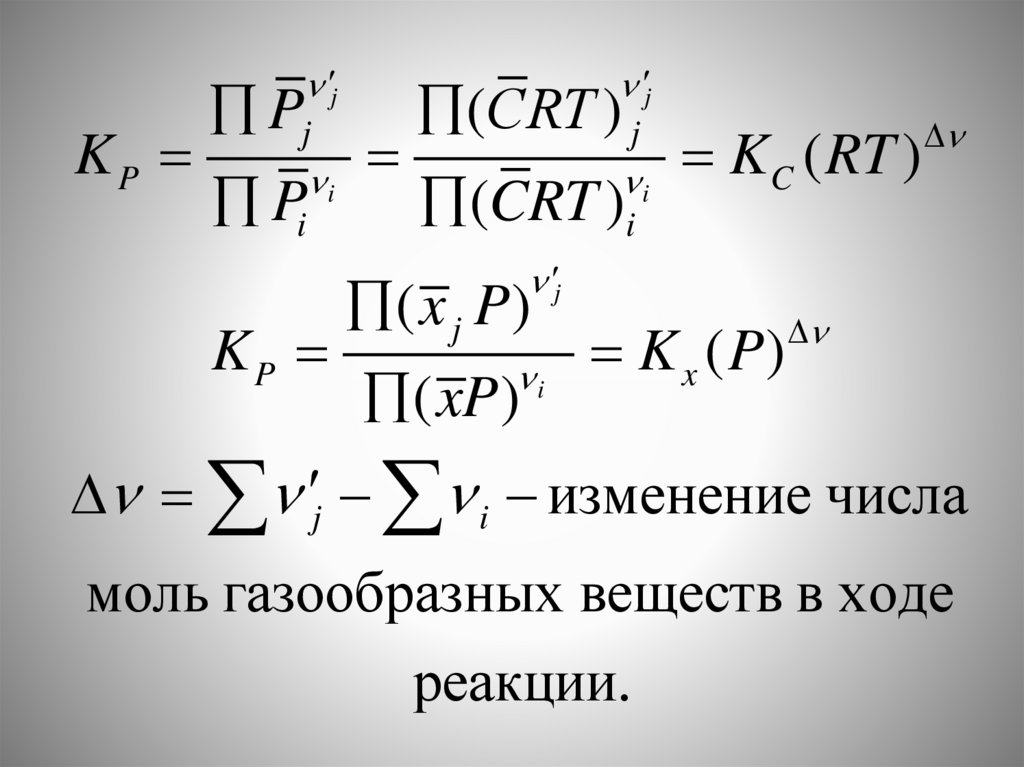











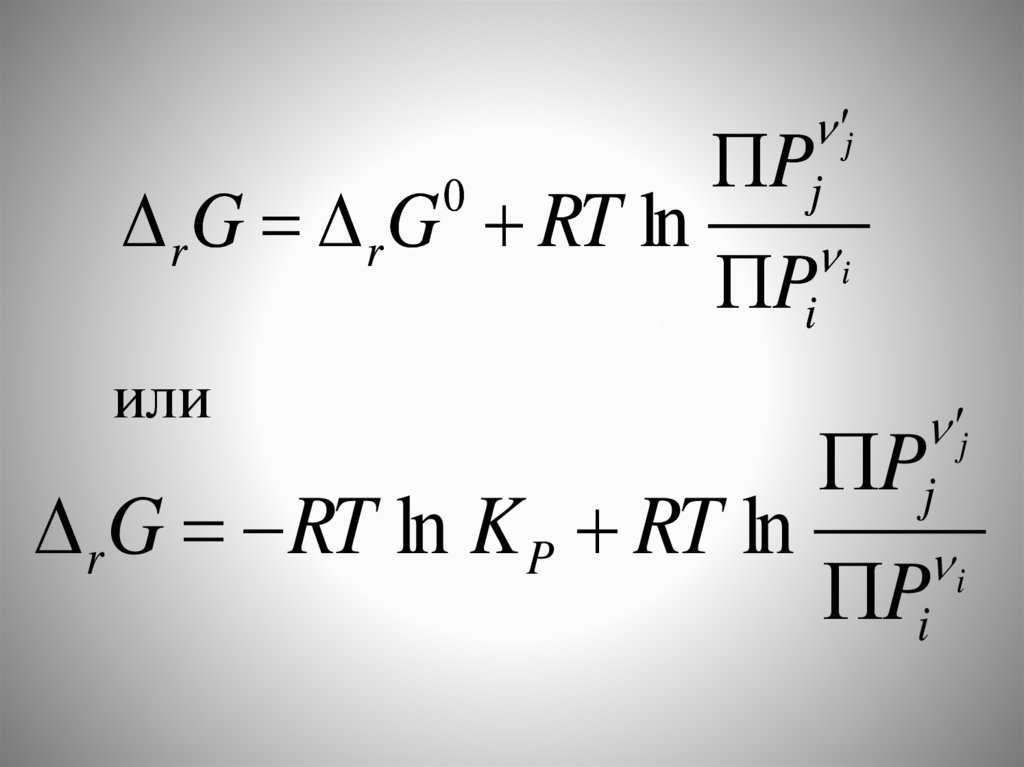









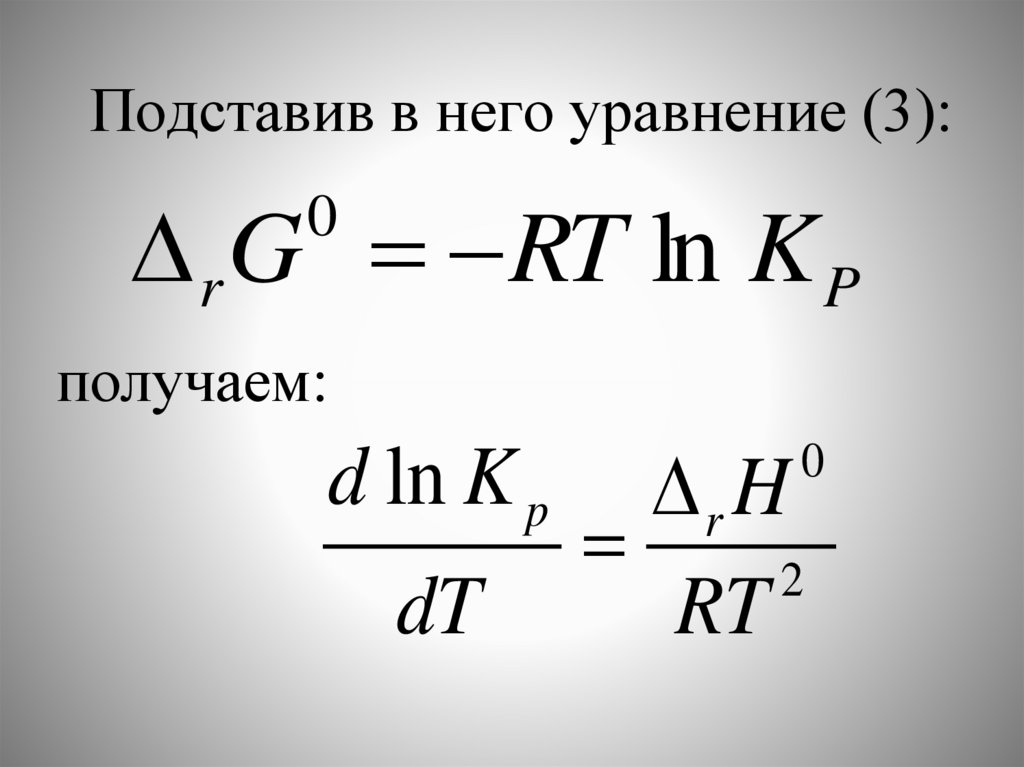













































































































































 chemistry
chemistry








