Экономико-математические методы анализа в управлении промышленным производством: методы динамического программирования

1. Экономико-математические методы анализа в управлении промышленным производством: методы динамического программирования

Выполнил ст.гр. МТП21-16-01
Л.З. Хисамова

2.

Динамическое программирование – это метод
оптимизации многошаговых и многоэтапных процессов,
критерий эффективности которых обладает аддитивным
свойством.
Динамическое моделирование – многошаговый
процесс, каждый шаг которого, соответствует поведению
экономической системы в определенный временный
период.
Сущность метода динамического
программирования сводится к составлению
функциональных уравнений, управляющих процессом, и
дальнейшему решению этих уравнений посредством
нестандартных вычислительных процедур.

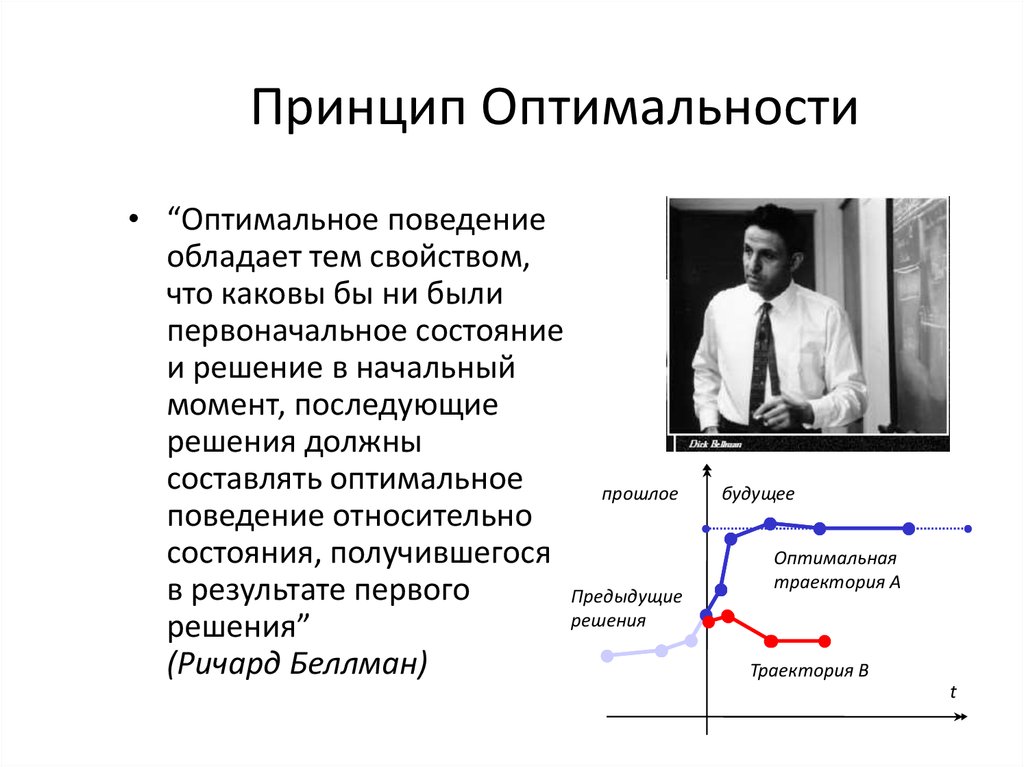
3. Принцип Оптимальности

• “Оптимальное поведение
обладает тем свойством,
что каковы бы ни были
первоначальное состояние
и решение в начальный
момент, последующие
решения должны
составлять оптимальное
прошлое
поведение относительно
состояния, получившегося
в результате первого
Предыдущие
решения
решения”
(Ричард Беллман)
будущее
Оптимальная
траектория A
Траектория B
t

4. Основное требование к задачам:

1)
2)
3)
4)
5)
Объектом исследования должна служить управляемая система
(объект) с заданными допустимыми состояниями и допустимыми
управлениями;
Задача должна позволять интерпретацию как многошаговый
процесс;
Задача не должна зависеть от количества шагов и быть
определенной на каждом из них;
Состояние системы на каждом шаге должно описываться
одинаковым набором параметров;
Последующее состояние, в котором оказывается система после
выбора решения на k-м шаге, зависит только от данного решения и
исходного состояния к началу k-го шага.

5. Алгоритм решения задач:

1. Выбирают способ деления процесса управления на шаги.
2. Определяют параметры состояния и переменные управления
на каждом шаге, записывают уравнения состояний.
3. Вводят целевые функции k-ого шага и суммарную целевую
функцию, а также условные оптимумы и условное
оптимальное управление на k-ом шаге .
4. Записывают в соответствии с обратной или прямой схемой
рекуррентные уравнения Беллмана и после выполнения
условной оптимизации получают две последовательности.
5. Определяют оптимальное значение целевой функции и
оптимальное решение .

6.

Спасибо за внимание!