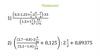Принцип Дирихле. Теоретический материал для решения задач с помощью принципа Дирихле

1.

Принцип Дирихле
Авторы: Бобина Анна Рындина Валерия. 5 класс, МАОУ «МГЛ при
МаГУ»
Научный руководитель: Елисеева И.В., преподаватель
математики

2.

Содержание
Введение
Глава 1. Принцип Дирихле
Кто такой Дирихле
Теоретический материал для решения задач с помощью принципа Дирихле
Интересные факты
Первая работа Дирихле
Глава 2. Практическая работа

3.

Введение.
Актуальность
На уроке «Решение нестандартных задач» нам учитель рассказал про
принцип Дирихле, нас этот принцип очень заинтересовал и нам захотелось
узнать побольше про этот принцип. После того как мы узнали про принцип
Дирихле мы провели опрос «Кто такой Дирихле?» среди опрошенных не было
ни одного человека кто ответил на этот вопрос. От сюда вытекает проблема
проекта: «Познакомить учащихся с великим математиком и показать принцип
решения задач». Данный материал не встречается в школьной программе, но
часто встречаются олимпиадные задачи для решения которых необходимо
использовать Принцип Дирихле.
Тема проекта: Принцип Дирихле

4.

Цель проекта.
Узнать и показать другим кто такой Дирихле, какие задачи можно
решить с помощью этого принципа и как нужно их решать.
Задачи проекта:
1.Исследовать литературу
2.Узнать кото такой Дирихле
3.Подобрать Теоретический материал для решения задач с помощью
принципа Дирихле
4.Подобрать и решить задачи
5.Узнать интересные факты
6.Узнать какие исследования делал Дирихле

5.

Глава 1

6.

Кто такой Дирихле
Иоганн Петер Густав Лежён Дирихле (13.02.1805 Дюрен –
5.05.1859 Гетенген), немецкий математик 1831-1855 гг.
профессор Берлинского, с 1855 г. Гетенгенского университетов.
Основал труды в области теории чисел и математического
анализа. Дирихле доказал теорему о существовании
бесконечно большого числа простых чисел во всякой
арифметической прогрессии из целых чисел первый член и
разность которой – числа взаимно простые.

7.

Даже прежде, чем он поступил в гимназию в Бонне в
1817 году, в возрасте 12 лет, он разработал страсть к
математике и провел свои карманные деньги на покупку
книг математике. В гимназии он был образцовым
учеником. В возрасте от 16 Дирихле завершил свою
квалификацию школу и был готов поступить в
университет. Тем не менее, стандарты в немецких
университетах не были высокими, в это время так
Дирихле решил и учиться в Париж. Интересно отметить,
что несколько лет спустя стандартов в немецких
университетах стали бы лучшими в мире, а сам Дирихле
будет играть рукой в преобразовании.
Дирихле отправился во Францию проведения с ним
Гаусса "с Арифметических работы он храниться и
постоянно держали с ним, как другие могут делать с
Библией.

8.

В 1827г. устраивается на должность
приват-доцента университета Бреслау
(Вроцлав).
В 1829 г. он перебирается в Берлин,
где проработал непрерывно 26 лет,
сначала как доцент. Затем с 1831 г. как
экстраординарный профессор.
С 1839 г. как ординарный профессор
Берлинского университета.
В 1855 г. Дирихле становится в
качестве преемника Гаусса
профессором высшей математики в
Гёттингенском университете.
Биография

9.

Среди учеников Дирихле были:
* Леопольд Кронекер
* Рудольф Липшиц
* Фердинанд Эйзенштейн

10.

Теоретический материал для решения задач с помощью
принципа Дирихле
У математиков встречаются весьма странные "принципы", которыми они никогда не
поступаются. Впрочем, любой здравомыслящий человек, ознакомившись с этими
принципами, вынужден их признать. Вот, например, так называемый принцип Дирихле.
Математики очень любят объяснение этого принципа сводить, к примеру кроликов в
клетках. Поступим так же и мы.
Если в ста (или n) клетках сидит не менее 101 (или n+1) кроликов, то хотя бы в одной клетке
находится более одного кролика. Удивительно, что на основе такого простого и даже чуть
наивного принципа математикам удается решать весьма трудные задачи, доказывать
красивые теоремы, причем не только элементарные.

11.

Чтобы правильно решить задачу на Дирихле нужно найти, где зайцы, а где
клетки
Например: На складе имеется по 200 сапог 41, 42 и 43 размеров, причем среди этих
600 сапог 300 левых и 300 правых. Докажите, что из них можно составить не менее
100 годных пар обуви

12.

13.

Интересные факты
Самая популярная в русскоязычной математической литературе
формулировка принципа Дирихле следующая:"Нельзя рассадить трёх
зайцев по двум клеткам так, чтобы в каждой клетке сидели по одному
зайцу".
Поэтому в русскоязычной математической литературе принцип Дирихле
называется принципом зайцев или кроликов. В англоязычной литературе
принцип называется похожим образом: Pigeonhole Principle (принципом
голубиной норки).
Принцип Дирихле представляет собой настолько очевидное утверждение,
что на первый взгляд даже непонятно, почему он является весьма
эффективным методом решения задач, дающим во многих случаях

14.

15.

Глава 2.
Практическая часть

16.

Задачи

17.

1.В классе 30 человек
Саша Иванов сделал в диктанте 13 ошибок, а
остальные меньше. Докажите что по крайней мере 3 ученика сделали ошибки
поровну.

18.

Решение
Здесь “зайцы” – ученики, “клетки” – число сделанных ошибок. В клетку 0 “посадим” всех, кто
сделал ни одной ошибки, в клетку 1 – тех, у кого одна ошибка, в клетку 2 – две … и так до клетки
13, куда попал один Саша Иванов.Теперь применим принцип Дирихле. Докажем утверждение
задачи от противного. Предположим, никакие три ученика не сделали по одинаковому числу
ошибок, то есть в каждую из “клеток”: 0, 1, 2, …, 12 попало меньше 3школьников. Тогда в каждой
из них два человека или меньше, а всего в этих 13 клетках не более 2×13=26 человек. Добавив
Сашу Иванова, все ровно не наберем 30 ребят. Противоречие. Значит, наше предположение
неверно и, по крайней мере, трое учеников сделали поровну ошибок.

19.

2.В самолете летят 380 пассажиров.
Докажите что по крайней мере двое из
них родились в один и тот же день года.

20.

Решение
Всего в году 365 или 366 дней, а пассажиров в самолете 380 – значит, их дни рождения
не могут приходиться на различные дни. Вообще если пассажиров больше, чем 366, то
хотя бы у двоих дни рождения совпадают. А вот если пассажиров 366 не исключено, что
все они родились в разные дни года, но это маловероятно (согласно теории вероятностей в
случайно выбранной группе численностью свыше 22 человек совпадение дней рождения у
некоторых из них более вероятно, нежели то, что у всех дни рождения приходятся на
разные дни года)

21.

Задача 3. На Земле больше шести миллиардов жителей, людей старше 150
лет не существует. Докажите, что на Земле есть два человека, родившихся
одновременно с точностью до секунды.

22.

Решение
Здесь зайцы-люди, а клетки-время рождения. Что бы найти время рождения нужно
найти: год(365), месяц(30), день(24), час(60), минута(60), секунда и наконец сколько лет
максимум проживает человек(150). Ну а зайцев мы знаем сколько-6000000000человек.
6000000000:(365*30*24*60*60*150)= 6000000000: (10950*24*60 *60*150)=
6000000000:(262800*60 *60*150)= 6000000000:(946080000*150)=
6000000000:141912000000=-это меньше 2х, а значит нет таких людей

23.

Задача 4. Математический кружок посещают 15
учеников. Докажите, что найдутся как минимум 2
ученика, отмечающих дни рождения в один
месяц.

24.

Решение:
Пусть 15 учеников будут «зайцы». Тогда «клетками» будут месяцы
года, их 12. Так как 15 больше 12, то, по принципу Дирихле, найдется,
как минимум, одна клетка, в которой будут сидеть, по крайней мере, 2
«зайца». То есть, найдется месяц, в котором будут отмечать дни
рождения не менее 2учеников класса.А это и требовалось доказать.

25.

Задача 5.В магазин привезли 34 ящика с яблоками трех
сортов, причем в каждом ящике лежали яблоки какого-то
одного сорта. Можно ли найти 12 ящиков с яблоками одного
сорта?

26.

Имеем 3 «клетки» (сорта), 34=3×11+1. В каждую
«клетку» (сорт) мы можем «посадить» 11 «зайцев»
(ящиков) и еще у нас есть один ящик. Значит, в какуюто «клетку» (сорт) мы посадим еще одного «зайца»
(ящик). Таким образом, можно утверждать, что, по
крайней мере, в 12 ящиках находятся яблоки одного

27.

Задача 6.В классе 35 учеников. Можно ли
утверждать, что среди них найдутся хотя бы 2 ученика,
фамилии которых начинаются с одной
буквы?

28.

Решение:
Обозначим 35 учеников за «зайцев», за буквы за «клетки». В русском алфавите 33
буквы. Фамилии не могут начинаться на Ы, Ъ и Ь. Так как 35 больше 30, то, по принципу
Дирихле, найдется 2 ученика, у которых фамилии начинаются с одной буквы.

29.

7. В городе живет 200 тысяч жителей. Докажите, что
в городе найдутся хотя бы 2 человека с одинаковым
числом волос на голове. Считайте, что у человека на
голове не больше 150 тысяч волос.Задача

30.

Решение:
Примем жителей за «зайцев», их 200 тысяч. А клеток лишь
150 тысяч с номерами от 0 до 150 тысяч. Так как «зайцев» жителей гораздо больше, чем «клеток», то, по крайней мере, в
одной «клетке» окажется 2 «зайца», то есть в городе найдутся
2 человека с одинаковым числом волос на голове.

31.

Глава 3.
Заключение

32.

Мы узнали кто такой Дирихле, Дирихле - это немецкийматематик, профессор
Берлинского и Гетенгенского университетов. Познакомились с принципом Дирихле: нельзя
посадить трех зайцев в две клетки так, что бы каждой клетки было одинаковое количество
зайцев и узнали как нужно их решать. Узнали несколько фактов и первую работу Дирихле.
Прорешали несколько задач на этот принцип

33.

Литературные справочники
Центр научно-технологического творчества учащейся молодежи
(http://tsnttum.narod.ru/kruzhki/mathematics/)
My shared (http://www.myshared.ru/slide/54081/)
http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Dirichlet.html