Similar presentations:
Метод швидкого сортування (QuickSort)
1.
Методшвидкого
сортування
(QuickSort)
2.
Швидке сортування (англ. QuickSort) — алгоритм сортування, добре
відомий, як алгоритм розроблений
Чарльзом Хоаром, який не потребує
додаткової пам'яті і виконує у
середньому O(n log n) операцій.
Однак, у найгіршому випадку робить
O(n2) порівнянь. Оскільки алгоритм
використовує дуже прості цикли і
операції, він працює швидше інших
алгоритмів, що мають таку ж
асимптотичну
оцінку
складності.
Наприклад, зазвичай більш ніж удвічі
швидший порівняно з сортуванням
злиттям.
3.
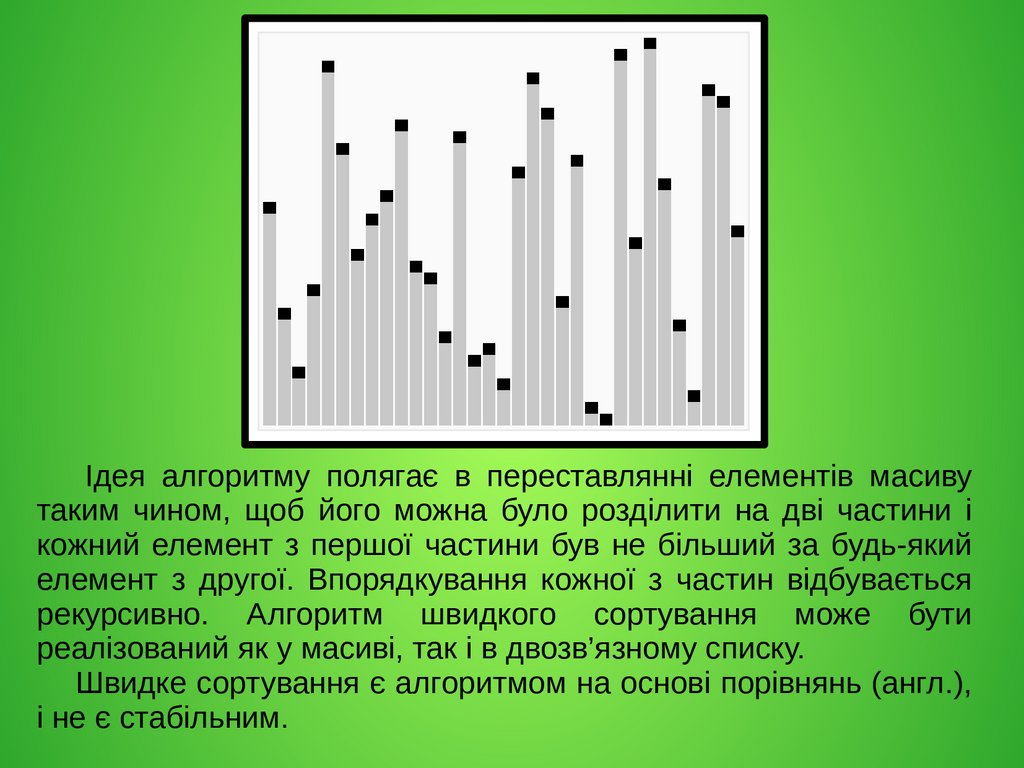
Ідея алгоритму полягає в переставлянні елементів масивутаким чином, щоб його можна було розділити на дві частини і
кожний елемент з першої частини був не більший за будь-який
елемент з другої. Впорядкування кожної з частин відбувається
рекурсивно. Алгоритм швидкого сортування може бути
реалізований як у масиві, так і в двозв’язному списку.
Швидке сортування є алгоритмом на основі порівнянь (англ.),
і не є стабільним.
4.
Алгоритм швидкого сортування було розроблено ЧарльзомХоаром (C. A. R. Hoare) у 1962 під час роботи у маленькій
британській компанії Elliott Brothers.
5.
Загальна схема медотушвидкого сортування така:
З масиву вибирається деякий опорний елемент a;
Запускається процедура поділу масиву, що переміщає всі
ключі, менші, або рівні a, вліво від нього, а всі ключі, більші,
або рівні a – вправо;
Тепер масив складається з двох підмножин, причому ліва
менше, або дорівнює правій;
Для обох підмасивів: якщо в підмасиві більш двох елементів,
рекурсивно запускаємо ту ж процедуру
Наприкінці вийде цілком відсортована послідовність.
6.
QuickSort є істотно поліпшеним варіантом алгоритмусортування за допомогою прямого обміну (його варіанти
відомі як " Бульбашкова сортування "і" Шейкерная
сортування "), відомого, в тому числі, своєю низькою
ефективністю.
Принципова відмінність полягає в тому, що після кожного
проходу елементи діляться на дві незалежні групи.
Цікавий факт: поліпшення самого неефективного прямого
методу сортування дало в результаті ефективний
покращений метод.
Сортування бульбашкою
7.
8.
Оцінка ефективностіКращий випадок
Середнє
Для цього алгоритму
найкращий випадок якщо в кожній ітерації
кожен
з
подмассіва
ділився б на два рівних
по величині масиву. В
результаті
кількість
порівнянь,
зроблених
швидкої
сортуванням,
було
б
дорівнює
значенню рекурсивного
виразу C N = 2C N / 2 + N,
що в явному виразі дає
приблизно
N
lg
N
порівнянь. Це дало б
найменший
час
сортування
Дає в середньому O (n log n)
обмінів при упорядкуванні n
елементів. У реальності саме
така ситуація зазвичай має
місце при випадковому порядку
елементів і виборі опорного
елемента з середини масиву
або випадково.
На практиці швидке сортування
значно
швидше,
ніж
інші
алгоритми з оцінкою O (n lg n),
по причині того, що внутрішній
цикл алгоритму може бути
ефективно реалізований майже
на будь архітектурі. 2C N / 2
покриває витрати по сортуванню
двох отриманих подмассіва; N це вартість обробки кожного
елемента, використовуючи один
або інший покажчик.
Найгірший
випадок
Гіршим
випадком,
очевидно, буде такий,
при якому на кожному
етапі
масив
буде
розділятися
на
вироджений подмассів
з
одного
опорного
елемента
і
на
подмассів з усіх інших
елементів. Таке може
статися, якщо в якості
опорного на кожному
етапі буде обраний
елемент
або
найменший,
або
найбільший
з
усіх
оброблюваних.
9.
ПоліпшенняПри виборі опорного елемента з даного діапазону випадковим чином гірший
випадок стає дуже малоймовірним і очікуваний час виконання алгоритму сортування
- O (n lg n).
Вибирати опорним елементом середній з трьох (першого, середнього і останнього
елементів). Такий вибір також спрямований проти гіршого випадку.
Щоб уникнути досягнення небезпечної глибини рекурсії в гіршому випадку (або при
наближенні до нього) можлива модифікація алгоритму, що усуває одну гілку рекурсії:
замість того, щоб після поділу масиву викликати рекурсивно процедуру поділу для
обох знайдених подмассіва, рекурсивний виклик робиться тільки для меншого
подмассіва, а більший обробляється в циклі в межах цього ж виклику процедури. З
точки зору ефективності в середньому разі різниці практично немає: накладні
витрати на додатковий рекурсивний виклик і на організацію порівняння довжин
подмассіва і циклу - приблизно одного порядку. Зате глибина рекурсії ні за яких
обставин не перевищить log 2 n, а в гіршому випадку виродженого поділу вона
взагалі буде не більше 2 - вся обробка пройде в циклі першого рівня рекурсії.
Розбивати масив не на дві, а на три частини (див. Dual Pivot Quicksort).
10.
Переваги і недолікиПереваги:
Один з самих швидкодіючих (на практиці)
з алгоритмів внутрішнього сортування
загального призначення.
Простий в реалізації.
Вимагає лише O(lg n) додаткової
пам'яті для своєї роботи. (Не покращений
рекурсивний алгоритм в гіршому випадку
пам'яті)
Добре
поєднується
з
механізмами
кешування і віртуальної пам'яті.
Існує ефективна модифікація (алгоритм
Седжвіка) для сортування рядків спочатку
порівняння
з
опорним
елементом тільки по нульовому символу
рядка, далі застосування аналогічної
сортування для "більшого" і "меншого"
масивів теж по нульовому символу, і для
"рівного" масиву по вже першого символу.
Працює на пов'язаних списках та інших
структурах з послідовним доступом.
Недоліки:
Сильно деградує по швидкості
При невдалих виборах опорних
елементів, що може трапитися при
невдалих вхідних даних. Цього можна
уникнути,
використовуючи
такі
модифікації алгоритму, як Introsort,
або ймовірносно, вибираючи опорний
елемент випадково, а не фіксованим
чином.
Наївна реалізація алгоритму може
привести до помилки переповнення
стека, так як їй може знадобитися
зробити
O (n)
вкладених
рекурсивних викликів. У покращених
реалізаціях, в яких рекурсивний
виклик
відбувається тільки
для
сортування меншою з двох частин
масиву, глибина рекурсії гарантовано
не перевищить O(lg n) .
Нестійкий - якщо потрібна стійкість,
доводиться розширювати ключ.









 informatics
informatics








