Законы распределения непрерывных случайных величин, используемые в теории надежности

1.

Л6-1
ЛЕКЦИЯ 6
Законы распределения
непрерывных случайных
величин, используемые
в теории надежности

2.

Л6-2
описания непрерывных
II Законы для
случайных величин
3
Распределение непрерывных случайных
величин Вейбулла-Гнеденко
Применяется для невосстанавливаемых систем на
начальном этапе эксплуатации в интервале [0,t]. Вероятность
безотказной работы приведена на рис. 3.1:
P (t ) e
tb
a
(t≥0, a>0, b>0)
a – параметр масштаба,
b – параметр формы
P(t)
b>1
b<1
0
Рис. 3.1
t

3.

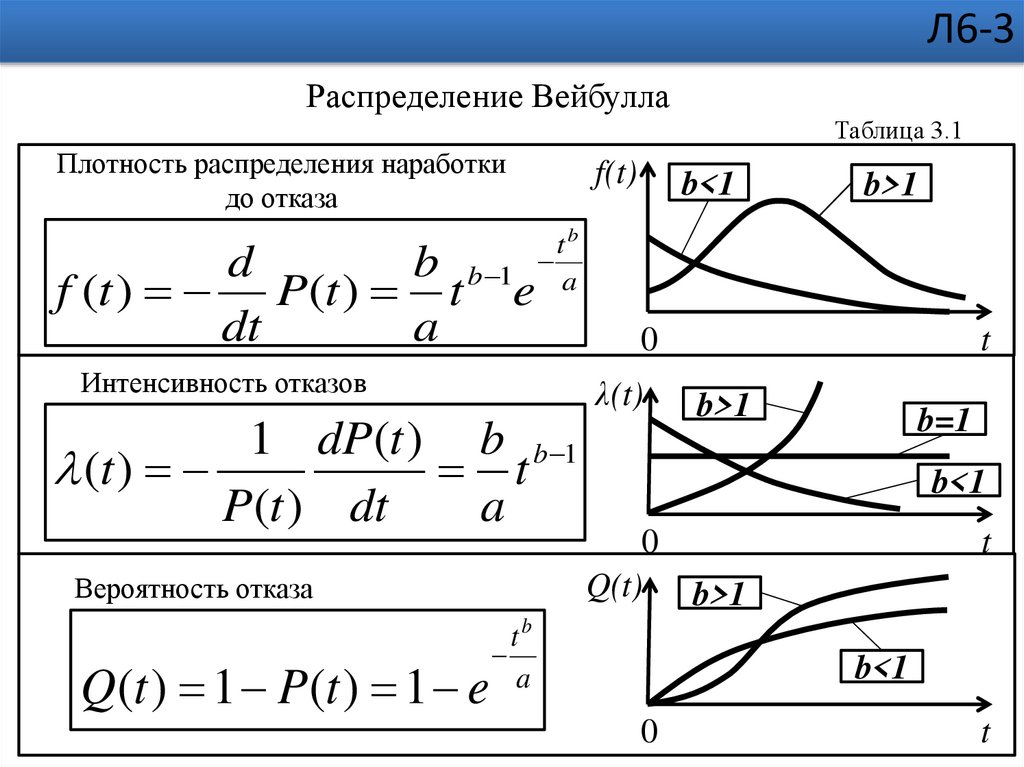
Л6-3
Распределение Вейбулла
Таблица 3.1
Плотность распределения наработки
до отказа
d
b
f (t ) P(t ) t
dt
a
f(t)
b<1
b>1
tb
b 1
a
e
0
Интенсивность отказов
λ(t)
1 dP(t ) b b 1
(t )
t
P(t ) dt
a
Вероятность отказа
Q(t ) 1 P (t ) 1 e
t
b>1
b=1
b<1
0
Q(t) b>1
tb
a
t
b<1
0
t

4.

Л6-4
4
Экспоненциальное распределение
Особенности:
● это частный случай распределения Вейбулла и реализуется при b=1;
● показатели безотказности на данный момент времени не зависят от
предыстории эксплуатации системы (если до этого момента времени
отказов не происходило);
● постоянство интенсивности отказов (λ=const);
● так как средняя наработка до отказа
t
1
T0
, то P(t ) e T e 1 0,368;
0
● характерно для большинства сложных систем, содержащих большое
количество невосстанавливаемых элементов, имеющих
преимущественно внезапные отказы (вследствие наличия скрытых
дефектов);
● применяется для восстанавливаемых систем с простейшим потоком
отказов.

5.

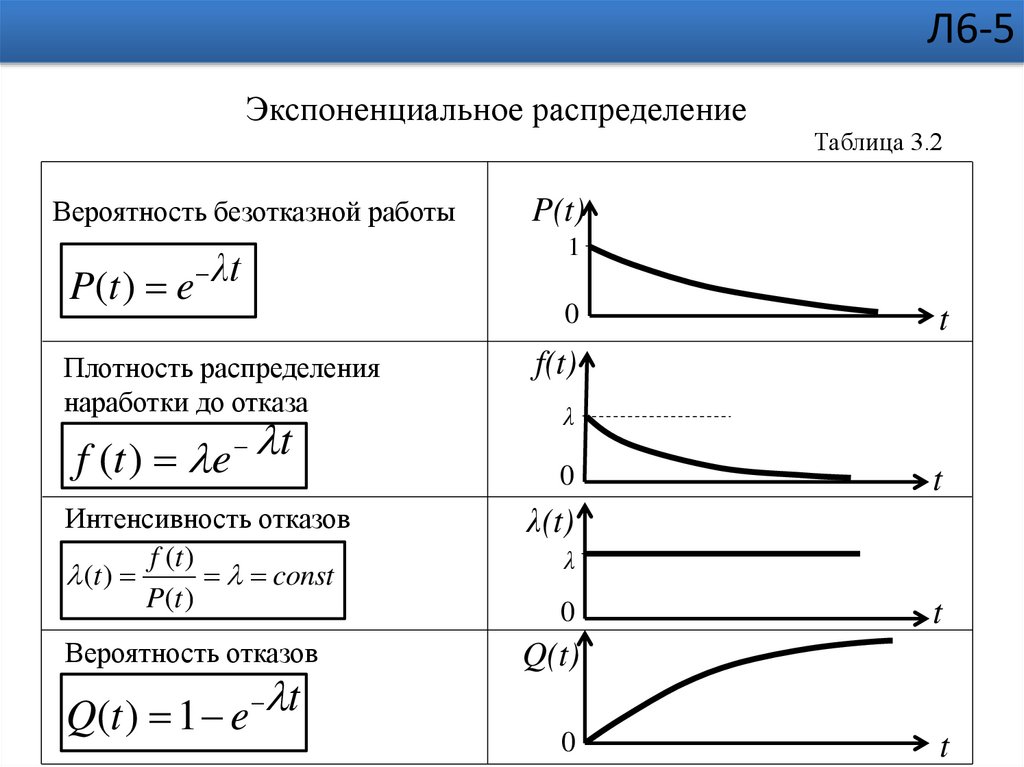
Л6-5
Экспоненциальное распределение
Вероятность безотказной работы
Таблица 3.2
P(t)
1
P(t ) e λt
0
Плотность распределения
наработки до отказа
t
f (t ) e
f(t)
λ
0
Интенсивность отказов
f (t )
(t )
const
P(t )
λ(t)
Вероятность отказов
Q(t)
t
Q(t ) 1 e
t
t
λ
0
t
0
t

6.

Л6-6
5
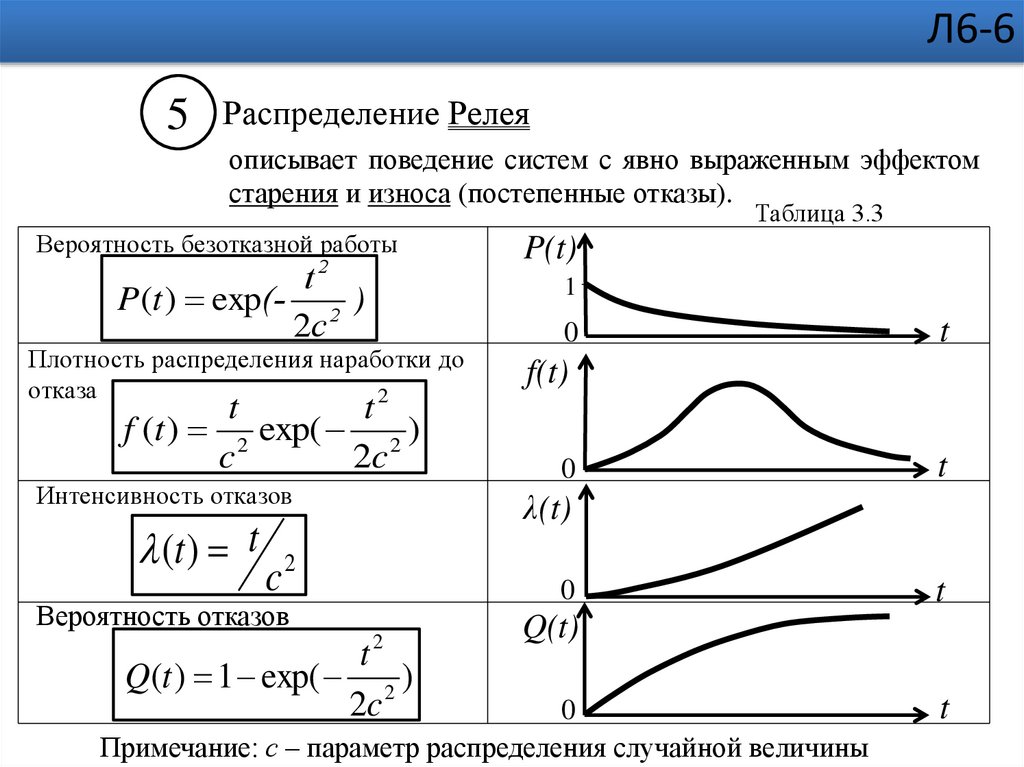
Распределение Релея
описывает поведение систем с явно выраженным эффектом
старения и износа (постепенные отказы).
Таблица 3.3
Вероятность безотказной работы
2
t
P(t ) exp(- 2 )
2c
P(t)
1
Плотность распределения наработки до
отказа
2
t
t
f (t ) 2 exp( 2 )
c
2c
Интенсивность отказов
0
t
f(t)
0
t
λ(t)
(t ) t 2
c
0
Вероятность отказов
2
t
Q(t ) 1 exp( 2 )
2c
t
Q(t)
0
Примечание: с – параметр распределения случайной величины
t

7.

Л6-7
6
Нормальный закон распределения (закон Гаусса).
Особенности:
● закон Гаусса называют предельным, т.к. к нему
приближаются другие законы распределения непрерывных
случайных
величин.
Например,
биноминальное
распределение при достаточно больших значениях МОЖ
исследуемой случайной величины очень близко к
нормальному;
● случайная величина может принимать любые значения от
- ∞ до + ∞, но возможные значения случайной наработки до
отказа могут быть только положительными. Поэтому
наработку рассматривают в усеченном интервале времени (0,
+ ∞), т.е. используется усеченное нормальное распределение.

8.

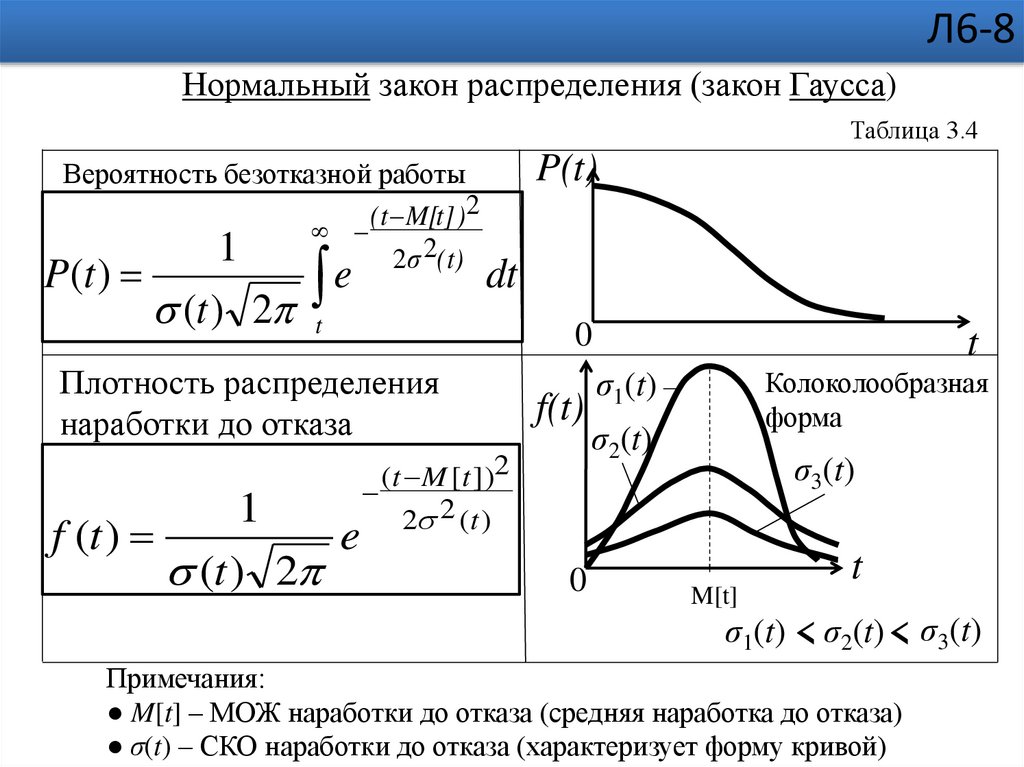
Л6-8
Нормальный закон распределения (закон Гаусса)
Таблица 3.4
Вероятность безотказной работы
2
(t
M[t])
1
2σ 2(t)
P(t )
e
(t ) 2
P(t)
dt
t
0
Плотность распределения
наработки до отказа
1
f (t )
e
(t ) 2
f(t)
(t M [t ])2
2 2 (t )
0
t
σ1(t)
Колоколообразная
форма
σ2(t)
σ3(t)
M[t]
t
σ1(t) < σ2(t) < σ3(t)
Примечания:
● M[t] – МОЖ наработки до отказа (средняя наработка до отказа)
● σ(t) – СКО наработки до отказа (характеризует форму кривой)

9.

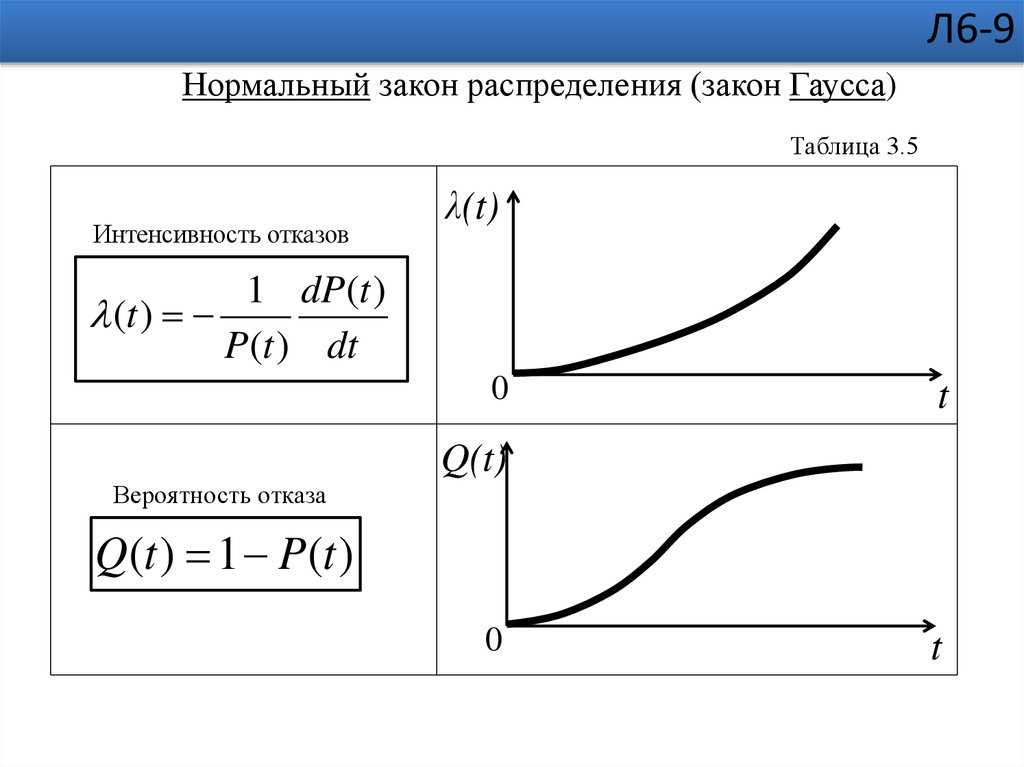
Л6-9
Нормальный закон распределения (закон Гаусса)
Таблица 3.5
Интенсивность отказов
λ(t)
1 dP(t )
(t )
P(t ) dt
0
t
Q(t)
Вероятность отказа
Q (t ) 1 P (t )
0
t

10.

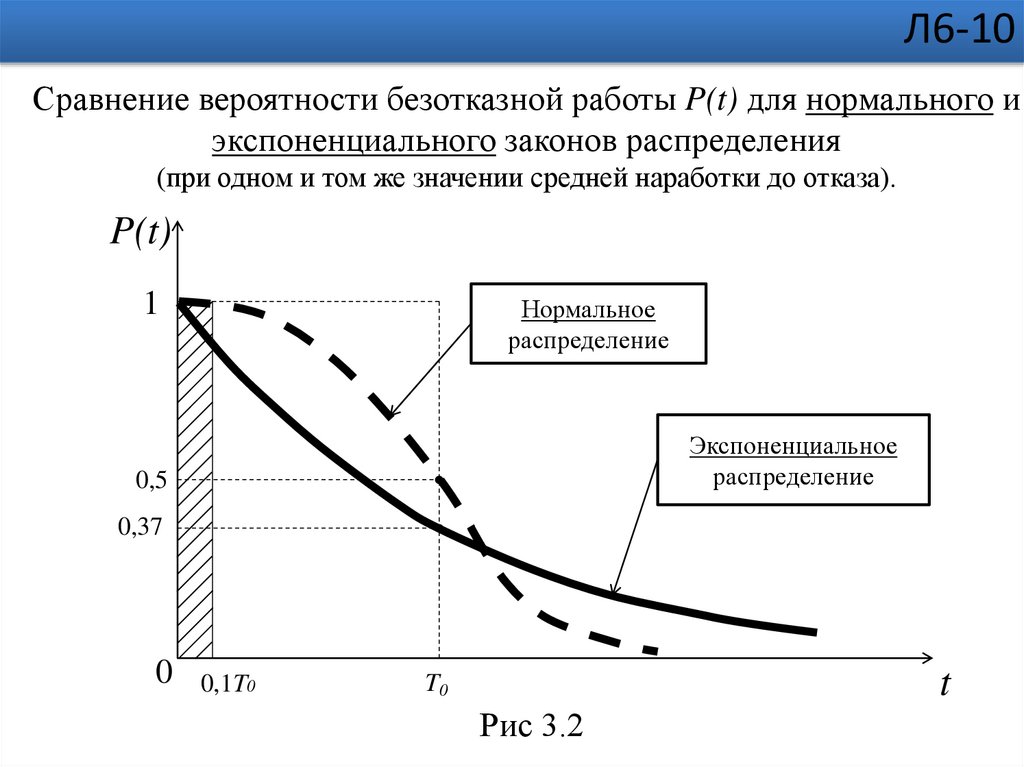
Л6-10
Сравнение вероятности безотказной работы P(t) для нормального и
экспоненциального законов распределения
(при одном и том же значении средней наработки до отказа).
P(t)
1
Нормальное
распределение
Экспоненциальное
распределение
0,5
0,37
0
0,1T0
t
T0
Рис 3.2

11.

Л6-11
Выводы из сравнения P(t) для нормального и
экспоненциального законов распределения случайной
величины:
● системы, время безотказной работы которых
подчинены нормальному закону распределения в интервале (0,
T0) имеют более высокие показатели надежности, чем системы
с экспоненциальным законом распределения;

12.

Л6-12
● заштрихованный участок от 0 до 0,1Т0 – это
промежуток времени, охватывающий 90%-ный гамма-ресурс
(при 99,9% этот участок сокращается до 0,001Т0). При этом
различие между нормальным и экспоненциальным законах
незначительно, поэтому при P(t)=0,95 и выше используется
экспоненциальный закон (как наиболее простой).

13.

Л6-13
На
этой
основе
разработаны
действующие
госстандарты, регламентирующие требования к надежности
систем. В них, в частности, принята постоянной
интенсивность отказов (λ(t)=λ=const) в течение наработки,
что соответствует экспоненциальному закону распределения

14.

Л6-14
7
Гамма-распределение или гамма-процентное
распределение
Гамма-распределение или гамма-процентное
распределение (например, гамма-процентный ресурс или
гамма-процентный срок службы) – это наработка (или
календарная продолжительность эксплуатации изделия) в
течение которой изделие достигает (или не достигает)
предельного состояния с заданной вероятностью γ,
выраженной в процентах.
Это распределение используется для описания:
а) наработки изделия с резервированием;
б) времени восстановления;
в) распределения постепенных отказов изделия вследствие
износа.

15.

Л6-15

16.

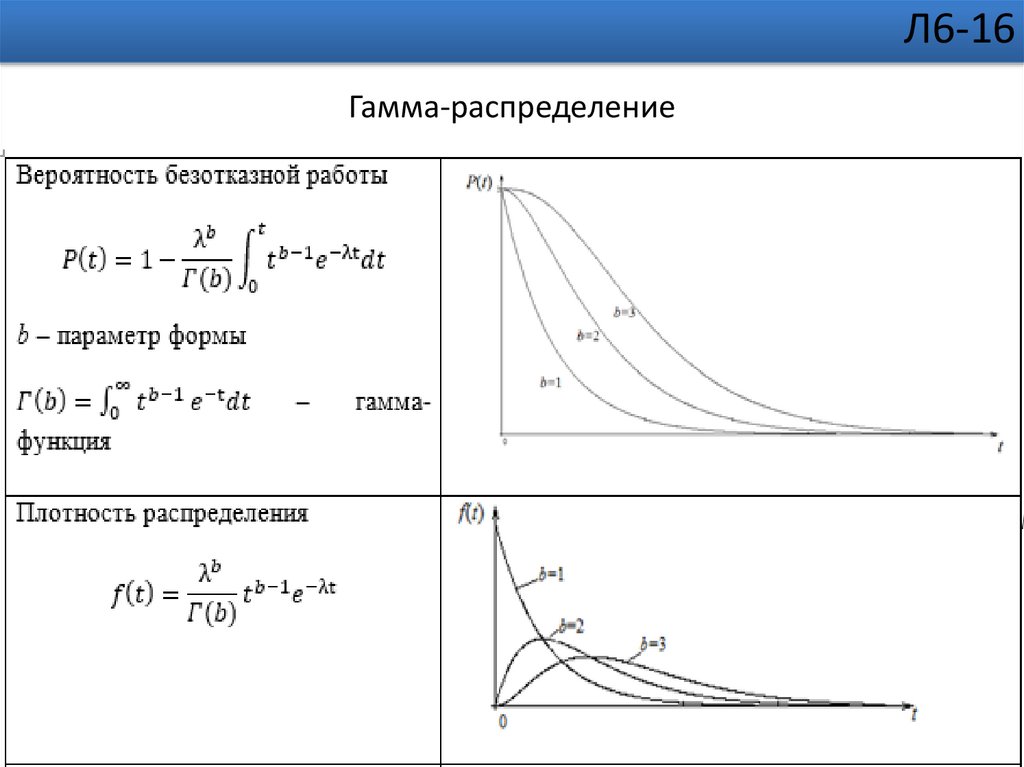
Л6-16
Гамма-распределение

17.

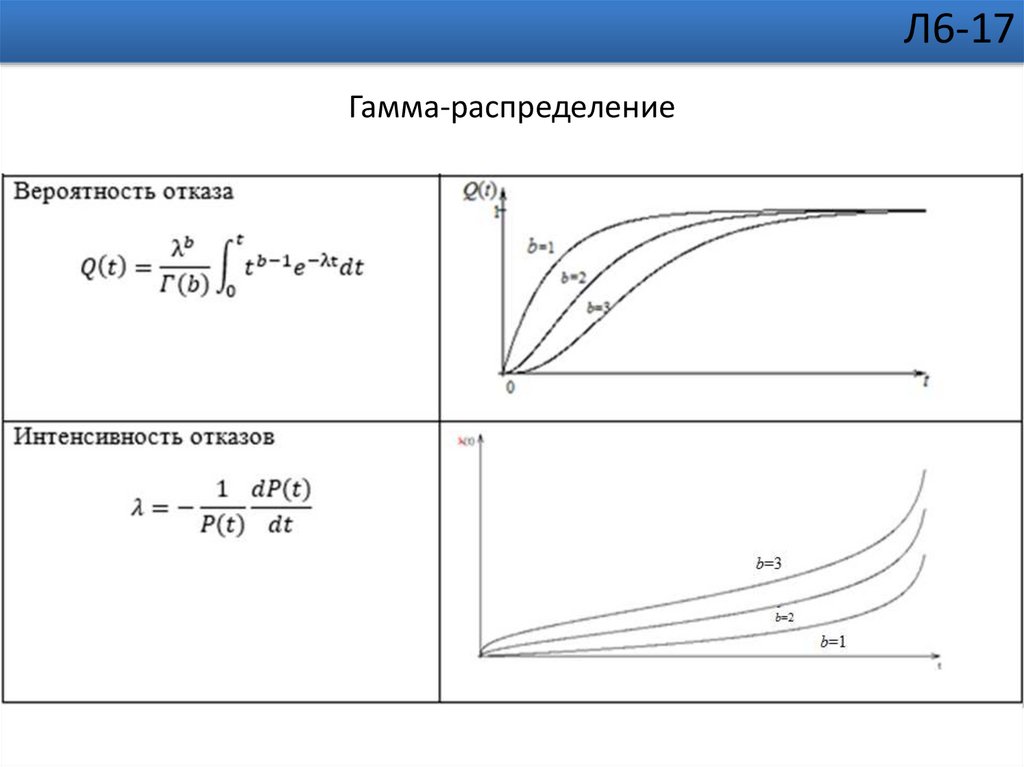
Л6-17
Гамма-распределение

18.

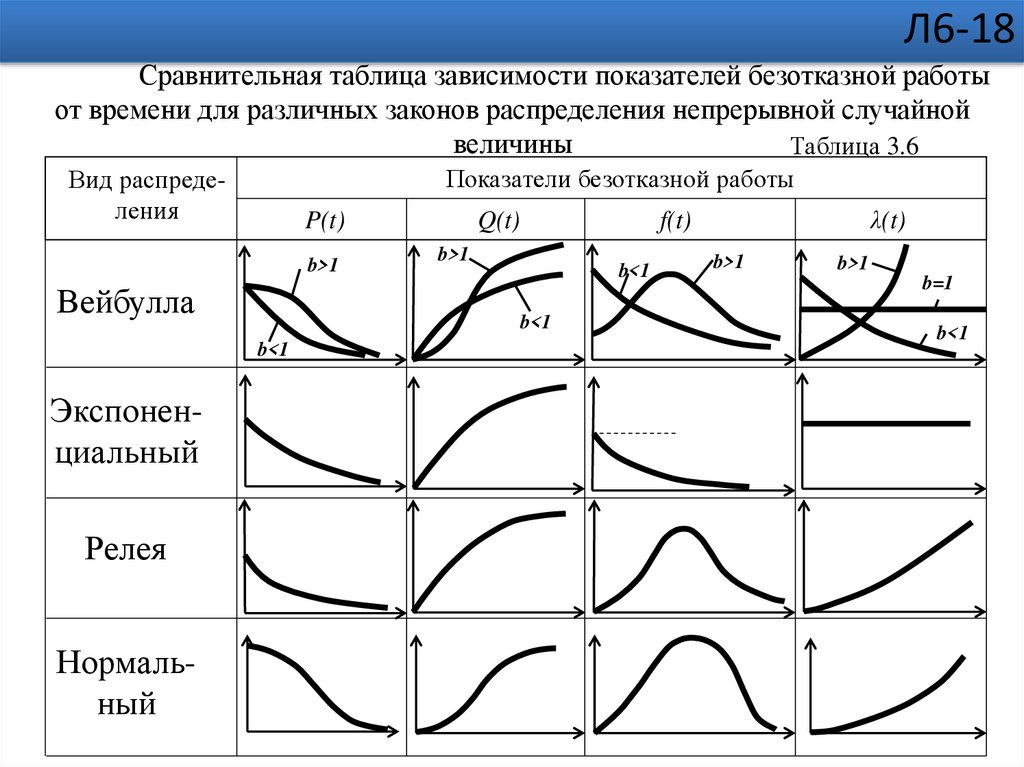
Л6-18
Сравнительная таблица зависимости показателей безотказной работы
от времени для различных законов распределения непрерывной случайной
величины
Таблица 3.6
Показатели безотказной работы
Вид распределения
P(t)
b>1
Вейбулла
Релея
Нормальный
λ(t)
f(t)
b>1
b<1
b<1
b<1
Экспоненциальный
Q(t)
b>1
b>1
b=1
b<1

19.

Л6-19
Выводы по законам распределения для
непрерывных случайных величин:
● поведение системы на 1-м участке (участок приработки)
эксплуатации с достаточно высокой точностью описывается
законом распределения Вейбулла (с b<1);
● поведение системы на 2-м участке (участок нормальной
эксплуатации) описывается экспоненциальным законом;
● поведение системы на 3-м участке (участок явно
выраженного
старения
и
износа)
описывается
распределением Релея или Вейбулла (с b>1).

20.

Л6-20

21.

Л6-21

22.

Л6-22
Для применения данного метода должны
выполняться следующие условия:
1) Наличие данных по достаточно большой совокупности
явлений. Обычно полагается, что достаточным будет число
наблюдений в 5-10 раз превосходящее число факторов.
Однако для более точного построения зависимости
желательно превосходство числа наблюдений в десятки ил
сотни раз. В этом случае в полную силу начинает
действовать закон больших чисел.
2) Обеспечение надежного представления выражения
определенной закономерностью. Иногда в качестве
дополнительного условия выдвигают необходимость
подчинения распределения совокупности по
результативному и факторным признакам нормальному
закону распределения, что связано с использованием
метода наименьших квадратов.