Similar presentations:
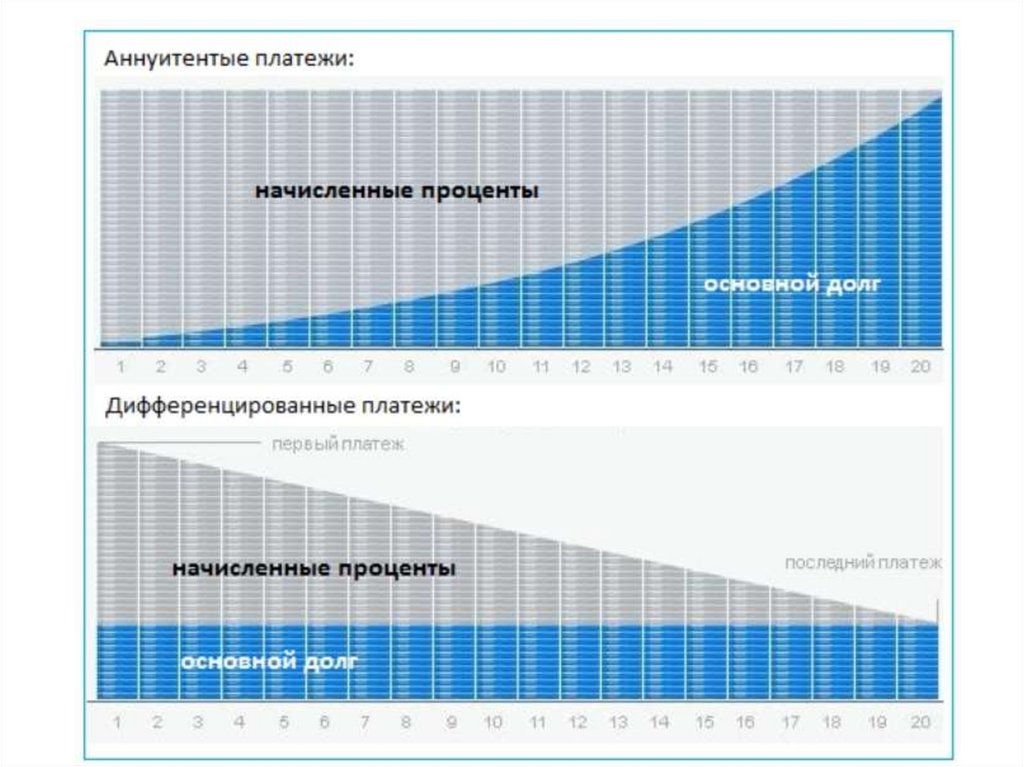
Аннуитетный вид платежа кредита
1.
Семинар №2 -3 по решению экономическихзадач (№15 в тестах ЕГЭ по математике).
Подготовила учитель математики высшей категории ОАНО
«Лидеры» Одинцовского района
Ведерникова И.А.
2.
3.
Задачи с равномерными платежамиДано:
А- сумма взятая в кредит
Х –ежемесячный платеж
n-количество лет, на которое взят кредит
р – количество процентов, под которое
выдан кредит
4.
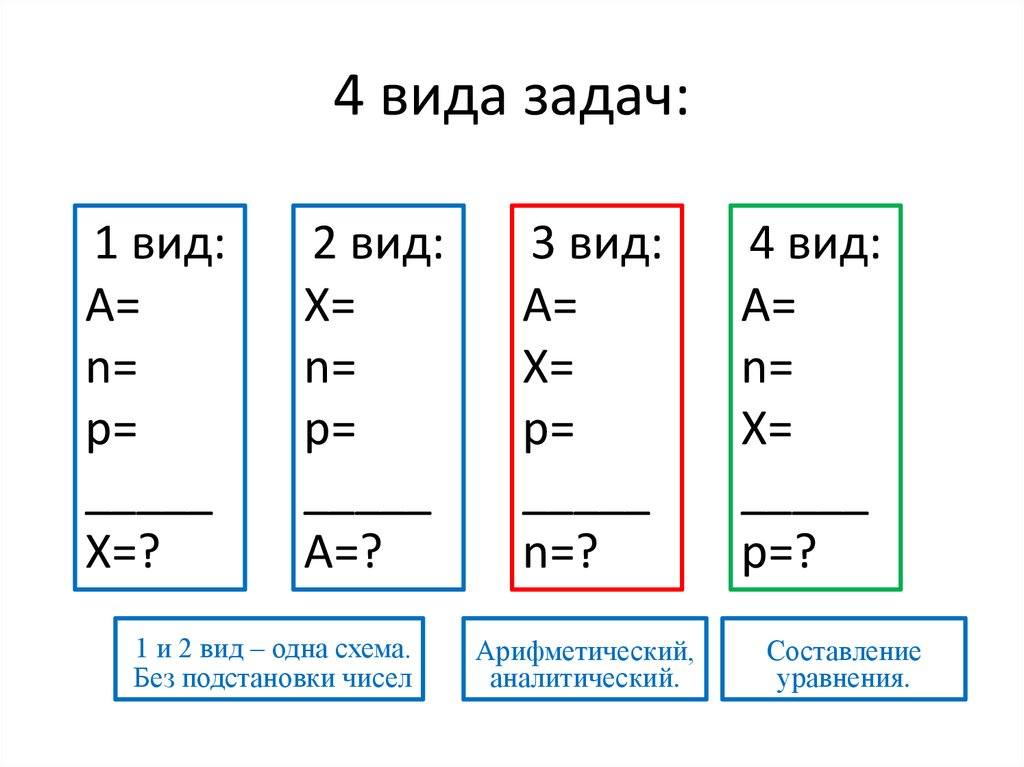
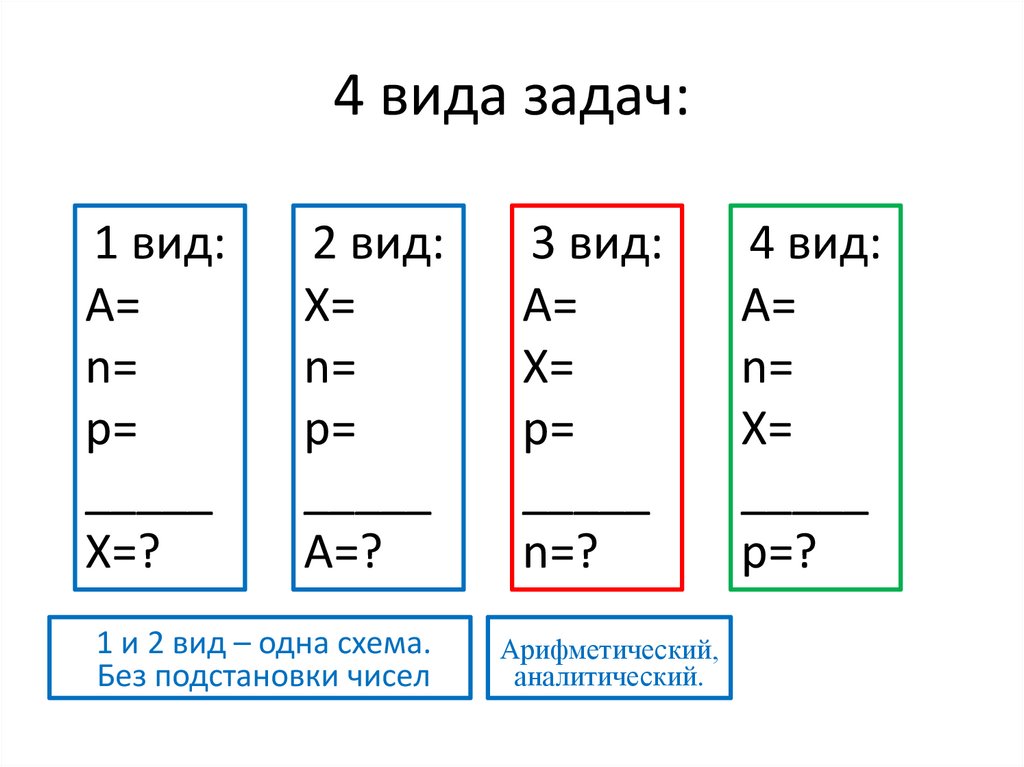
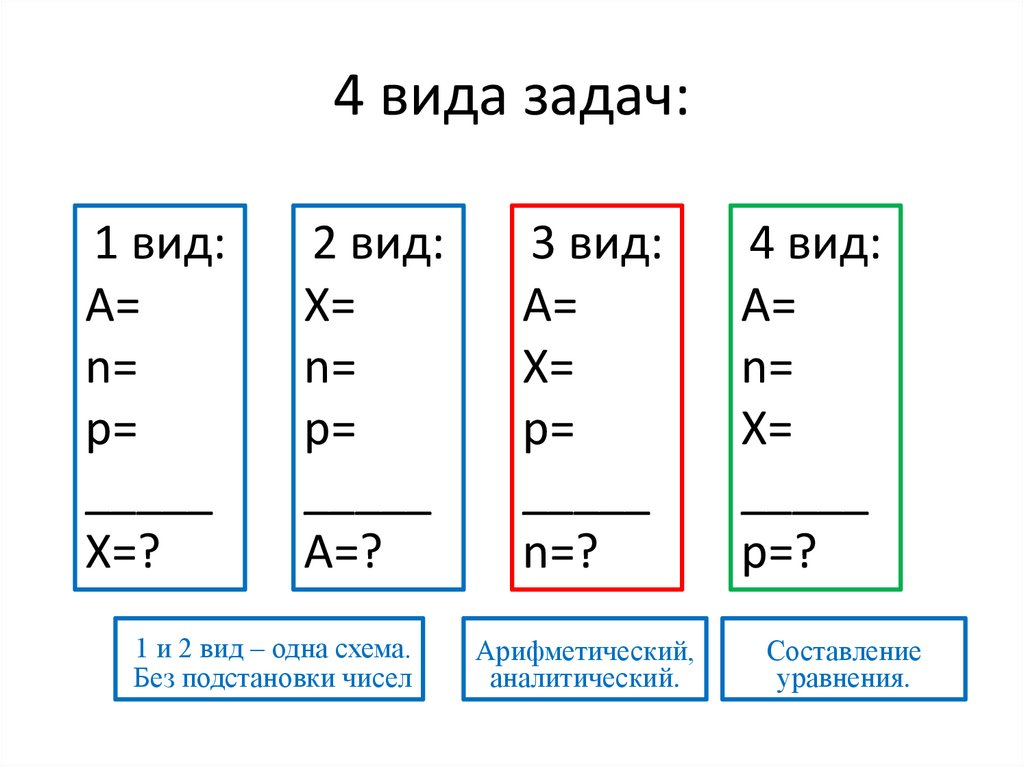
4 вида задач:1 вид:
А=
n=
p=
_____
X=?
2 вид:
Х=
n=
p=
_____
А=?
1 и 2 вид – одна схема.
Без подстановки чисел
.
3 вид:
А=
Х=
p=
_____
n=?
Арифметический,
аналитический.
4 вид:
А=
n=
Х=
_____
р=?
Составление
уравнения.
5.
Задача №1.Разбор видов: 1 и 2 вид – одна схема. Без подстановки чисел.• 31 декабря 2017 года Алексей взял в банке
6 902 000 рублей в
кредит под 12,5% годовых. Схема выплаты кредита следующая —
31 декабря каждого следующего года банк начисляет проценты
на оставшуюся сумму долга (то есть увеличивает долг на 12,5%),
затем Алексей переводит в банк X рублей. Какой должна быть
сумма X, чтобы Алексей выплатил долг четырьмя равными
платежами (то есть за четыре года)?
Дано:
1 вид:
• А= 6 902 000 руб.
А=
• p=12,5%
n=
• n=4 года
• ______
p=
• X=? руб
_____
X=?
6.
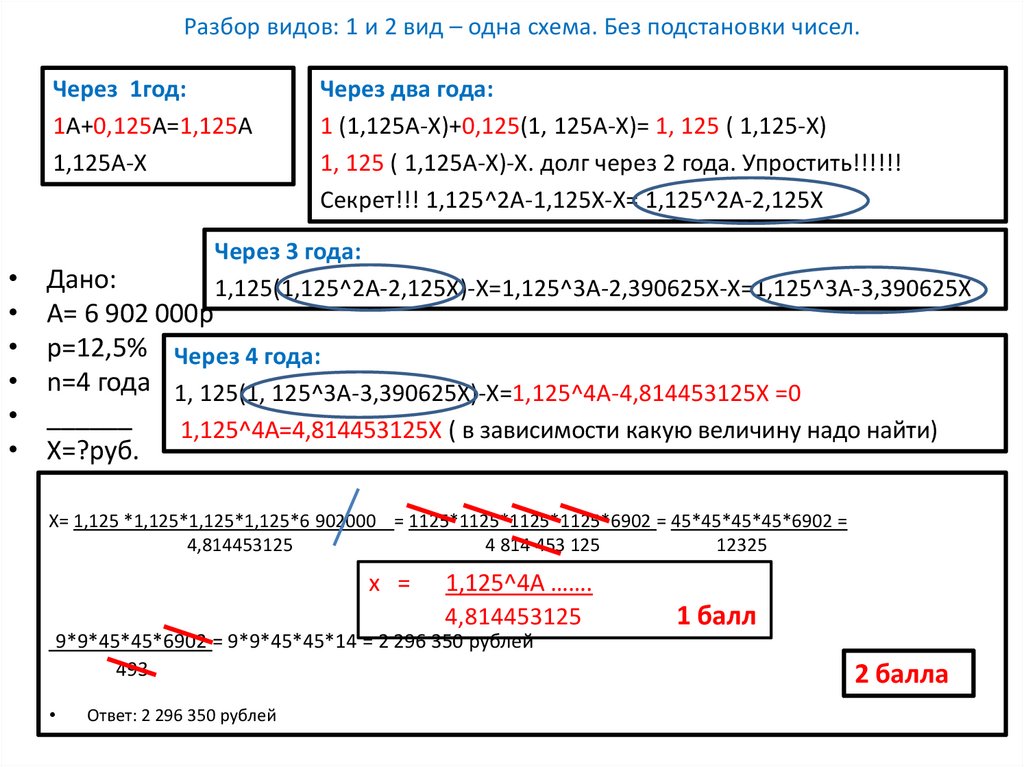
Разбор видов: 1 и 2 вид – одна схема. Без подстановки чисел.Через 1год:
1А+0,125А=1,125А
1,125А-Х
Через два года:
1 (1,125А-Х)+0,125(1, 125А-Х)= 1, 125 ( 1,125-Х)
1, 125 ( 1,125А-Х)-Х. долг через 2 года. Упростить!!!!!!
Секрет!!! 1,125^2А-1,125Х-Х= 1,125^2А-2,125Х
Через 3 года:
1,125(1,125^2А-2,125Х)-Х=1,125^3А-2,390625Х-Х=1,125^3А-3,390625Х
Дано:
А= 6 902 000р
p=12,5% Через 4 года:
n=4 года 1, 125(1, 125^3А-3,390625Х)-Х=1,125^4А-4,814453125Х =0
______
1,125^4А=4,814453125Х ( в зависимости какую величину надо найти)
X=?руб.
Х= 1,125 *1,125*1,125*1,125*6 902000 = 1125*1125*1125*1125*6902 = 45*45*45*45*6902 =
4,814453125
4 814 453 125
12325
х =
1,125^4А …….
4,814453125
9*9*45*45*6902 = 9*9*45*45*14 = 2 296 350 рублей
493
Ответ: 2 296 350 рублей
1 балл
2 балла
7.
Дано:
А= 6 902 000р
p=12,5%
n=4 года
______
X=?руб.
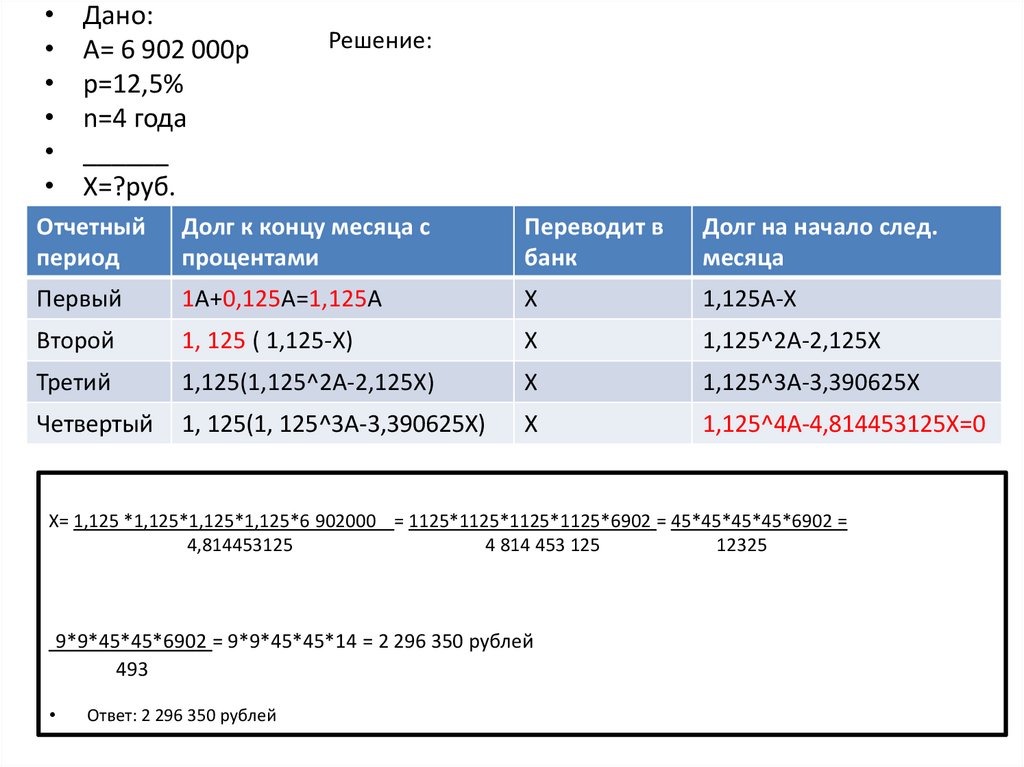
Решение:
Отчетный
период
Долг к концу месяца с
процентами
Переводит в
банк
Долг на начало след.
месяца
Первый
1А+0,125А=1,125А
Х
1,125А-Х
Второй
1, 125 ( 1,125-Х)
Х
1,125^2А-2,125Х
Третий
1,125(1,125^2А-2,125Х)
Х
1,125^3А-3,390625Х
Четвертый
1, 125(1, 125^3А-3,390625Х)
Х
1,125^4А-4,814453125Х=0
Х= 1,125 *1,125*1,125*1,125*6 902000 = 1125*1125*1125*1125*6902 = 45*45*45*45*6902 =
4,814453125
4 814 453 125
12325
9*9*45*45*6902 = 9*9*45*45*14 = 2 296 350 рублей
493
Ответ: 2 296 350 рублей
8.
Формулы для аннуитетныхрасчетов
n- платежные периоды
Sо- сумма кредита
m= 1+0,01р
р%- процентная ставка
Х- постоянные выплаты
Sn-величина текущего долга
9.
Разбор видов: 1 и 2 вид – одна схема. Без подстановки чисел.• 31 декабря 2017 года Алексей взял в банке
6 902 000 рублей в
кредит под 12,5% годовых. Схема выплаты кредита следующая —
31 декабря каждого следующего года банк начисляет проценты
на оставшуюся сумму долга (то есть увеличивает долг на 12,5%),
затем Алексей переводит в банк X рублей. Какой должна быть
сумма X, чтобы Алексей выплатил долг четырьмя равными
платежами (то есть за четыре года)?
Дано:
А= 6 902 000р
p=12,5%
n=4года
______
X=?руб.
Можно!!!! Составить модель.
1,125(1,125(1,125(1,125А-Х)-Х)-Х)-Х=0
Но!!!!! сложно упростить и вычислить!!!!!
1 балл
Можно!!!!!! Воспользоваться формулой
m= 1+0,01р
р%- процентная ставка
Но!!!! Нет вывода модели!!!!!
1 балл
10.
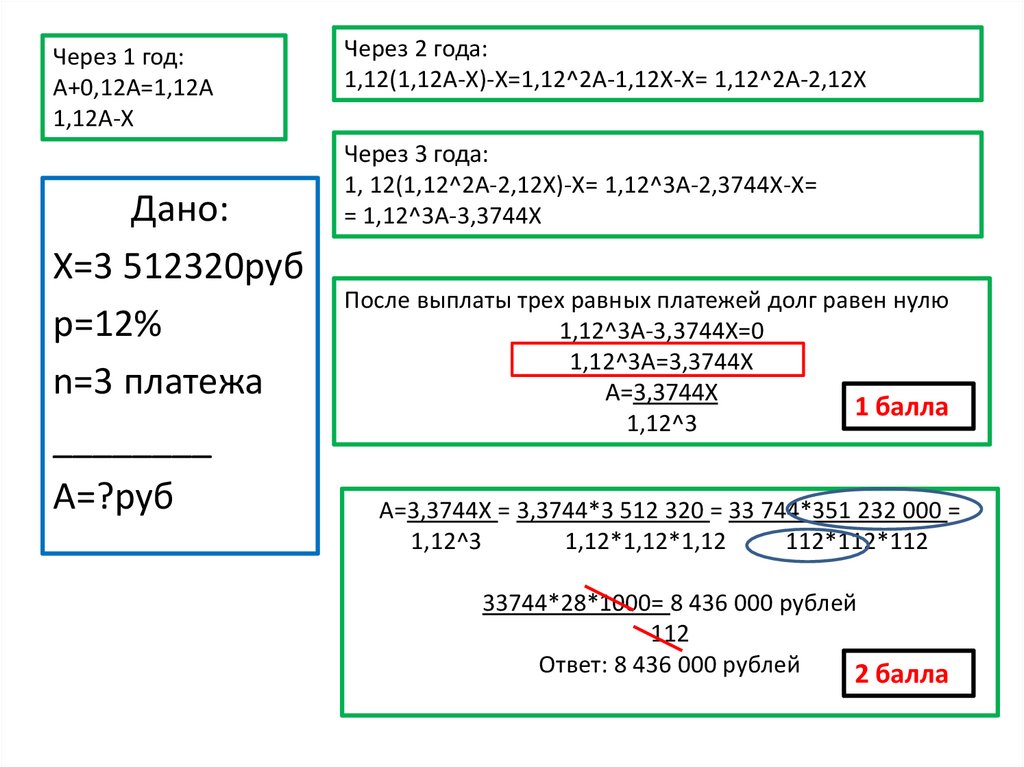
Задача 2. Разбор видов: 1 и 2 вид – одна схема. Без подстановки чисел.Сергей взял в банке некоторую сумму в кредит под 12%
годовых .Какую сумму Сергей взял в банке, если он выплатит
долг тремя равными платежами? Ежегодный платеж по
кредиту составил 3 512 320рублей.
Дано:
Х=3 512 320руб.
р=12%
n=3 платежа
________
А=? руб
2 вид:
Х=
n=
p=
_____
А=?
11.
Через 1 год:А+0,12А=1,12А
1,12А-Х
Дано:
Х=3 512320руб
р=12%
n=3 платежа
________
А=?руб
Через 2 года:
1,12(1,12А-Х)-Х=1,12^2А-1,12Х-Х= 1,12^2А-2,12Х
Через 3 года:
1, 12(1,12^2А-2,12Х)-Х= 1,12^3А-2,3744Х-Х=
= 1,12^3А-3,3744Х
После выплаты трех равных платежей долг равен нулю
1,12^3А-3,3744Х=0
1,12^3А=3,3744Х
А=3,3744Х
1 балла
1,12^3
А=3,3744Х = 3,3744*3 512 320 = 33 744*351 232 000 =
1,12^3
1,12*1,12*1,12
112*112*112
33744*28*1000= 8 436 000 рублей
112
Ответ: 8 436 000 рублей
2 балла
12.
Задача 2. Разбор видов: 1 и 2 вид – одна схема. Без подстановки чисел.Сергей взял в банке некоторую сумму в кредит под 12%
годовых .Какую сумму Сергей взял в банке, если он выплатит
долг тремя равными платежами? Ежегодный платеж по
кредиту составил 3 512 320рублей.
Отчетный
период
Долг к концу месяца
с процентами
Переводит в банк
Долг на начало
следующего
месяца
Первый
А+0,12А=1,12А
Х
1,12А-Х
Второй
1,12^2А-1,12Х
Х
1,12^2А-2,12Х
Третий
1, 12(1,12^2А-2,12Х)
Х
12^3А-3,3744Х =0
13.
4 вида задач:1 вид:
А=
n=
p=
_____
X=?
2 вид:
Х=
n=
p=
_____
А=?
1 и 2 вид – одна схема.
Без подстановки чисел
.
3 вид:
А=
Х=
p=
_____
n=?
Арифметический,
аналитический.
4 вид:
А=
n=
Х=
_____
р=?
14.
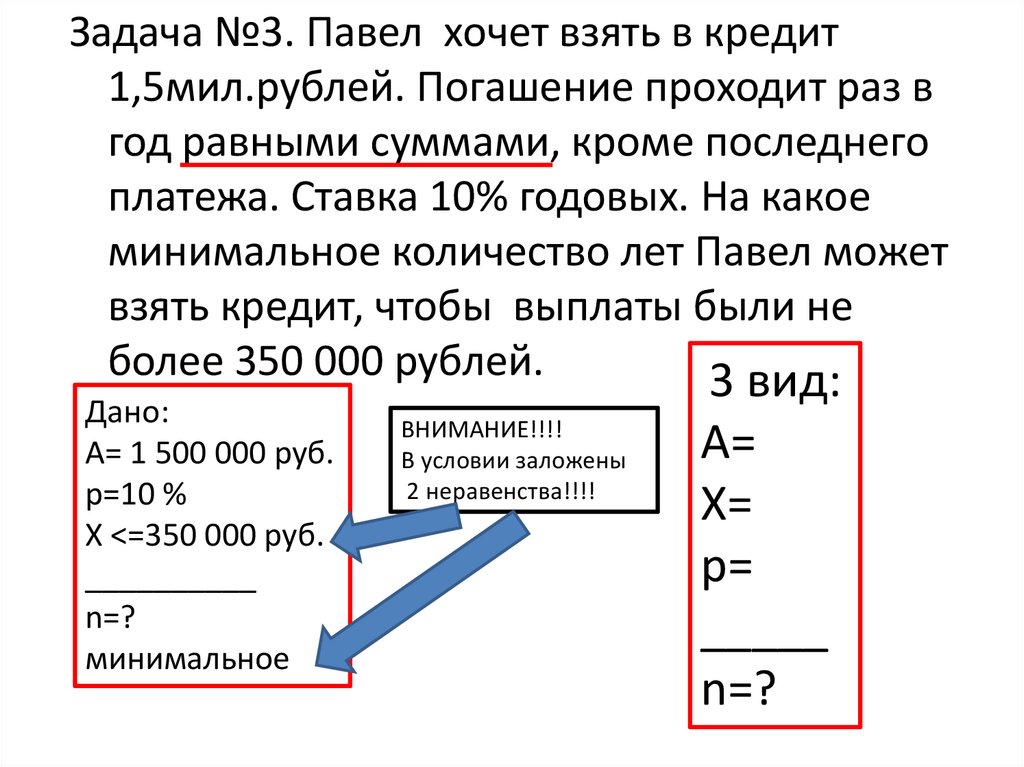
Задача №3. Павел хочет взять в кредит1,5мил.рублей. Погашение проходит раз в
год равными суммами, кроме последнего
платежа. Ставка 10% годовых. На какое
минимальное количество лет Павел может
взять кредит, чтобы выплаты были не
более 350 000 рублей.
3 вид:
Дано:
А= 1 500 000 руб.
р=10 %
Х <=350 000 руб.
__________
n=?
минимальное
ВНИМАНИЕ!!!!
В условии заложены
2 неравенства!!!!
А=
Х=
p=
_____
n=?
15.
(Арифметический способ)Решение: Словесное описание модели.
Так как в условии задачи прописана
аннуитетная схема выплат кредита, на
Дано:
что указывает во первых- погашение
А= 1 500 000 руб.
кредита равными платежами, а во
р=10 %
вторых - начисление процентов
Х <=350 000 руб.
происходит, в начале каждого года на
оставшуюся сумму, и опираясь на
__________
условие задачи , где можно заметить,
n=?
что известны все данные, то есть
минимальное
известны: сумма взятая в кредит,
ежегодная процентная ставка и платеж,
то количество периодов можно
просчитать арифметическим способом.
Остается посчитать количество этих
периодов.
16.
Решение: (арифметический способ)Для того, что бы число лет было минимальным, платить надо по максимуму.
Пусть Павел платит 350 000 рублей.
Через 1 год после
начисления %:
1 500 000
+ 150 000
1 650 000
Через 1 год после
выплаты платежа:
1 650 000
- 350 000
1 300 000
Через 4 года:
838 000
+ 83 800
921 800
Через 2 года после
начисления %:
1 300 000
+ 130 000
1 430 000
Через 2 года после
начисления %:
1 430 000
- 350 000
1 080 000
Через 5 лет:
571 800
+ 57 180
628 980
Через 3 года после
начисления %:
1 080 000
+ 108 000
1 188 000
Через 2 года после
начисления %:
1 188 000
- 350 000
838 000
Через 4 года:
921 800
-350 000
571 800
Через 5 лет:
628 980
+350 000
278 980
Останавливаться нельзя!!!!
Через 6 года:
278 980
+ 27 898
306 878
Меньше 350 000
Ответ: 6 лет
17.
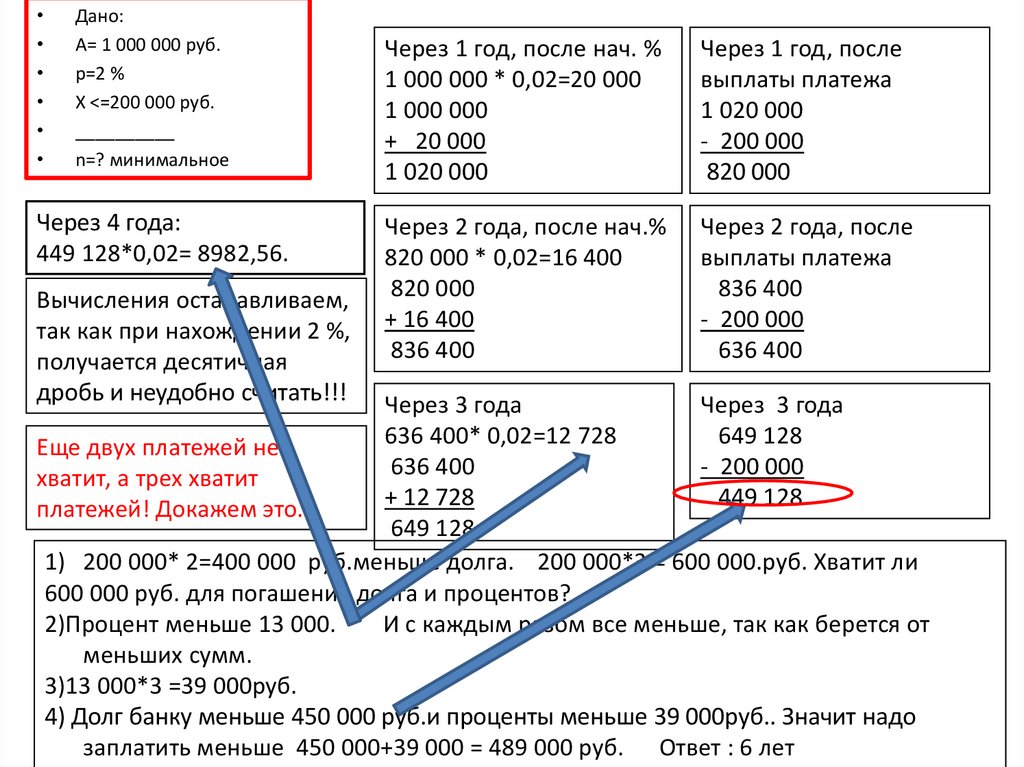
• Задача №4. Андрей взял в банке 1 миллионрублей в кредит. Погашение проходит раз в
год одинаковыми суммами (кроме может
быть последнего) после начисления
процентов. Ставка - 2% годовых. На какое
минимальное количество лет может Андрей
взять кредит, чтобы ежегодные выплаты были
не более 200 000 рублей?
Дано:
А= 1 000 000 руб.
р=2 %
Х <=200 000 руб.
__________
n=?
минимальное
Решение
смешанное:
арифметическое и
аналитическое.
3 вид:
А=
Х=
p=
_____
n=?
18.
Дано:
А= 1 000 000 руб.
р=2 %
Х <=200 000 руб.
__________
n=? минимальное
Через 4 года:
449 128*0,02= 8982,56.
Вычисления останавливаем,
так как при нахождении 2 %,
получается десятичная
дробь и неудобно считать!!!
Через 1 год, после нач. %
1 000 000 * 0,02=20 000
1 000 000
+ 20 000
1 020 000
Через 1 год, после
выплаты платежа
1 020 000
- 200 000
820 000
Через 2 года, после нач.%
820 000 * 0,02=16 400
820 000
+ 16 400
836 400
Через 2 года, после
выплаты платежа
836 400
- 200 000
636 400
Через 3 года
Через 3 года
636 400* 0,02=12 728
649 128
Еще двух платежей не
636 400
- 200 000
хватит, а трех хватит
+ 12 728
449 128
платежей! Докажем это.
649 128
1) 200 000* 2=400 000 руб.меньше долга. 200 000*3 = 600 000.руб. Хватит ли
600 000 руб. для погашения долга и процентов?
2)Процент меньше 13 000.
И с каждым разом все меньше, так как берется от
меньших сумм.
3)13 000*3 =39 000руб.
4) Долг банку меньше 450 000 руб.и проценты меньше 39 000руб.. Значит надо
заплатить меньше 450 000+39 000 = 489 000 руб. Ответ : 6 лет
19.
Аналитическое решение задачиДано:
А= 1 000 000 руб.
р=2 %
Х <=200 000 руб.
__________
n=?
минимальное
Через 1 год
1 000 000 * 0,02=20 000 руб.
проценты далее будут уменьшатся.
В 1 000 000руб. вмещается 5 раз по 200 000руб.
5 платежей не хватит, а 6 платежей хватит!!!
Докажем это!!!
5 платежей мало. 200 000*5 = 1 000 000руб., НО! Еще платить проценты.
6 платежей хватит. Надо: 200 000*6 = 1 200 000руб.,
Проценты меньше 20 000*6 = 120 000руб.
Долг банку меньше 1 000 000+120 000 = 1 120 000руб.
Значит, 1 200 000руб. хватит на оплату кредита.
Ответ: 6 платежей.
20.
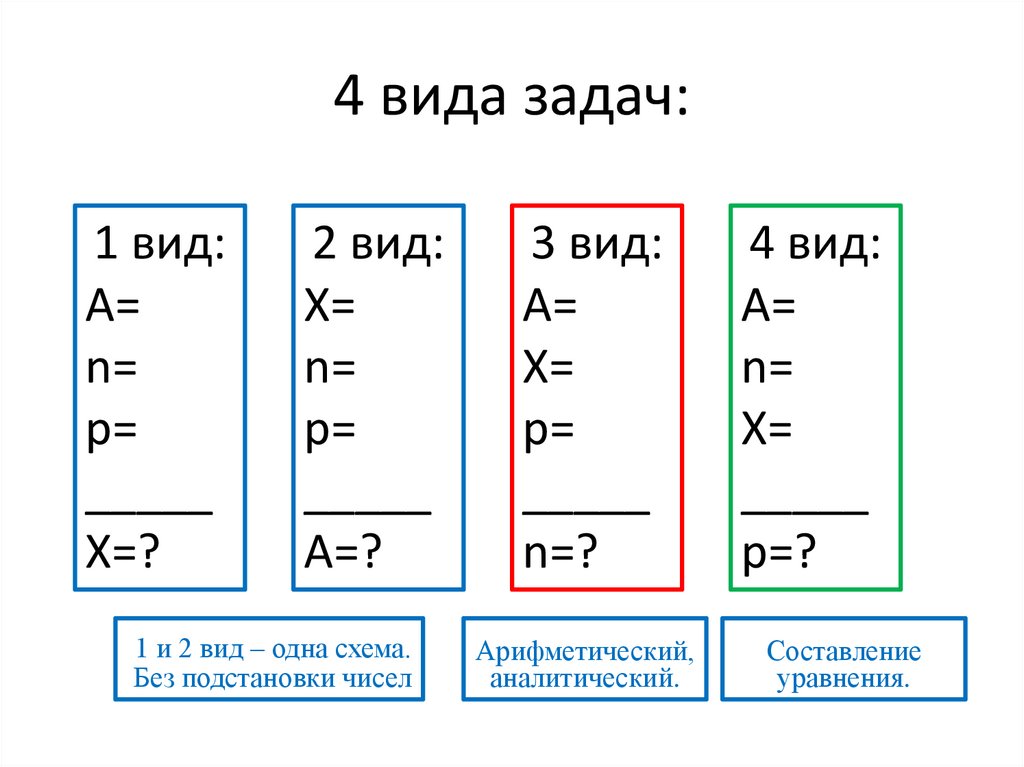
4 вида задач:1 вид:
А=
n=
p=
_____
X=?
2 вид:
Х=
n=
p=
_____
А=?
1 и 2 вид – одна схема.
Без подстановки чисел
.
3 вид:
А=
Х=
p=
_____
n=?
Арифметический,
аналитический.
4 вид:
А=
n=
Х=
_____
р=?
Составление
уравнения.
21.
• Задача № 5.31 декабря Василий взял кредит на 1 000 000 рублей.
Схема выплат кредита следующая: 31 декабря каждого
следующего года банк начисляет проценты на
оставшуюся сумму долга ( то есть увеличивает долг на
определенное число процентов)затем Василий
переводит очередной транш. Василий выплатил кредит
за два транша, переводя в первый раз 660 тыс. рублей,
а во второй раз 484 тыс.рублей. Под какой процент банк
выдал кредит?
Дано:
А=1 000 000 руб.
n= 2 года
Х1= 660 000 руб.
Х2= 484 000 руб.
___________
Р=? %
4 вид:
А=
n=
Х=
_____
р=?
22.
1 способ:
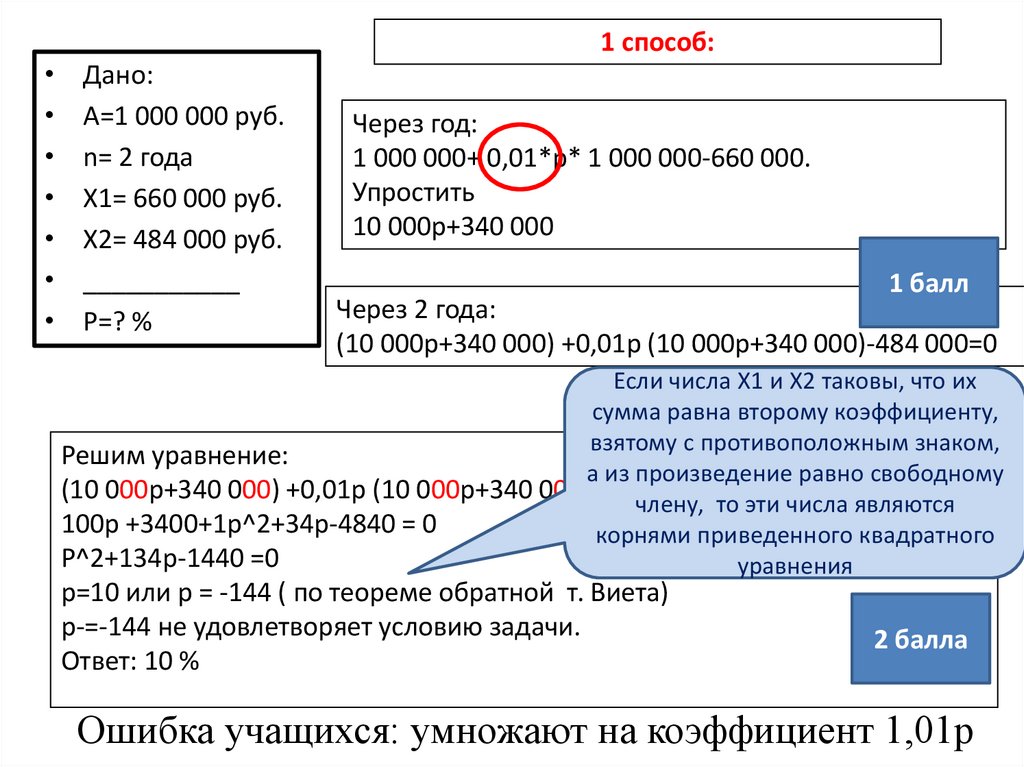
Дано:
А=1 000 000 руб.
n= 2 года
Х1= 660 000 руб.
Х2= 484 000 руб.
___________
Р=? %
Через год:
1 000 000+ 0,01*р* 1 000 000-660 000.
Упростить
10 000р+340 000
1 балл
Через 2 года:
(10 000р+340 000) +0,01р (10 000р+340 000)-484 000=0
Если числа Х1 и Х2 таковы, что их
сумма равна второму коэффициенту,
взятому с противоположным знаком,
Решим уравнение:
а из произведение равно свободному
(10 000р+340 000) +0,01р (10 000р+340 000)-484члену,
000=0то/100
эти числа являются
100р +3400+1р^2+34р-4840 = 0
корнями приведенного квадратного
Р^2+134р-1440 =0
уравнения
р=10 или р = -144 ( по теореме обратной т. Виета)
р-=-144 не удовлетворяет условию задачи.
Ответ: 10 %
2 балла
Ошибка учащихся: умножают на коэффициент 1,01р
23.
Дано:
А=1 000 000 руб.
n= 2 года
Х1= 660 000 руб.
Х2= 484 000 руб.
___________
Р=? %
Вернемся к замене.
а= 1+0,01р
1+0,01р=1,1
0,01р=0,1
Р=10 (%)
Ответ: 10 % 2 балла
2 способ:
10 %
15%
4%
Р%
Числовой множитель
1,1
1,15
1,04
1+0,01р
Обозначим величину 1+0,01р = а,
Тогда через 1 год :
а* 1000 000-660 000=1000 000а-660 000
Через 2 года:
а( 1000 000а-660 000)-484 000=0 /1000
1000а^2-660а-484=0
1 балл
1000а^2-660а-484=0
D1 = 330^2+1000*484=108 900+484000=592 900
=770^2
а = (330-770)/1000= -440/1000 ( не уд.усл.задачи)
или
а = (330+770)/1000= 1100/1000=1,1
24.
4 вида задач:1 вид:
А=
n=
p=
_____
X=?
2 вид:
Х=
n=
p=
_____
А=?
1 и 2 вид – одна схема.
Без подстановки чисел
.
3 вид:
А=
Х=
p=
_____
n=?
Арифметический,
аналитический.
4 вид:
А=
n=
Х=
_____
р=?
Составление
уравнения.
25.
Задачи.Вариант 3.Вариант 4.Вариант 5. Вариант 21.Вариант 22. Вариант 43.
Сборник по подготовке к ЕГЭ -2022
• 31 декабря 2016 года Василий взял в банке
5 460 000 рублей в кредит под 20% годовых.
Схема выплаты кредита следующая – 31
декабря каждого следующего года банк
начисляет проценты на оставшуюся сумму
долга (то есть увеличивает долг на 20%),
затем Василий переводит в банк Х рублей.
Какой должна быть сумма Х , чтобы
Василий выплатил долг тремя равными
платежами ( то есть за три года)?
26.
Задача.Вариант 28. Вариант 29. вариант 30. Вариант 27.
Сборник по подготовке к ЕГЭ -2022
• Планируется выдать льготный кредит на целое
число миллионов рублей на 4 года.В середине
каждого года действия кредита долг заемщика
возрастает на 20% по сравнению с началом года. В
конце 1-го и 2 –го годов заемщик выплачивает
только проценты по кредиту, оставляя долг
неизменно равным первоначальному. В конце 3
года и 4 –го годов заемщик выплачивает
одинаковые суммы, погашая весь долг полностью.
Найдите наибольший размер кредита , при
котором общая сумма выплат заемщика будет
меньше 10 млн.рублей.
27.
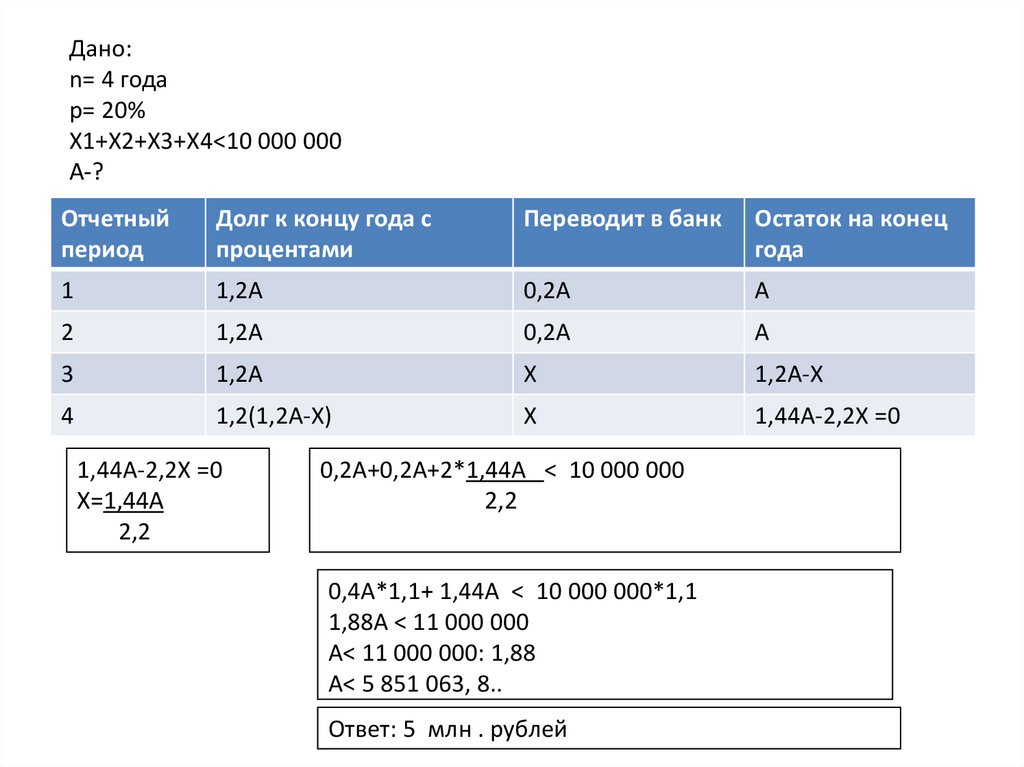
Дано:n= 4 года
р= 20%
Х1+Х2+Х3+Х4<10 000 000
А-?
Отчетный
период
Долг к концу года с
процентами
Переводит в банк
Остаток на конец
года
1
1,2А
0,2А
А
2
1,2А
0,2А
А
3
1,2А
Х
1,2А-Х
4
1,2(1,2А-Х)
Х
1,44А-2,2Х =0
1,44А-2,2Х =0
Х=1,44А
2,2
0,2А+0,2А+2*1,44А < 10 000 000
2,2
0,4А*1,1+ 1,44А < 10 000 000*1,1
1,88A < 11 000 000
A< 11 000 000: 1,88
А< 5 851 063, 8..
Ответ: 5 млн . рублей
















 mathematics
mathematics








