Теорема о прямой, перпендикулярной плоскости. Повторение

1. Теорема о прямой, перпендикулярной плоскости

Выполнила
Теорема о прямой,
перпендикулярной
плоскости

2.

Повторим теорию.
1. Если прямая перпендикулярна двум пересекающимся
прямым лежащим в плоскости, то она перпендикулярна к
этой плоскости.
2. Если одна из двух параллельных прямых
перпендикулярна к плоскости, то и другая прямая
перпендикулярна к этой плоскости.
3. Прямая называется перпендикулярной плоскости, если
она перпендикулярна к любой прямой , лежащей в этой
плоскости
4. Если две прямые перпендикулярны к плоскости, то они
параллельны.

3.

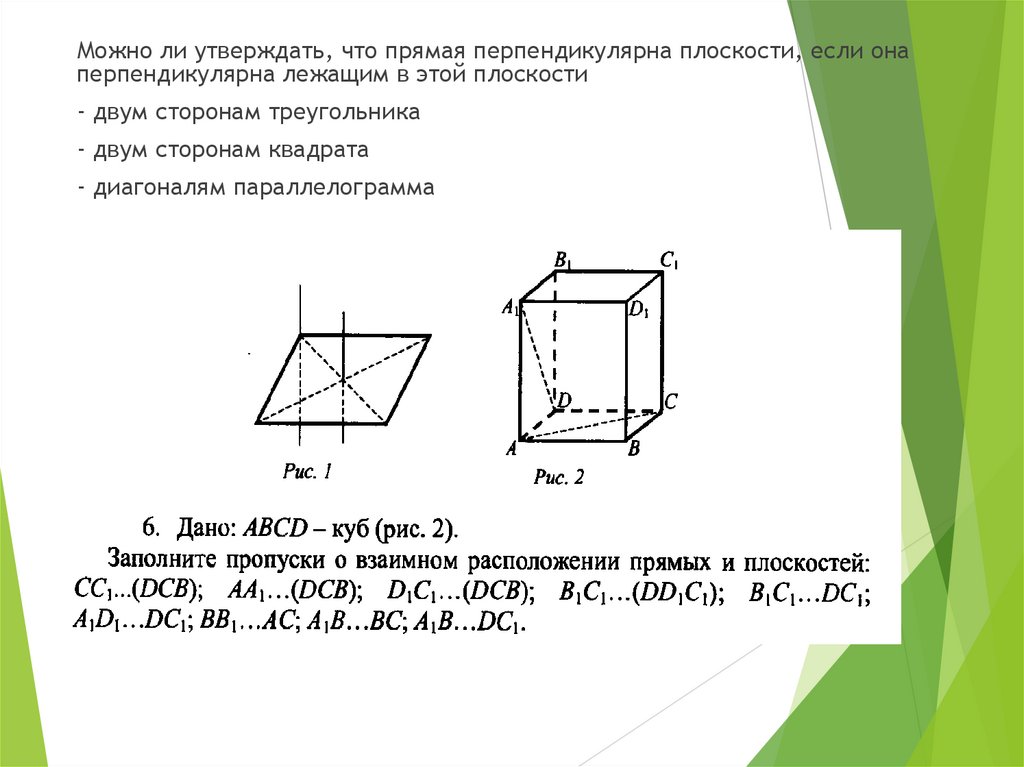
Можно ли утверждать, что прямая перпендикулярна плоскости, если она
перпендикулярна лежащим в этой плоскости
- двум сторонам треугольника
- двум сторонам квадрата
- диагоналям параллелограмма

4.

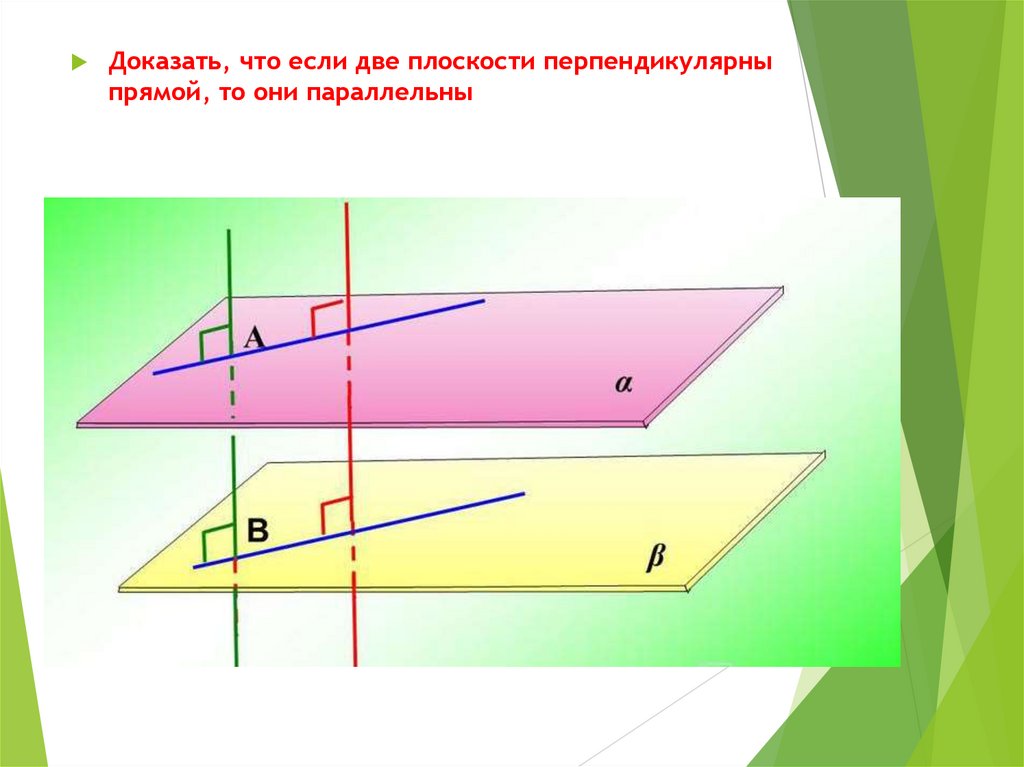
Доказать, что если две плоскости перпендикулярны
прямой, то они параллельны

5.

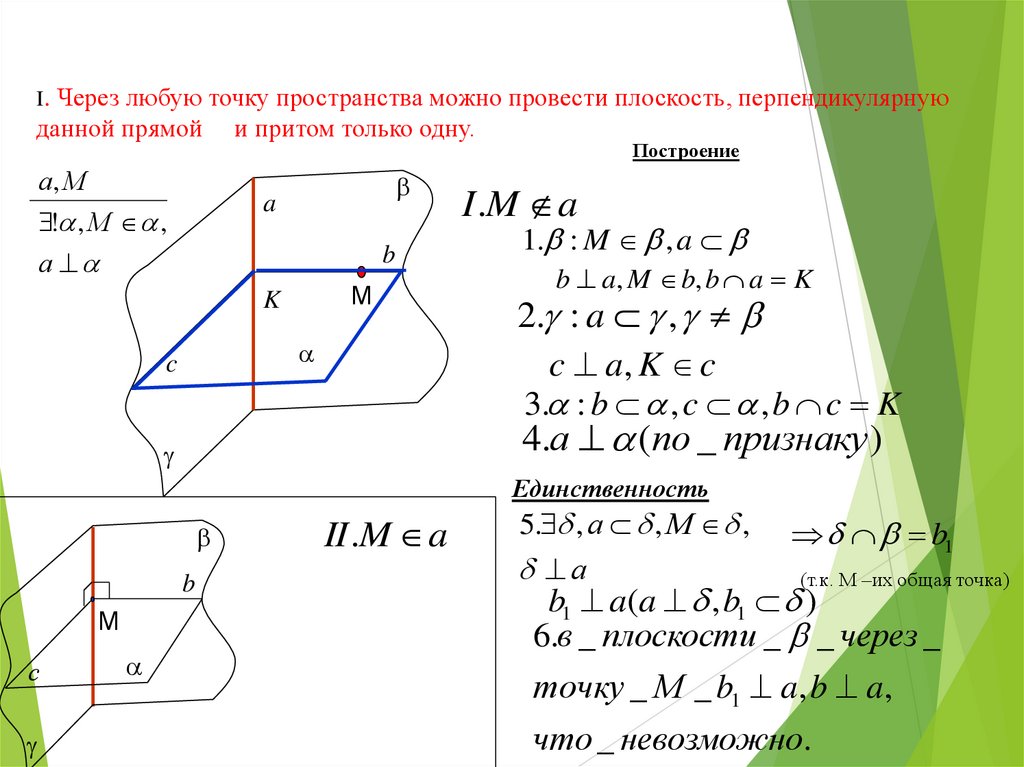
Через любую точку пространства можно провести плоскость, перпендикулярную
данной прямой и притом только одну.
I.
Построение
а, М
a
! , М ,
а
b
М
K
c
I .M a
1. : M , a
b a, M b, b a K
2. : a ,
c a, K c
3. : b , c , b c K
4.а (по _ признаку )
Единственность
b
М
с
II .M a
5. , а , М ,
b1
а
(т.к. М –их общая точка)
b1 a(a , b1 )
6.в _ плоскости _ _ через _
точку _ М _ b1 a, b a,
что _ невозможно.

6.

II. Через любую точку пространства можно провести прямую, перпендикулярную данной
плоскости
и притом только одну.
Построение
,М
I .M a
! а, М а,
1.а1 , а1
а
2. , М , а1
3. b
4.а, М а, а , а b
5.а _(по _ признаку )
M
b
Единственность
a1
а
6. с, с , М с
7.с
а
а с
а с М
а с

7. Решение задач по готовым чертежам

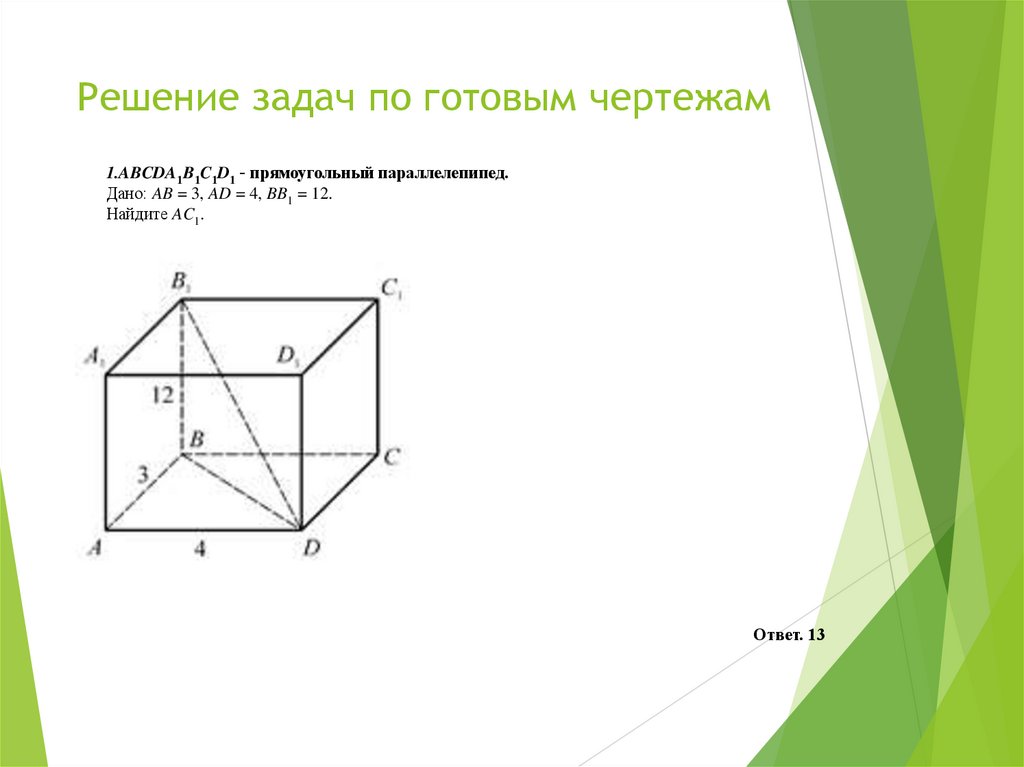
1.ABCDA1B1C1D1 – прямоугольный параллелепипед.
Дано: AB = 3, AD = 4, BB1 = 12.
Найдите AC1.
Ответ. 13

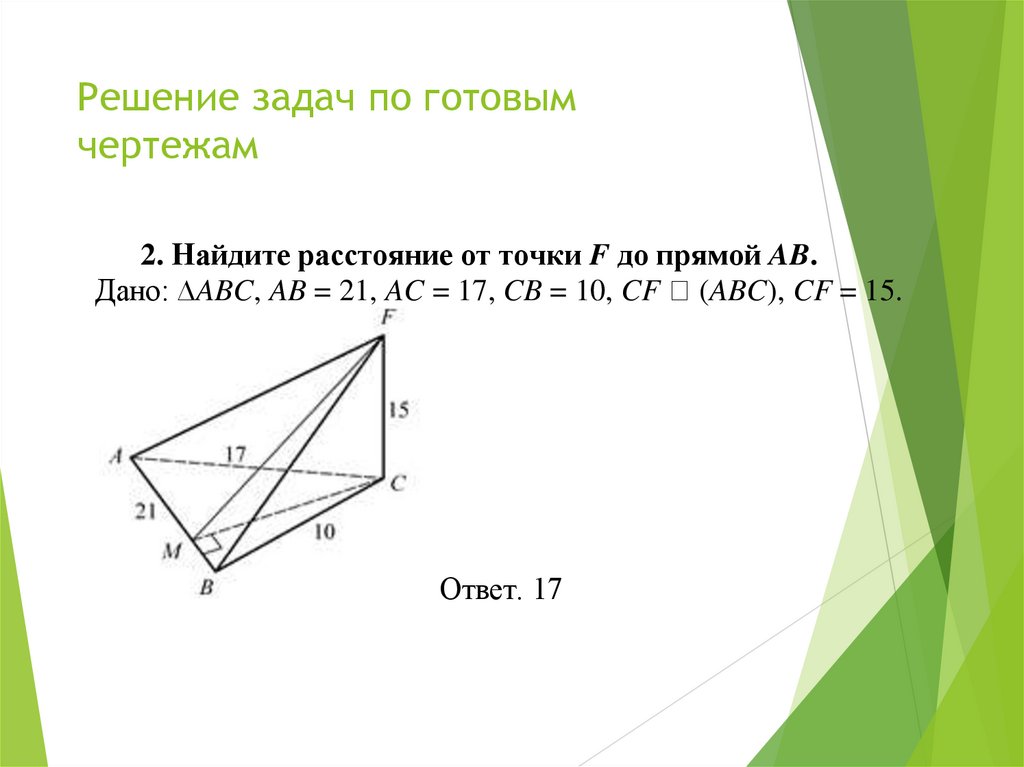
8. Решение задач по готовым чертежам

2. Найдите расстояние от точки F до прямой AB.
Дано: ∆ABC, AB = 21, AC = 17, CB = 10, CF (ABC), CF = 15.
Ответ. 17

9.

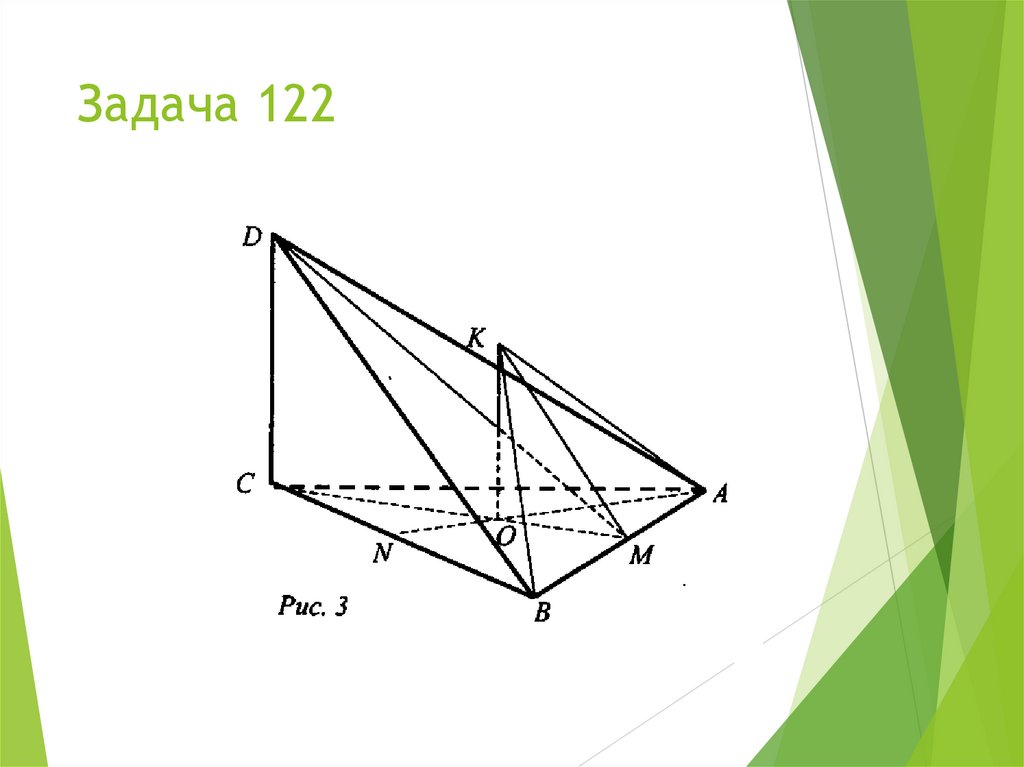
Решение задач.
1. Длина стороны ромба ABCD равна 8 см, длина
диагонали BD равна 12 см. Через точку О пересечения диагоналей
ромба проведена прямая ОК, перпендикулярная его плоскости.
Найдите расстояние от точки К до вершин ромба, если ОК = 14 см.
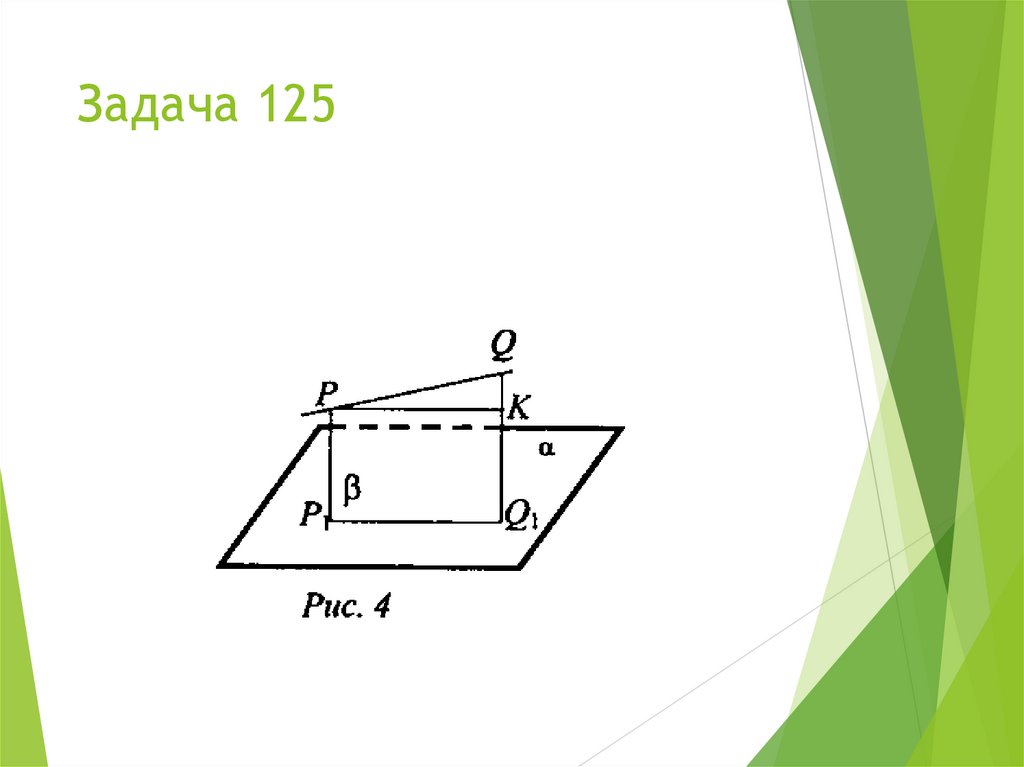
2. Длины сторон треугольника ABC соответственно равны: ВС =
10 см, АВ = 8 см, АС = 4 см. Через сторону АС проведена
плоскость а, составляющая с плоскостью данного треугольника
угол 30°. Найдите расстояние от вершины В до плоскости α.

10. Задача 122

11. Задача 125