Similar presentations:
En küçük kareler yöntemi̇
1.
EN KÜÇÜK KARELER YÖNTEMİMadina Tanikulova 1804.01014
02.05.23
2.
EN KÜÇÜK KARELER YÖNTEMİ• En Küçük Kareler Yöntemi – кээ бир функциялардын
квадраттык четтөөлөрүнүн суммасын керектүү
өзгөрмөлөрдөн минималдаштырууга негизделген ар
кандай маселелерди чечүү үчүн колдонулуучу
математикалык ыкма.
3.
EN KÜÇÜK KARELER YÖNTEMİ• Эң кичине квадраттар методу – үлгү маалыматтарынан
регрессиялык моделдердин белгисиз параметрлерин
баалоо үчүн регрессиялык анализдин негизги
ыкмаларынын бири.
• Ал ошондой эле башка (жөнөкөй) функциялар менен
берилген функцияны болжолдуу көрсөтүү үчүн
колдонулат жана байкоолорду иштетүүдө пайдалуу
болуп чыгат.
4.
5.
ПЛЮСЫ И МИНУСЫEN KÜÇÜK KARELER YÖNTEMİ
• + ал керектүү функциянын a, b, c, ... параметрлерин
аныктоонун салыштырмалуу жөнөкөй математикалык
ыкмасына алып келет;
• + бул ыктымалдык көз караштан алганда жетишээрлик
күчтүү теориялык негиздеме берет.
• - МНКнын негизги кемчилиги – баштапкы
маалыматтарда пайда болгон кескин чектен
чыгууларга карата баалардын сезгичтиги.
6.
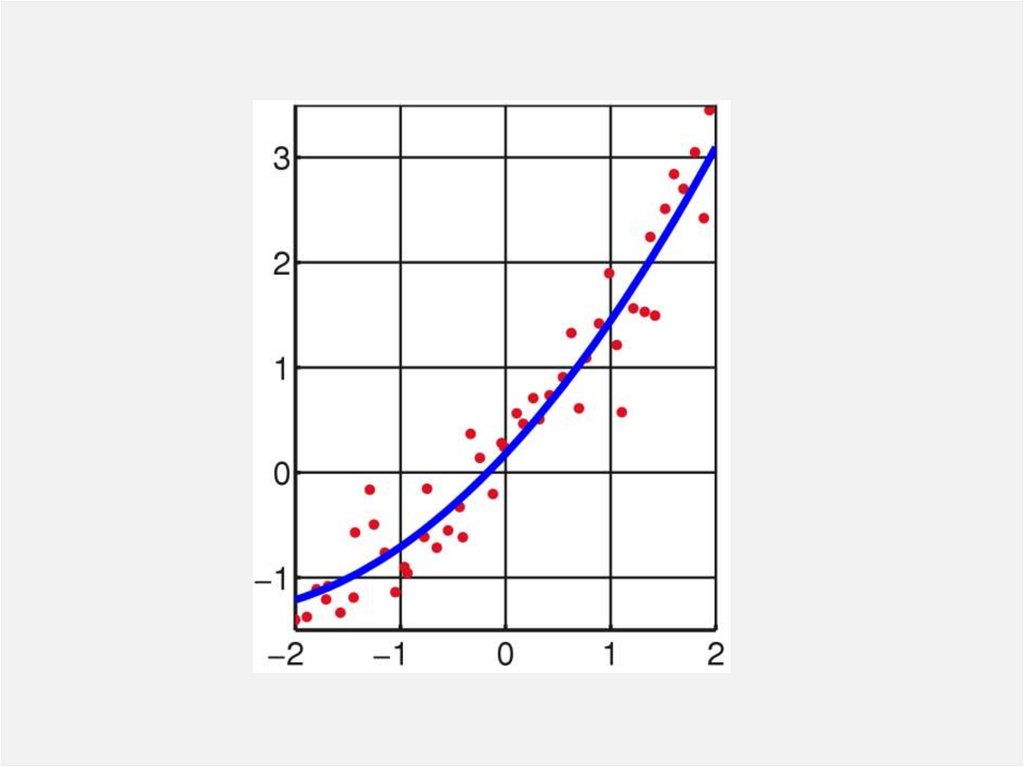
• графиги чекиттерге мүмкүн болушунча жакынөткөн функцияны табышыбыз керек.
• Мындай функция жакындоочу функция
(апроксимация - жакындоо) же теориялык
функция деп аталат.
7.
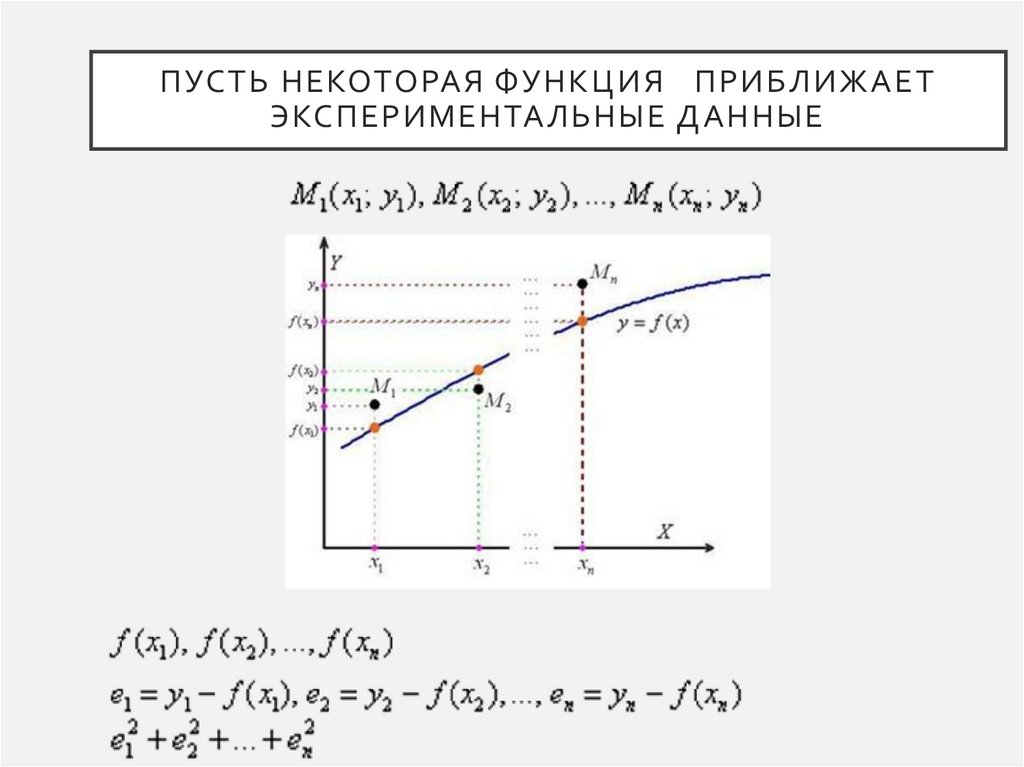
ПУСТЬ НЕКОТОРАЯ ФУНКЦИЯ ПРИБЛИЖАЕТЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
8.
EN KÜÇÜK KARELER YÖNTEMİ9.
EN KÜÇÜK KARELER YÖNTEMİБашка сөз менен айтканда, тапшырма мындай a жана b коэффициенттерин
табуу - квадраттык четтөөлөрдүн суммасы эң аз болушу үчүн.
10.
ВЫВОД ФОРМУЛ ДЛЯ НАХОЖДЕНИЯКОЭФФИЦИЕНТОВ.
11.
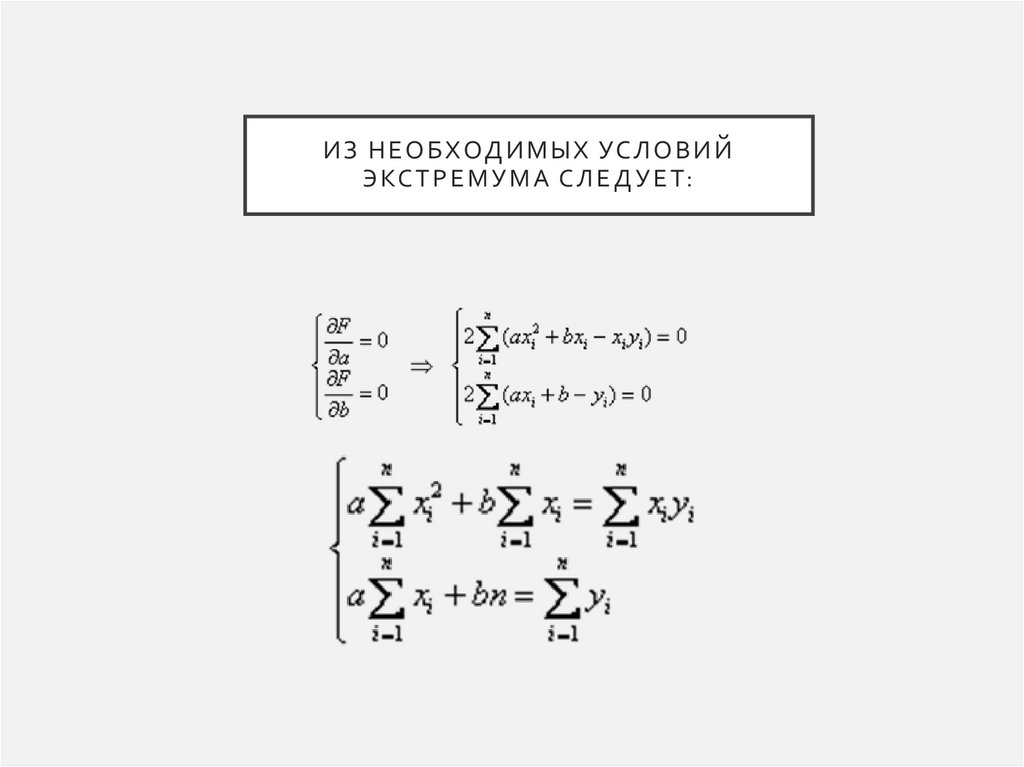
И З Н Е О Б ХОД И М Ы Х УС Л О В И ЙЭ КС Т Р Е М У М А С Л Е Д У Е Т:
12.
АЛГОРИТМ МНК:1)
Находим суммы
2)
Составляем систему уравнений с определённым кол-вом неизвестных.
3)
Решаем систему. (метод Крамера)
4)
В результате получаем стационарную точку S (искомые коэффициенты
a;b)
5)
Вычисляем сумму квадратов отклонений между эмпирическими и
теоретическими значениями.
13.
МИСАЛ• Методом наименьших квадратов найти линейную функцию, которая
наилучшим образом приближает эмпирические (опытные) данные.
14.
МИСАЛ• Коэффициенты a, b оптимальной функции y=ax+b
найдём как решение системы:
15.
.• Таким образом, получаем следующую систему:
16.
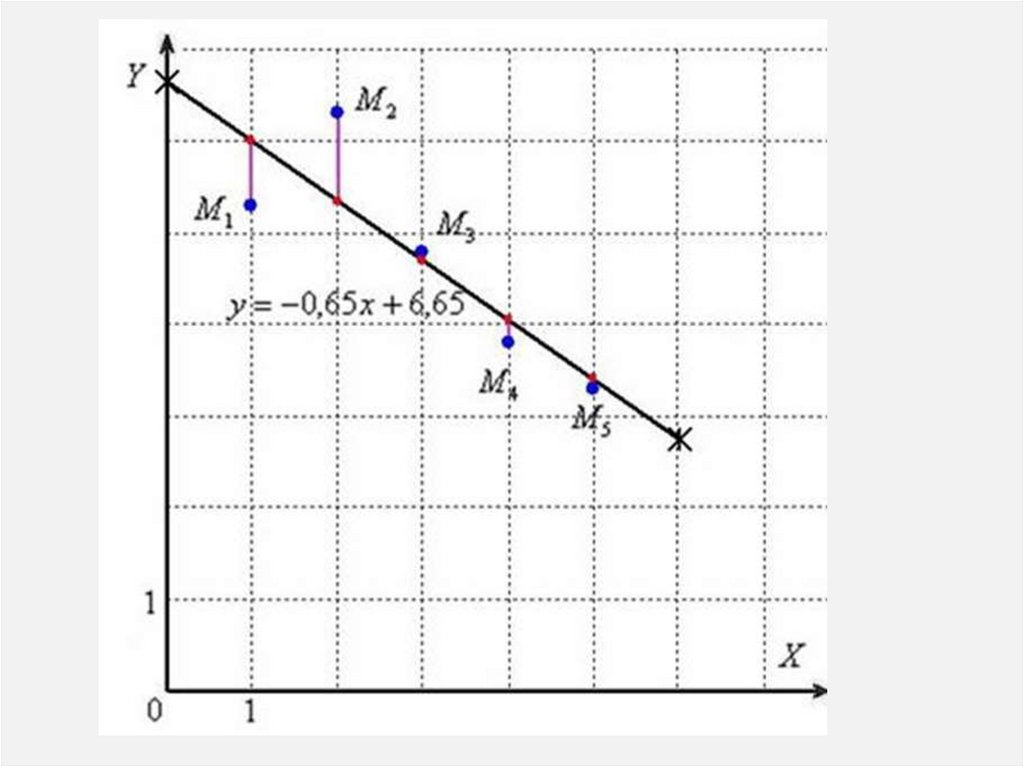
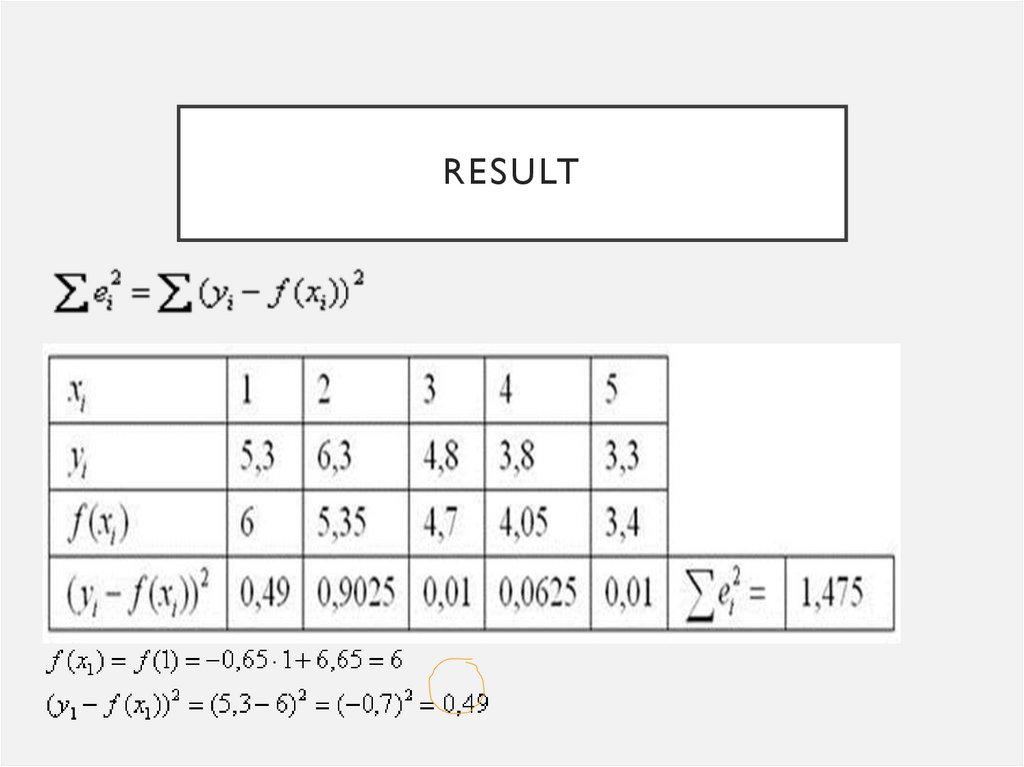
ПРОВЕРКА:Таким образом, искомая аппроксимирующая функция:
Для построения графика аппроксимирующей функции
найдём два её значения:
и выполним чертёж:














 mathematics
mathematics