Similar presentations:
Пример факторного эксперимента для оптимизации свойств исследуемого материала
1.
Пример факторногоэксперимента для оптимизации
свойств исследуемого материала
Цель исследований – получение из отсевов дробления известняков,
укрепленных цементом, экономичных составов для устройства оснований
автомобильных дорог, а также разработка методики подбора
рационального состава
2.
• Исходные данные.• Критерий оптимальности (параметра оптимизации Y) - прочность
материала в МПа.
• Вяжущее - портландцемент М 400 Ульяновского цементного
завода.
• Цель - изучить влияние основных структурообразующих факторов
на формирование прочности исследуемых составов.
• Реализован двухфакторный план эксперимента для создания
математической модели прочности Y.
• Наиболее важные структурообразующие факторы, влияющие на
формирование прочности составов: содержание цемента и
удельное давление при формовании.
• Образцы твердели в нормальных условиях 28 суток, затем
определялась их прочность при сжатии.
3.
• Предположен для реализации двухфакторный план эксперимента с получениеммодели в виде полинома 2-й степени, который имеет вид Y = bo + b1X1 + b2X2 +
b11X12 + b22X22 + b12X1X2 , где bi – регрессионные коэффициенты; Хj –
кодированные значения переменных факторов.
• Уровни варьирования и характеристики изменяемых факторов.
• Кодированные значения факторов связаны с натуральными следующим
соотношением:
• где хi – кодированное значение фактора; Xi – натуральное значение фактора;
X0i – основной уровень фактора Xi; дельтаi – интервал варьирования фактора Xi
4.
• I. Проверка гипотезы об однородности дисперсий по критериюКохрена.
• В каждой точке q плана воспроизводилось пять измерений n = 5.
Количество опытов N = 9.
• Среднее арифметическое вычисляется по формуле
• Дисперсия измерения вычисляется по формуле
• Находим сумму дисперсий по 9 опытам.
• Критерий равен отношению наибольшей из дисперсий к сумме
их всех:
5.
При альфа = 0,05, n = 9 (количество опытов)f2 = m ‒ 1 = 3 – 1 = 2, Gтабл =
При альфа = 0,05, n = 9 (количество опытов) f2 = m ‒ 1 = 5 – 1 = 4,
Gтабл =
6.
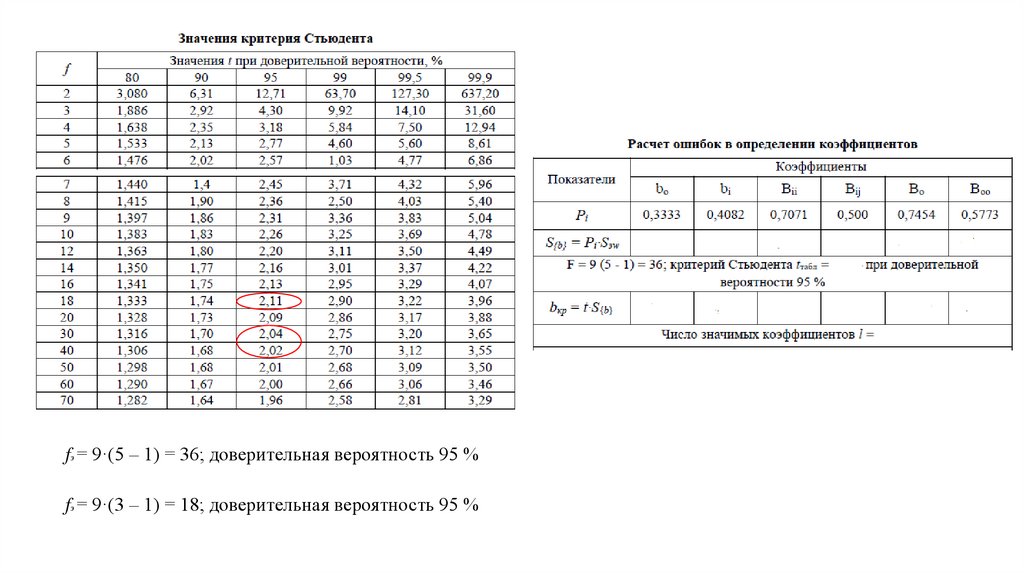
• II. Проверка значимости коэффициентов по критерию Стьюдента.• Расчет оценок коэффициентов регрессии проведем по средним
значениям отклика.
• Определим по вертикальным графам суммы. Далее определим
коэффициенты регрессии.
• В результате получается модель, которую называют начальной.
• При подтверждении гипотезы однородности дисперсий дисперсия
воспроизводимости эксперимента находится усреднением по формуле
среднего арифметического, где m – число опытов в строке.
• Ошибка эксперимента составит
• Если bкр больше соответствующей оценки коэффициента модели, то
истинный коэффициент равен нулю с риском альфа.
где t – критерий Стьюдента для выбранного уровня
значимости
7.
fэ = 9·(5 – 1) = 36; доверительная вероятность 95 %fэ = 9·(3 – 1) = 18; доверительная вероятность 95 %
8.
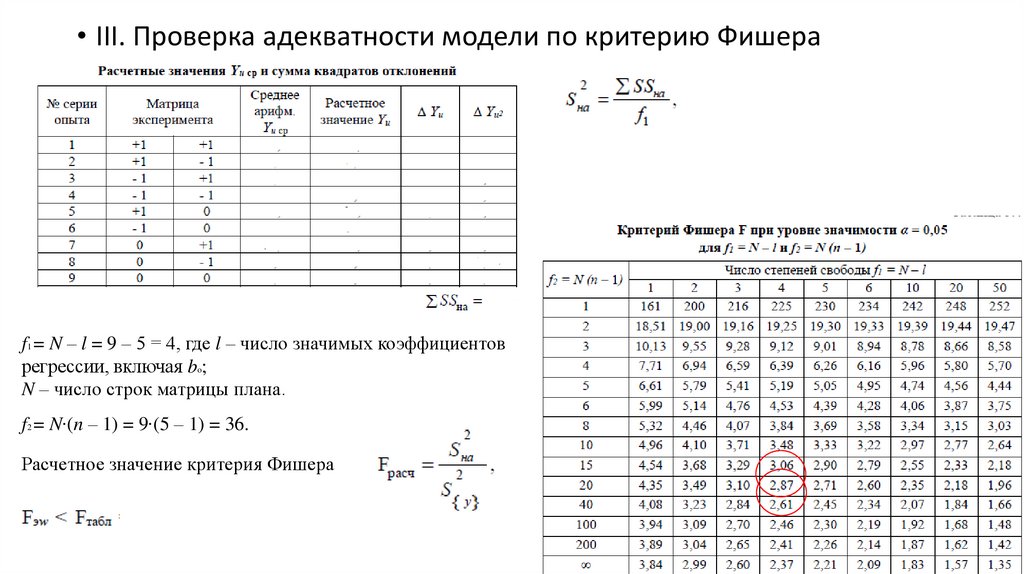
• III. Проверка адекватности модели по критерию Фишераf1 = N – l = 9 – 5 = 4, где l – число значимых коэффициентов
регрессии, включая bo;
N – число строк матрицы плана.
f2 = N∙(n – 1) = 9∙(5 – 1) = 36.
Расчетное значение критерия Фишера






 mathematics
mathematics








