Similar presentations:
Аэродинамические характеристики тел вращения. Тема 9
1.
ОСНОВЫ АЭРОДИНАМИКИЛЕКЦИЯ № 10
Тема 9
Аэродинамические характеристики тел
вращения
2.
Л № 10 Рассматриваемые вопросы2
10.1 Геометрические характеристики тел
вращения.
10.2 Распределение давления по поверхности тела
вращения.
10.3 Аэродинамические характеристики тел
вращения.
10.4 Донное сопротивление.
Литература:
1. Гарбузов В. М., Ермаков А. Л., Кубланов М. С., Ципенко В. Г.
Аэромеханика: Учебник для студентов вузов гражданской авиации – М.:
МГТУГА, 2000, 288 с.
2. Логвинов И. И. Аэромеханика: Учебное пособие М. Иркутск:
ИГТУ, 1998, 144 с.
3. Ништ М. И. Аэродинамика летательных аппаратов. Учебник для ВУЗов.
М.: ВВИА им. проф. Н. Е. Жуковского, 1994, 570 с.
3.
310.1 Геометрические характеристики тел вращения
10.1.1 Основные виды поверхностей ВС:
у1
плоские несущие поверхности:
z1
• крыло;
• горизонтальное оперение;
• вертикальное оперение;
• рулевые поверхности:
х1
высоты (тангажа);
Образующая
направления;
крена;
• закрылки;
• щитки тормозные и спойлеры...
тела вращения: Дать определение
фюзеляж с его цилиндрической и конической частями;
Мотогондолы и другие осесимметричные подвески...
Задача: Исследовать характеристики тел вращения
цилиндра, конуса и им подобных.
4.
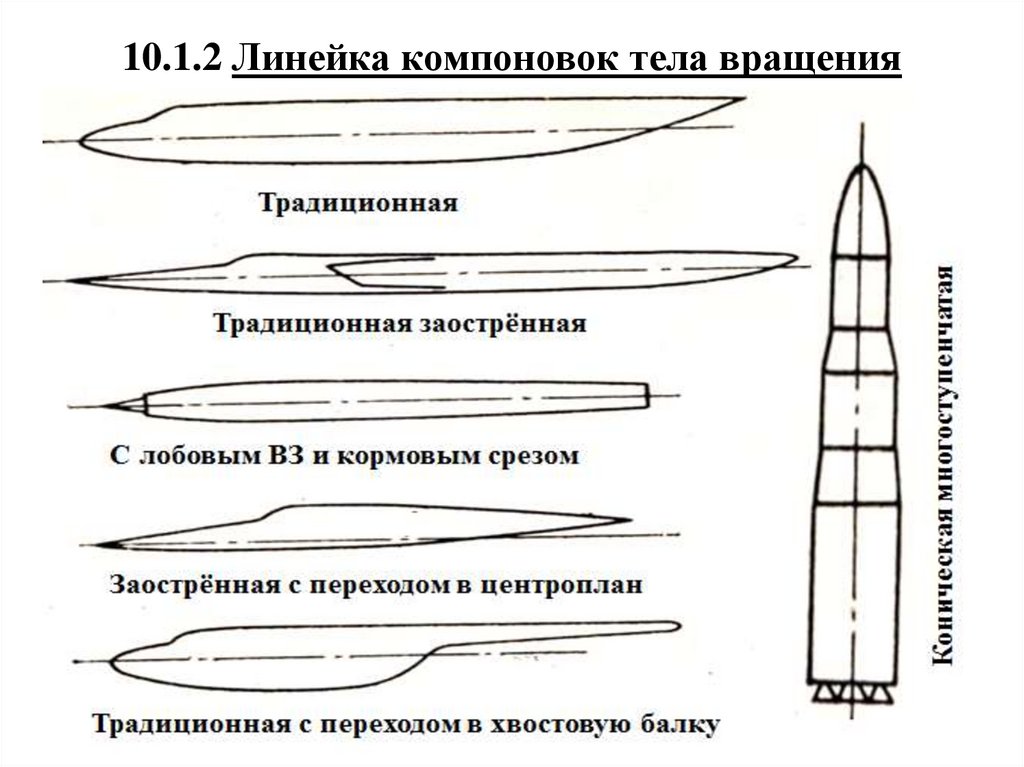
10.1.2 Линейка компоновок тела вращения.
5.
10.1.3 Типовая компоновка тела вращенияСоставные части, их основные геометрические параметры:
головная (lг, dм); цилиндрическая (lц, dм);
кормовая (lц, dм, dк).
Относительные параметры :
удлинение ;
сужение к
lц
λц
;
dм
lк
λк
;
dм
lг
λг
;
dм
l
λ
.
dм
6.
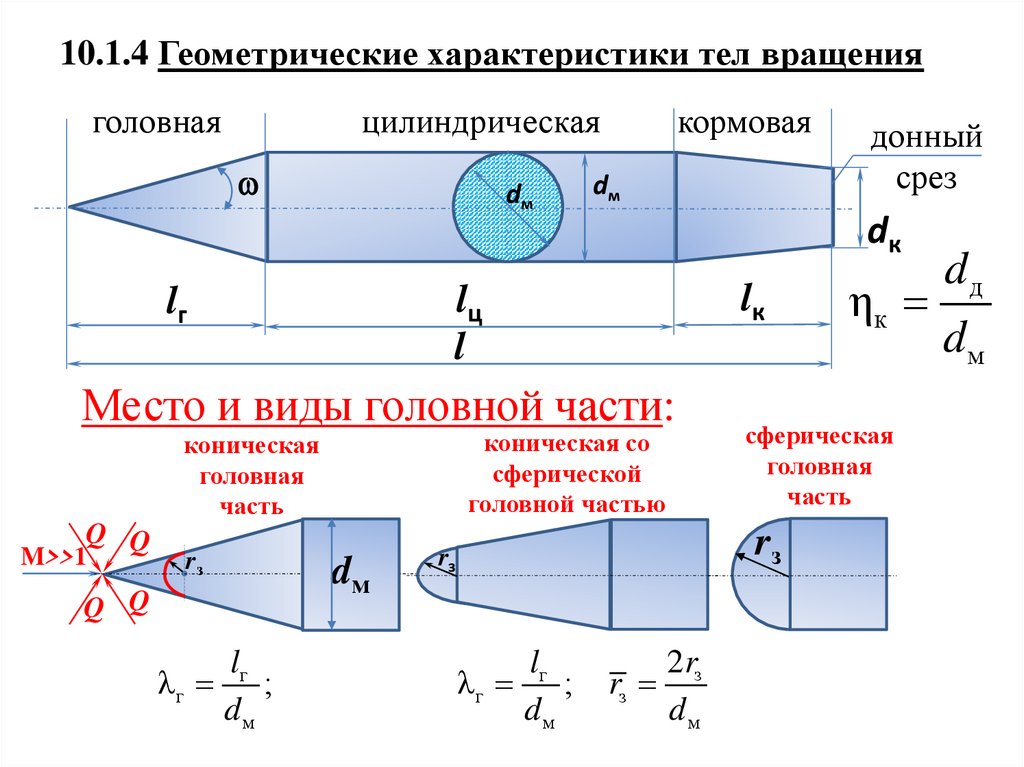
10.1.4 Геометрические характеристики тел вращенияголовная
цилиндрическая
dм
кормовая
dм
dк
lк
lц
l
lг
Место и виды головной части:
коническая со
сферической
головной частью
коническая
головная
часть
Q Q
M>>1
rз
dм
Q Q
λг
lг
;
dм
lг
;
dм
rз
2rз
dм
dд
ηк
dм
сферическая
головная
часть
rз
rз
λг
донный
срез
7.
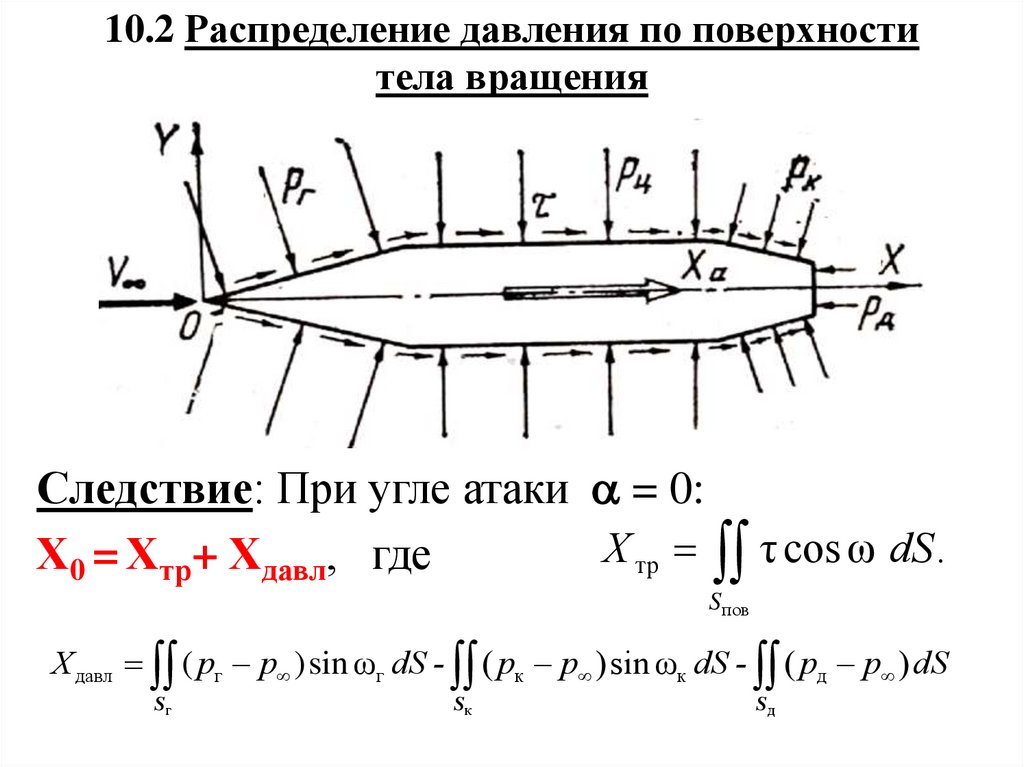
10.2 Распределение давления по поверхноститела вращения
Следствие: При угле атаки = 0:
Х тр τ cos ω dS .
Х0 = Хтр+ Хдавл, где
Sпов
Х давл ( pг p )sin ωг dS - ( pк p )sin ωк dS - ( pд p ) dS
Sг
Sк
Sд
8.
10.3 Аэродинамические характеристики тел вращения. Аэродинамические характеристики определены силами и моментами.
Схема сил тела вращения:
R и M полные аэродинамическая сила и момент соответственно.
X, Y и Z продольная, нормальная и поперечная аэродинамические силы.
Xа , Yа и Zа сила лобового сопротивления, подъёмная и поперечная
аэродинамические силы.
9.
10.3.1 Коэффициенты аэродинамических силМатематическая запись коэффициентов сил X, Y и Z:
ρ V 2
X
Y
Z
сx
; сy
; сz
, где q
p M 2 .
q Sм
q Sм
q Sм
2
2
Математическая запись коэффициентов сил Xа, Yа и Zа:
Xа
Yа
Zа
сx а
; сy а
; сz а
.
q Sм
q Sм
q Sм
Mz
mz
0.
q Sмl
Определения коэффициентов сил и моментов
заложены в формулах:
Коэффициентом подъёмной силы су называется
отношение подъёмной силы Y к скоростному напору q и
Y
площади миделя Sм.
сy
.
q Sм
Далее по образу и подобию.....
10.
10.3.2 Аэродинамические характеристики телвращения
Головная часть (конус). Определение
Аэродинамической характеристикой головной части
называются зависимости коэффициента давления ср0
от числа Маха при постоянны геометрических
параметрах и угле атаки 0.
Анализ: С ростом числа
Маха возрастает величина
скорости V и избыточного
давления по фронтальной
части конуса.
Следовательно, растёт и
коэффициент давления ср.
11.
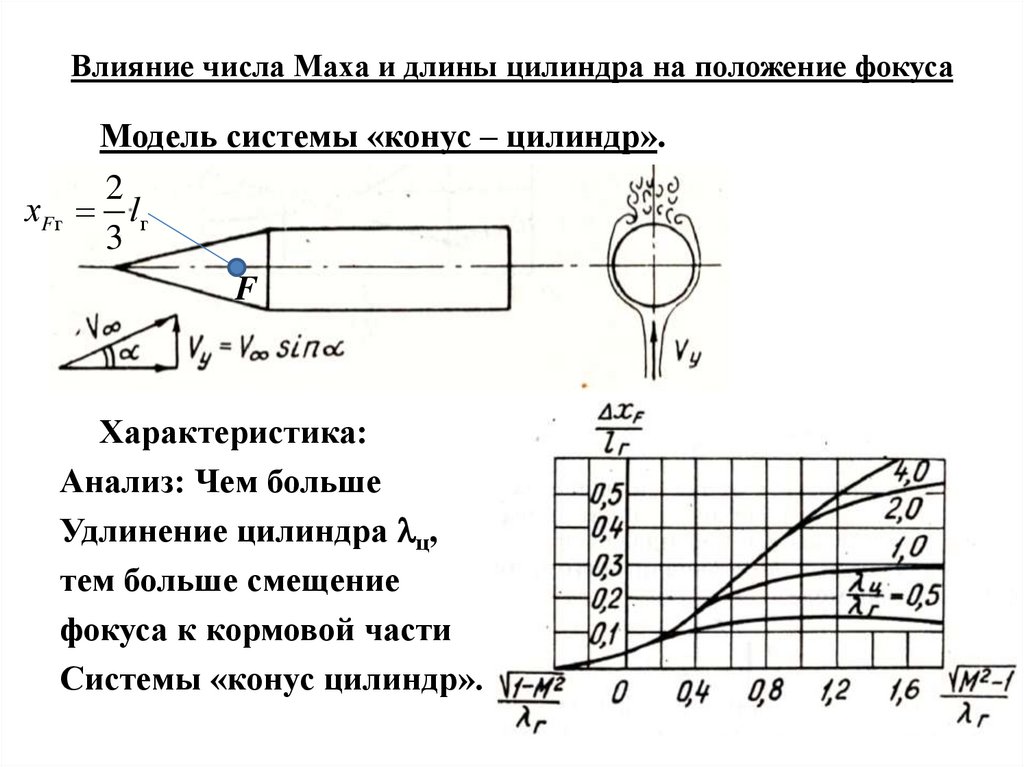
Влияние числа Маха и длины цилиндра на положение фокусаМодель системы «конус – цилиндр».
2
хFг lг
3
F
Характеристика:
Анализ: Чем больше
Удлинение цилиндра ц,
тем больше смещение
фокуса к кормовой части
Системы «конус цилиндр».
12.
Влияние формы корпуса и М на его характеристикиРассмотрим коэффициент лобового сопротивления:
сх0 = сх тр + сх в0 +сх.д.
Имеем:
Сх д
Сх в 0
влияние удлинения на сх0;
Сх тр
влияние числа М на сх0.
Анализ по компонентам: САМОСТОЯТЕЛЬНО!
13.
Влияние числа Маха на аэродинамическиехарактеристики корпуса
Подобно крылу влияние числа Маха
определено волновым сопротивлением как на
дозвуке, трансзвуке, так и на больших М .
14.
10.4 Донное сопротивление10.4/1 Донное сопротивление при М<1
Донное сопротивление сопротивление сил давления, приложенное к
донному срезу тела вращения со стороны разрежения, создаваемого
аэродинамической тенью за донным срезом и отсосом донной среды
путём её эжекции.
Примечание: Полагают, донное сопротивление – разрежение за донным срезом корпуса.
Рабочий процесс ДC при М<1 динамический
отрыв потока на задней кромке кормы тела с
последующим формированием цепочки
кольцевых вихрей и зоны низкого давления рд,
создающего силу донного давления Хд:
X д ( pд p ) dS.
Sд
Эжекция во внешний поток частично снижает донное давление рд. Она
определена формой кормовой части, числами M и Re, толщиной и структурой
пограничного слоя. Математически, в поле такого влияния коэффициент сх.д:
3
S
0, 029 d д
0, 029 d д
с х д = с р д д , где с р д
. Тогда с х . д =
.
Sм
сх.тр d м
сх.тр d м
Для корпусов большого удлинения характерно: рд const.
15.
10.4.1 Коэффициент донного сопротивления при М > MкрПри транс- и сверхзвуковых скоростях рабочий процесс потока
у донного среза усложняется. Сверхзвуковой поток, проходя пучок
характеристик (волн разрежения), разгоняется, донное давление
снижается (см. УБ), а его сила Хрд значительно возрастают.
За донным срезом сверхзвуковой поток затормаживается на
скачке уплотнения и становится дозвуковым. Статическое
давление скачкообразно возрастает. Но в силу удаления скачка от
донного среза давление рд на её поверхности и коэффициент сх д
изменяются незначительно.
16.
Подъёмная сила корпусаПодъёмная сила корпуса Ya проекция полной
аэродинамической силы R на направление, перпендикулярное
скорости V набегающего потока .
Рабочий процесс: Подъёмная сила корпуса следствие
приложения разности давления (рн-рв), к нижней и верхней его
поверхностям на углах 0. По теории тонкого тела Yц = 0.
Тогда несущие свойства корпуса определены производными
головной (г) и кормовой (к) частей. А именно:
y a.г
с
2,0.
y a.к
с
Sд
2 1 .
Sм
α
ya
с =с
α
y a .г
+с
α
y a.к
Sд
=2 .
Sм
17.
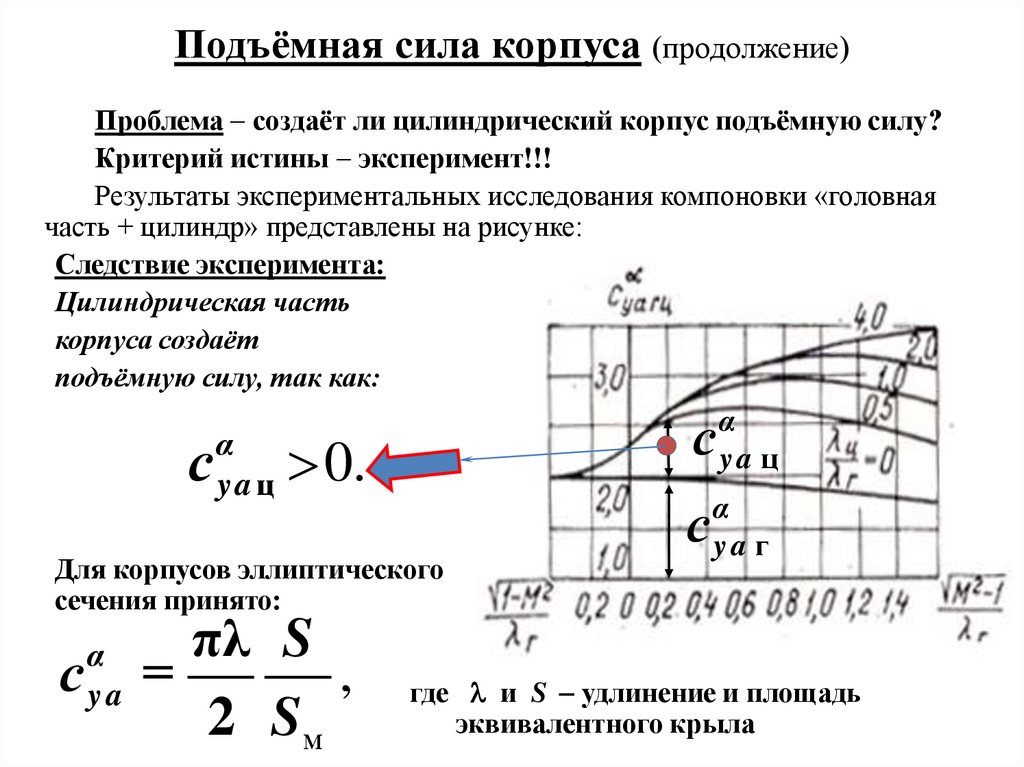
Подъёмная сила корпуса (продолжение)Проблема создаёт ли цилиндрический корпус подъёмную силу?
Критерий истины эксперимент!!!
Результаты экспериментальных исследования компоновки «головная
часть + цилиндр» представлены на рисунке:
Следствие эксперимента:
Цилиндрическая часть
корпуса создаёт
подъёмную силу, так как:
с
α
yaц
с
0.
Для корпусов эллиптического
сечения принято:
с
α
ya
πλ S
=
,
2 Sм
с
α
ya ц
α
ya г
где и S удлинение и площадь
эквивалентного крыла
18.
Индуктивное сопротивление корпусаПодсасывающая сила корпуса отсутствует. Тогда
коэффициент индуктивного сопротивления определён:
сх а = сх 0 + сyа = f(сyа, ).
Аэродинамический
фокус
точка
пересечения
равнодействующей всех аэродинамических сил (R) с осью
симметрии корпуса.
Координата фокуса отсчитывается от носка корпуса до точки
пересечения равнодействующей всех аэродинамических сил (R) с
осью симметрии корпуса. Она выражается через производные
подъёмных сил составных частей корпуса.
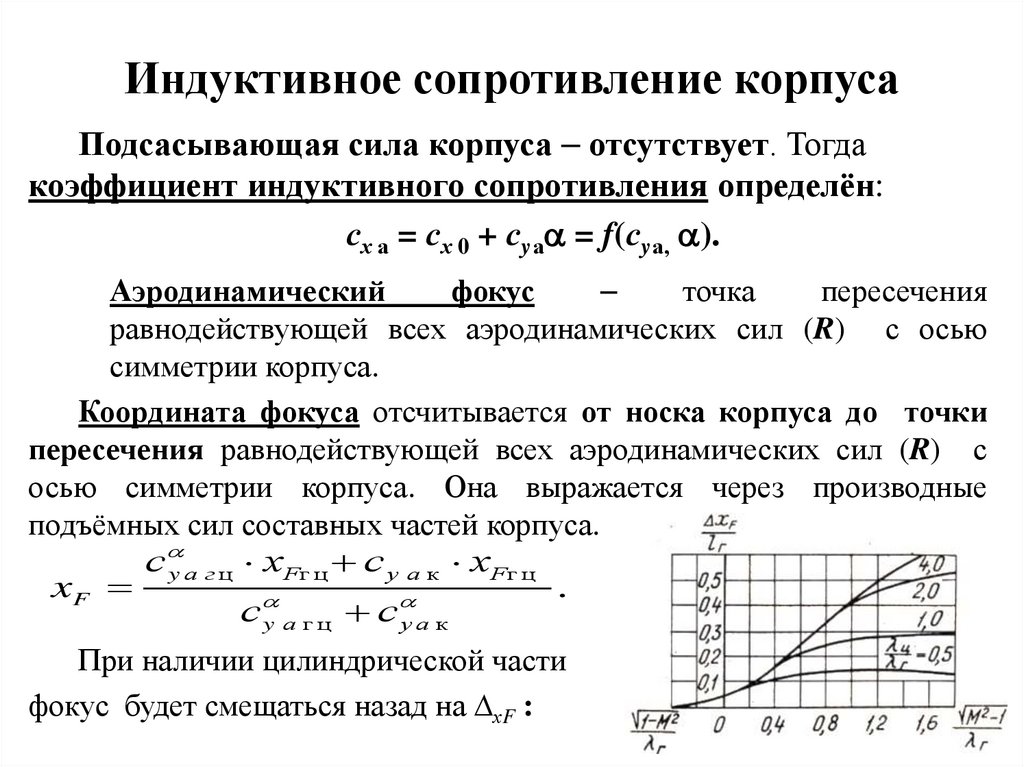
с y а г ц xFг ц с y а к xFг ц
xF
.
сy а г ц сy а к
При наличии цилиндрической части
фокус будет смещаться назад на хF :












 industry
industry








