Similar presentations:
Счетчики импульсов с принудительным насчетом. Принудительный насчет
1.
Счетчики импульсов с принудительным насчетомРассматриваемые недвоичные счетчики обладают некоторыми особенностями: исключение
ряда возможных комбинаций осуществляется принудительно, т.е. триггеры счетчика за
счет обратных связей и системных решений принудительно устанавливаются в
определенное состояние. При этом следующий цикл счета может начинаться как с
нулевого исходного состояния счетчика, так и с произвольного начального кода.
Рассмотрим пример построения счетчика с принудительным насчетом, в котором
отдельные его состояния исключаются, а все триггеры счетчика принудительно
устанавливаются в состояние 1.
Работа счетчика с принудительным насчетом: начиная с нулевого исходного состояния, с
каждым очередным импульсом состояния счетчика изменяются в естественном порядке до
определенного (n-го) набора. Следующий счетный импульс устанавливает счетчик не в п+1
состояние, а в последнее 2N-1
состояние (N-число триггеров счетчика). Таким образом, некоторые состояния счетчика
исключаются (они пропускаются) и KC4^2N. Очередным импульсом счетчик возвращается в
исходное нулевое состояние и далее начинается аналогичный цикл счета.
2.
Принудительный насчет достигается введением обратных связей с выходов триггеров наустановочные входы тех триггеров, которые на n-ом наборе были в состоянии Qj=() и
очередным импульсом принудительно должны переключиться в состояние 1.
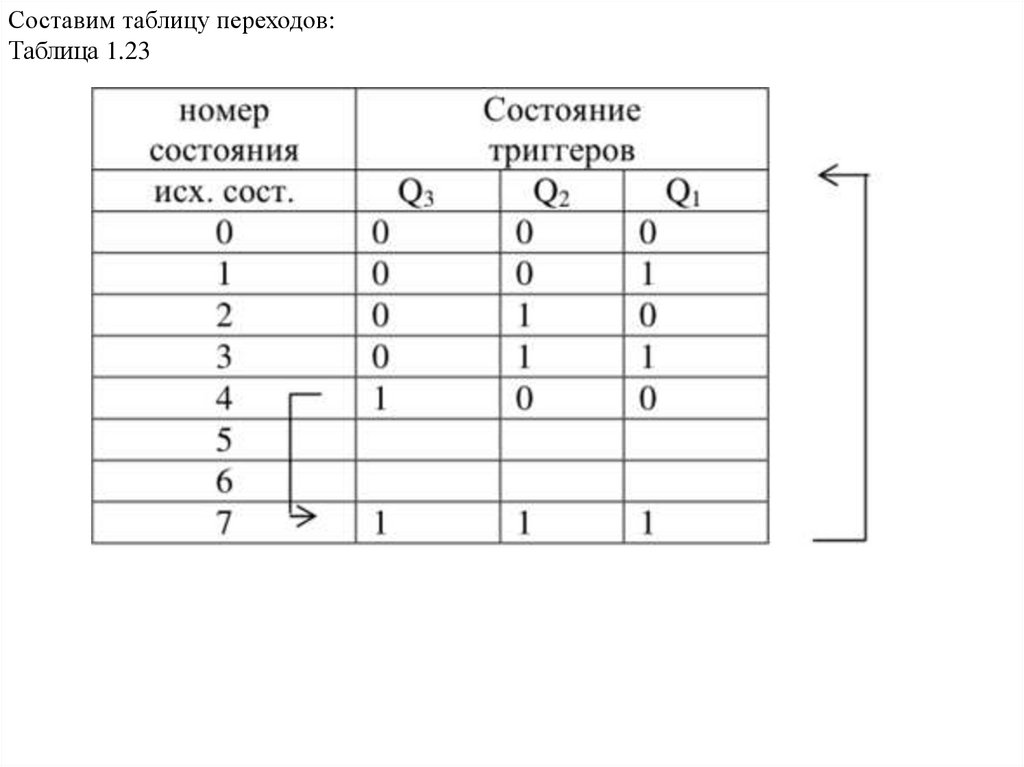
Рассмотрим работу счетчика с принудительным насчетом с Ксч=6.
Для реализации такого счетчика необходимо 3 триггера (КСЧ=2Х=8), при этом исключаются
2 любых состояния (для определенности исключим 5 и 6).
3.
Составим таблицу переходов:Таблица 1.23
4.
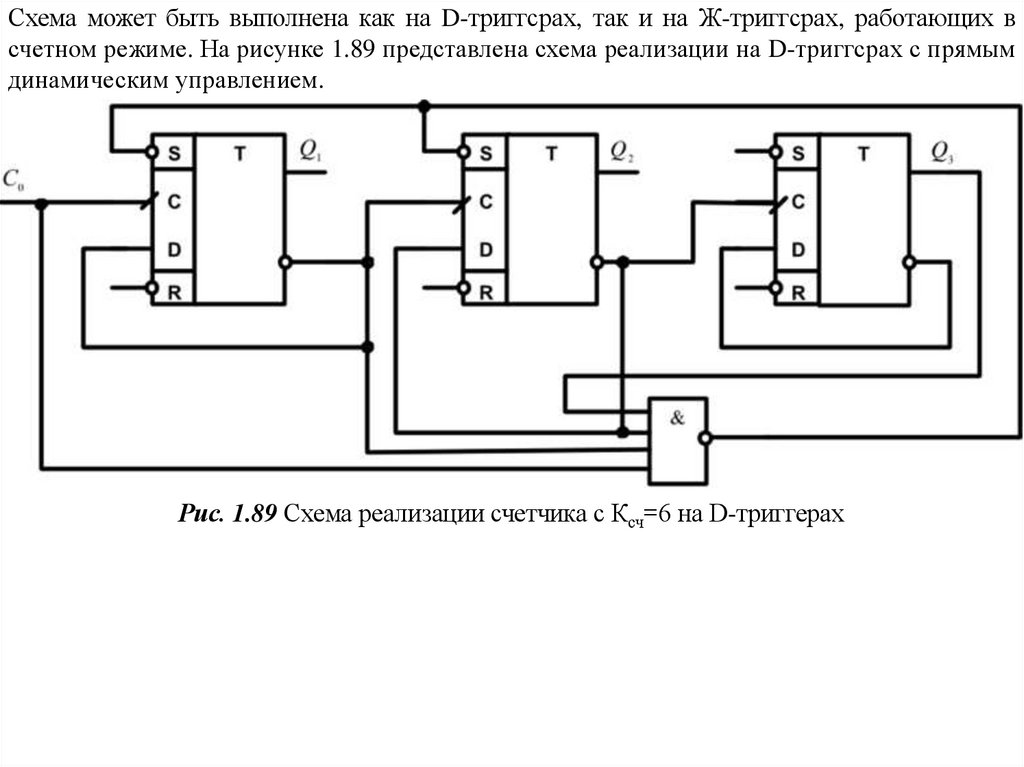
Схема может быть выполнена как на D-триггсрах, так и на Ж-триггсрах, работающих всчетном режиме. На рисунке 1.89 представлена схема реализации на D-триггсрах с прямым
динамическим управлением.
Рис. 1.89 Схема реализации счетчика с Ксч=6 на D-триггерах
5.
Для исключения двух состояний счетчика вводится обратная связь через ЛЭ И-НЕ наинверсные установочные входы S триггеров Т] и Т2 (либо через ЛЭ И на прямые
установочные входы S).
До состояния 100 счетчик работает как обычный суммирующий счетчик с
последовательным переносом. С поступлением 4-го счетного импульса устанавливается
состояние:
6.
Логический элемент И-НЕ подготовлен к работе, т.к. на его трех входах 1. С очередным(пятым) импульсом на выходе ЛЭ И-НЕ формируется 0, который подается на инверсные
установочные входы триггеров Т, и Т2, переводя их в состояние <2, = (9, = 1 (состояние
триггера Т3 не изменяется: (9, = 1).
Таким образом, состояния счетчика 5 и 6 пропускаются, т.е. происходит принудительный
насчет (пропуск) двух состояний счетчика и Ксч=2х-2=6.
Новый цикл счета осуществляется в том же естественном порядке, начиная с исходного
нулевого состояния. Переход в него из состояния 111 происходит как в обычном
суммирующем счетчике с последовательным переносом.
В ряде случаев для формирования сигнала принудительного насчста используется
асинхронный RS-триггер, что позволяет повысить надежность работы счетчика.
Изменяя коммутацию, можно получить любой коэффициент счета в пределах
возможностей счетчика, т.е. количества включенных триггеров, определяющих число
состояния счетчика.
7.
Счетчики импульсов с начальной установкой кодаЭтот вид счетчиков в общем случае можно отнести к счетчикам с принудительным
насчстом, у которых насчет осуществляется нс в процессе счета, а посредством установки
счетчика в исходное состояние, соответствующее числу пропускаемых состояний.
Принцип построения и работу таких счетчиков рассмотрим на примере для Ксч=9. Для
реализации счетчика потребуется 4 триггера (Ксч>9). Исключению подлежат первые 2NKC4= 16-9=7 комбинаций.
Таким образом исходное состояние счетчика должно соответствовать коду 0111 (а нс 0000
как было в ранее рассмотренном счетчике). Установка исходного состояния в процессе
счета проводится сигналами с выходов триггеров через схему управления на ЛЭ И Н-4
(первоначальная - по шине «Уст.»).
8.
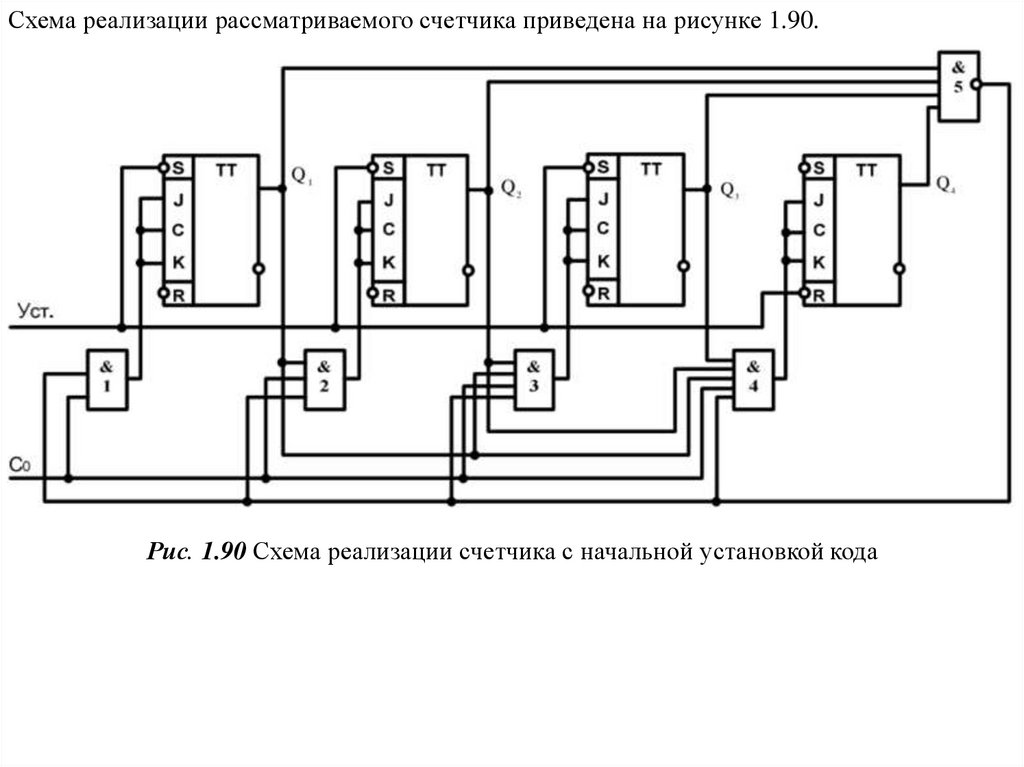
Схема реализации рассматриваемого счетчика приведена на рисунке 1.90.Рис. 1.90 Схема реализации счетчика с начальной установкой кода
9.
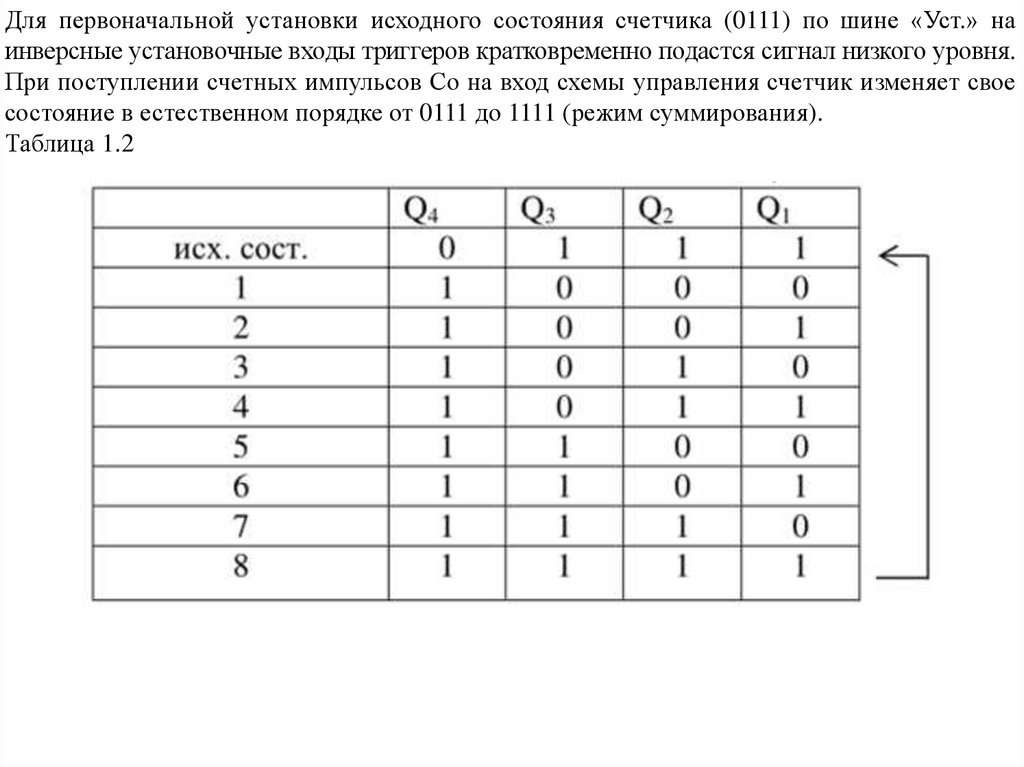
Для первоначальной установки исходного состояния счетчика (0111) по шине «Уст.» наинверсные установочные входы триггеров кратковременно подастся сигнал низкого уровня.
При поступлении счетных импульсов Со на вход схемы управления счетчик изменяет свое
состояние в естественном порядке от 0111 до 1111 (режим суммирования).
Таблица 1.2
10.
ЛЭ И-НЕ №5 при этом не оказывает влияния на работу счетчика, т.к. в любом из наборов(до 7 включительно) в одном из разрядов Q присутствует 0 и, следовательно, на выходе ЛЭ
№5 всегда формируется 1, подаваемая на ЛЭ И №1-3.
Восьмым счетным импульсом в счетчике устанавливается комбинация 1111
(<2, = <2, = Qy — <24 = 1) и на выходе ЛЭ И-НЕ №5 формируется 0, который блокирует 1,2
и 3 ЛЭ И (т.е. состояние 1 -3 триггеров нс изменится очередным импульсом).
Очередной 9-й импульс через ЛЭ И №4 поступает на счетный вход триггера старшего
(четвертого) разряда, изменяя его состояние на противоположное и устанавливая в итоге
начальный код 0111. Очередной цикл счета выполняется аналогично.
Изменяя коммутацию, можно реализовать любой коэффициент счета в пределах
возможностей счетчика, т.е. числа включенных триггеров.
11.
Понятие об адресных счетчикахВ устройствах управления ЭВМ и автоматики часто возникает необходимость задания
начального адреса команды с последующим увеличением номера адреса на 1.
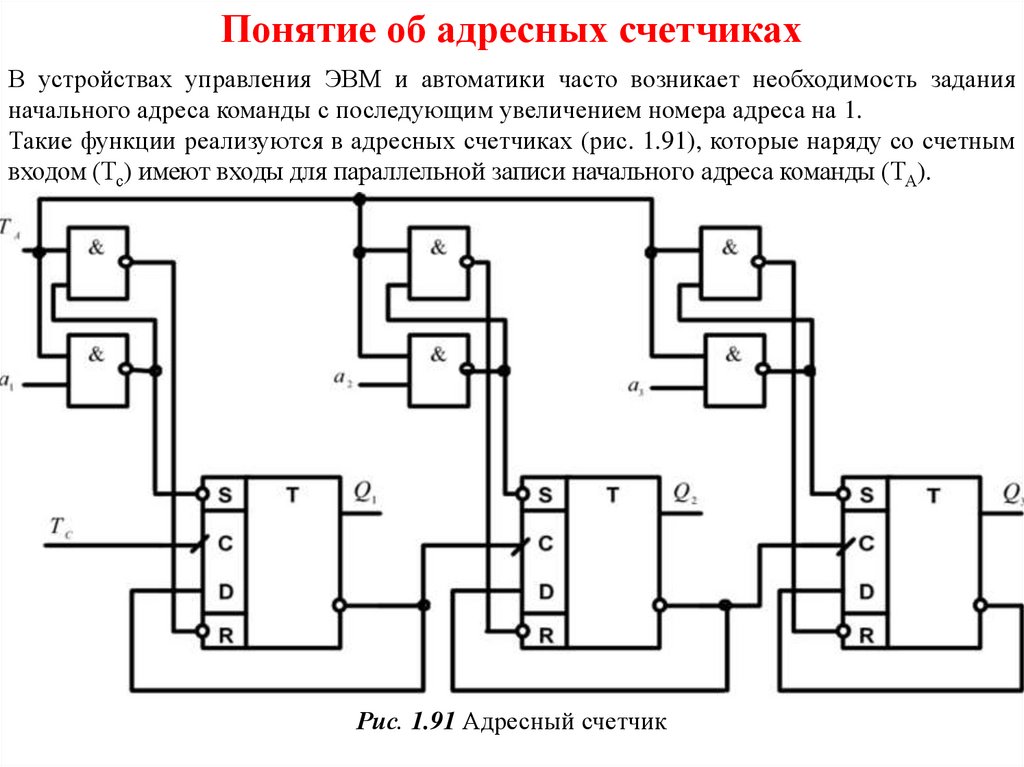
Такие функции реализуются в адресных счетчиках (рис. 1.91), которые наряду со счетным
входом (Тс) имеют входы для параллельной записи начального адреса команды (ТА).
Рис. 1.91 Адресный счетчик
12.
Счетчик выполнен на D-триггерах с динамическим управлением, работающих в счетном режиме. Спомощью установочных входов S и R осуществляется запись начального адреса. Так, если требуется
начать счет с адреса 101 (А|=1, А2=0, А3=1), то после подачи импульса ТА в счетчике установится
состояние: Qi=l, Q2=(), Q3=l (в момент записи адреса счетные импульсы на входе Тс должны
отсутствовать).
Таким образом, в данном примере счет начинается с кода 101, продолжается в обычном
(естественном) порядке до 111. Далее происходит сброс всех триггеров в 0 и начинается новый цикл
счета, как в обычном суммирующем счетчике с последовательным переносом.
Рассмотренные способы построения недвоичных счетчиков позволяют получать любые значения Кеч.
В аппаратуре ЦСПИ счетчики с различными модулями счета находят применение в формирователях
последовательностей продвигающих (тактовых) импульсов от одного опорного генератора, в
устройствах отображения информации (декадные счетчики с Ксч=10) и в др. случаях.
Цифровые счетчики с КСЧ^2Ы реализованы в ряде серий микросхем. Например, десятичные счетчики
К155ИЕ6, К561ИЕ8, К500ИЕ137. Другие типы двоично-десятичных счетчиков можно найти в
справочниках по цифровым микросхемам.
13.
Цифровые счетчики в режиме деления числа ичастоты импульсов
Рассмотренные ранее двоичные и недвоичные счетчики импульсов обеспечивают счет
входных импульсов либо в режиме суммирования (чаще), либо в режиме вычитания. При
этом триггеры более старших разрядов счетчика изменяют свое состояние реже по
сравнению с триггерами младших разрядов, т.е. период следования импульсов на выходе
триггера старшего разряда оказывается больше периода входных импульсов в Кеч раз. По
этой причине любой из этих счетчиков можно рассматривать как счстчик-делитель частоты
входных импульсов.
Отношение Твых/Твх в данном случае равное Кеч называют коэффициентом деления
частоты:
Ксч=Т вых/Т вх=Евх/Евых=Кдел.
Использование ЦСИ для деления частоты находит широкое применение в генераторах
тактовой частоты, в синтезаторах частоты радиопередатчиков и приемников, устройствах
контроля, бытовой технике и т.п.
14.
Для деления числа импульсов в схему счетчика-делителя вводится дополнительная схемаформирования
выходных
импульсов,
позволяющая
получить
выходную
последовательность импульсов с параметрами:
Твых=КделТвх и Швых=1ивхТакая схема может быть использована как распределитель сигналов с одного входа на
несколько выходов.
В данной лекции рассматриваются счетчики-делители, в работе которых применены
другие принципы, связанные с продвижением счетных импульсов. При этом можно
получить как четные, так и нечетные коэффициенты деления, как кратные, так и не
кратные 2N. В таких счетчиках информация передается только между двумя соседними
триггерами, что обеспечивает повышение быстродействия счетчика.
15.
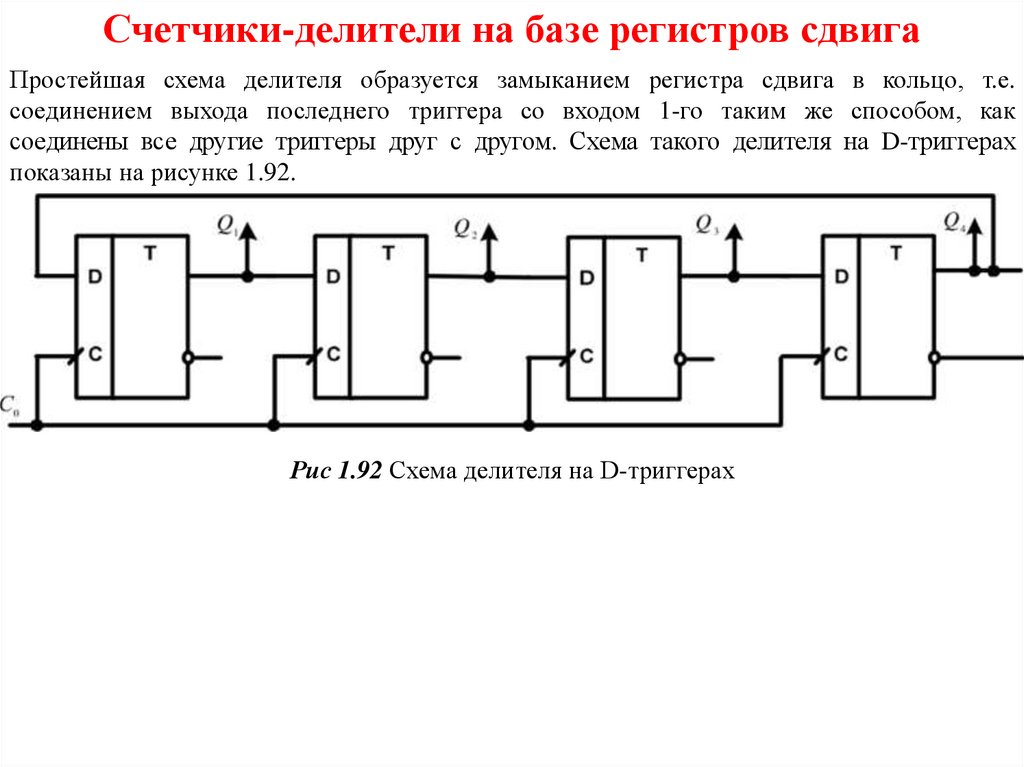
Счетчики-делители на базе регистров сдвигаПростейшая схема делителя образуется замыканием регистра сдвига в кольцо, т.е.
соединением выхода последнего триггера со входом 1-го таким же способом, как
соединены все другие триггеры друг с другом. Схема такого делителя на D-триггерах
показаны на рисунке 1.92.
Рис 1.92 Схема делителя на D-триггерах
16.
Особенностью такого делителя, по сравнению с обычным счетчиком является то, что здесьКдел=Ы и, следовательно, для одинаковых значений Кдел требуется большее число
триггеров. Но данный способ деления обладает существенным достоинством - высоким
быстродействием. Это можно объяснить тем, что в этой схеме происходит не счет
импульсов, связанный с распространением переноса, а сдвиг записанной информации, при
котором сигнал передается всегда только между соседними триггерами.
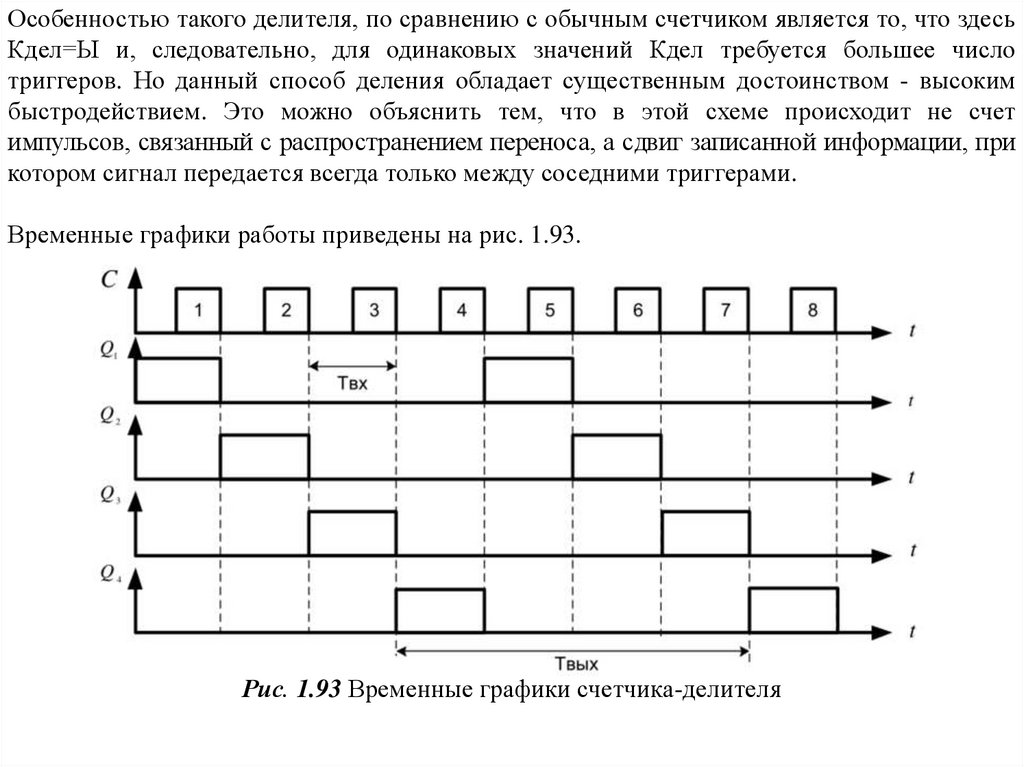
Временные графики работы приведены на рис. 1.93.
Рис. 1.93 Временные графики счетчика-делителя
17.
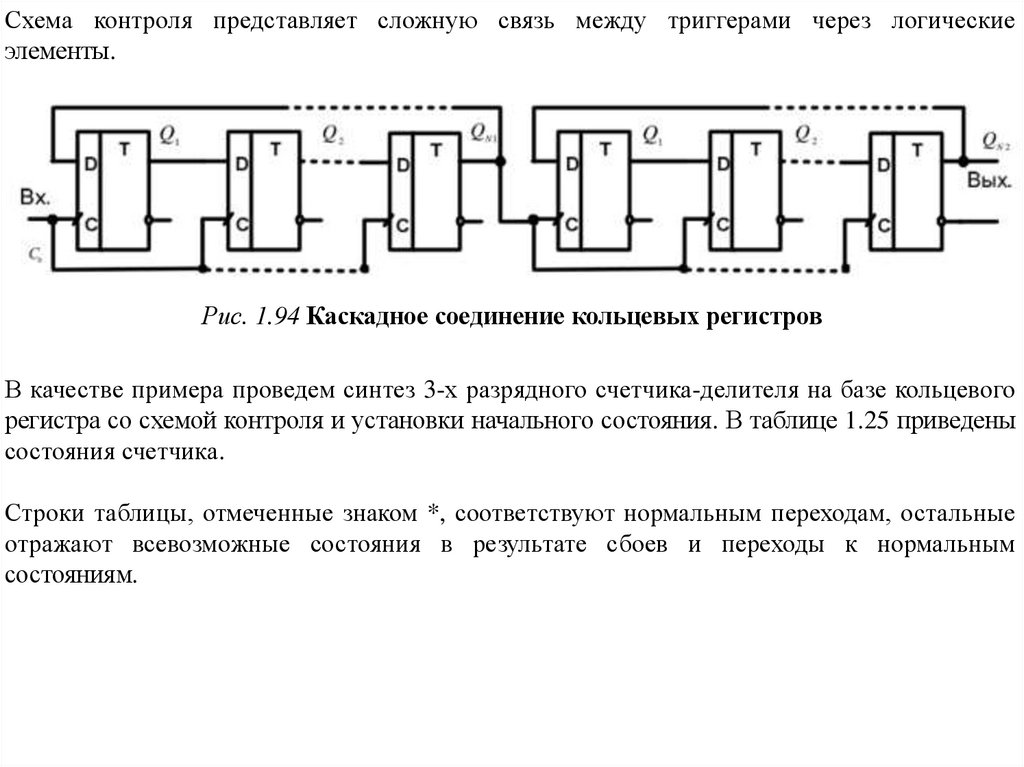
При построении делителей с большим Кдел с целью уменьшения числа триггеровприменяют каскадное соединение кольцевых регистров с меньшим Кеч (рис. 1.94). При
этом перед началом работы в один из триггеров каждого кольцевого регистра необходимо
записать 1.
Выходные импульсы первого N1-разрядного регистра служат сдвигающими импульсами
для второго N2- разрядного регистра. В результате Kne4=N!N2.
Для обеспечения надежной работы делителя он нуждается в дополнительной схеме
контроля и записи начального состояния. Это объясняется тем, что в таком делителе в
случае сбоя, в результате которого все триггеры перейдут в состояние 0 или несколько
триггеров (а не один) перейдут в состояние 1, нормальная работа делителя прекращается
на неопределенное время. В первом случае на выходе ничего не будет, во втором - Кеч
уменьшится.
18.
Схема контроля представляет сложную связь между триггерами через логическиеэлементы.
Рис. 1.94 Каскадное соединение кольцевых регистров
В качестве примера проведем синтез 3-х разрядного счетчика-делителя на базе кольцевого
регистра со схемой контроля и установки начального состояния. В таблице 1.25 приведены
состояния счетчика.
Строки таблицы, отмеченные знаком *, соответствуют нормальным переходам, остальные
отражают всевозможные состояния в результате сбоев и переходы к нормальным
состояниям.
19.
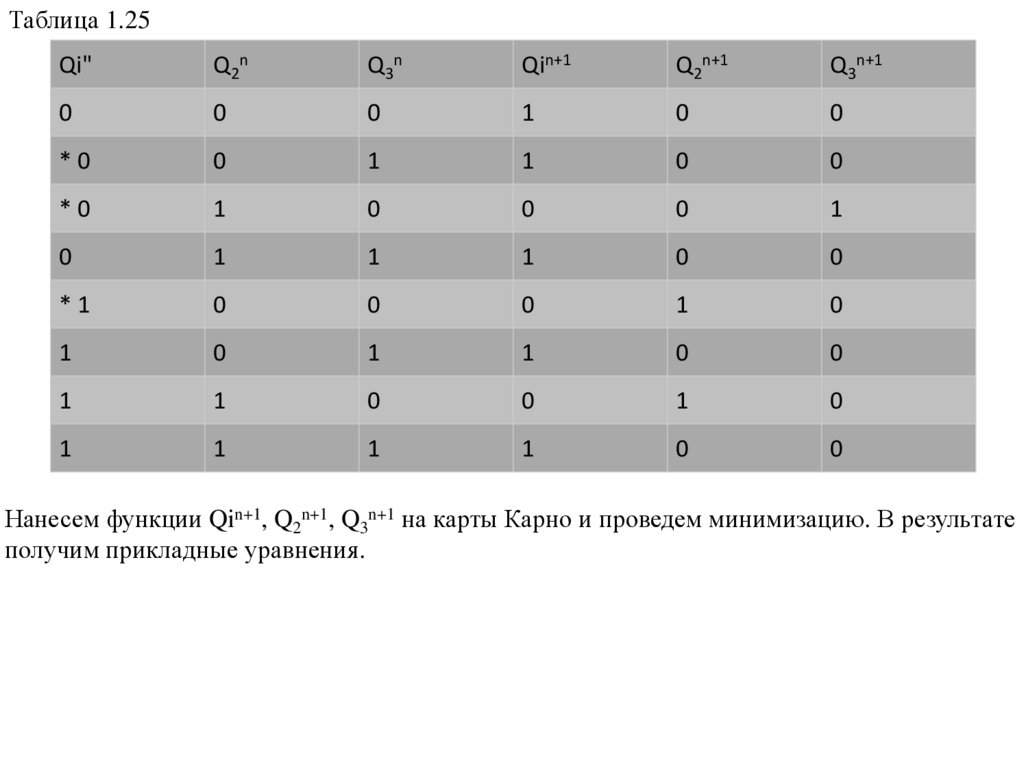
Таблица 1.25Qi"
Q2 n
Q3 n
Qin+1
Q2n+1
Q3n+1
0
0
0
1
0
0
*0
0
1
1
0
0
*0
1
0
0
0
1
0
1
1
1
0
0
*1
0
0
0
1
0
1
0
1
1
0
0
1
1
0
0
1
0
1
1
1
1
0
0
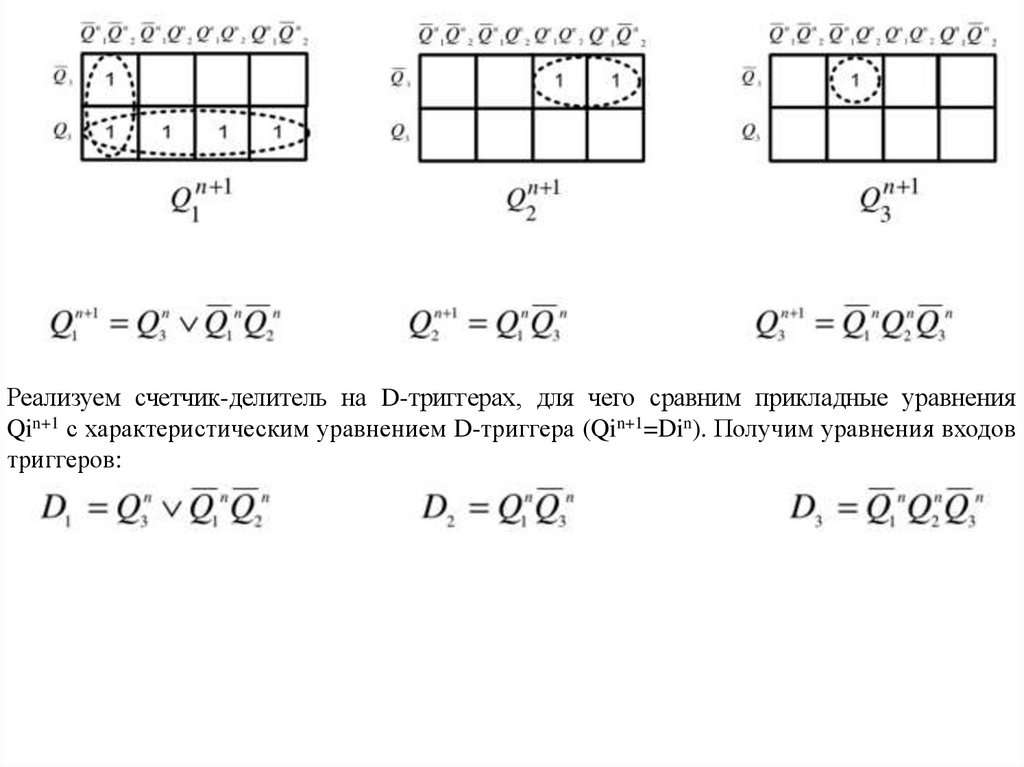
Нанесем функции Qin+1, Q2n+1, Q3n+1 на карты Карно и проведем минимизацию. В результате
получим прикладные уравнения.
20.
Реализуем счетчик-делитель на D-триггерах, для чего сравним прикладные уравненияQin+1 с характеристическим уравнением D-триггера (Qin+1=Din). Получим уравнения входов
триггеров:
21.
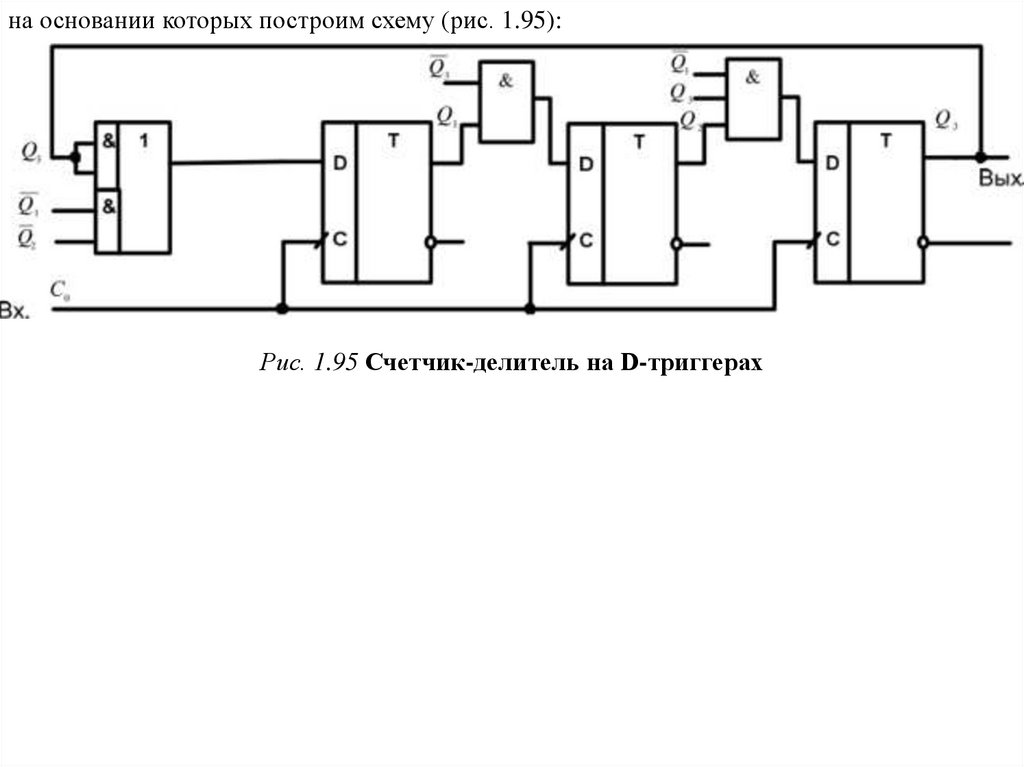
на основании которых построим схему (рис. 1.95):Рис. 1.95 Счетчик-делитель на D-триггерах
22.
В таком счетчике в случае сбоя очередным входным импульсом устанавливается одно изсостояний, при котором 1 записывается только в одном разряде. Далее продолжается
нормальная работа. Не трудно убедиться, что начальное состояние счетчика
устанавливается автоматически первым входным импульсом.
Пример: пусть в результате сбоя установилось состояние регистра: Qi=0, Q2=l, Q3=l- Тогда
на входах D-триггеров имеем:
Следовательно, при поступлении очередного входного импульса счетчик перейдет в
состояние Qi=l, Q2=0, Q3=0, т.е. восстановится нормальная работа.
23.
Счетчики-делители с переменным модулем счетаВ ряде случаев возникает необходимость построения счетчиков- делителей с переменным
(заданным) коэффициентом деления.
Синтез подобных счетчиков выполняется в следующей последовательности:
- по заданной логике работы (смене комбинаций) счетчика составляется таблица
переходов. При этом факультативные условия используются либо на неиспользованных
наборах, либо с заданными ограничениями;
- для Q"+l составляются карты Карно и выполняется минимизация с учетом ФУ. В
результате получаем прикладные уравнения для Q"+l;
- выбирается база для реализации счетчика (триггеры JK- или D-типов). Совместно
решаются соответствующие характеристические и прикладные уравнения, что дает
уравнения входов триггеров;
- строится схема реализации, включающая триггеры и, при необходимости, логическую
схему;
- проверяется логика работы, приводятся соответствующие временные графики.
24.
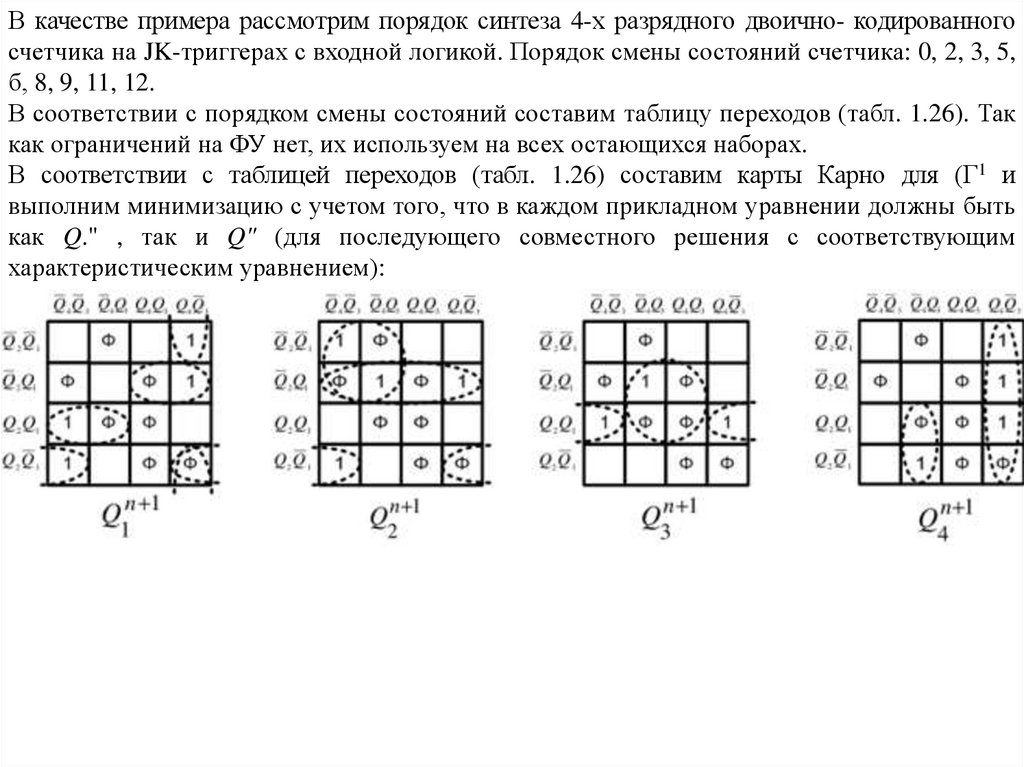
В качестве примера рассмотрим порядок синтеза 4-х разрядного двоично- кодированногосчетчика на JK-триггерах с входной логикой. Порядок смены состояний счетчика: 0, 2, 3, 5,
б, 8, 9, 11, 12.
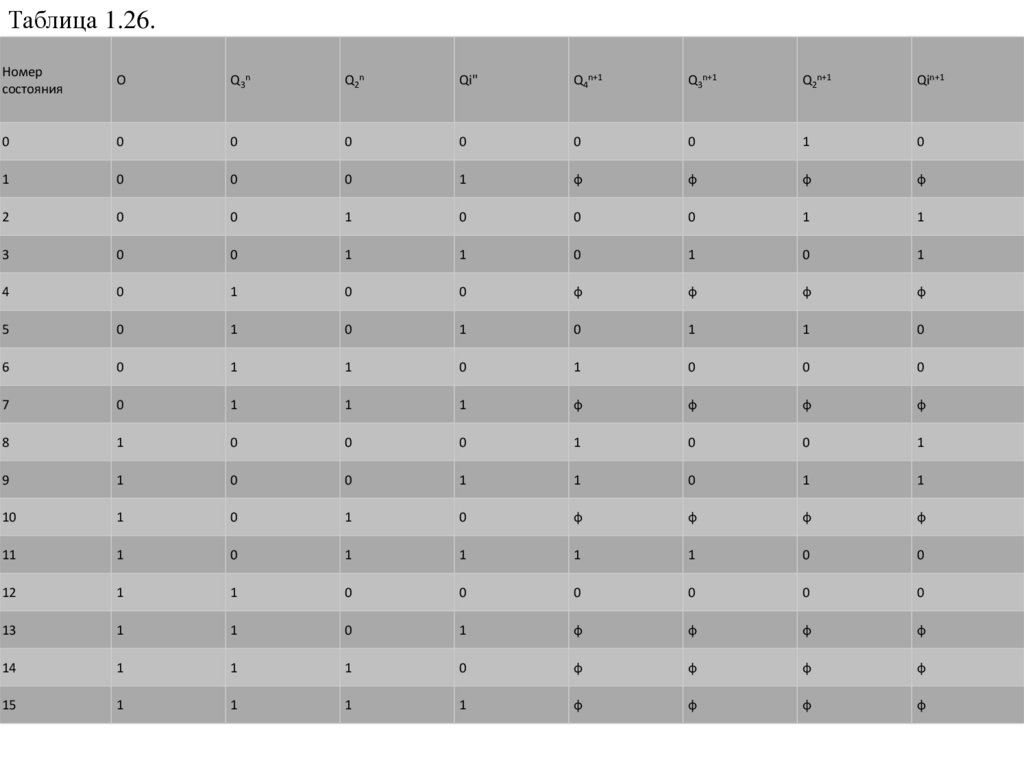
В соответствии с порядком смены состояний составим таблицу переходов (табл. 1.26). Так
как ограничений на ФУ нет, их используем на всех остающихся наборах.
В соответствии с таблицей переходов (табл. 1.26) составим карты Карно для (Г1 и
выполним минимизацию с учетом того, что в каждом прикладном уравнении должны быть
как Q." , так и Q" (для последующего совместного решения с соответствующим
характеристическим уравнением):
25.
Таблица 1.26.Номер
состояния
О
Q3n
Q2n
Qi"
Q4n+1
Q3n+1
Q2n+1
Qin+1
0
0
0
0
0
0
0
1
0
1
0
0
0
1
ф
ф
ф
ф
2
0
0
1
0
0
0
1
1
3
0
0
1
1
0
1
0
1
4
0
1
0
0
ф
ф
ф
ф
5
0
1
0
1
0
1
1
0
6
0
1
1
0
1
0
0
0
7
0
1
1
1
ф
ф
ф
ф
8
1
0
0
0
1
0
0
1
9
1
0
0
1
1
0
1
1
10
1
0
1
0
ф
ф
ф
ф
11
1
0
1
1
1
1
0
0
12
1
1
0
0
0
0
0
0
13
1
1
0
1
ф
ф
ф
ф
14
1
1
1
0
ф
ф
ф
ф
15
1
1
1
1
ф
ф
ф
ф
26.
Прикладные уравнения имеют вид:При реализации счетчика на JK-триггерах, характеристическое уравнение которого
получим следующие уравнения входов:
27.
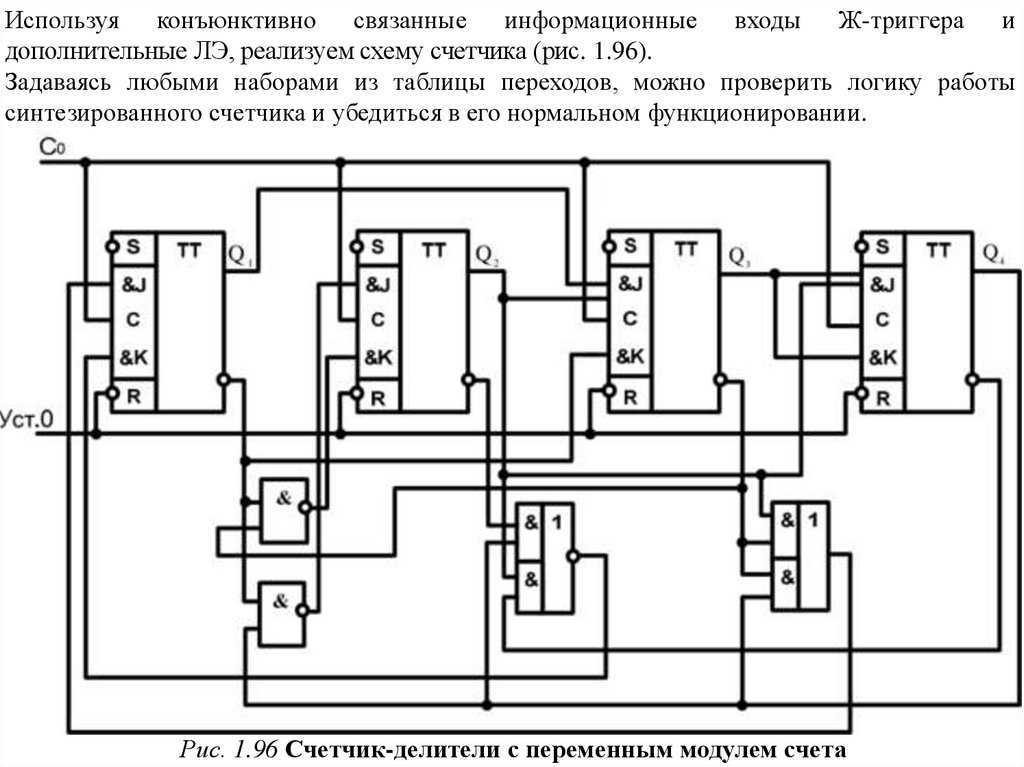
Используя конъюнктивно связанные информационные входы Ж-триггера идополнительные ЛЭ, реализуем схему счетчика (рис. 1.96).
Задаваясь любыми наборами из таблицы переходов, можно проверить логику работы
синтезированного счетчика и убедиться в его нормальном функционировании.
Рис. 1.96 Счетчик-делители с переменным модулем счета
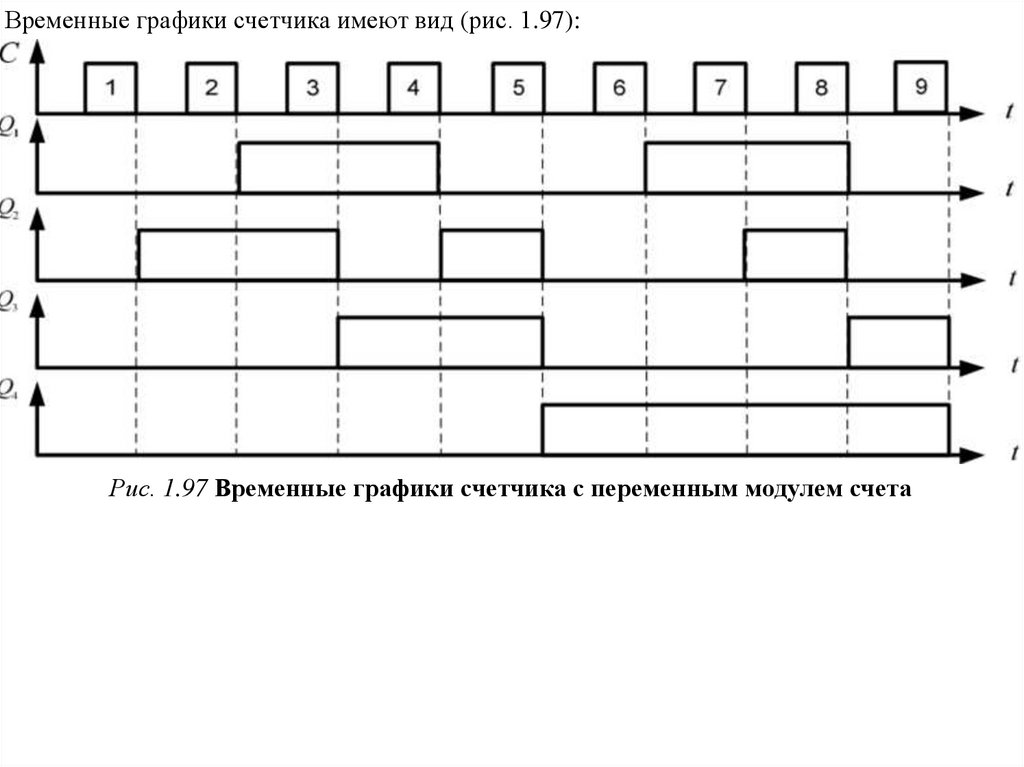
28.
Временные графики счетчика имеют вид (рис. 1.97):Рис. 1.97 Временные графики счетчика с переменным модулем счета
29.
Счетчики-делители на базе регистров сдвига сперекрестными связями
Для получения четных и нечетных коэффициентов деления широко применяются
счетчики-делители на базе регистров сдвига с перекрестными связями:
а) счетчик-делитель с четным коэффициентом деления (Kc4=2N)
В таких счетчиках все связи между триггерами обычные, за исключением одной связи
между последним и первым триггерами, которая делается перекрестной и обеспечивает
инверсную перезапись информации из последнего триггера в первый.
В счетчиках на JK-триггерах или RS-триггерах прямой выход последнего триггера
соединяют с входом К (или R) первого, а инверсный выход последнего - с входом J (или S)
первого триггера. Если счетчик реализован на D-триггерах, то с входом D первого триггера
соединяется инверсный выход последнего.
30.
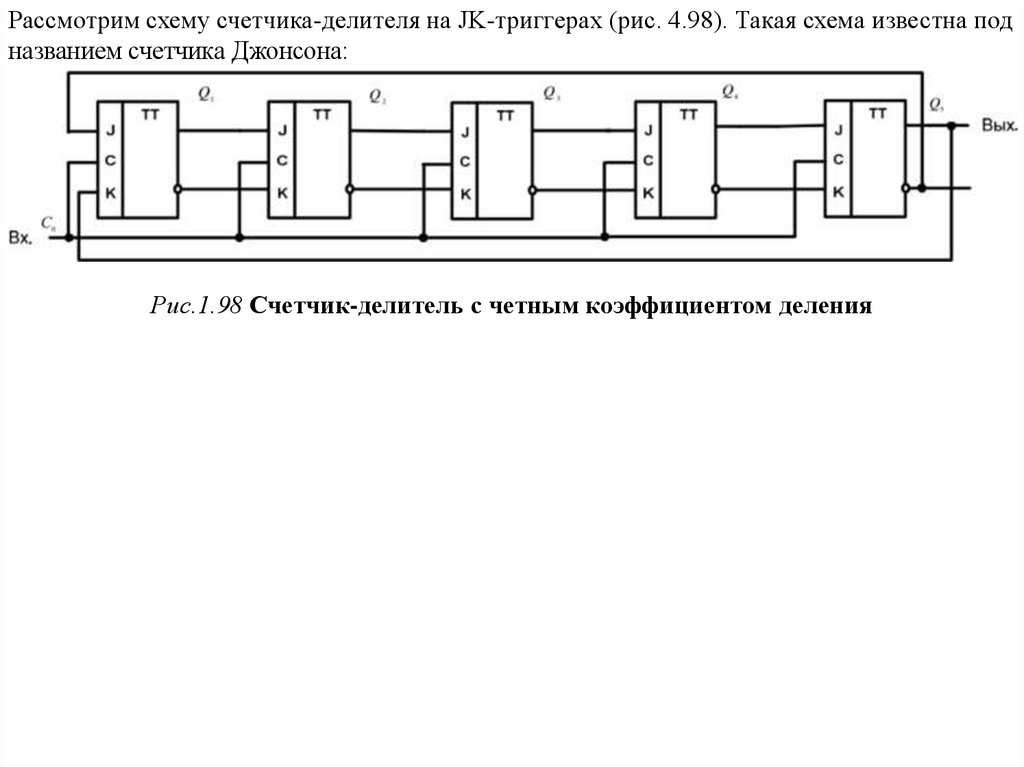
Рассмотрим схему счетчика-делителя на JK-триггерах (рис. 4.98). Такая схема известна подназванием счетчика Джонсона:
Рис.1.98 Счетчик-делитель с четным коэффициентом деления
31.
Логика работы:Пусть все триггеры находятся в нулевом состоянии Qi=Q2=Q3=Q4=Q5=0. Тогда J1=QS=1,
Ki=Q5=0. С приходом 1-го входного импульса триггер Ti перейдет в состояние Q=l,
остальные триггеры останутся в состоянии Q=0, так как все они двухступенчатой
структуры. С приходом 2-го входного импульса триггер Ti останется в состоянии Qi=l, т.к.
по-прежнему Ji=Q5 =1.
Триггер Т2 перейдет в состояние Q2=l и т.д. С приходом 5-го счетного импульса все
триггеры перейдут в состояние Q=l. Тогда Ji=Q5 =0, Ki=Q5=1. Шестым импульсом триггер
Т| перейдет в состояние Q=0. Остальные триггеры останутся в состоянии Q=l. С приходом
7-го импульса состояние триггеров будет: Qi=0, Q2=0, Q3=l, Q4=l, Q5=l и т.д. После прихода
10-го импульса счетчик прейдет в состояние Qi=0, i=l,5 и счет начинается сначала. Таким
образом, Kc4=2N=10. Выходные импульсы снимаются с Q5 (выход 1). Последовательность
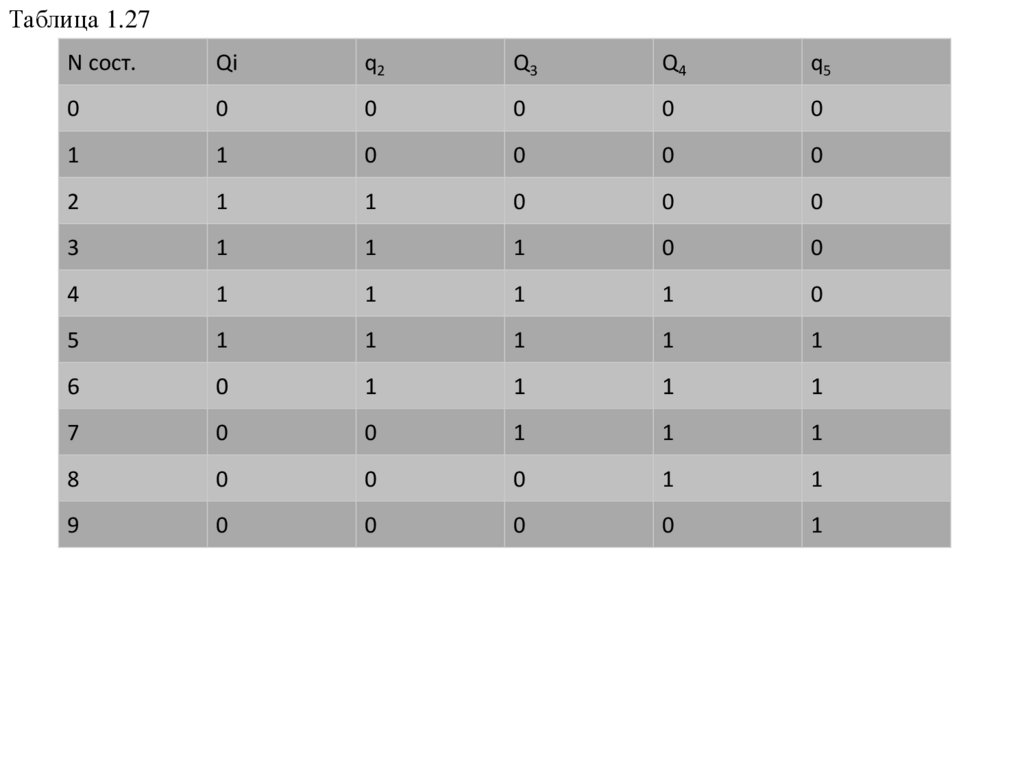
состояний приведена в таблице 1.27.
32.
Таблица 1.27N сост.
Qi
q2
Q3
Q4
q5
0
0
0
0
0
0
1
1
0
0
0
0
2
1
1
0
0
0
3
1
1
1
0
0
4
1
1
1
1
0
5
1
1
1
1
1
6
0
1
1
1
1
7
0
0
1
1
1
8
0
0
0
1
1
9
0
0
0
0
1
33.
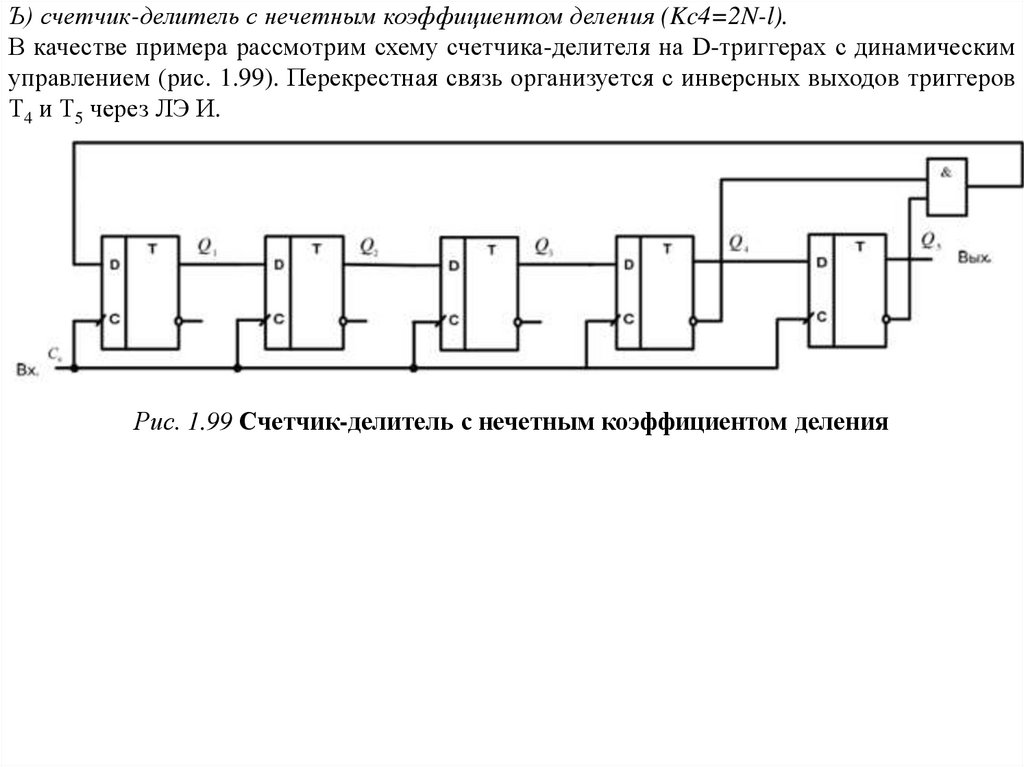
Ъ) счетчик-делитель с нечетным коэффициентом деления (Kc4=2N-l).В качестве примера рассмотрим схему счетчика-делителя на D-триггерах с динамическим
управлением (рис. 1.99). Перекрестная связь организуется с инверсных выходов триггеров
Т4 и Т5 через ЛЭ И.
Рис. 1.99 Счетчик-делитель с нечетным коэффициентом деления
34.
Пусть в исходном состоянии все триггеры счетчика находятся в состоянии 0. ТогдаDi=Q4Q5=11=1. С приходом 1-го входного импульса триггер Ti перейдет в состояние Qi=l.
Остальные триггеры останутся в состоянии «О».
С приходом 2-го входного импульса триггер Ti останется в состоянии Qi=l, так как Dj=l, а
триггер Т2 перейдет в состояние Q2=l и т.д. Состояния от нулевого до четвертого будут
устанавливаться обычным образом (таблица №4.27).
С установлением четвертого состояния Q4=l (Q4=0) на входе триггера Ti D,=Q4Q5 =0-1=0 и
с приходом очередного (пятого) входного импульса триггер Т| перейдет в состояние Qi=0.
Таким образом, после 4-го состояния (11110) регистр перейдет в 6-е состояние (01111) и
далее переходы будут обычными. Состояние (11111) исключается и поэтому Kc4=2N-l=2-5l=9. Аналогичным путем можно исключить состояние 11111... 11 в делителе с любым
числом разрядов.
Достоинства счетчика-делителя на регистрах с перекрестной связью:
- наращиваемость схемы;
- разрядность регистра не связана с быстродействием, так как он состоит из однотипных
триггеров и нет цепей переноса.












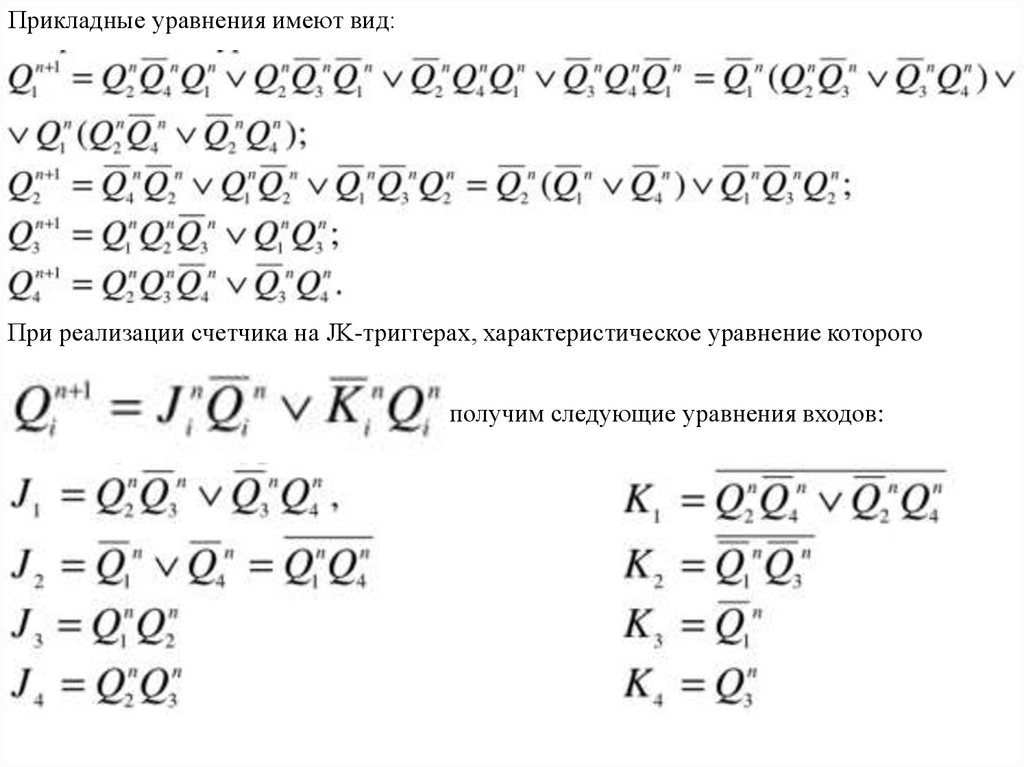



 electronics
electronics








