Similar presentations:
Автоматизированная система прогнозирования финансовых временных рядов с применением многослойного персептрона
1. Автоматизированная система прогнозирования финансовых временных рядов с применением многослойного персептрона
Выпускная квалификационная работа бакалавраВыполнила:
студентка группы 6402 Хохлова В.С.
Руководитель работы:
к.т.н. доцент Лёзина И.В.
Самара 2012
2. Функции системы
• Автоматизация процесса прогнозированияфинансовых временных рядов
• Обеспечение графического представления
данных прогнозирования
• Сохранение и загрузка обученной сети
• Возможность дообучения сети на новых
данных
2
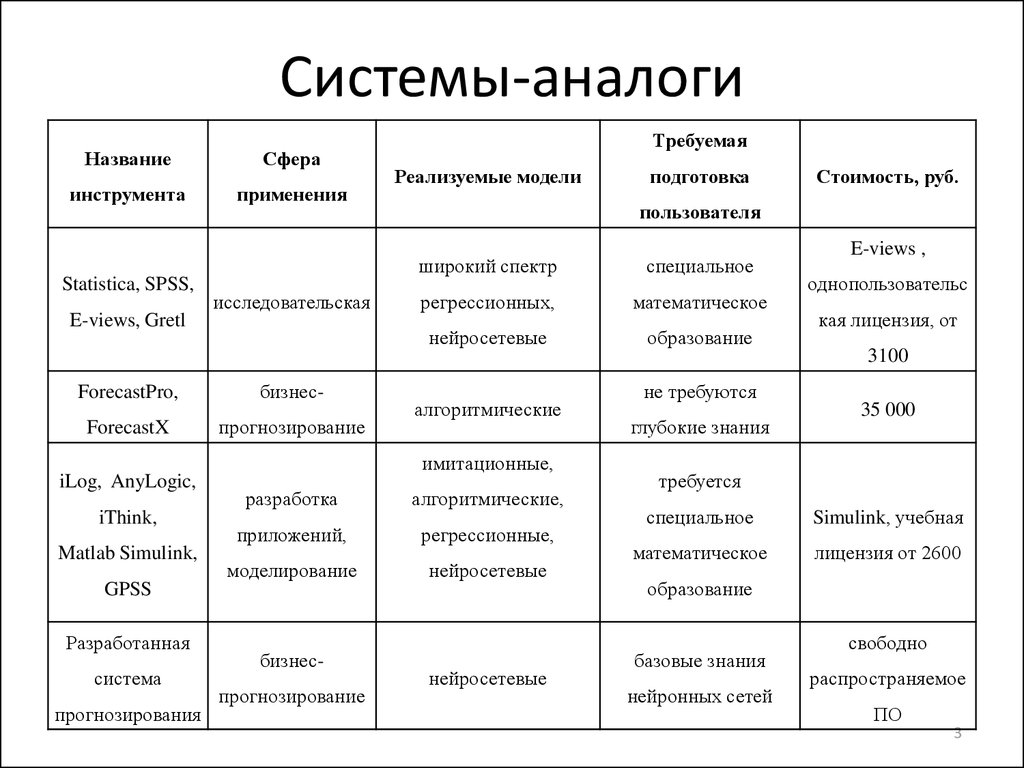
3. Системы-аналоги
НазваниеСфера
инструмента
применения
Statistica, SPSS,
E-views, Gretl
исследовательская
ForecastPro,
бизнес-
ForecastX
прогнозирование
iLog, AnyLogic,
iThink,
Matlab Simulink,
GPSS
Разработанная
система
прогнозирования
Требуемая
Реализуемые модели
широкий спектр
специальное
регрессионных,
математическое
нейросетевые
образование
алгоритмические
разработка
алгоритмические,
приложений,
регрессионные,
моделирование
нейросетевые
прогнозирование
Стоимость, руб.
пользователя
имитационные,
бизнес-
подготовка
нейросетевые
не требуются
глубокие знания
E-views ,
однопользовательс
кая лицензия, от
3100
35 000
требуется
специальное
Simulink, учебная
математическое
лицензия от 2600
образование
базовые знания
нейронных сетей
свободно
распространяемое
ПО
3
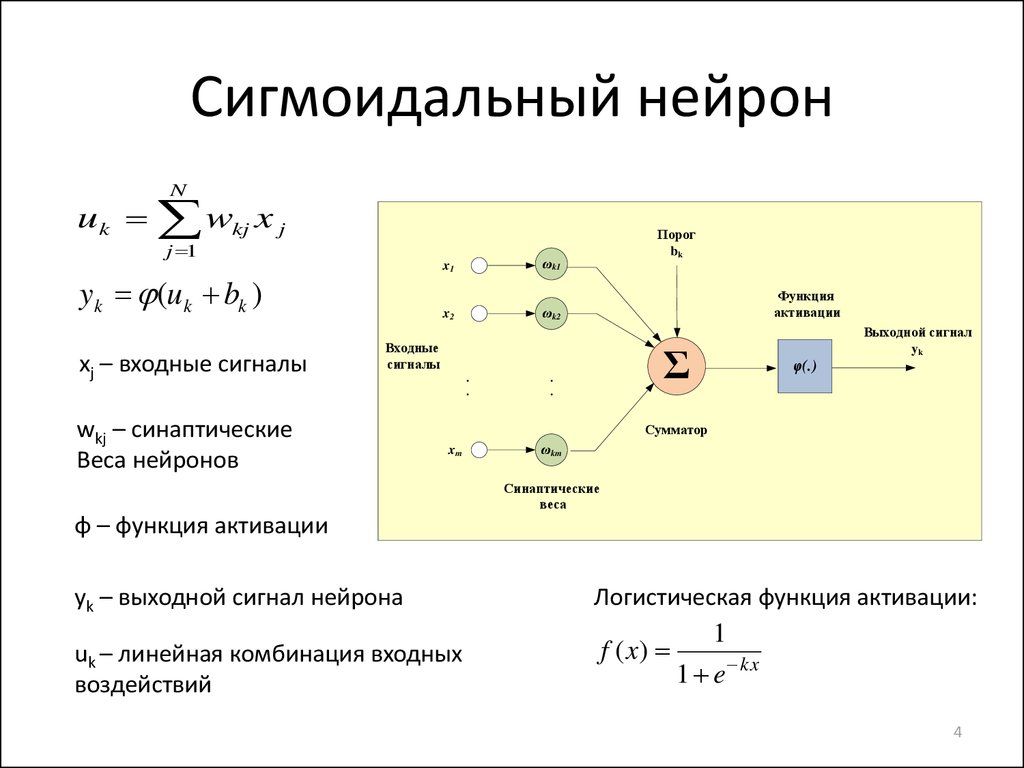
4. Сигмоидальный нейрон
Nu k wkj x j
j 1
yk (uk bk )
xj – входные сигналы
x1
ωk1
x2
ωk2
Порог
bk
Функция
активации
Входные
сигналы
wkj – синаптические
Веса нейронов
.
.
Σ
.
.
Выходной сигнал
yk
φ(.)
Сумматор
xm
ωkm
Синаптические
веса
φ – функция активации
yk – выходной сигнал нейрона
Логистическая функция активации:
uk – линейная комбинация входных
воздействий
f ( x)
1
1 e kx
4
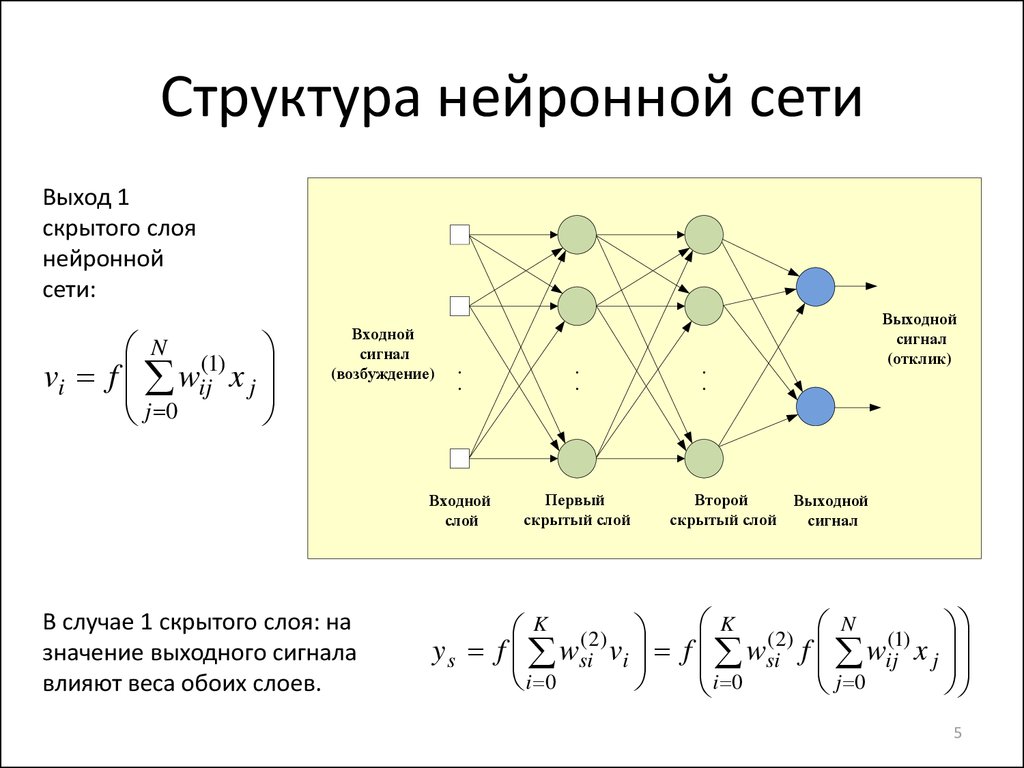
5. Структура нейронной сети
Выход 1скрытого слоя
нейронной
сети:
N (1)
vi f wij x j
j 0
Входной
сигнал
(возбуждение)
В случае 1 скрытого слоя: на
значение выходного сигнала
влияют веса обоих слоев.
.
.
.
.
Входной
слой
Первый
скрытый слой
Выходной
сигнал
(отклик)
.
.
Второй
скрытый слой
K ( 2)
y s f wsi vi
i 0
Выходной
сигнал
K ( 2) N (1)
f wsi f wij x j
j 0
i 0
5
6. Градиентный метод обучения: алгоритм наискорейшего спуска
N{(
x
(
n
),
d
(
n
)))}
1
n 1
2
x(n) – входные данные, d(n) - желаемый отклик
Прямой проход
Индуцированные локальные поля нейронов: v (jl )
Выходные сигналы:
Ошибка:
3
y (jl ) (n) j ( j (n)),
(l )
( l 1)
w
(
n
)
y
ji
i ( n)
i
y (j0) (n) x j (n).
e j ( n) d j ( n) o j ( n)
Обратный проход
Локальные градиенты:
e(j L ) (n) 'j (v (j L ) (n))
(j l ) (n) ' (v (l ) (n)) (l 1) (n) (l 1) (n)
k
kj
j j
k
Изменение весов: w(jil ) (n 1) w(jil ) (n) [w(jil ) (n 1)] (j l ) (n) y (jl 1) (n)
6
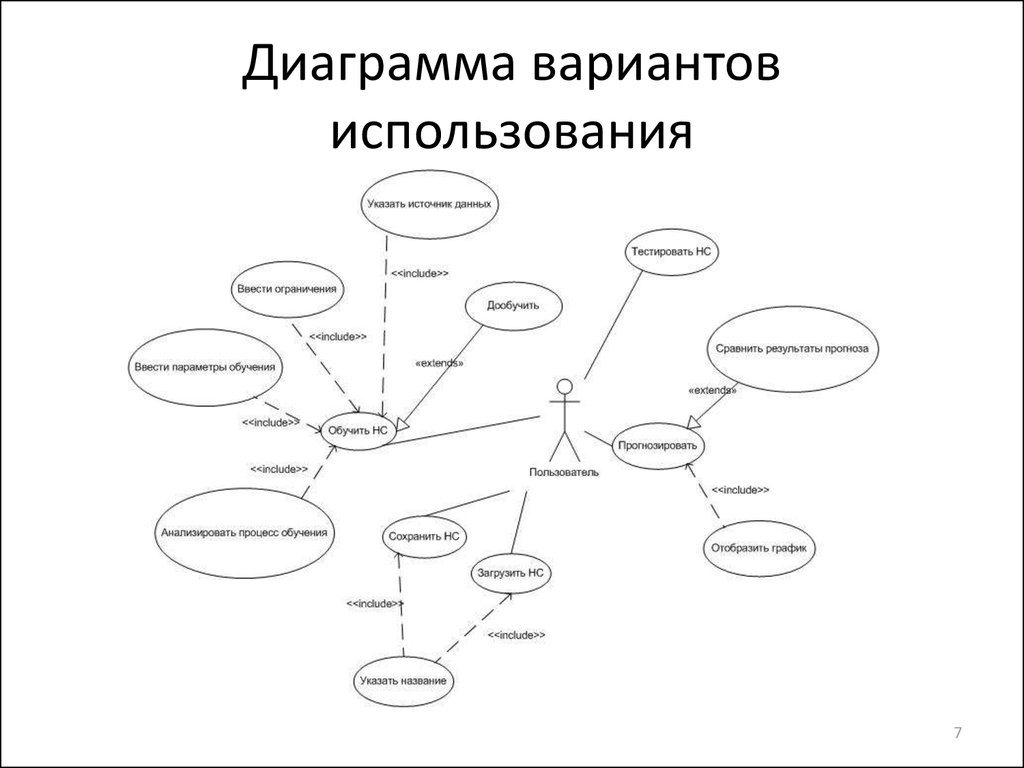
7. Диаграмма вариантов использования
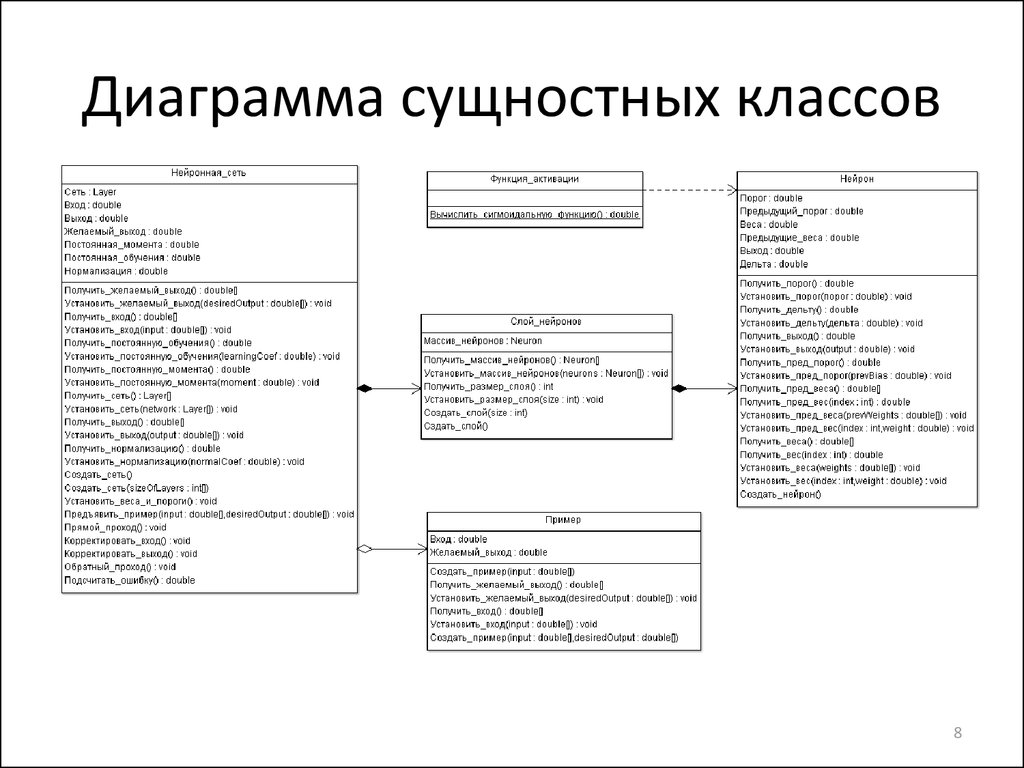
78. Диаграмма сущностных классов
89. Индекс Доу-Джонса
Доу-Джонс является старейшимсреди существующих
американских рыночных индексов.
Этот индекс был создан для
отслеживания развития
промышленной составляющей
американских фондовых рынков.
Индекс охватывает 30 крупнейших
компаний США. Приставка
«промышленный» является данью
истории — в настоящее время
многие из компаний, входящих в
индекс, не принадлежат к этой
отрасли.
9
10. Тестирование нейронной сети
Для обучения и тестирования сети прогнозирования индекса Доу-Джонсаиспользовались выборка значений индекса за период с 26.01.2012 по
26.03.2012.
Значения за первый месяц использовались для обучения нейронной сети,
значения второго месяца использовались для тестирования сети.
Среднеквадратическое отклонение (СКО)
рассчитывалось по формуле:
_
1 n
2
(
x
x
)
i
n i 1
xi – значение, которое спрогнозировала сеть
x – фактическое значение
n – количество примеров тестирования
10
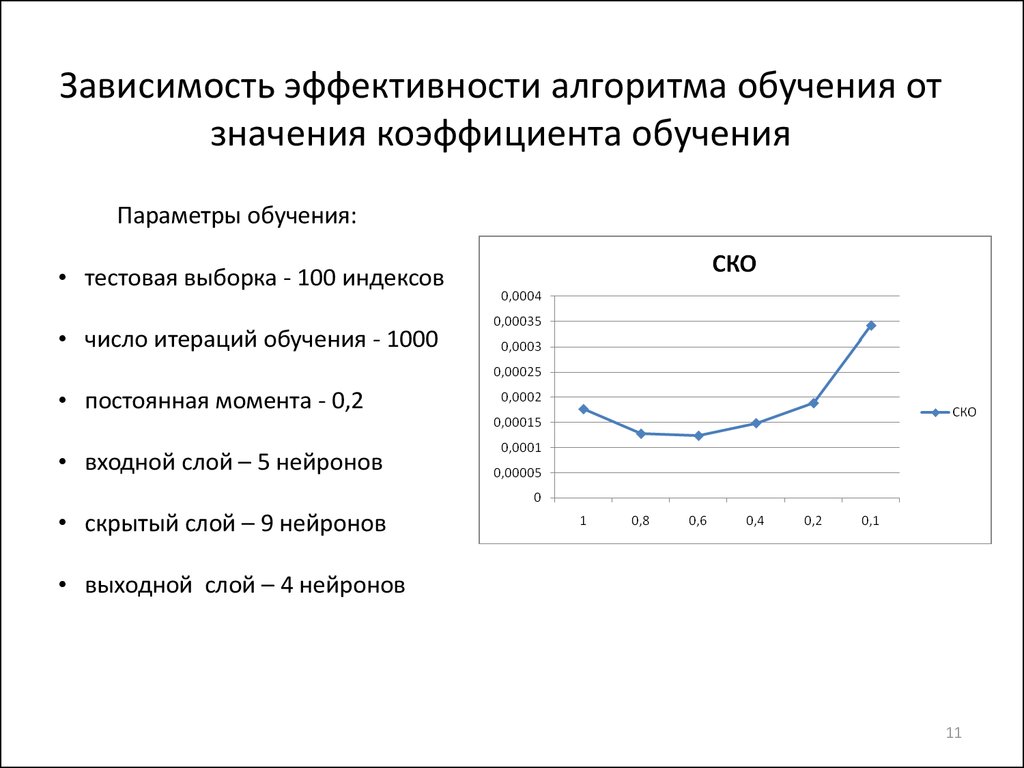
11. Зависимость эффективности алгоритма обучения от значения коэффициента обучения
Параметры обучения:• тестовая выборка - 100 индексов
• число итераций обучения - 1000
• постоянная момента - 0,2
• входной слой – 5 нейронов
• скрытый слой – 9 нейронов
• выходной слой – 4 нейронов
11
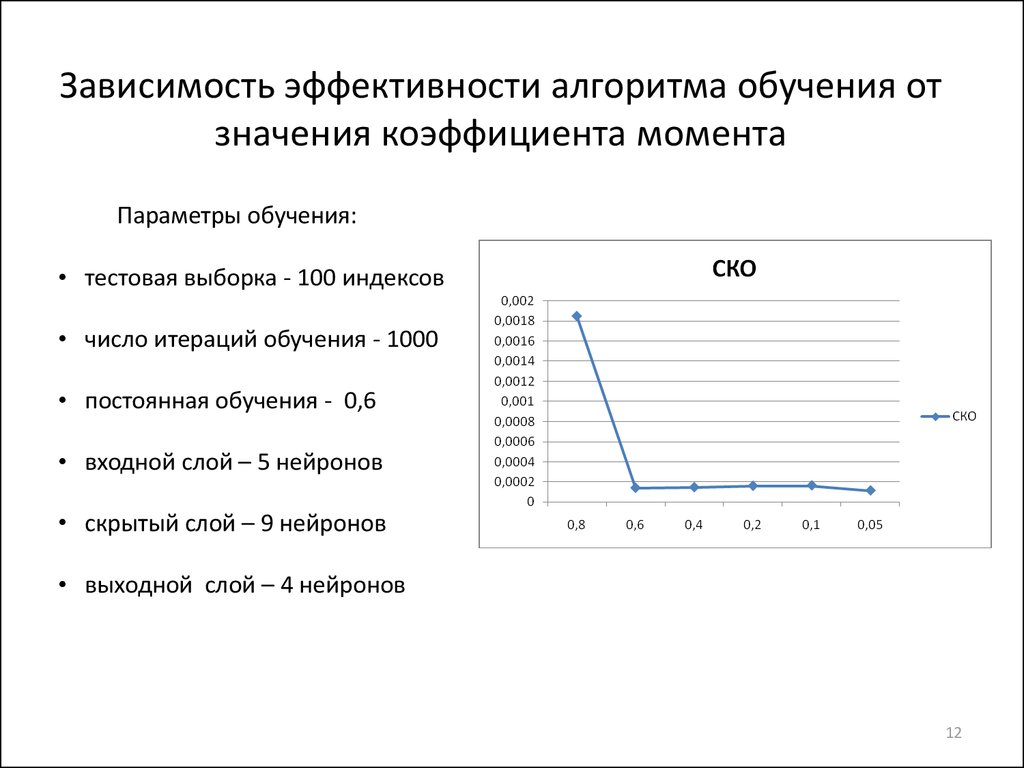
12. Зависимость эффективности алгоритма обучения от значения коэффициента момента
Параметры обучения:• тестовая выборка - 100 индексов
• число итераций обучения - 1000
• постоянная обучения - 0,6
• входной слой – 5 нейронов
• скрытый слой – 9 нейронов
• выходной слой – 4 нейронов
12
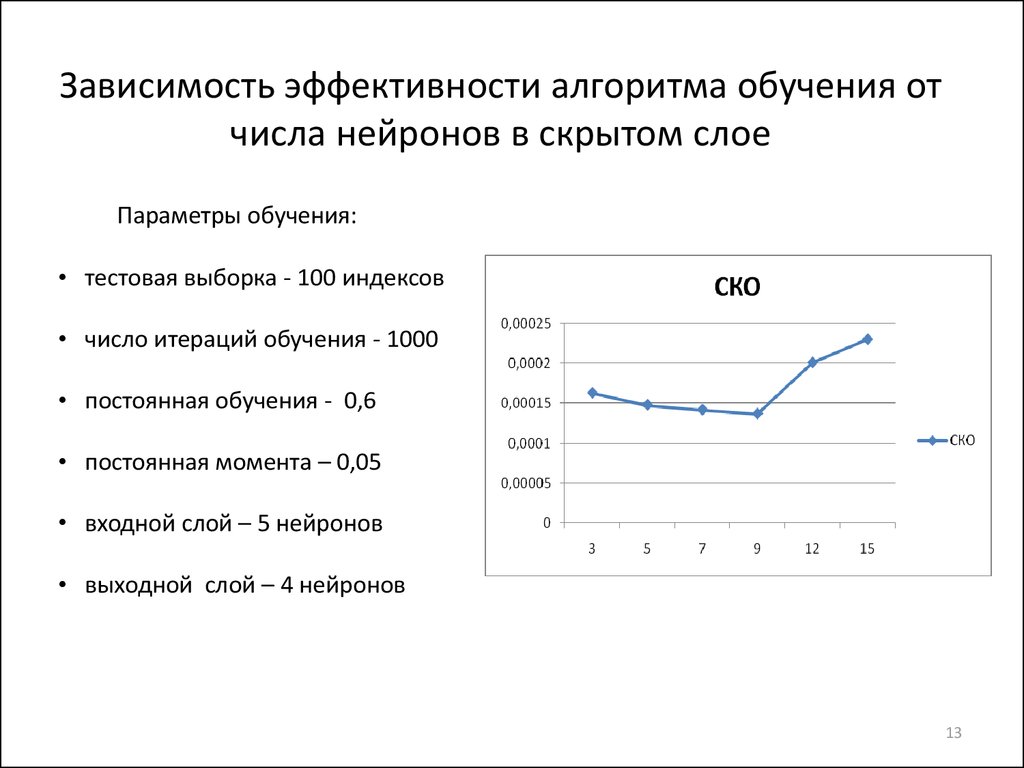
13. Зависимость эффективности алгоритма обучения от числа нейронов в скрытом слое
Параметры обучения:• тестовая выборка - 100 индексов
• число итераций обучения - 1000
• постоянная обучения - 0,6
• постоянная момента – 0,05
• входной слой – 5 нейронов
• выходной слой – 4 нейронов
13
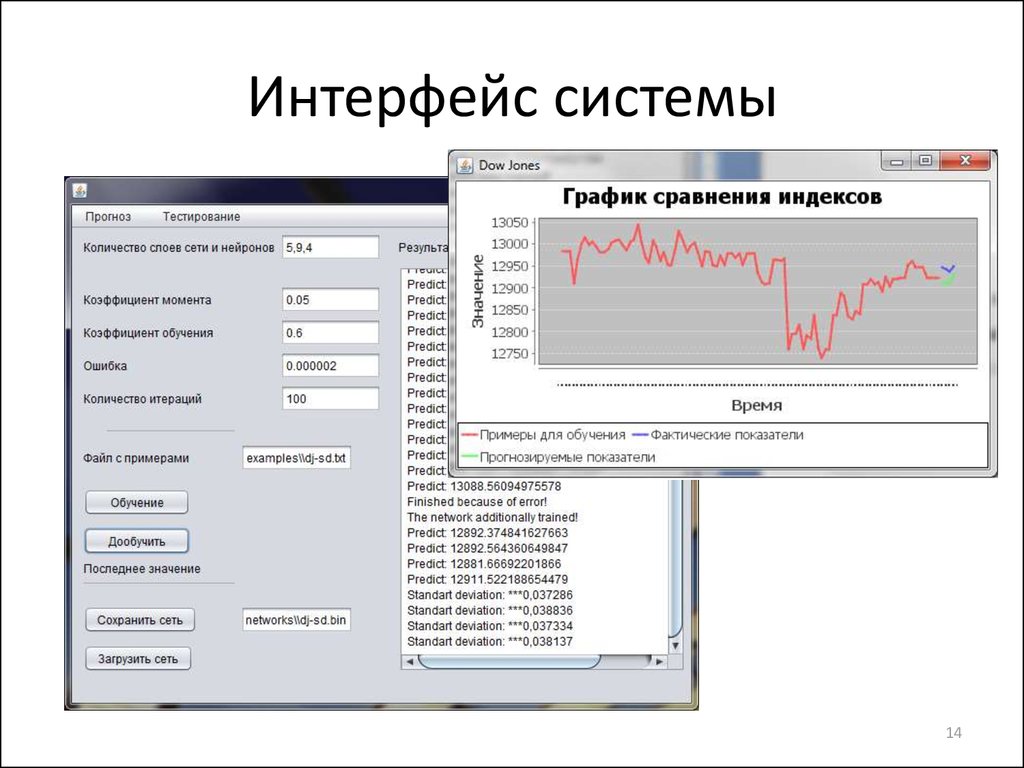
14. Интерфейс системы
1415. Результат прогноза
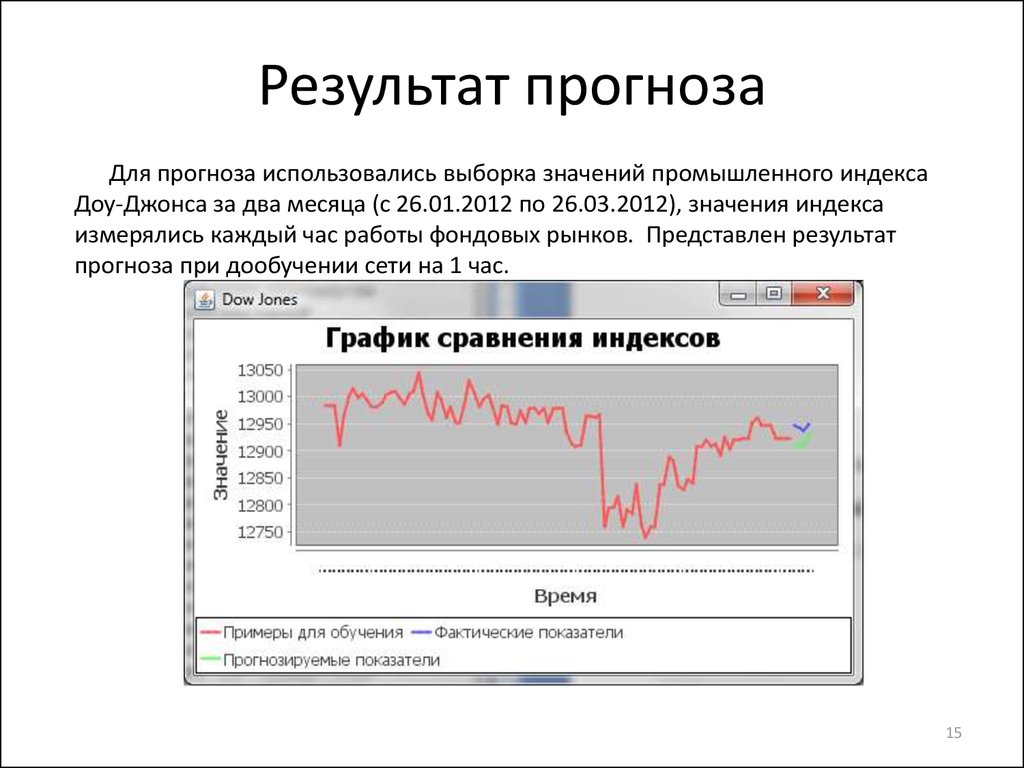
Для прогноза использовались выборка значений промышленного индексаДоу-Джонса за два месяца (с 26.01.2012 по 26.03.2012), значения индекса
измерялись каждый час работы фондовых рынков. Представлен результат
прогноза при дообучении сети на 1 час.
15
16. Заключение
• Разработана автоматизированная система прогнозированияфинансовых временных рядов с применением многослойного
персептрона
• На основе анализа предметной области разработана
информационно-логическая модель автоматизированной
системы в нотации UML
• Программное обеспечение системы разработано на язые Java
в среде NetBeans IDE 7.1.1 под управлением ОС Windows ХР
• Проведены исследования по обучению сети с различными
параметрами обучения и структурой сети, определены
оптимальные значения параметров сети для поставленной
задачи
16






 finance
finance software
software








