Комбинаторные методы решения оптимизационных задач (лекция 2)

1.

МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
ЛЕКЦИЯ 2
КОМБИНАТОРНЫЕ МЕТОДЫ
РЕШЕНИЯ ОПТИМИЗАЦИОННЫХ
ЗАДАЧ

2.

Цель: освоение навыков решения
оптимизационных задач комбинаторными
методами.
Задачи:
•изучение особенностей применения
комбинаторных алгоритмов решения
оптимизационных задач;
•изучение теоретических основ
комбинаторных алгоритмов;

3.

КОМБИНАТОРНЫЕ МЕТОДЫ РЕШЕНИЯ
ОПТИМИЗАЦИОННЫХ ЗАДАЧ
Генерация подмножеств заданного множества:
- разработка генератора подмножеств на С++;
- решение задачи о рюкзаке.
Генерация сочетаний:
- разработка генератора сочетаний на С++;
- решение задачи об оптимальной загрузке.
Генерация перестановок:
- разработка генератора перестановок на С++;
- решение задачи о коммивояжере.
Генерация размещений:
- разработка генератора размещений на С++;
- решение задачи об оптимальной загрузке (с центровкой)

4.

Комбинаторный анализ (комбинаторика,
комбинаторная математика) – раздел
математики, посвященный решению задач
выбора
и
расположения
элементов
некоторого, обычно конечного, множества в
соответствии с заданными правилами.

5.

Предприятие может предоставить работу по
одной специальности 4 женщинами, по
другой - 6 мужчинам, по третьей - 3
работникам независимо от пола. Сколькими
способами можно заполнить вакантные
места, если имеются 14 претендентов: 6
женщин и 8 мужчин?

6.

Сколько различных дробей
можно составить из чисел 3, 5,
7, 11, 13, 17 так, чтобы в
каждую дробь входили 2
различных числа? Сколько
среди них будет правильных
дробей?

7.

КОМБИНАТОРИКА
m
An из n элементов по m (n > m) называют
Размещениями
их соединения, каждое из которых содержит ровно m
различных элементов (выбранных из данных n элементов) и
которые отличаются либо сами элементами, либо порядком
элементов.
n!
A n ( n 1)( n 2)...( n ( m 1))
( n m )!
m
n
Соединения из n элементов, каждое из которых
содержит все n элементов, и которые отличаются лишь
порядком элементов, называются перестановками Pn.
n
Pn An n!

8.

Комбинаторика
КОМБИНАТОРИКА
m
C
Сочетаниями
из n элементов по m (n > m)
n
называют их соединения, каждое из которых содержит
ровно m различных элементов (выбранных из данных n
элементов) и которые отличаются хотя бы одним
элементом.
m
A
n!
m
m
m
m
n
Cn m! An Cn
Cn
m!
m!(n m)!
Числа Cnm являются коэффициентами в формуле
бинома Ньютона:
n
(a b) n a n Cn1a n 1b Cn2 a n 2b 2 ... Cnnb n Cnk a n k b k
k 0

9.

Комбинаторика
КОМБИНАТОРИКА
Свойства сочетаний:
1
0
n
Cn n; Cn Cn 1;
m
n m
Cn Cn , m 0,1,2,..., n;
0
1
2
n
n
n
n
n
n
0
1
2
n
n
n
n
n
n
C nm С nm 11 C nm 1 .
C C C ... C 2 ;
C C C ... ( 1) C 0;
Сnm 11 Cnm 1
(n 1)!
(n 1)!
(m 1)! (n m)! m! (n m 1)!
(n 1)!
1
(n 1)!
n
1
Cnm
(m 1)! (n m 1)! n m m (m 1)! (n m 1)! (n m) m

10.

КОМБИНАТОРИКА.
Треугольник паскаля

11.

Комбинаторика
КОМБИНАТОРИКА
Tреугольник Паскаля:
1
C00
1 1
C10 C11
0
1
2
1 2 1
C2 C2 C2
C30 C31 C32 C33
1 3 3 1
0
1
2
3
4
C4 C4 C4 C4 C4
1 4 6 4 1
0
1
2
3
4
5
C5 C5 C5 C5 C5 C5
1 5 10 10 5 1

12.

Генерация множества всех подмножеств
X {x1 , x2 , ..., xn }
X n
2
X
2
X
2 .
n
Алгоритм генерации множества всех
подмножеств основывается на взаимно
однозначном соответствии между элементами
булеана 2 X множества X и всеми целыми
числами множества {0,1, ..., 2|X | 1} , записанными в
двоичном виде. Следует сказать, что алгоритм
имеет сложность O(2| X | ) и поэтому реально может
применяться для множеств с небольшой
мощностью.

13.

Построение элементов булеана множества Х сводится к
следующему алгоритму:
1. Пронумеровать элементы заданного множества X , начиная с нуля.
2. Сформировать битовую последовательность B {bi }, состоящую из
B X двоичных нулей. Пронумеровать элементы этой последовательности
справа налево, начиная с нуля.
X
3. Последовательно выполнить шаги 4 и 5 алгоритма 2 раз.
4. Выбрать из множества X элементы с номерами i , для которых bi 1.
Полученное подмножество будет являться элементом булеана 2 X . В первом
случае не будет выбран ни один элемент (пустое подмножество) множества
X , так как исходная последовательность B состоит только из нулей.
5. Интерпретируя
битовую
последовательность
как
целое
положительное число, увеличить это число на единицу.

14.

Пример построения булеана для множества
X {a, b, c, d }.
Под элементами множества X изображен столбец битовых
последовательностей. Каждая строка столбца соответствует
состоянию
последовательности
B
при
очередном
прохождении шага 4 алгоритма. Слева от столбца указаны
целые числа, которые являются интерпретацией битовых
последовательностей как целых чисел в десятичной системе
счисления.
Стрелки на рисунке указывают на строки другого столбца,
который содержит элементы множества X соответствующие
битовым последовательностям. Каждая строка этого столбца
содержит элементы одного из подмножеств множества X

15.

3 2 1 0
a b c d
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
X {a, b, c, d }.
d
c
c d
b
b
d
b c
b c d
a
a
a
a
a
a
a
a
d
c
c d
b
b
d
b c
b c d

16.

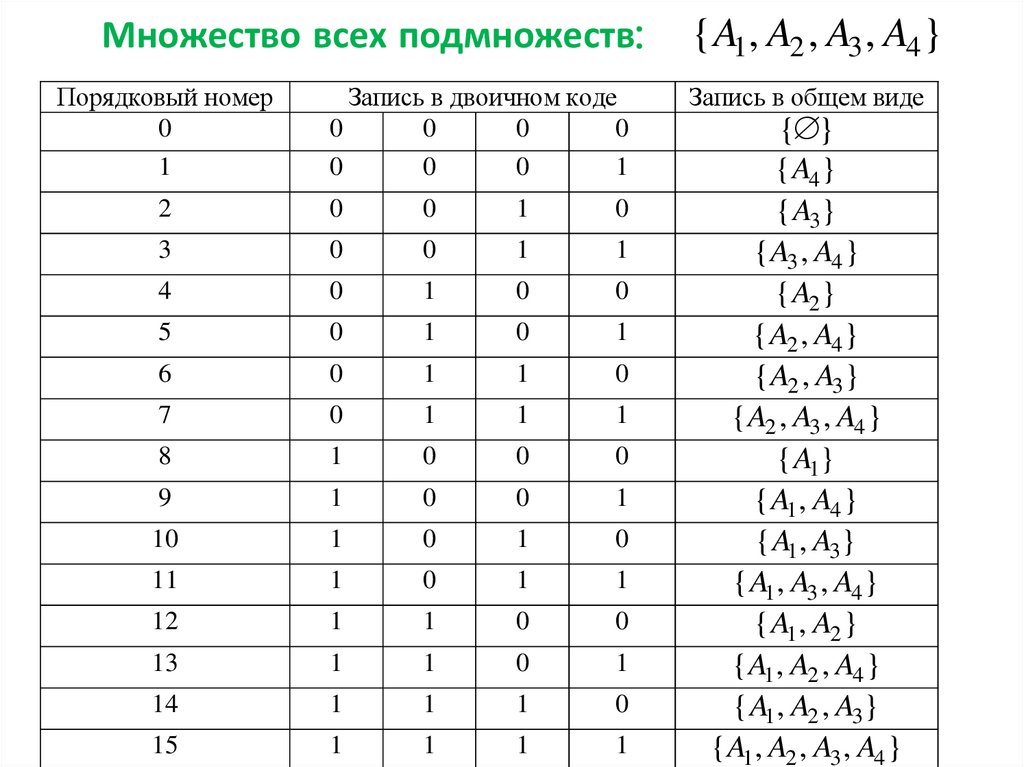
Множество всех подмножеств:
Порядковый номер
0
1
Запись в двоичном коде
0
0
0
0
0
0
0
1
2
0
0
1
0
3
0
0
1
1
4
0
1
0
0
5
0
1
0
1
6
0
1
1
0
7
0
1
1
1
8
1
0
0
0
9
1
0
0
1
10
1
0
1
0
11
1
0
1
1
12
1
1
0
0
13
1
1
0
1
14
1
1
1
0
15
1
1
1
1
{ A1 , A2 , A3 , A4 }
Запись в общем виде
{ }
{ A4 }
{ A3}
{ A3 , A4 }
{ A2 }
{ A2 , A4 }
{ A2 , A3}
{ A2 , A3 , A4 }
{ A1}
{ A1 , A4 }
{ A1 , A3}
{ A1 , A3 , A4 }
{ A1 , A2 }
{ A1 , A2 , A4 }
{ A1 , A2 , A3}
{ A1 , A2 , A3 , A4 }

17.

Принципы реализации генератора на С++
1. Все генераторы должны иметь одинаковый
интерфейс
2. Должна быть возможность применения нескольких
генераторов одновременно.
3. Функции должны легко встраиваться в другие.
Генератор реализован в виде структуры subset.
Применение структуры позволяет создавать несколько
экземпляров одного генератора и упростить его вызов
в других программах.
Структура subset имеет единственный конструктор,
параметром которого является мощность исходного
множества.

18.

Принципы реализации генератора на С++
Для хранения текущего состояния
генератора
используются переменные:
• n (мощность исходного множества, которая не
должна превышать 63),
• sn (текущее количество элементов массива
индексов),
• sset (адрес нулевого элемента массива индексов) и
mask (битовая последовательность).
Первоначальное
значение
всех
переменных
инициализируются конструктором. Причем значения n
и sset после инициализации остаются неизменными, а
значения остальных переменных меняются в процессе
работы генератора.

19.

Принципы реализации генератора на С++
Помимо конструктора, структура содержит еще пять функцийчленов.
Функция getfirst позволяет заполнить массив индексов в
соответствии с текущим значением битовой последовательности
mask. Функция устанавливает значение sn, равным количеству
двоичных единиц в последовательности mask, а в массив sset,
начиная с нулевого элемента, записывает номера единичных
позиций
(позиции
нумеруются
справа
налево)
в
последовательности mask. Вызов функции сразу после создания
структуры приводит к установке значения
sn в нуль, что
соответствует битовой последовательности mask, состоящей из
одних нулей (конструктор инициализирует mask нулевым
значением). Функция getfirst всегда возвращает значение sn.
Обычно пользователь эту функцию вызывает один раз – для
формирования первого (пустого) подмножества. Для получения
остальных подмножеств применяется функция getnext.

20.

Пример применения
генератора множества всех подмножеств
Помимо конструктора, структура содержит еще пять функцийчленов.
В качестве исходного множества в примере используется строковый
массив, состоящий из четырех строк. Вначале этот массив
распечатывается. Затем объявляется структура subset и ей в качестве
параметра передается количество элементов исходного множества.
Цикл формирования подмножеств начинается функцией
getfirst, которая формирует первый (пустой) массив sset,
соответствующий пустому подмножеству. Все остальные массивы
индексов (для непустых подмножества) формируются функцией
getnext. Выход из цикла происходит после того, как getnext
возвращает отрицательное значение (получены все подмножества).
Выбор элементов исходного массива осуществляется с помощью
функции ntx.

21.

// Combi.h
#pragma once
namespace combi
{
struct subset
// генератор множества всех подмножеств
{
short n,
// количество элементов исходного множества < 64
sn,
// количество элементов текущего подмножества
*sset;
// массив индексов текущего подмножества
unsigned __int64 mask; // битовая маска
subset(short n = 1); // конструктор(количество элементов исходного
множества)
short getfirst();
// сформормировать массив индексов по битовой маске
short getnext();
// ++маска и сформировать массив индексов
short ntx(short i);
// получить i-й элемент массива индексов
unsigned __int64 count(); // вычислить общее количество подмножеств
void reset();
// сбросить генератор, начать сначала
};
};

22.

// Combi.cpp
#include "stdafx.h"
#include "Combi.h"
#include <algorithm>
namespace combi
{
subset::subset(short n)
{
this->n = n;
this->sset = new short[n];
this->reset();
};
void subset::reset()
{
this->sn = 0;
this->mask = 0;
};

23.

short subset::getfirst()
{
__int64 buf = this->mask;
this->sn = 0;
for (short i = 0; i < n; i++)
{ if (buf & 0x1) this->sset[this->sn++] = i;
buf >>= 1;
}
return this->sn;
};
short subset::getnext()
{
int rc = - 1;
this->sn = 0;
if (++this->mask < this->count()) rc = getfirst();
return rc;
};
short subset::ntx(short i)
{return this->sset[i];};
unsigned __int64 subset::count()
{return (unsigned __int64)(1<<this->n);}; };

24.

Решение упрощенной задачи о рюкзаке с помощью
генератора множества всех подмножеств
Существует n различных предметов, характеризующихся объемом vi и
стоимостью vi ci , i 1, n . Необходимо выбрать несколько разных предметов
таким способом, чтобы они поместились в рюкзаке объемом V и при этом их
суммарная стоимость была максимальной.
Математическая модель задачи
n
xi vi ci max,
i 1
n
xi vi V ,
i 1
xi {0, 1},
где xi – неизвестные, которые требуется найти.
i 1, n.

25.

Решение упрощенной задачи о рюкзаке с помощью
генератора множества всех подмножеств
Решением задачи при такой постановке будет вектор ( x1 , x2 , ..., xn ) .
Каждый элемент xi вектора может принимать значение 0 или 1.
При этом если xi =0 то i -ый предмет не выбран, и если xi =1 то i -й
предмет выбран для размещения в рюкзаке.
Задача имеет следующие исходные данные:
V=100 – вместимость (объем) рюкзака;
n=4 – количество предметов;
(25, 30, 60, 20) – вектор объемов предметов;
(25, 10, 20, 30) – вектор стоимостей предметов.
С помощью генератора всех подмножеств последовательно
генерируются все массивы индексов (второй слева столбец),
соответствующие битовой последовательности (первый столбец
слева). На основе массивов индексов формируются все
возможные подмножества предметов.

26.

Решение упрощенной задачи о рюкзаке с помощью
генератора множества всех подмножеств
Для каждого подмножества вычисляется суммарный объем
(столбец с заголовком ∑vi) и сверяется с вместимостью
рюкзака.
Если выбранное подмножество предметов помещается в
рюкзак (суммарный объем предметов не превышает
вместимости рюкзака V=100), то для выбранных предметов
рассчитывается суммарная стоимость (столбец ∑vici).
Окончательным решением задачи будет подмножество
предметов, имеющее максимальную суммарную стоимость
при допустимом суммарном объеме.
Строка, соответствующая решению, отмечена рамкой.

27.

i
4
3
2
1
vi
20 60 30 25
V 100
ci
4
3
2
1
0
0
0
0
0
1
0
0
0
1
2
0
0
1
0
2
3
0
0
1
1
2
4
0
1
0
0
3
5
0
1
0
1
3
6
0
1
1
0
3
2
7
0
1
1
1
3
2
8
1
0
0
0
4
9
1
0
0
1
4
10
1
0
1
0
4
2
11
1
0
1
1
4
2
12
1
1
0
0
4
3
13
1
1
0
1
4
3
14
1
1
1
0
4
3
2
15
1
1
1
1
4
3
2
i
30 20 10 25
1
1
1
1
1
1
1
vi
vi ci
0
0
25
625
30
300
55
925
60
1200
85
1825
90
1500
115
20
600
45
1225
50
900
75
1525
80
1800
105
110
1
135

28.

Пример реализации функции knapsack_s на языке C++,
которая решает задачу о рюкзаке.
Функция knapsack_s имеет четыре входных параметра, задающих
условие задачи: V (объем рюкзака), n (количество предметов), v
(массив размерностью n, содержащий объемы всех предметов), c
(массив размерностью n, содержащий стоимости всех предметов), а
также один выходной параметр m (массив размерностью n). Каждый
элемент массива m может быть только единицей или нулем. Единица
указывает, что соответствующий предмет включен, а ноль – не
включен в оптимальный перечень предметов. В результате
выполнения функция возвращает оптимальную стоимость рюкзака, т.
е. максимальную суммарную стоимость предметов, которые можно
одновременно поместить в рюкзак заданной вместимости.
В процессе своей работы функция knapsack_s использует
генератор множества всех подмножеств (combi::subset) и
вызывает три вспомогательные функции: calcv, calcc и setm.

29.

Пример реализации функции knapsack_s на языке C++,
которая решает задачу о рюкзаке.
Для подключения генератора в заголовочный файл функции
knapsack_s добавлена директива include, которая включает
файл Combi.h, содержащий шаблон структуры combi::subset.
Функция calcv предназначена для вычисления суммарного
объема текущего подмножества предметов. Она принимает
два входных параметра: s (структуру combi::subset) и v
(массив размерностью n, содержащий объемы всех
предметов), а также возвращает суммарный объем текущего
подмножества предметов.
Функция calcс позволяет вычислить суммарную стоимость
текущего подмножества предметов. Она принимает два
входных параметра: s (структуру combi::subset) и c (массив
размерностью n, содержащий стоимости всех предметов), а
возвращает суммарную стоимость текущего подмножества
предметов.

30.

Пример реализации функции knapsack_s на языке C++,
которая решает задачу о рюкзаке.
Функция setm принимает два параметра: входной s
(структуру combi::subset) и возвращаемый m (массив
размерностью n, содержащий нули и единицы).
Функция knapsack_s перебирает все подмножества
множества предметов (функции getfirst и getnext
генератора), вычисляет суммарный объем (функция calcv)
каждого подмножества, для подмножества с суммарным
объемом, меньшим V, рассчитывает суммарную стоимость
(функция calcc) и запоминает (и возвращает) оптимальный
вариант (формирует выходной массив m с помощью
функции setm).

31.

Пример реализации функции knapsack_s на языке C++,
которая решает задачу о рюкзаке.
Оценить зависимость продолжительности вычисления
оптимальной комбинации предметов от их общего количества
можно с помощью следующей программы.
Для вычисления продолжительности выполнения функции
knapsack_s в программе используется стандартная функция
clock, возвращающая количество условных единиц времени,
прошедших с момента запуска программы. Разница между
возвращаемыми значениями функции clock, полученными до
вызова
knapsack_s
и
после,
позволяет
оценить
продолжительность выполнения этой функции.

32.

// Knapsack.h
#pragma once
#include "Combi.h"
int knapsack_s(
int V,
// [in] вместимость рюкзака
short n,
// [in] количество типов
предметов
const int v[], // [in] размер предмета
каждого типа
const int c[], // [in] стоимость предмета
каждого типа
short m[] // [out] количество предметов
каждого типа
);

33.

// Knapsack.cpp
#include "stdafx.h"
#include "Knapsack.h"
#define NINF 0x80000000 // самое малое int-число
int calcv(combi::subset s, const int v[]) // объем в рюкзаке
{
int rc = 0;
for (int i = 0; i < s.sn; i++) rc += v[s.ntx(i)];
return rc;
};
int calcc(combi::subset s, const int v[], const int c[])//стоимость в рюкзаке
{
int rc = 0;
for (int i = 0; i < s.sn; i++) rc += (v[s.ntx(i)]*c[s.ntx(i)]);
return rc;
};
void setm(combi::subset s, short m[]) //отметить выбранные предметы
{
for (int i = 0; i < s.n; i++) m[i] = 0;
for (int i = 0; i < s.sn; i++) m[s.ntx(i)] = 1;
};

34.

int knapsack_s(
int V,
// [in] вместимость рюкзака
short n,
// [in] количество типов предметов
const int v[], // [in] размер предмета каждого типа
const int c[], // [in] стоимость предмета каждого типа
short m[] // [out] количество предметов каждого типа {0,1}
)
{
combi::subset s(n);
int maxc = NINF, cc = 0;
short ns = s.getfirst();
while (ns >= 0)
{
if (calcv(s, v) <= V)
if ((cc = calcc(s,v,c)) > maxc)
{
maxc = cc;
setm(s,m);
}
ns = s.getnext();
};
return maxc;
};

35.

Генерация сочетаний
Булеан 2 X можно рассматривать как
объединение всевозможных
|X |
сочетаний, построенных из элементов множества X : 2 C X ,m . Поэтому
X
m 0
генерация множества C X , m может быть сведена к генерации булеана 2 X и
выбору из него всех подмножеств с мощностью m.
n!
C
(n m)!m!
m
n
m 3
C3, A C43
4!
4
(4 3)!3!

36.

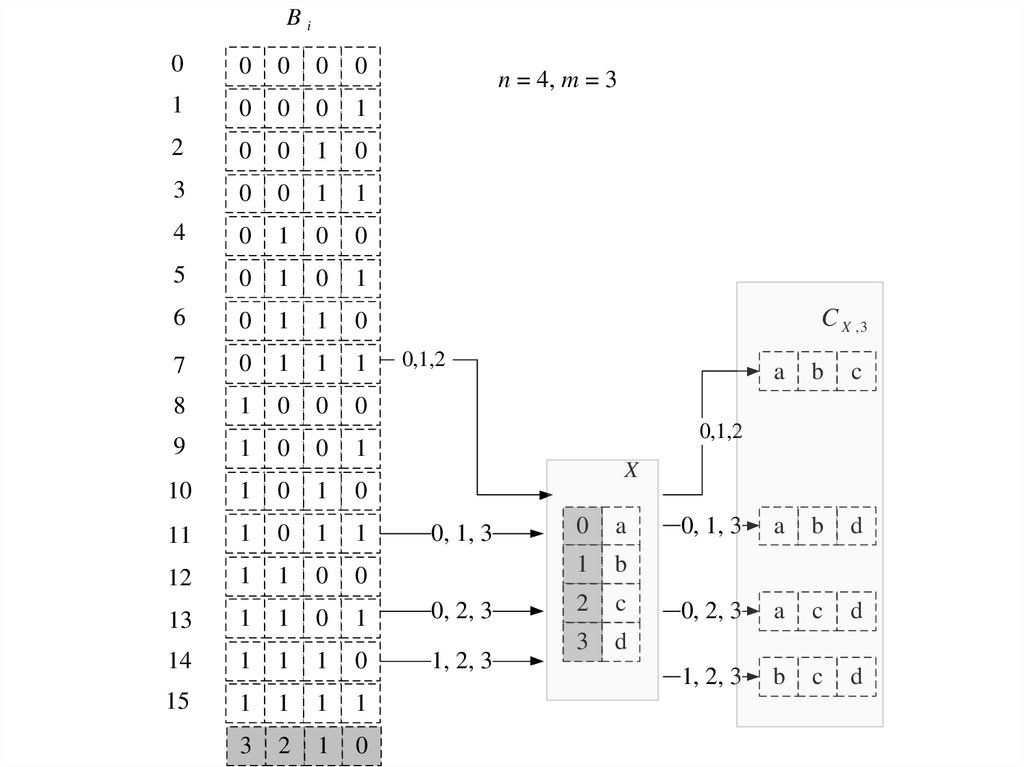
Генерация сочетаний
Схема построения множества сочетаний CX,3 из элементов
множества X={a, b, c, d} Закрашенным прямоугольником на
рисунке обозначены номера (индексы) элементов битовых
последовательностей Bi i 0, 15 и элементов множества X.
Стрелки связывают битовые последовательности, содержащие
три двоичные единицы и сгенерированные сочетания множества
CX,3 Для каждой стрелки указаны индексы единичных позиций
соответствующих битовых последовательностей. Эти индексы
используются для выбора элементов из множества X для
включения в соответствующее сочетание. Очевидно, что такой
алгоритм генерации сочетаний имеет сложность O(2|X | ), как и
алгоритм генерации множества всех подмножеств.

37.

Bi
0
0
0
0
0
1
0
0
0
1
2
0
0
1
0
3
0
0
1
1
4
0
1
0
0
5
0
1
0
1
6
0
1
1
0
7
0
1
1
1
8
1
0
0
0
9
1
0
0
1
n = 4, m = 3
C X ,3
0,1,2
a
b
c
0, 1, 3
a
b
d
0, 2, 3
a
c
d
1, 2, 3
b
c
d
0,1,2
X
10
1
0
1
0
11
1
0
1
1
12
1
1
0
0
13
1
1
0
1
0, 2, 3
14
1
1
1
0
1, 2, 3
15
1
1
1
1
3
2
1
0
0, 1, 3
0
a
1
b
2
c
3
d

38.

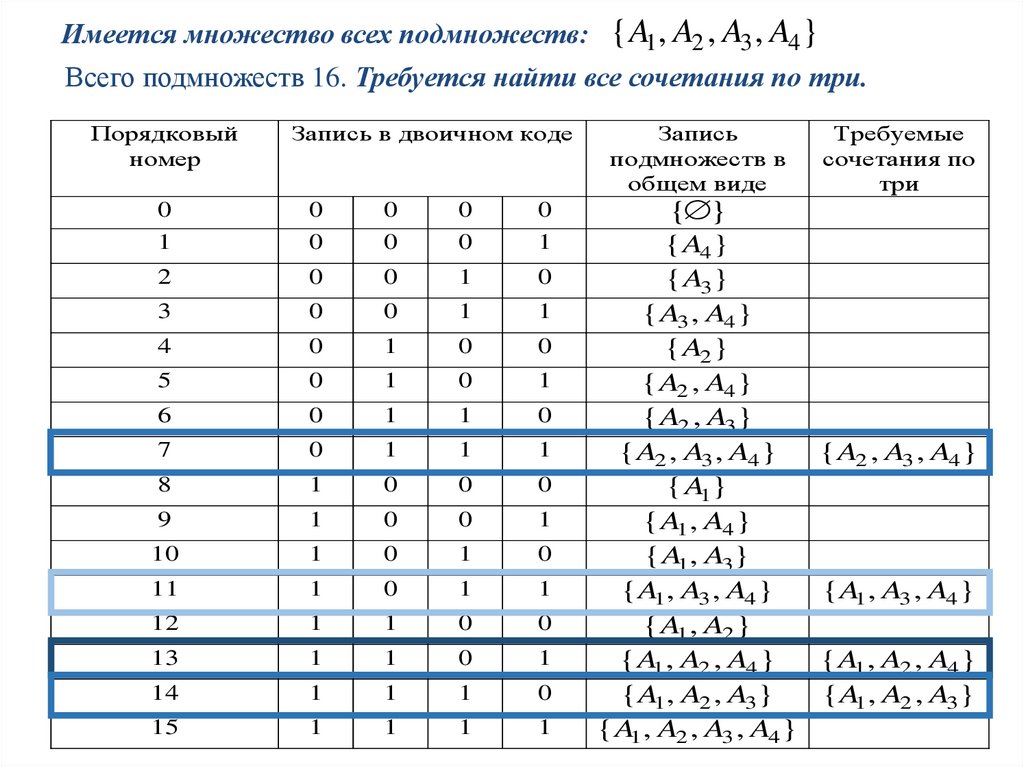
Имеется множество всех подмножеств: { A1 , A2 , A3 , A4 }
Всего подмножеств 16. Требуется найти все сочетания по три.
Порядковый
номер
Запись в двоичном коде
0
1
0
0
0
0
0
0
0
1
2
0
0
1
0
3
0
0
1
1
4
0
1
0
0
5
0
1
0
1
6
0
1
1
0
7
0
1
1
1
8
1
0
0
0
9
1
0
0
1
10
1
0
1
0
11
1
0
1
1
12
1
1
0
0
13
1
1
0
1
14
1
1
1
0
15
1
1
1
1
Запись
подмножеств в
общем виде
Требуемые
сочетания по
три
{ }
{ A4 }
{ A3}
{ A3 , A4 }
{ A2 }
{ A2 , A4 }
{ A2 , A3}
{ A2 , A3 , A4 }
{ A1}
{ A1 , A4 }
{ A1 , A3}
{ A1 , A3 , A4 }
{ A1 , A2 }
{ A1 , A2 , A4 }
{ A1 , A2 , A3}
{ A1 , A2 , A3 , A4 }
{ A2 , A3 , A4 }
{ A1 , A3 , A4 }
{ A1 , A2 , A4 }
{ A1 , A2 , A3}

39.

Реализация генератора сочетаний на языке С++.
Генератор реализован в виде структуры xcombination.
Структура xcombination имеет один конструктор с двумя
параметрами. Первый параметр определяет количество
элементов в исходном множестве, второй – количество
элементов в генерируемых сочетаниях.
Для хранения текущего состояния генератора используются
переменные: n (мощность исходного множества), m (количество
элементов в генерируемых сочетаниях), sset (адрес нулевого
элемента массива индексов) и nc (номер текущего сочетания).
Все переменные инициализируются в конструкторе. Значение nc
увеличивается на единицу после формирования очередного
сочетания, а значение остальных переменных остается
постоянным.
Кроме конструктора, структура xcombination содержит еще
пять функций.

40.

Реализация генератора сочетаний на языке С++.
Функция getfirst не имеет параметров и предназначена для
проверки корректности параметров, заданных в конструкторе. Эта
функция не формирует массива индексов, как это происходило в
структуре subset (генератор множества всех подмножеств). В
основном она существует для унификации интерфейсов всех
генераторов. Функция возвращает отрицательное значение, если
параметры генератора заданы неверно.
Функция getnext формирует массив индексов следующего
сочетания и увеличивает значение переменной nc на единицу. При
каждом вызове функции для текущего массива индексов вычисляется
новое значение j-индекса и, если оно не превышает m, строится
новый массив индексов. При достижении j-индексом значения,
равного или превышающего m, функция возвращает отрицательное
значение, в других случаях возвращается положительное значение.

41.

Реализация генератора сочетаний на языке С++.
Функция ntx возвращает значение элемента массива
индексов по индексу этого элемента и служит для
сокращения записи
при
переборе элементов
массива.
Функция count вычисляет и возвращает общее
количество сочетаний из n по m.
Как и в генераторе множества всех подмножеств, для
сброса генератора сочетаний в начальное состояние
служит функция reset. После вызова reset снова могут
вызываться getfirst и getnext.

42.

Реализация генератора сочетаний на языке С++.
В качестве исходного множества в примере используется
строковый массив, состоящий из пяти элементов. Вначале
программы этот массив распечатывается. Далее объявляется
структура xcombination и ее конструктору в качестве
параметров передаются количество элементов исходного
множества и размерность сочетаний.
Генерация сочетаний начинается функцией getfirst. Если
функция возвращает положительное значение, то сформирован
индекс массивов первого сочетания. Массив индексов каждого
следующего сочетания формируется функцией getnext. Выбор
элементов исходного массива осуществляется с помощью
функции ntx. Признаком завершения цикла генерации является
отрицательное значение функции getnext.

43.

// Combi.h
#pragma once
namespace combi
{
struct xcombination
// генератор сочетаний (эвристика)
{
short n,
// количество элементов исходного множества
m,
// количество элементов в сочетаниях
*sset;
// массив индексов текущего сочетания
xcombination (
short n = 1, //количество элементов исходного множества
short m = 1 // количество элементов в сочетаниях
);
void reset();
// сбросить генератор, начать сначала
short getfirst();
// сформировать первый массив индексов
short getnext();
// сформировать следующий массив индексов
short ntx(short i);
// получить i-й элемент массива индексов
unsigned __int64 nc;
// номер сочетания 0,..., count()-1
unsigned __int64 count() const; // вычислить количество сочетаний
};
};

44.

// Combi.cpp
#include "stdafx.h"
#include "Combi.h"
#include <algorithm>
namespace combi
{
xcombination::xcombination (short n, short m)
{
this->n = n;
this->m = m;
this->sset = new short[m+2];
this->reset();
}
void xcombination::reset() // сбросить генератор, начать сначала
{
this->nc = 0;
for(int i = 0; i < this->m; i++) this->sset[i] = i;
this->sset[m] = this->n;
this->sset[m+1] = 0;
};
short xcombination::getfirst()
{ return (this->n >= this->m)?this->m:-1; };

45.

short xcombination::getnext()//сформировать следующий массив индексов
{
short rc = getfirst();
if (rc > 0)
{
short j;
for (j = 0; this->sset[j]+1 == this->sset[j+1]; ++j)
this->sset[j] = j;
if (j >= this->m) rc = -1;
else {
this->sset[j]++;
this->nc++;
};
}
return rc;
};
short xcombination::ntx(short i)
{ return this->sset[i]; };
unsigned __int64 fact(unsigned __int64 x){ return (x == 0)?1:(x*fact(x-1));};
unsigned __int64 xcombination::count() const
{ return (this->n >= this->m)?
fact(this->n)/(fact(this->n-this->m)*fact(this->m)):0; };};

46.

Решение задачи об оптимальной загрузке судна на основе
генератора сочетаний
На палубе судна имеется m мест для размещения стандартных
контейнеров. Выбрать n контейнеров для погрузки на судно можно из n m
имеющихся в наличии. Каждый контейнер i характеризуется весом vi и
доходом ci , i 1, n от его перевозки. Необходимо выбрать m контейнеров
таким образом, чтобы их общий вес не превышал V , но при этом доход от
перевозки был максимально возможным.
Математическая модель задачи
m
m
ck max ,
vk V ,
i
k i {1, 2, ..., n},
(i j )
ki k j ,
i 1, m
i 1
i
i 1
Решением задачи будет вектор
(k1 , k 2 , ..., k m ).
Каждый элемент этого вектора может принимать целое значение
из отрезка [1, n], и при этом все значения ki должны быть
разными.

47.

Схема решения задачи с применением генератора подмножеств.
Задача имеет следующие исходные данные:
V=1000 – ограничение по общему весу контейнеров;
n=6 – количество контейнеров;
m=3 – количество свободных мест на палубе;
(100, 200, 300, 400, 500, 150) – вес контейнеров;
(10, 15, 20, 25, 30, 35) – доход от перевозки контейнеров.
Строки таблицы, озаглавленной символом CX,3 представляют
собой все сочетания по три из множества {0, 1, 2, 3, 4, 5}. Эти
сочетания могут быть получены с помощью соответствующего
генератора.
Несложно убедиться, что количество строк составляет C63 20,
а порядок их перечисления соответствует порядку генерации
сочетаний, рассмотренным выше алгоритмом.

48.

Схема решения задачи с применением
генератора подмножеств.
Используя элементы сгенерированных сочетаний в качестве
индексов для массивов vi , i 1, n (вес каждого контейнера) и
ci , i 1, n
(доход от перевозки), осуществляется выбор
соответствующих значений (вторая таблица слева) , что
позволяет рассчитать вес (столбец ∑vi) и доход от перевозки
(столбец ∑ci) комбинации контейнеров. Решением задачи
будет сочетание контейнеров, имеющее максимальный
суммарный доход при допустимом суммарном весе. Строка,
соответствующая решению, отмечена рамкой.

49.

C X ,3
0
0
1
2
1
0
1
3
2
0
2
3
3
1
2
3
4
0
1
4
5
0
2
4
6
1
2
4
7
0
3
4
8
1
3
4
9
2
3
4
10
0
1
5
11
0
2
5
12
1
2
5
13
0
3
5
14
1
3
5
15
2
3
5
16
0
4
5
17
1
4
5
18
2
4
5
19
3
4
5
vi
100 200 300 400 500 150
ci
10
V 1000
15
20
100 200 300
10 15 20
100 200
10 15
100
300
10
20
200 300
15 20
100 200
10 15
100
300
10
20
200 300
15 20
100
10
200
15
300
20
100 200
10 15
100
300
10
20
200 300
15 20
100
10
200
15
300
20
100
10
200
15
300
20
25
30
25
400
25
400
25
400
25
500
30
500
30
500
30
400 500
25 30
400 500
25 30
400 500
25 30
400
25
400
25
400
25
500
30
500
30
500
30
400 500
25 30
v
i
c
600
45
700
50
800
55
900
60
800
55
900
60
1000
65
1000
65
1100
1200
150
25
150
25
150
25
150
25
150
25
150
25
150
25
150
25
150
25
150
25
450
40
550
55
650
60
650
60
650
65
850
70
750
65
850
70
950
75
1050
i

50.

Пример реализации на языке С++ функции boat,
решающей задачу об оптимальной загрузке судна.
Функция
boat
имеет
пять
входных
параметров,
определяющих условие задачи: V (максимальный допустимый
суммарный вес контейнеров), m (количество мест на палубе
для установки контейнеров), n (общее количество
контейнеров), v (массив размерностью n, содержащий вес
каждого контейнера), c (массив размерностью n, содержащий
доход от перевозки каждого контейнера), а также один
возвращаемый параметр r (массив размерностью m,
содержащий номера выбранных контейнеров). В том случае,
если
решение существует, функция boat возвращает
положительное значение, иначе – нуль.

51.

Пример реализации на языке С++ функции boat, решающей
задачу об оптимальной загрузке судна.
В процессе своей работы функция boat использует генератор
сочетаний
(combi::xcombination)
и
вызывает
три
вспомогательные функции: boatfnc::calcv (расчет веса текущего
сочетания контейнеров), boatfnc::calcс (расчет дохода от
транспортировки
текущего
сочетания
контейнеров)
и
boatfnc::copycomb (копирование текущей комбинации).
Функция boat последовательно генерирует все возможные
сочетания по m контейнеров, вычисляет для каждого сочетания
суммарный вес (функция boatfnc::calcv), для сочетаний с весом,
не превышающим допустимое значение V, вычисляет доход от
перевозки этих контейнеров (boatfnc::calcс), фиксирует
оптимальную комбинацию контейнеров (boatfnc::copycomb) и
возвращает оптимальную доходность или нуль, если решения
нет.

52.

Предприятие может предоставить работу по
одной специальности 4 женщинами, по
другой - 6 мужчинам, по третьей - 3
работникам независимо от пола. Сколькими
способами можно заполнить вакантные
места, если имеются 14 претендентов: 6
женщин и 8 мужчин?

53.

Задача о предприятии
Имеем 14 претендентов и 13 рабочих мест. Сначала выберем работников на
первую специальность, то есть 4 женщин из 6:
6!
C
15
4! 2!
4
6
Далее независимо аналогичным образом выберем мужчин на вторую
специальность:
8!
C
28
6! 2!
6
8
Осталось 2 женщины, 2 мужчин и 3 вакантных места, которые, по условию, могут
занять любые из четырех оставшихся человек. Это может быть сделано 2
вариантами:
1
1. 1 женщина и 2 мужчин (выбираем женщину C2 2
способами)
2. 1 мужчина и 2 женщины (выбираем мужчину C21 2
способами).
В итого получаем 15 · 28(2 + 2) = 1680 способов.

54.

Сколько различных дробей
можно составить из чисел 3, 5,
7, 11, 13, 17 так, чтобы в
каждую дробь входили 2
различных числа? Сколько
среди них будет правильных
дробей?

55.

Задача о дробях
Различных дробей из 6 чисел: 3, 5, 7, 11, 13, 17 можно
составить
6!
C 2
2 30
4! 2!
2
6
C62 15
способами выбираем два числа из 6, и двумя
способами составляем из них дробь: сначала одно число –
числитель, другое знаменатель и наоборот).
Из этих 30 дробей ровно 15 будут правильные (т.е., когда
числитель меньше знаменателя):
способами выбираем два числа из 6, и единственным
C62 15
образом составляем дробь так, чтобы числитель был
меньше знаменателя.
ОТВЕТ. 30; 15.