Similar presentations:
Геометрия треугольника
1.
М ИН И С ТЕ РС ТВ О О Б РОЗО ВАН ИЯ И Н АУ К И А Л ТА ЙС КО ГОК РА Я
К РА Е В ОЕ ГО С УДА РСТВЕН Н ОЕ П РО ФЕССИ ОН АЛ ЬН ОЕ
О Б РА З О ВАТЕЛ ЬН ОЕ УЧ Е РЕ ЖДЕН И Е
" А Л ТА ЙС КИЙ А РХ ИТЕ КТ У РН О -С ТРО И ТЕЛ ЬН ЫЙ КОЛ Л ЕДЖ"
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ ПО
ТЕМЕ:
Геометрия треугольника
Шубин Д.Ю.
Барнаул 2024
Преподователь:Тарасова Татьтяна
Ивановна
2.
СодержаниеВведение……………………………………………………………………….….3
1. Треугольник как символ. Исторические сведения. …......………….......3
2. Треугольник в геометрии. ……………………………….…………………..4
2.1. Понятие……………………................................................…………………..4
2.1.1. Основные элементы треугольника ABC.......................................................5
СОДЕРЖАНИЕ
2.1.2. Виды треугольников.......................................................................................5
2.1.3 Треугольник Рело.............................................................................................6
2.1.4. Замечательные точки треугольника...............................................................8
3. Треугольники вокруг нас.....................……………………………………..12
3.1. Треугольник в математике.............................................................................14
3.2. Треугольник в астрономии.............................................................................15
3.3. Треугольник в музыке....................................................................................15
4.Заключение……………………………………………………………………...16
Используемые источники……..……………………………………………17
3.
ЦЕЛЬ И ЗАДАЧИОбобщение знаний о треугольниках, и их практическом применении.
Изучение исторических сведений о треугольниках;
Изучение сведений о нахождении треугольников в окружающем мире;
Исследование свойств треугольников и применения этих свойств в решении
практических задач.
Практическая значимость: данный материал способствует формированию
представления о прикладных возможностях математики.
4.
РАЗДЕЛ I.ТРЕУГОЛЬНИК КАК СИМВОЛ.
ИСТОРИЧЕСКИЕ СВЕДЕНИЯ.
Треугольник является одной из первых
геометрических фигур, которая стала
использоваться в орнаментах древних народов.
Треугольник был одной из первых
геометрических фигур, используемых в
орнаментах древних цивилизаций. В различных
культурах он символизировал различные
концепции и ценности. Например, в Древнем
Египте треугольник имел прямоугольную форму
и представлял триаду духовной воли, любви и
разума.
5.
РАЗДЕЛ II. ТРЕУГОЛЬНИК ВГЕОМЕТРИИ.
П.2.1 ПОНЯТИЕ.
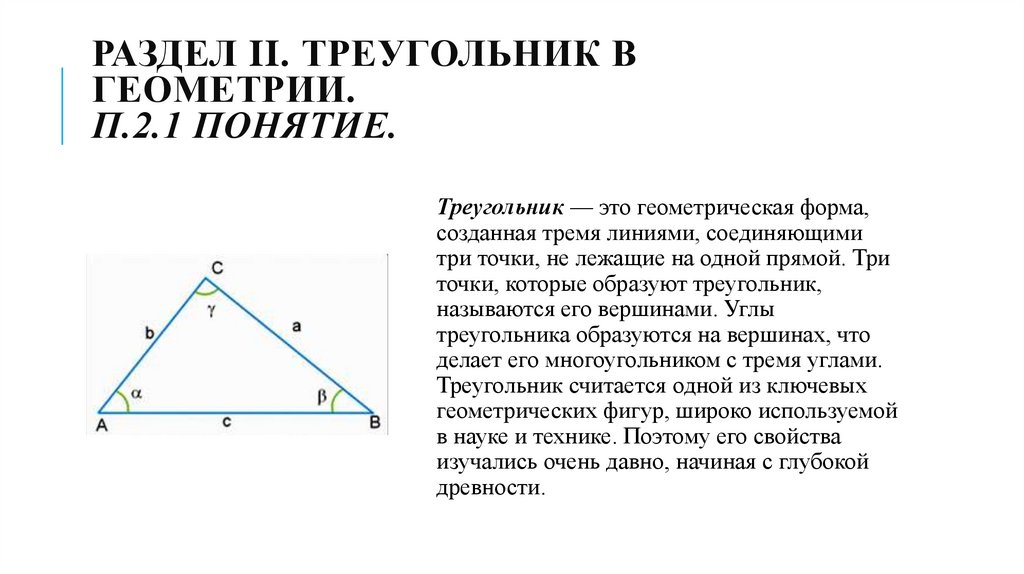
Треугольник — это геометрическая форма,
созданная тремя линиями, соединяющими
три точки, не лежащие на одной прямой. Три
точки, которые образуют треугольник,
называются его вершинами. Углы
треугольника образуются на вершинах, что
делает его многоугольником с тремя углами.
Треугольник считается одной из ключевых
геометрических фигур, широко используемой
в науке и технике. Поэтому его свойства
изучались очень давно, начиная с глубокой
древности.
6.
2.1.1. ОСНОВНЫЕ ЭЛЕМЕНТЫТРЕУГОЛЬНИКА ABC
Вершины – точки A, B, и C;
Стороны – отрезки a = BC, b = AC и c = AB, соединяющие вершины;
Углы – α, β, γ образованные тремя парами сторон. Углы часто обозначают так
же, как и вершины, – буквами A, B и C.
Угол, образованный сторонами треугольника и лежащий в его внутренней
области, называется внутренним углом, а смежный к нему является внешним
углом треугольника.
7.
2.1.2. ВИДЫТРЕУГОЛЬНИКОВ.
Треугольник, все стороны которого равны, называется равносторонним.
Треугольник называется равнобедренным, если у него две стороны равны.
Треугольник называется остроугольным, если все его углы острые.
Треугольник называется тупоугольным, если один из его углов тупой.
Треугольник называется прямоугольным, если у него есть прямой угол, то
есть угол в 90°.
Египетский треугольник –прямоугольный треугольник с соотношением
сторон 3:4:5. Особенностью треугольника, известной ещё со времён
античности, является то, что при таком отношении сторон теорема
Пифагора даёт целые квадраты как катетов, так и гипотенузы, то есть
9:16:25.
8.
ИСТОРИЯТРЕУГОЛЬНИКА
Эллины назвали треугольник с определенным
отношением сторон. В VII-V веках до н. э.
греческие философы и общественные деятели
посещали Египет, где, например, Пифагор
учился астрономии и математике под
руководством Фалеса. Возможно, именно
изучение отношений сторон египетского
треугольника побудило Пифагора
сформулировать и доказать свою знаменитую
теорему.
9.
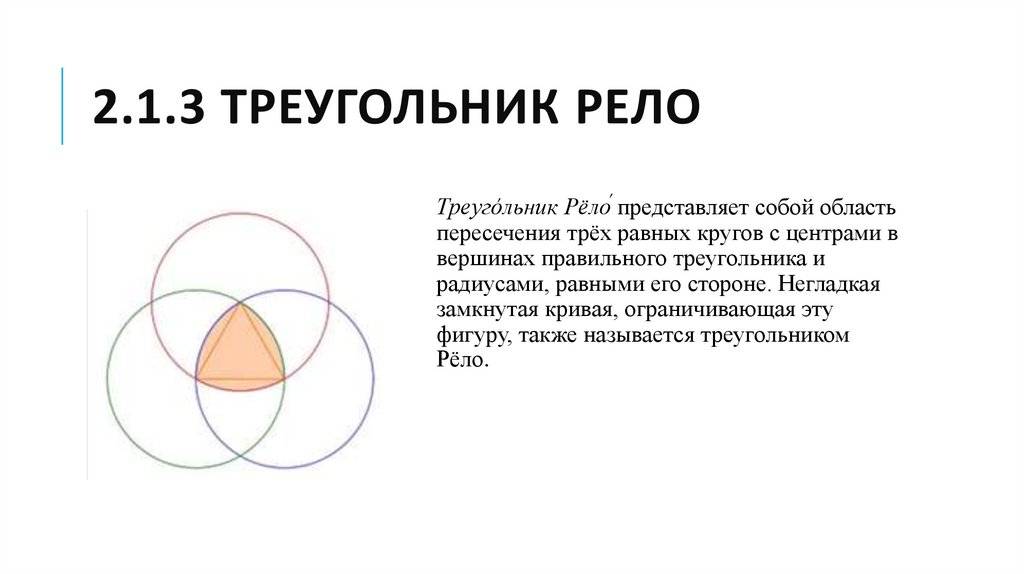
2.1.3 ТРЕУГОЛЬНИК РЕЛОТреуго́льник Рёло́ представляет собой область
пересечения трёх равных кругов с центрами в
вершинах правильного треугольника и
радиусами, равными его стороне. Негладкая
замкнутая кривая, ограничивающая эту
фигуру, также называется треугольником
Рёло.
10.
Неравенство треугольникаВ треугольнике сумма длин двух его сторон больше
длины третьей стороны.
Дополнительное свойство: каждая сторона
треугольника больше разности двух других сторон.
РЕЛО
Теорема о сумме углов треугольник
Сумма внутренних углов треугольника всегда равна
180°:
α + β + γ = 1800.
В геометрии Лобачевского сумма углов треугольника
всегда меньше 180°, а на сфере — всегда больше.
11.
2.1.4. ЗАМЕЧАТЕЛЬНЫЕТОЧКИ ТРЕУГОЛЬНИКА
Обычно они расположены внутри
треугольника, но и это не
обязательно. В частности, точка
пересечения высот может находиться
вне треугольника.
Замечательными точками
треугольника являются точки
пересечения:
12.
СВОЙСТВА:ЦЕНТР ВПИСАННОЙ ОКРУЖНОСТИ ТРЕУГОЛЬНИКА НАХОДИТСЯ НА ОДИНАКОВОМ
РАССТОЯНИИ ОТ ВСЕХ СТОРОН ТРЕУГОЛЬНИКА.
B + C A {\DISPLAYSTYLE {\FRAC {B+C}{A}}} 3. ВЫСОТ — ОРТОЦЕНТР :
В ЗАВИСИМОСТИ ОТ ВИДА ТРЕУГОЛЬНИКА ОРТОЦЕНТР МОЖЕТ НАХОДИТЬСЯ ВН УТРИ
ТРЕУГОЛЬНИКА (В ОСТРОУГОЛЬНОМ), ВНЕ ЕГО (В ТУПОУГОЛЬНОМ) ИЛИ СОВ ПАДАТЬ
С ВЕРШИНОЙ (В ПРЯМОУГОЛЬНОМ — СОВПАДАЕТ С ВЕРШИНОЙ ПРИ ПРЯМОМ УГЛЕ)
Если в четвёрке точек A {\displaystyle A}А, B
{\displaystyle B}В, C {\displaystyle C}С, D
{\displaystyle D} D точка D {\displaystyle D} D
является точкой пересечения высот треугольника
A B C {\displaystyle ABC}ABC, то и любая из
четырёх точек является ортоцентром
треугольника, образованного тремя остальными
точками. Такую четвёрку иногда называют
ортоцентрической системой точек.
13.
РАЗДЕЛ III . ТРЕУГОЛЬНИКИВОКРУГ НАС.
Изображения треугольников и задачи на треугольники встречаются во многих папирусах Древней
Греции и Древнего Египта. Еще в древности стали вводить некоторые знаки обозначения для
геометрических фигур.
Древнегреческий ученый Герон (I век) впервые применил знак вместо слова треугольник.
Треугольник - это одна из первых геометрических фигур, которая нашла широкое применение в
орнаментах древних обществ. Различные типы жилищ, такие как вигвамы, юрты и палатки, обладают
конусообразной формой, поэтому в сечении они образуют треугольник. Это помогает им легко
справляться с ветрами и эффективно сливать воду. Крыши старых деревянных домов и современных
зданий имеют также форму треугольника, чтобы растаявший снег и дождевая вода могли стекать
быстро и эффективно. Треугольная форма встречается и в предметах одежды человека. Головные
уборы различных культур, такие как треуголки, пилотки, колпаки и косынки, обычно имеют
треугольную форму. Женские платки перед накидыванием на голову также складываются пополам.
При пошиве юбок часто используют клинья, имеющие форму треугольника, чтобы добавить
пышности. Одежду хранят на плечиках с треугольной формой, чтобы избежать помятости.
14.
ШИРОКОЕ ПРИМЕНЕНИЕ В ЖИЗНИЧЕЛОВЕКА НАШЛО СВОЙСТВО
ЖЕСТКОСТИ ТРЕУГОЛЬНИКА.
СИМВОЛ ФРАНЦИИ ЗНАМЕНИТАЯ
ЭЙФЕЛЕВА БАШНЯ - САМАЯ
УЗНАВАЕМАЯ АРХИТЕКТУРНАЯ
ДОСТОПРИМЕЧАТЕЛЬНОСТЬ
ПАРИЖА. КОЛЕБАНИЯ БАШНИ ВО
ВРЕМЯ БУРЬ НЕ ПРЕВЫШАЮТ 15
СМ. ЭТО ОБЪЯСНЯЕТСЯ ТЕМ, ЧТО
ВСЯ КОНСТРУКЦИЯ БАШНИ
СПЛЕТЕНА ИЗ ТРЕУГОЛЬНИКОВ,
ОБЛАДАЮЩИХ ЖЁСТКОСТЬЮ.
ВО ВРЕМЯ ВЕЛИКОЙ
ОТЕЧЕСТВЕННОЙ ВОЙНЫ ДЛЯ
СОХРАНЕНИЯ СТЕКОЛ ВО ВРЕМЯ
БОМБЕЖКИ ИХ ЗАКЛЕИВАЛИ
БУМАЖНЫМИ ПОЛОСКАМИ,
ЧТОБЫ ПОЛУЧИЛСЯ
ТРЕУГОЛЬНИК.
В ОСНОВЕ ГЕОДЕЗИЧЕСКОГО
КУПОЛА ЛЕЖИТ КАРКАС,
ПРЕДСТАВЛЯЮЩИЙ СОБОЙ
ПРОСТРАНСТВЕННУЮ ФЕРМУ В
ВИДЕ ПОЛУСФЕРЫ. ИМЕННО ИЗ
ТРЕУГОЛЬНИКОВ И СОСТОИТ
ОСНОВНОЙ КАРКАС ГЕОКУПОЛА.
БЛАГОДАРЯ СВОЕЙ КОНСТРУКЦИИ
ГЕОДЕЗИЧЕСКИЕ КУПОЛА
ВЫДЕРЖИВАЮТ НАГРУЗКИ, В
НЕСКОЛЬКО РАЗ ПРЕВЫШАЮЩИЕ
ДОПУСТИМЫЕ НАГРУЗКИ ДЛЯ
ОБЫЧНЫХ ПРЯМОУГОЛЬНЫХ
СООРУЖЕНИЙ.
Во время Великой Отечественной войны для
сохранения стекол во время бомбежки их заклеивали
бумажными полосками, чтобы получился треугольник.
В основе геодезического купола лежит каркас,
представляющий собой пространственную ферму в
виде полусферы. Именно из треугольников и состоит
основной каркас геокупола. Благодаря своей
конструкции геодезические купола выдерживают
нагрузки, в несколько раз превышающие допустимые
нагрузки для обычных прямоугольных сооружений.
Так, чтобы закрепить столб в вертикальном положении,
к нему ставят подпорку. Телеграфные столбы с
подпоркой называют анкерными.
Стропила зданий имеют вид треугольников. Это
придаёт им крепость и устойчивость.
15.
П.3.1. ТРЕУГОЛЬНИКВ МАТЕМАТИКЕ.
Треугольник Паскаля - это бесконечная таблица биномиальных
коэффициентов, которая имеет треугольную форму и названа в честь
французского математика и философа Блеза Паскаля. В этом треугольнике на
вершине и по бокам располагаются единицы. Каждое число в треугольнике
равно сумме двух чисел, расположенных над ним. Строки треугольника
Паскаля симметричны относительно вертикальной оси.
16.
ТРЕУГОЛЬНИК СЕРПИНСОКГОВажным свойством треугольника Серпинского является его самоподобие ведь он состоит из трёх своих копий, уменьшенных в два раза (это части
треугольника Серпинского, содержащиеся в маленьких треугольниках,
примыкающих к углам).
Если в треугольнике Паскаля все нечётные числа окрасить в чёрный цвет, а
чётные — в белый, то образуется треугольник Серпинского.
17.
П.3.2. ТРЕУГОЛЬНИКВ АСТРОНОМИИ.
Треуго́льник (лат. Triangulum, Tri) — созвездие северного полушария неба.
Занимает на небе площадь 131,8 квадратных градуса, содержит 25 звёзд,
видимых невооружённым глазом.
В галактике Треугольника, или M33, которая расположена в созвездии
Треугольника, находится третья по величине в Местной группе галактика.
Звезды в этом созвездии не очень яркие, например, α является лишь третьей по
яркости звездой. В Треугольнике можно обнаружить всего 15 звезд. С
помощью телескопа можно увидеть двойную звезду ι, компоненты которой
окрашены в золотисто-жёлтый и зелено-голубой цвета.
18.
п.3.3. Треугольник в музыке.П.3.3.
ТРЕУГОЛЬНИК
В МУЗЫКЕ.
Треугольник - это ударный музыкальный
инструмент, который представляет собой
металлический прут, изогнутый в форме
треугольника. Один из углов остается открытым, а
концы прута обычно почти касаются друг друга.
Этот инструмент относится к категории
инструментов с неопределенной высотой звука и
имеет блестящий и яркий тембр, который может
украсить даже мощное оркестровое исполнение
tutti.
19.
РАЗДЕЛ IV .ЗАКЛЮЧЕНИЕ
Треугольники присутствуют повсюду в нашей жизни: в детских
игрушках, архитектурных сооружениях, дорожных знаках и
музыкальных инструментах. Часто мы перестаем обращать на
них внимание в повседневной жизни, но знание истории таких
обычных объектов может быть увлекательным и интересным.
С одной стороны, треугольники имеют богатую историю, а с
другой стороны, они представляют собой современный раздел
математики. Теория треугольников играет важную роль не
только в теоретических исследованиях по геометрии, но и в
других областях науки. Фраза великого французского
архитектора Ле Корбюзье, высказанная в начале ХХ века, что
«всё вокруг – геометрия», отлично отражает современный
период, в котором мы живем, насыщенный геометрическими
аспектами.
20.
СПИСОК ИСПОЛЬЗОВАННОЙЛИТЕРАТУРЫ
Атанасян Л. С. Геометрия: Учеб. для общеобразоват. учреждений. –
М.: Просвещение, 2002.
За страницами учебника алгебры: Кн. для учащихся 7 – 9 кл. сред. Шк. - М.:
Просвещение, 1990. – 224 с.: ил.
Мякишев А. Г., Элементы геометрии треугольника., Москва, МЦНМО, 2002.
Абачиев С. К. О треугольнике Паскаля, простых делителях и фрактальных
структурах // В мире науки, 1989, № 9.

















 mathematics
mathematics








