Similar presentations:
Арифметическая прогрессия
1.
24.02.22Классная работа
2.
Арифметическая прогрессия – это числоваяпоследовательность, каждый член которой,
начиная со второго равен предыдущему
сложенному с одним и тем же числом.
a1 , a2 , a3 ,..., an ... - арифметическая
прогрессия, если для всех натуральных n
выполняется равенство
an 1 an d
разность арифметической прогрессии
d -(число)
3.
Формула n-го членаарифметической прогрессии
an a1 (n 1) d
4.
Последовательности заданы несколькимипервыми членами. Одна уз них –
арифметическая прогрессия. Укажите ее.
А) 1; 4; 9; 16; …
Б) -3; -6; -9; -12; …
В) 1; 3; 9; 27; …
5.
Выписано несколько последовательныхчленов арифметической прогрессии:
…; 11; x; –13; –25; … .
Найдите член прогрессии, обозначенный
буквой .
6.
Свойство n –го членаарифметической прогрессии
an 1 an 1
an
2
7.
8.
24.02.22Классная работа.
• Сумма n-первых членов
арифметической прогрессии
9.
Цель урока:• Вывести формулу суммы n-членов
арифметической прогрессии,
выработать навыки
непосредственного применения
данной формулы
10.
11.
12.
Как Гауссу удалосьтак быстро
сосчитать сумму
такого большого
количества чисел?
13.
Рассмотрим в общем виде:аn – арифметическая прогрессия.
Sn = a1 + a2 + a3 + a4 + … + an-1 + an,
Sn = an + an-1 +an-2 + an-3 + … =a2 + a1
a2 + an-1 = (a1 + d) + (an – d) = a1 + an,
a3 + an-2 = (a2 + d) + (an-1 – d) = a2 + an-1 = a1 + an,
a4 + an-3 = (a3 + d) + (an-2 – d) = a3 + an-2 = a1 + an и
т.д.
2Sn = (a1 + an)n.
Sn = (a1 + an)n : 2 – формула суммы n первых
членов арифметической прогрессии.
14.
Сумма n первых членоварифметической прогрессии
a1 an
Sn
n
2
15.
16.
17.
18.
Задачи из ОГЭ• В первом ряду кинозала 50 мест, а в каждом
следующем на 1 больше, чем в
предыдущем. Сколько мест в зале на семи
рядах?
19.
Фигура составлена из квадратов так, какпоказано на рисунке. В каждом следующем
ряду на 2 квадрата больше, чем в
предыдущем. Сколько квадратов в 15-м ряду?
А) 35
Б) 33
В) 31
Г) 15
20.
1 вариант1. Последовательность (yn)
задана формулой уn = n2 –
4n. Найдите шестой член
этой последовательности.
2. Арифметическая
прогрессия (xn), x1=-3 и d=5.
Найдите пятый член этой
прогрессии.
.3.Найдите сумму восьми
первых членов
арифметической прогрессии,
если а1 =2, d= 6
2 вариант
1. . Последовательность
(аn) задана формулой аn = 2n
- n2. Найдите пятый член
этой последовательности
2. Арифметическая
прогрессия (xn), x1=5 и d=-5.
Найдите пятый член этой
прогрессии
3. Найдите сумму первых 12
членов арифметической
прогрессии (аn), если а1 =3,
d = 2.
21.
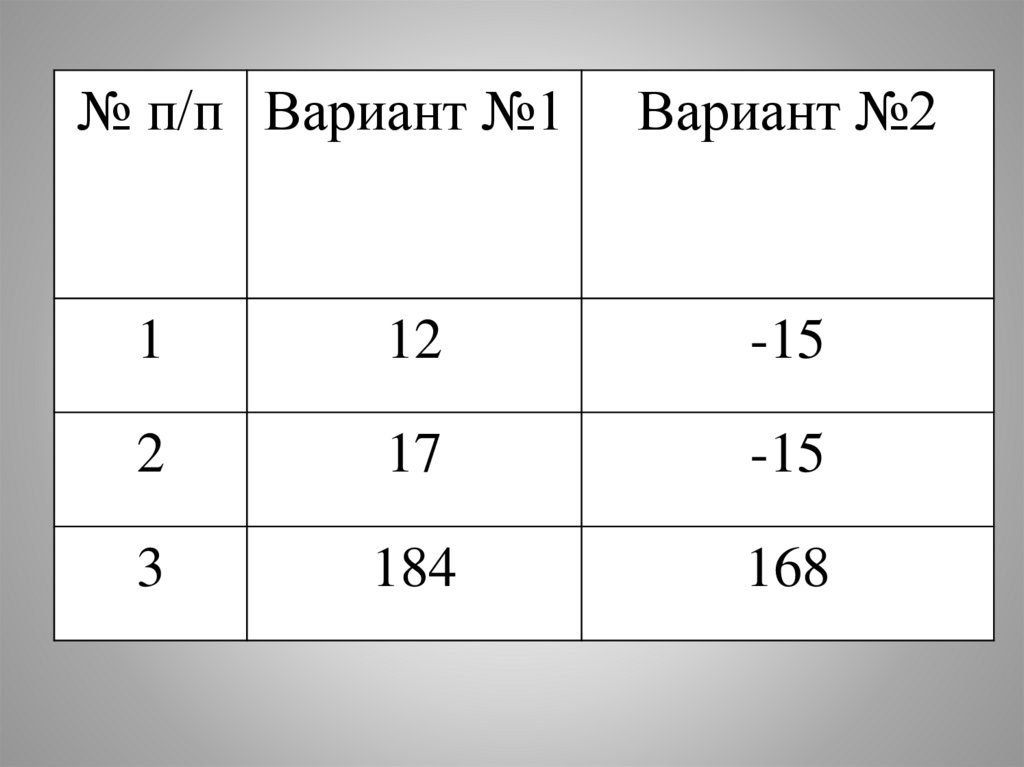
№ п/п Вариант №1Вариант №2
1
12
-15
2
17
-15
3
184
168
22.
Подведем итоги урокаПродолжите высказывание об уроке.
Я работал(а) на уроке на оценку …
На уроке я научился(ась) ..
Я думаю, домашнее задание для меня будет:
а) лёгким/трудным;






















 mathematics
mathematics








