Теорема Безу и следствие из неё. Урок алгебры в 11 классе

1.

Муниципальное бюджетное общеобразовательное
учреждение гимназия № 19 им.Н.З.Поповичевой
г.Липецка
Урок алгебры в 11 классе по теме:
«Теорема Безу и следствие из неё»
Автор: Маликова О.Г.,
учитель математики

2.

Метод решения хорош, если с самого
начала мы можем предвидеть - и далее
подтвердить это, - что, следуя этому
методу, мы достигнем цели.
(Г. Лейбниц)
Го́тфрид Ви́льгельм
Ле́йбниц (1646 - 1716) —
немецкий философ,
логик, математик

3.

Джерола́мо Карда́но
(1501-1576) —
итальянский математик
Ал-Хорезми
(ок. 783 — ок. 850) основатель
классической алгебры.
Лодовико Феррари
(1522-1565 ) —
итальянский математик,
нашедший общее решение
уравнения четвёртой
степени.

4.

Нильс Хенрик Абель (1802-1829)– норвежский
математик
В 1826 году норвежский
математик Абель доказал, что
нельзя вывести формулы для
решения уравнений пятой
степени и выше.

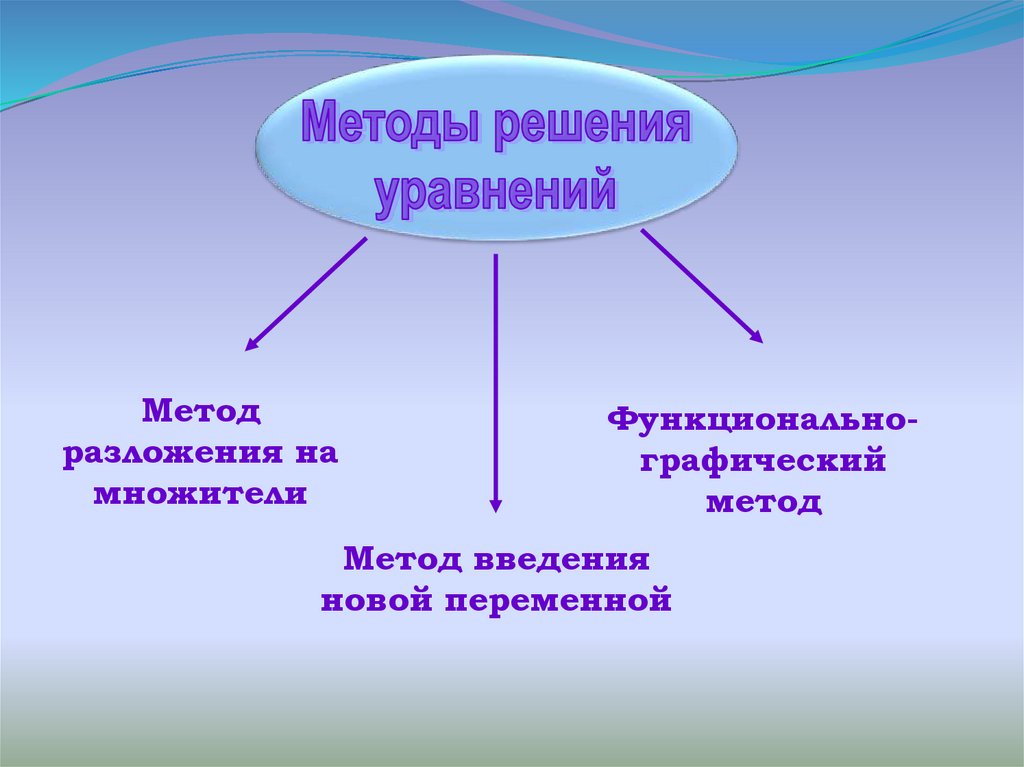
5.

Метод
разложения на
множители
Функциональнографический
метод
Метод введения
новой переменной

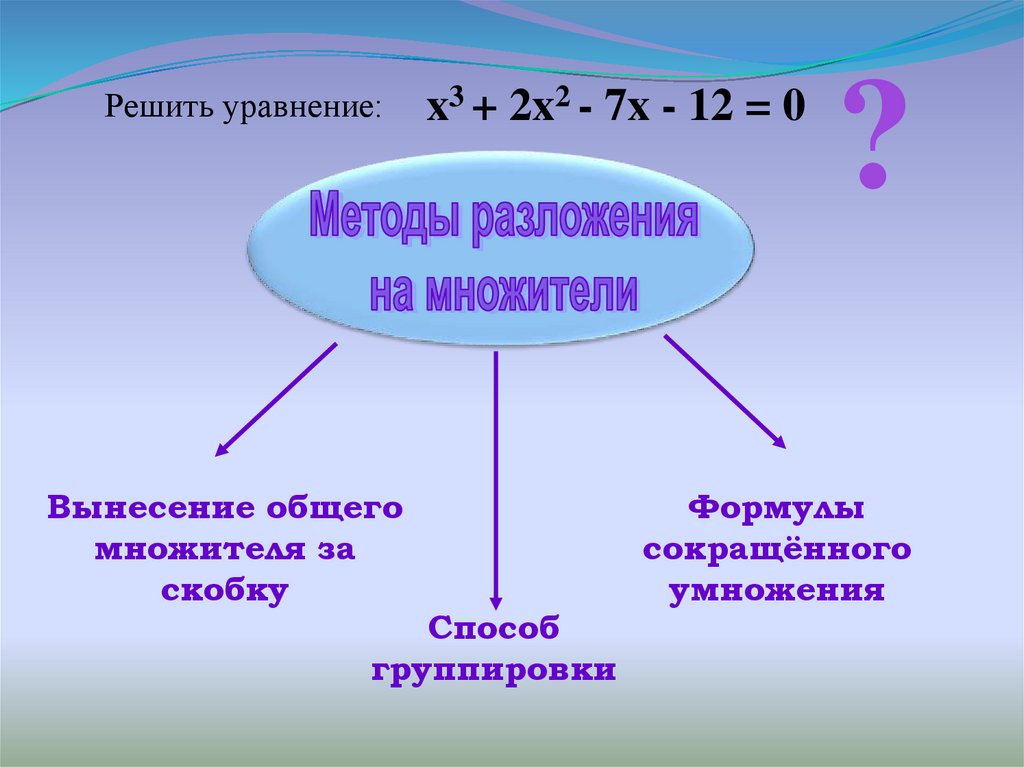
6.

Решить уравнение:
Вынесение общего
множителя за
скобку
x3 + 2x2 - 7x - 12 = 0
Способ
группировки
?
Формулы
сокращённого
умножения

7.

Решить уравнение:
x3 + 2x2 - 7x - 12 = 0
ах2 + bх + с = а(х – х1)(х – х2),
где х1 и х2 корни многочлена
?
Р(х) = x3 + 2x2 - 7x – 12
Делители свободного члена: ± 1; ± 2; ± 3; ± 4; ± 6; ± 12
х = - 3 - корень многочлена Р(х)
-3
1
1
2
-1
-7
-4
-12
0

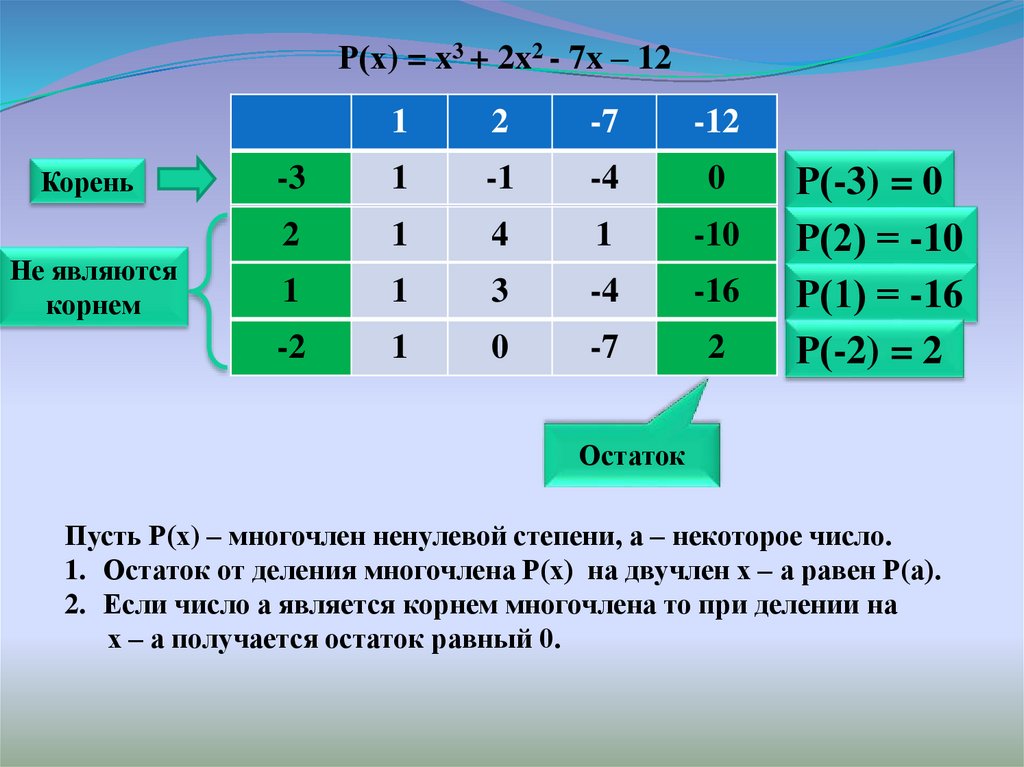
8.

Р(х) = x3 + 2x2 - 7x – 12
Корень
Не являются
корнем
1
2
-7
-12
-3
1
-1
-4
0
2
1
4
1
-10
1
1
3
-4
-16
-2
1
0
-7
2
Р(-3) = 0
Р(2) = -10
Р(1) = -16
Р(-2) = 2
Остаток
Пусть Р(х) – многочлен ненулевой степени, а – некоторое число.
1. Остаток от деления многочлена Р(х) на двучлен х – а равен Р(а).
2. Если число а является корнем многочлена то при делении на
х – а получается остаток равный 0.

9.

1. Остаток от деления многочлена Р(х) на двучлен х – а равен Р(а).
2. Если число а является корнем многочлена Р(х), то Р(х) делится на
двучлен х - а.
Доказательство:
1. По теореме о делении с остатком следует, что Р(х) = (х – а) Q(х) + r,
где Q(х) – многочлен степени на 1 меньше, чем р(х), r – остаток (число).
Пусть х = а, тогда Р(а) = (а – а)Q(х) + r = r. Ч.т.д.
Теорема Безу.
Остаток от деления многочлена Р(х) ненулевой
степени на двучлен х – а равен Р(а).
Доказательство:
2. Если число а – является корнем многочлена, то Р(а) = 0,
следовательно r = 0 и многочлен примет вид
Р(х) = (х – а) Q(х). Значит многочлен Р(х) делится на х – а.
Ч.т.д.
Этье́нн Безу́ (1730 - 1783)
Следствие из теоремы Безу
— французский
математик, член
Если число а является корнем многочлена
Парижской академии
Р(х), то Р(х) делится на двучлен х – а.
наук

10.

Решить уравнение:
x3 + 2x2 - 7x - 12 = 0
ах2 + bх + с = а(х – х1)(х – х2),
где х1 и х2 корни многочлена
?
Р(х) = x3 + 2x2 - 7x – 12
Делители свободного члена: ± 1; ± 2; ± 3; ± 4; ± 6; ± 12
х = -3 – корень многочлена Р(х)
-3
1
1
2
-1
-7
-4
x3 + 2x2 - 7x – 12 = 0
(х + 3)(x2 - х - 4) = 0
Ответ: -3;
-12
0

11.

Алгоритм решения уравнения с помощью
теоремы Безу
- найти все целые делители свободного члена;
- из этих делителей найти хотя бы один
корень уравнения;
- левую часть уравнения разделить на (x - a);
- записать в левой части уравнения
произведение делителя и частного;
- решить полученное уравнение.

12.

Подумай и реши:
1. Найдите остаток от деления многочлена
x3 - 3x2 + 6x – 5 на двучлен x - 2.
Решение: r = Р(2) = 3
2. При каком значении a многочлен
x4 + ax3 + 3x2 – 4x – 4 делится без остатка
на двучлен x – 2 ?
Решение: r = Р(2) = 8а + 16
8а + 16 = 0, а = -2
3. Разложите на множители х4 + 324?

13.

Дома: Докажите утверждение
«Многочлен степени n имеет не более n корней».

14.

Список использованной литературы
1.
А.Г.Мордкович, П.В.Семёнов. Алгебра и начала математического
анализа (профильный уровень), 11 класс. Ч. 1 – М: Мнемозина
Использованные Интернет-ресурсы
1. http://ru.wikipedia.org
2. http://www.ref.by/refs/49/32199/1.html