Элементы комбинаторики. 10 класс

1.

Элементы комбинаторики
10 класс 01марта
1

2.

Основные вопросы:
I. Что такое комбинаторика?
Какие задачи считают комбинаторными?
II. Перестановки
III. Размещения
IV. Сочетания
2

3.

Не будем спорить - будем
вычислять.
Г. Л е й б н и ц
• Комбинаторика – радел математики,
в котором рассматриваются задачи о
подсчёте числа комбинаций
составленных по определённым
правилам.
3

4.

II. Какие задачи считают комбинаторными?
Комбинаторные задачи
Задачи подсчёта числа комбинаций из конечного
числа элементов
• Комбинаторика – от латинского слова combinare,
что означает «соединять, сочетать».
• Методы комбинаторики находят широкое
применение в физике, химии, биологии,
экономики и др. областях знания.
Комбинаторику можно рассматривать как
часть теории множеств – любую комбинаторную
задачу можно свести к задаче о конечных
множествах и их отображениях.
4

5.

I. Уровни решения комбинаторных задач
1. Начальный уровень.
Задачи поиска хотя бы одного решения, хотя бы одного
расположения объектов, обладающих заданным
свойствами
- отыскание такого расположения десяти точек на пяти
отрезках, при котором на каждом отрезке лежит по
четыре точки;
- такого расположения восьми ферзей на шахматной доске,
при котором они не бьют друг друга.
Иногда удаётся доказать, что данная задача не имеет
решения
(например, нельзя расположить 10 шаров в 9 урнах так, что
бы в каждой урне было не более одного шара – хотя бы в
одной урне окажется не менее двух шаров).
5

6.

2. Второй уровень.
Если комбинаторная задача имеет несколько решений, то
возникает вопрос о подсчете числа таких решений,
описании всех решений данной задачи.
• 3. Третий уровень.
Решения данной комбинаторной задачи отличаются друг от
друга некоторыми параметрами. В этом случае возникает
вопрос отыскания оптимального варианта решения такой
задачи.
Например:
Путешественник хочет выехать из города А, посетить
города В, С, и D. После чего вернуться в город А.
6

7.

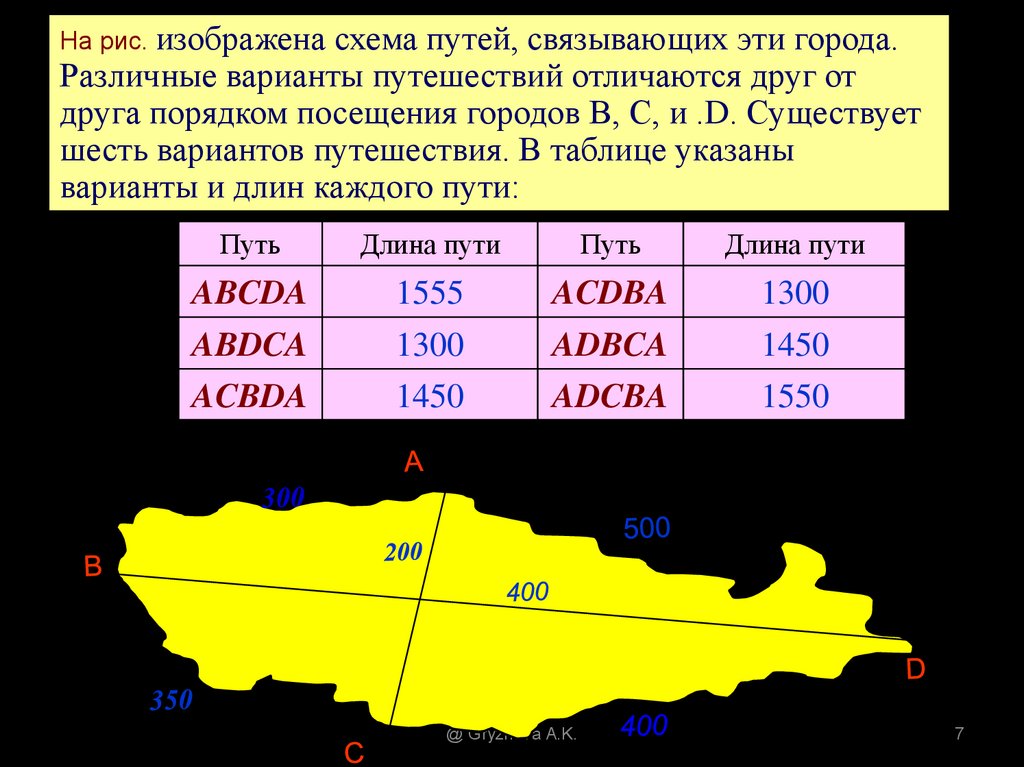
На рис. изображена схема путей, связывающих эти города.
Различные варианты путешествий отличаются друг от
друга порядком посещения городов В, С, и .D. Существует
шесть вариантов путешествия. В таблице указаны
варианты и длин каждого пути:
Путь
Длина пути
Путь
Длина пути
ABCDA
1555
ACDBA
1300
ABDCA
1300
ADBCA
1450
ACBDA
1450
ADCBA
1550
@ Gryznova A.K.
7

8.

• Комбинаторные задачи на
оптимизацию приходится решать
мастеру, стремящемуся к
быстрейшему выполнению задания,
агроному, стремящемуся к
наивысшей урожайности на данных
полях, и т.д.
8

9.

• Мы будем рассматривать лишь задачи
о подсчёте числа решений
комбинаторной задачи.
Этот раздел комбинаторики,
называемый теорией перечислений,
тесно связан с теорией вероятностей.
9

10.

Правила суммы и произведения
• 1. Сколько различных коктейлей можно составить из
четырёх напитков, смешивая их в равных количествах по
два?
В AB, AC, AD, BC, BD, CD – всего 6 коктейлей
• А
D
С
• 2. Сколько различных двузначных чисел можно составить из
цифр 0, 1, 2, 3 ?
Первой цифрой двузначного числа может одна из цифр 1, 2, 3 (цифра 0 не
может быть первой). Если первая цифра выбрана, то вторая может быть любая из
цифр 0, 1, 2, 3. Т.к. каждой выбранной первой соответствует четыре способа
выбора второй, то всего имеется
4 + 4 + 4 = 4·3 = 12
различных двузначных чисел.
10

11.

2. Сколько различных двузначных чисел можно составить из цифр
4 + 4 + 4 = 4·3 = 12 различных двузначных чисел.
Первая цифра
1
2
3
0, 1, 2, 3 ?
вторая цифра
0
1
2
3
0
1
2
3
0
1
2
3
11

12.

Правило произведения:
• Если элемент А можно выбрать из
множества элементов п способами и для
каждого такого выбора элемент В можно
выбрать т способами, то два элемента
(пару) А и В можно выбрать п·т
способами.
@ Gryznova A.K.
12

13.

«Примеры решения комбинаторных задач: перебор вариантов,
правило суммы, правило умножения».
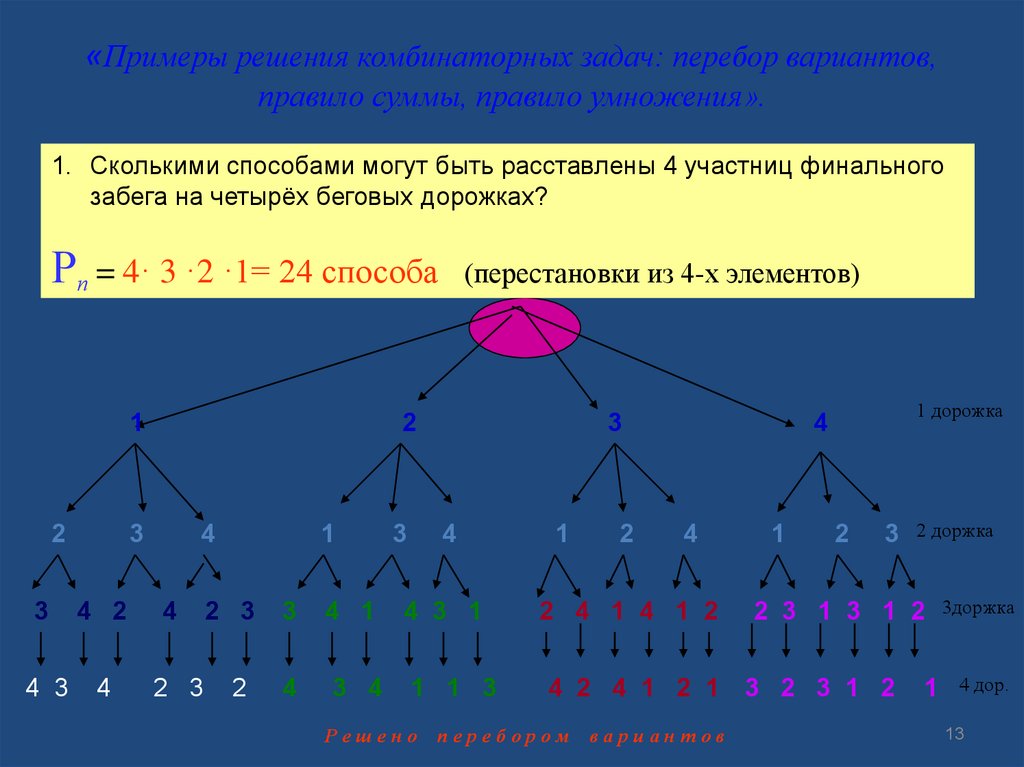
1. Сколькими способами могут быть расставлены 4 участниц финального
забега на четырёх беговых дорожках?
Рп = 4· 3 ·2 ·1= 24 способа (перестановки из 4-х элементов)
1
2
2
3
4
1
3
3
4
1
2
1 дорожка
4
4
1
2
3 2 доржка
3
4 2
4
2 3
3
4 1
4 3 1
2 4 1 4 1 2
2 3 1 3 1 2 3доржка
4 3
4
2 3
2
4
3 4
1 1 3
4 2 4 1 2 1
3 2 3 1 2
Решено перебором вариантов
1
4 дор.
13

14.

II. Перестановки
(1)
К в а рт ет
Проказница Мартышка,
Осёл,
Козёл
Да косолапый Мишка
Затеяли сыграть Квартет.
…………………………………………………….
Ударили в смычки, дерут, а толку нет.
«Стой, братцы, стой! - кричит Мартышка. –
Погодите!
Как музыке идти? Ведь вы не так сидите»
4·3·2·1 = 4! способов
14

15.

II. Перестановки
(2)
• Перестановкой из п - элементов называется
комбинации, отличающиеся друг от друга лишь
порядком следования элементов
• Рп- число перестановок (Р первая буква французского слова
permutation- перестановка)
Рп= n·(n-1)·(n-2)·(n-3)·(n-4)·. . .·3 ·2 ·1= n!
Рп = n!
В математике принято считать 0! =1 и 1! = 1
15

16.

Размещения (1)
• Четыре попутчик решили обменяться визитными карточками.
Сколько всего карточек при этом было использовано?
получилось 12 карточек. Каждый из четырёх
2
3
попутчиков вручил визитку каждому из
трёх попутчиков
4 · 3 = 12
1
4
Комбинации, составленные из k элементов, взятых из n элементов, и
отличающиеся друг от друга либо составом, либо порядком
расположения элементов, называются размещениями из n
элементов по k (0< k ≤n ).
k - размещение из n элементов по k элементов. А первая буква
n французского слова arrangement : «размещение»,
A
«приведение в порядок»
16

17.

Размещения (2)
• Пуст имеется 4 шара и 3 пустых ячейки. Обозначим шары
буквами a, b, c, d. В пустые ячейки можно по разному
разместить три шара из этого набора.
• Выбирая по-разному первый, второй и третий шары, будем
получать различные упорядоченные тройки шаров
a b c
d b c
a c b
b a c
• Каждая упорядоченная тройка, которую можно составить
из четырёх элементов называется размещением из
четырёх элементов по три
k
n n 1 n 2 n 2 ... n k 1 .
n
A
17

18.

Размещения (3)
• Сколько же размещений можно составить
из 4-х элементов (abcd) по три?
• abc
abd
acb
acd
adb
adc
• bac bad
bca
bcd bda bdc
• cab cad
cba
cbd
cda
cdb
• dab dac dba
dbc
dca
dcb
A 4 3 2
3
4
Решено
перебором
вариантов
n
An P n n !
18

19.

Размещения (4)
• Можно решить и не выписывая самих размещений:
• первый элемент можно выбрать четырьмя способами, так
им может быть любой элемент из четырёх;
• для каждого первого второй можно выбрать тремя
способами;
• для каждых первых двух можно двумя способами выбрать
третий элемент из двух оставшихся.
Получаем
3
4
A = 4·3·2 = 24
Решено с использованием
правила
у м н о ж е ни я
19

20.

Сочетания
• Сочетанием из п элементов по k называют
любое множество, составленное из k
элементов, выбранных из п элементов
п!
n n 1 n 2 ... n k 1
k
Cn
C
k ! n k !
1 2 3 ... k
k
n
В отличии от размещений в сочетаниях не имеет
значение порядок элементов. Два сочетания
отличаются друг от друга хотя бы одним
элементом
20

21.

Р е ш и з а д а ч и:
1.
На плоскости отмечено 5 точек.
Сколько получится отрезков, если соединить
точки попарно?
C 52
5!
1 2 3 4 5 3 4 5 2 5 10
2 ! 5 2 ! 1 2 (3!) 1 2 3
2. На окружности отмечено
п точек. Сколько
существует треугольников с вершинами в этих
точках?
C 3п
п 1) п ( п 2 ) ( п 1) п
3!(пп-! 3) ! 1 2 31 ...2 (3п (1 3 2) (3п ...( 2п) (3))
1 2 3
21

22.

Факториал
1! 1,
2!
3!
4!
n!
1,
n!
n (n 1)!,
если
если
n 1,
n 1.
22

23.

Факториал
1! 1,
2! 2 1,
3! 3 2 1
4! 4 3 2 1
n! n (n 1) 2 1
23

24.

Мартышка –
Мишка –
Козёл –
Осёл –
24

25.

25

26.

Домашнее задание.
• 1. В зоопарке 5 львов надо распределить по одному
по пяти клеткам, четырех тигров – по четырем
другим клеткам и трех слонов – по трем вольерам.
• а) Найдите число всех возможных распределений
львов, тигров и слонов в зоопарке.
б) То же, но если есть четыре льва и львица и
одного льва (известно какого именно) вместе с
львицей надо посадить в одну клетку.
в) То же, что и в пункте а), но если у львов есть две
семейные пары.
г) то же, что и в пункте а), но если между клетками
для тигров и клетками для львов нет разницы.
@ Gryznova A.K.
26

27.

Домашнее задание
• Задача № 2. Девятиклассники Женя,
Сережа, Коля, Наташа и Оля побежали на
перемене к теннисному столу,
за которым уже шла игра. Сколькими
способами подбежавшие к
столу пятеро девятиклассников могут
занять
очередь для игры в
настольный теннис?
@ Gryznova A.K.
27

28.

Домашнее задание
• 3. В 9 классе учатся 7 учащихся, в 10 - 9
учащихся, а в 11 - 8 учащихся. Для
работы на пришкольном
участке надо выделить двух учащихся из 9
класса,
трех – из 10, и одного – из 11 .
Сколько существует способов выбора
учащихся для работы на
пришкольном участке?
@ Gryznova A.K.
28

29.

Домашнее задание
• 4.Сколькими способами можно выложить в
ряд красный, черный, синий и
зеленый шарики?
• 5.Сколько различных трехзначных чисел
можно составить из цифр 1, 2, 3, 4, 5,
6, 7, 8, 9 при условии, что в
записи числа каждая цифра используется
только
один раз?
@ Gryznova A.K.
29