Элементы комбинаторики

1.

Элементы
комбинаторики
1

2.

Основные вопросы:
I. Что такое комбинаторика?
Какие задачи считают комбинаторными?
II. Перестановки
III.Размещения
IV.Сочетания
2

3.

Комбинаторика – раздел математики, в
котором рассматриваются задачи о
подсчёте числа комбинаций
составленных по определённым
правилам.
3

4.

II. Какие задачи считают комбинаторными?
Комбинаторные задачи
Задачи подсчёта числа комбинаций из конечного
числа элементов
Комбинаторика – от латинского слова combinare,
что означает «соединять, сочетать».
Методы комбинаторики находят широкое
применение в физике, химии, биологии, экономики
и др. областях знания.
Комбинаторику можно рассматривать как
часть теории множеств – любую комбинаторную
задачу можно свести к задаче о конечных
множествах и их отображениях.
4

5.

I. Уровни решения комбинаторных задач
1. Начальный уровень.
Задачи поиска хотя бы одного решения, хотя бы одного
расположения объектов, обладающих заданным свойствами
- отыскание такого расположения десяти точек на пяти
отрезках, при
котором на каждом отрезке лежит по четыре
точки;
- такого расположения восьми ферзей на шахматной доске,
при котором они не бьют друг друга.
Иногда удаётся доказать, что данная задача не имеет решения
(например, нельзя расположить 10 шаров в 9 урнах так, что
бы в каждой урне было не более одного шара – хотя бы в
одной урне окажется не менее двух шаров).
5

6.

2. Второй уровень.
Если комбинаторная задача имеет несколько решений, то
возникает вопрос о подсчете числа таких решений, описании
всех решений данной задачи.
3. Третий уровень.
Решения данной комбинаторной задачи отличаются друг от
друга некоторыми параметрами. В этом случае возникает
вопрос отыскания оптимального варианта решения такой
задачи.
Например:
Путешественник хочет выехать из города А, посетить
города В, С, и D. После чего вернуться в город А.
6

7.

На рис. изображена схема путей, связывающих эти города.
Различные варианты путешествий отличаются друг от
друга порядком посещения городов В, С, и .D. Существует
шесть вариантов путешествия. В таблице указаны
варианты и длин каждого пути:
Путь
Длина пути
Путь
Длина пути
ABCDA
1555
ACDBA
1300
ABDCA
1300
ADBCA
1450
ACBDA
1450
ADCBA
1550
@ GRYZNOVA A.K.
7

8.

Правила суммы и произведения
1. Сколько различных коктейлей можно составить из четырёх
напитков, смешивая их в равных количествах по два?
AB, AC, AD, BC, BD, CD – всего 6 коктейлей
А
В
D
С
2. Сколько различных двузначных чисел можно составить из цифр
0, 1, 2, 3 ?
Первой цифрой двузначного числа может одна из цифр 1, 2, 3 (цифра 0 не
может быть первой). Если первая цифра выбрана, то вторая может быть любая из
цифр 0, 1, 2, 3. Т.к. каждой выбранной первой соответствует четыре способа
выбора второй, то всего имеется
4 + 4 + 4 = 4·3 = 12
различных двузначных чисел.
8

9.

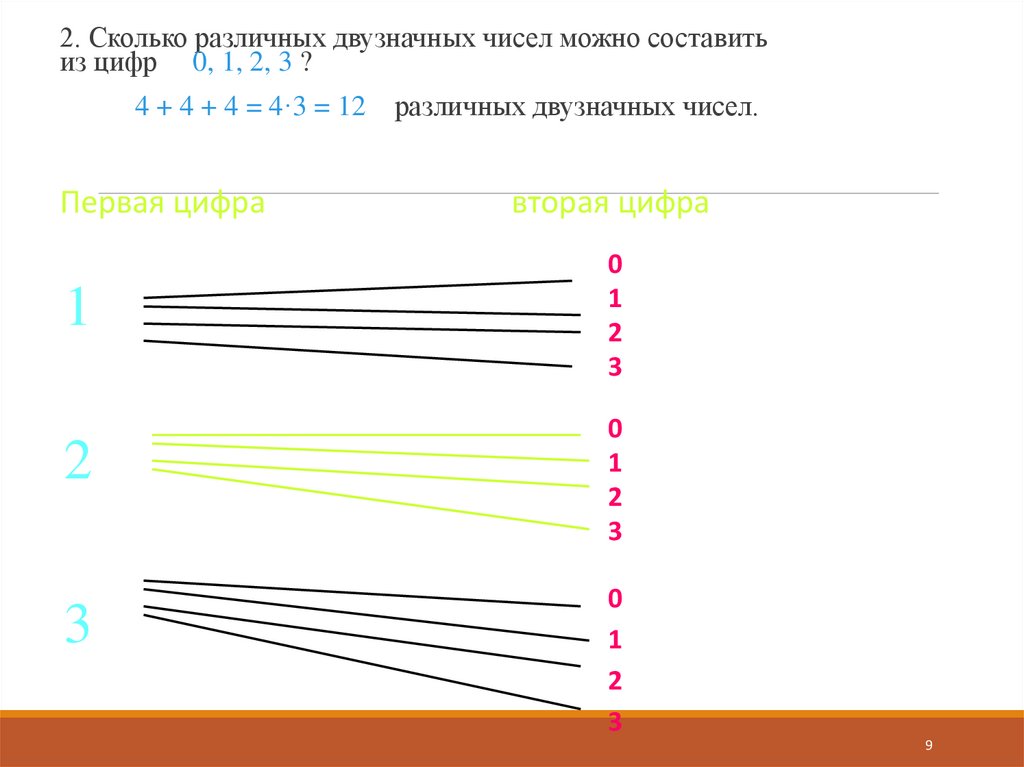
2. Сколько различных двузначных чисел можно составить
из цифр 0, 1, 2, 3 ?
4 + 4 + 4 = 4·3 = 12
Первая цифра
1
2
3
различных двузначных чисел.
вторая цифра
0
1
2
3
0
1
2
3
0
1
2
3
9

10.

Правило произведения:
Если элемент А можно выбрать из
множества элементов п способами и для
каждого такого выбора элемент В
можно выбрать т способами, то два
элемента (пару) А и В можно выбрать
п·т способами.
@ GRYZNOVA A.K.
10

11.

«Примеры решения комбинаторных задач: перебор вариантов,
правило суммы, правило умножения».
1. Сколькими способами могут быть расставлены 4 участниц финального забега
на четырёх беговых дорожках?
Рп = 4· 3 ·2 ·1= 24 способа (перестановки из 4-х элементов)
1
2
3
2
4
1
3
1 дорожка
4
2 доржка
3
4
1
2
4
1
2
3 1
2 4 1 4
1 2
2 3
1 3
1 1 3
4 2 4 1
2 1
3 2 3 1 2 1
3 4 2
4 2 3
3 4 1 4
4 3 4
2 3 2
4
3 4
Решено перебором вариантов
3
1 2 3доржка
4 дор.
11

12.

I Перестановки
Перестановкой из п - элементов называется
комбинации, отличающиеся друг от друга лишь
порядком следования элементов
Рп- число перестановок (Р первая буква французского слова permutationперестановка)
Рп= n·(n-1)·(n-2)·(n-3)·(n-4)·. . .·3 ·2 ·1= n!
Рп = n!
В математике принято считать 0! =1 и 1! = 1
12

13.

Размещения
Четыре попутчик решили обменяться визитными карточками. Сколько
всего карточек при этом было использовано?
получилось 12 карточек. Каждый из четырёх
2
3
попутчиков вручил визитку каждому из
трёх попутчиков
1
4
4 · 3 = 12
Комбинации, составленные из k элементов, взятых из n элементов, и
отличающиеся друг от друга либо составом, либо порядком
расположения элементов, называются размещениями из n
элементов по k (0< k ≤n ).
- размещение из n элементов по k элементов. А первая буква
k
французского слова arrangement : «размещение»,
n
«приведение в порядок»
A
13

14.

Размещения
Пуст имеется 4 шара и 3 пустых ячейки. Обозначим шары буквами a, b, c,
d. В пустые ячейки можно по разному разместить три шара из этого
набора.
Выбирая по-разному первый, второй и третий шары, будем получать
различные упорядоченные тройки шаров
a b c
d b c
a c b
b a c
Каждая упорядоченная тройка, которую можно составить из
четырёх элементов называется размещением из четырёх элементов
по три
k
n n 1 n 2 n 2 ... n k 1 .
n
A
14

15.

Размещения
Сколько же размещений можно составить из 4х элементов (abcd) по три?
abc
abd
acb
acd
adb
adc
bac
bad
bca
bcd
bda
bdc
cab
cad
cba
cbd
cda
cdb
dab
dac
dba
dbc
dca
dcb
A 4 3 2
3
4
Решено перебором вариантов
n
An P n n !
15

16.

Размещения
Можно решить и не выписывая самих размещений:
первый элемент можно выбрать четырьмя способами, так им
может быть любой элемент из четырёх;
для каждого первого второй можно выбрать тремя
способами;
для каждых первых двух можно двумя способами выбрать
третий элемент из двух оставшихся.
Получаем
3
4
A = 4·3·2 = 24
Решено с использованием
правила
у м н о ж е ни я
16

17.

Сочетания
Сочетанием из п элементов по k называют
любое множество, составленное из k элементов,
выбранных из п элементов
п!
n n 1 n 2 ... n k 1
k
Cn
C
k ! n k !
1 2 3 ... k
k
n
В отличии от размещений в сочетаниях не имеет
значение порядок элементов. Два сочетания
отличаются друг от друга хотя бы одним
элементом
17

18.

Р е ш и з а д а ч и:
1.
На плоскости отмечено 5 точек.
Сколько получится отрезков, если соединить
точки попарно?
C 52
5!
1 2 3 4 5 3 4 5 2 5 10
2 ! 5 2 ! 1 2 (3!) 1 2 3
2. На окружности отмечено
п точек. Сколько
существует треугольников с вершинами в этих
точках?
C 3п
п 1) п ( п 2 ) ( п 1) п
3!(пп-! 3) ! 1 2 31 ...2 (3п (1 3 2) (3п ...( 2п) (3))
1 2 3
18