Подсчет вариантов с помощью графов

1.

ГБОУ СОШ № 411 «Гармония» Петродворцового района Санкт-Петербурга
Алгебра
7 класс
Тема урока:
Подсчет вариантов с помощью графов
Учитель: Кащеева Наталья Ивановна
2021

2.

Граф
Граф – это геометрическая фигура,
состоящая из точек и соединяющих их отрезков.
Точки называются вершинами графа, а соединяющие линии – рёбрами.

3.

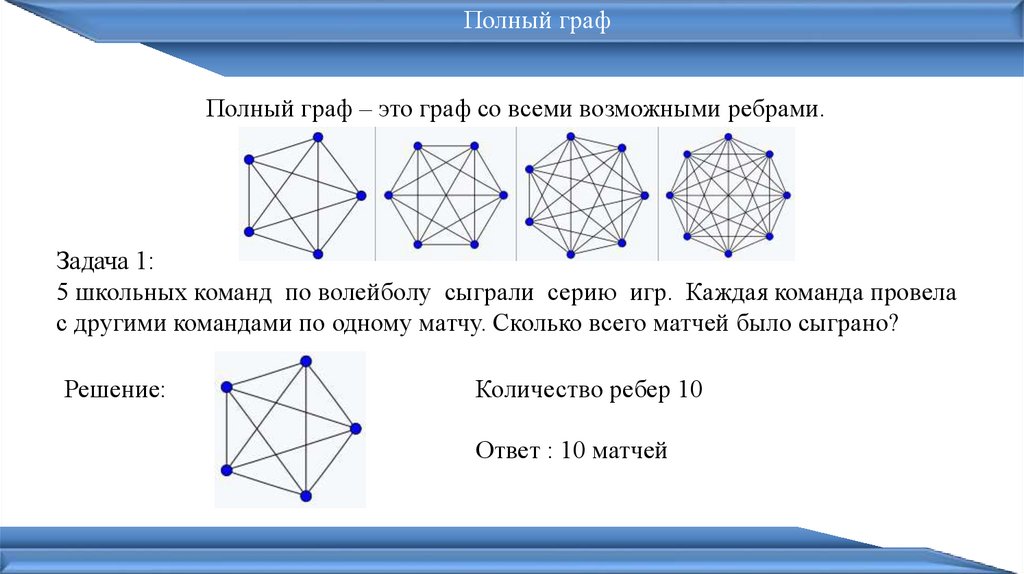
Полный граф
Полный граф – это граф со всеми возможными ребрами.
Задача 1:
5 школьных команд по волейболу сыграли серию игр. Каждая команда провела
с другими командами по одному матчу. Сколько всего матчей было сыграно?
Решение:
Количество ребер 10
Ответ : 10 матчей

4.

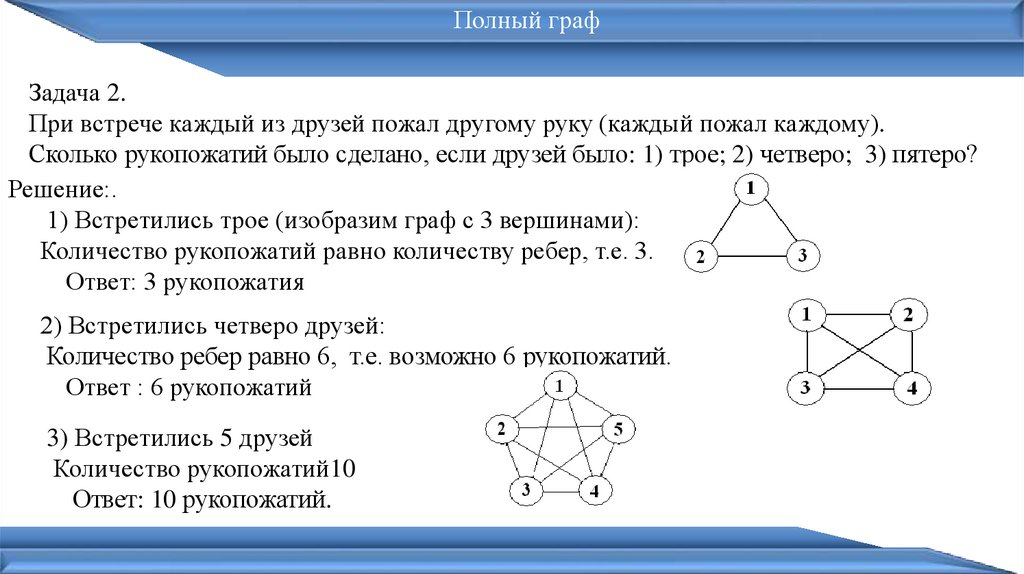
Полный граф
Задача 2.
При встрече каждый из друзей пожал другому руку (каждый пожал каждому).
Сколько рукопожатий было сделано, если друзей было: 1) трое; 2) четверо; 3) пятеро?
Решение:.
1) Встретились трое (изобразим граф с 3 вершинами):
Количество рукопожатий равно количеству ребер, т.е. 3.
Ответ: 3 рукопожатия
2) Встретились четверо друзей:
Количество ребер равно 6, т.е. возможно 6 рукопожатий.
Ответ : 6 рукопожатий
3) Встретились 5 друзей
Количество рукопожатий10
Ответ: 10 рукопожатий.

5.

Полный граф
Задача 3
Сколько ребер имеет полный граф (каждая вершина соединена с каждой),
если количество его вершин n, где 1) n=12, 2) n= 37, 3) n=m?
Решение:
1)
=66.
2)
3)
=1176.

6.

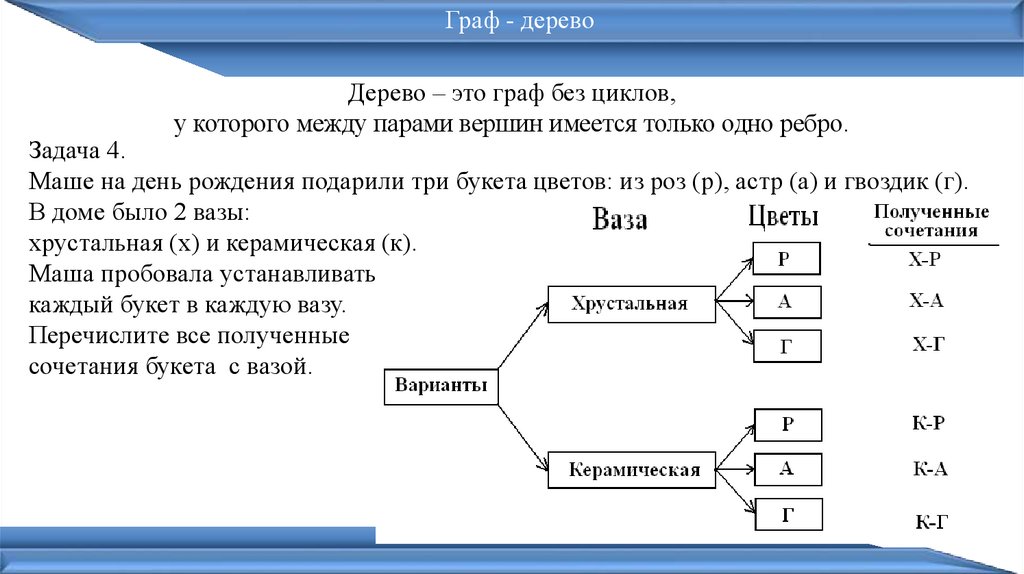
Граф - дерево
Дерево – это граф без циклов,
у которого между парами вершин имеется только одно ребро.
Задача 4.
Маше на день рождения подарили три букета цветов: из роз (р), астр (а) и гвоздик (г).
В доме было 2 вазы:
хрустальная (х) и керамическая (к).
Маша пробовала устанавливать
каждый букет в каждую вазу.
Перечислите все полученные
сочетания букета с вазой.

7.

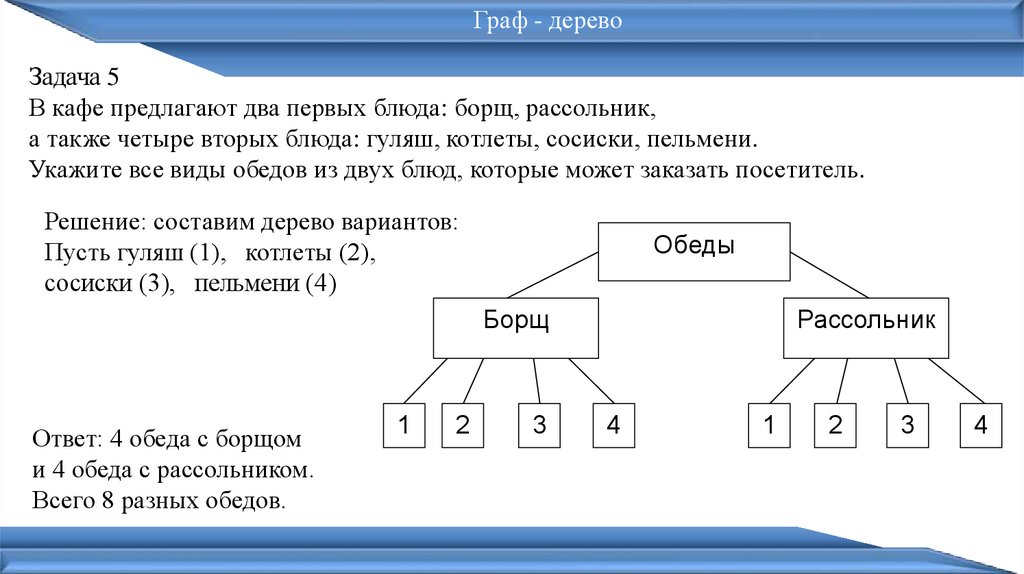
Граф - дерево
Задача 5
В кафе предлагают два первых блюда: борщ, рассольник,
а также четыре вторых блюда: гуляш, котлеты, сосиски, пельмени.
Укажите все виды обедов из двух блюд, которые может заказать посетитель.
Решение: составим дерево вариантов:
Пусть гуляш (1), котлеты (2),
сосиски (3), пельмени (4)
Обеды
Борщ
Ответ: 4 обеда с борщом
и 4 обеда с рассольником.
Всего 8 разных обедов.
1
2
3
Рассольник
4
1
2
3
4

8.

Граф - дерево
Задача 6
Сколько различных трехзначных чисел можно записать с помощью цифр 5, 6, 7
при условии, что цифры могут повторяться?
варианты
5
6
5
5
7
6
Ответ : 27
5
7
5
7
6
7
6
5
6
5
5
7
7
6
5
5
7
6
5
7
6
6
7
7
6
7
6
5
7
6
5
7
6

9.

Перестановки
Задача 7
Антон, Борис, Виктор и Даниил купили 4 билета в театр на 1, 2, 3 и 4 места десятого ряда.
Сколько существует различных способов, которыми мальчики могут занять эти места?
Решение:
Согласно правилу произведения число таких способов 4·3·2·1=24
Ответ: 24
Число всевозможных перестановок из четырех элементов Р4 = 4·3·2·1.
В комбинаторике число всевозможных перестановок из n элементов обозначают
Рn. =1·2·3·4·…·(n-1)·n= n!
Произведение первых n натуральных чисел обозначают n!
0!=1 и 1!=1.

10.

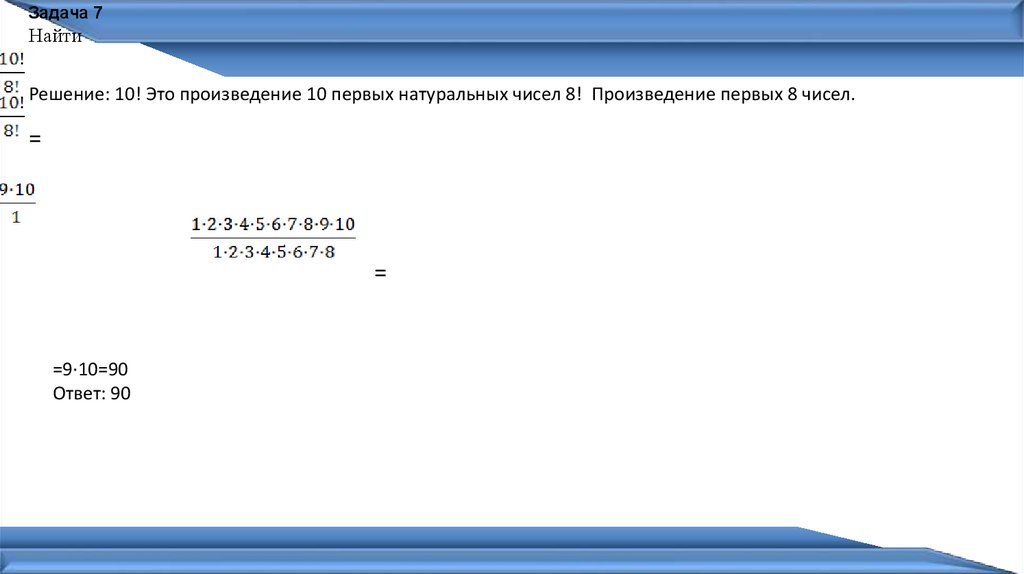
Задача 7
Найти
Решение: 10! Это произведение 10 первых натуральных чисел 8! Произведение первых 8 чисел.
=
=
=9·10=90
Ответ: 90