Атомная физика. Атом Бора. Квантовая теория атома (лекция 6)

1.

Физика. 2 курс. 4 семестр
Специалитет
Лекция 6. Атомная физика
- Атом Бора
- Квантовая теория атома
В.И. Читайкин
кандидат физико-математических наук
доцент

2.

План лекции
Наименование раздела, параграфа
Номер
слайда
Наименование раздела, параграфа
Номер
слайда
Введение
3
Раздел 2. Квантовая теория атома
20
Предисловие. Прошлые идеи, не канувшие в Лету.
4
2.1. Основные положения
21
1. Модель атома Томсона – «пудинг»
5
2.2. Уравнение Шредингера для водородоподобного атома
22
2. Планетарная модель атома Резерфорда
7
2.2.1. Потенциальная энергия (потенциал)
22
3. Противоречия в модели атома Резерфорда
8
2.2.2. Стационарное уравнение Шредингера: общий вид
23
Раздел 1. Модель атома Бора
9
24
1.1. Постулаты Бора
10
2.2.3. Стационарное уравнение Шредингера: в
сферических координатах
1.2. Расчёты параметров атома водорода
12
2.3. Разделение переменных в уравнении Шредингера
26
1.2.1. Расчёт радиуса атома водорода
12
1.2.2. Расчёт энергетических уровней атома водорода
13
1.2.3. Расчёт энергии переходов между уровнями атома
водорода
14
1.2.4. Сериальная формула для атома водорода
16
1.3. Водородоподобные атомы (ионы)
17
1.4. Недостатки модели атома Бора
18
Иллюстрация
19
2

3.

Введение
Этой лекцией мы начинаем курс «Атомная физика». В течение шести лекций, с 6-ой по 11-ую,
будут последовательно рассмотрены физические эффекты атома и, в последней лекции, атомного
ядра. Рассмотрение основано на квантово-физическом подходе, его основных понятиях и
закономерностях, которые были представлены в первых пяти лекциях семестра.
Первая лекция курса «Атомная физика», она же 6-ая лекция в семестре, начинается с небольшого
исторического предисловия, которое позволяет увидеть «тяжёлую поступь» развития научной теории.
Раздел 1-ый лекции – это модель атома Бора, которая также «ушла в прошлое». Но её основные
идеи оказались полезными в дальнейшем, а понятия (определения, названия) сохранились до сих пор
и активно используются. Не вполне официально, теория Бора носит название «полуклассической».
Раздел 2-ой лекции – это начало рассмотрения квантовой теории атома. Как и полагается в любой
задаче квантовой физики, сначала формулируется уравнение Шредингера и определяется вид
потенциальной энергии. Далее, уравнение Шредингера переписывается в сферических координатах
как наиболее подходящих для атома – ведь атом очень похож на шарик…
Традиционно, рассматривается стационарный случай уравнения Шредингера.
3

4.

Предисловие. Прошлые идеи, не канувшие в Лету.
4

5.

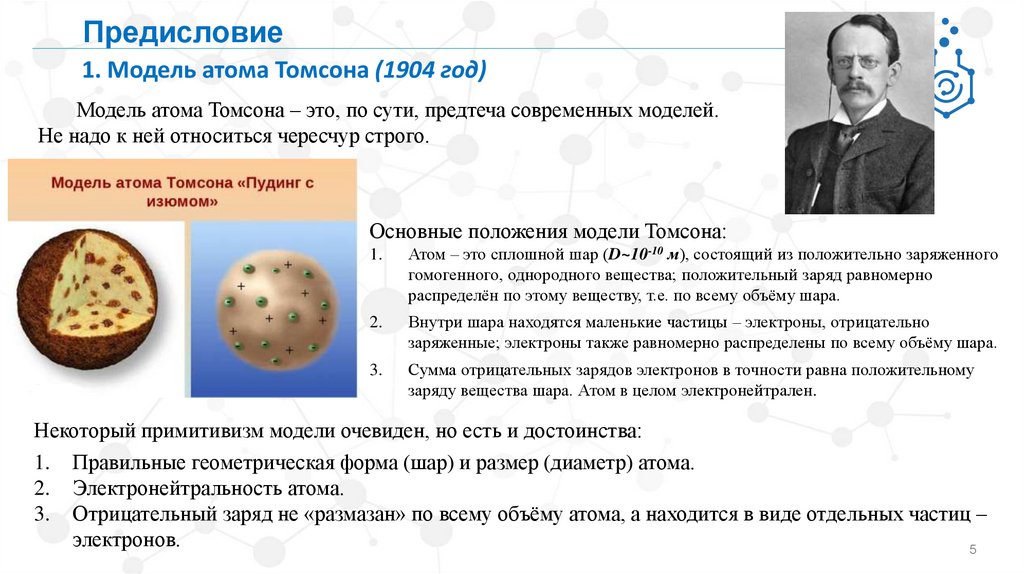
Предисловие
1. Модель атома Томсона (1904 год)
Модель атома Томсона – это, по сути, предтеча современных моделей.
Не надо к ней относиться чересчур строго.
Основные положения модели Томсона:
1.
Атом – это сплошной шар (D~10-10 м), состоящий из положительно заряженного
гомогенного, однородного вещества; положительный заряд равномерно
распределён по этому веществу, т.е. по всему объёму шара.
2.
Внутри шара находятся маленькие частицы – электроны, отрицательно
заряженные; электроны также равномерно распределены по всему объёму шара.
3.
Сумма отрицательных зарядов электронов в точности равна положительному
заряду вещества шара. Атом в целом электронейтрален.
Некоторый примитивизм модели очевиден, но есть и достоинства:
1. Правильные геометрическая форма (шар) и размер (диаметр) атома.
2. Электронейтральность атома.
3. Отрицательный заряд не «размазан» по всему объёму атома, а находится в виде отдельных частиц –
электронов.
5

6.

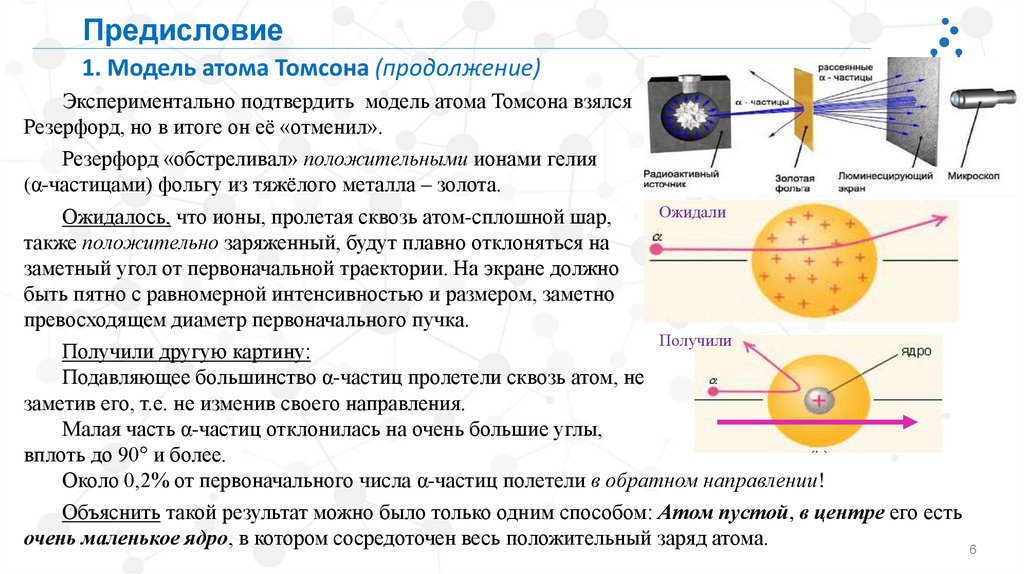
Предисловие
1. Модель атома Томсона (продолжение)
Экспериментально подтвердить модель атома Томсона взялся
Резерфорд, но в итоге он её «отменил».
Резерфорд «обстреливал» положительными ионами гелия
(α-частицами) фольгу из тяжёлого металла – золота.
Ожидали
Ожидалось, что ионы, пролетая сквозь атом-сплошной шар,
также положительно заряженный, будут плавно отклоняться на
заметный угол от первоначальной траектории. На экране должно
быть пятно с равномерной интенсивностью и размером, заметно
превосходящем диаметр первоначального пучка.
Получили
Получили другую картину:
Подавляющее большинство α-частиц пролетели сквозь атом, не
заметив его, т.е. не изменив своего направления.
Малая часть α-частиц отклонилась на очень большие углы,
вплоть до 90° и более.
Около 0,2% от первоначального числа α-частиц полетели в обратном направлении!
Объяснить такой результат можно было только одним способом: Атом пустой, в центре его есть
очень маленькое ядро, в котором сосредоточен весь положительный заряд атома.
6

7.

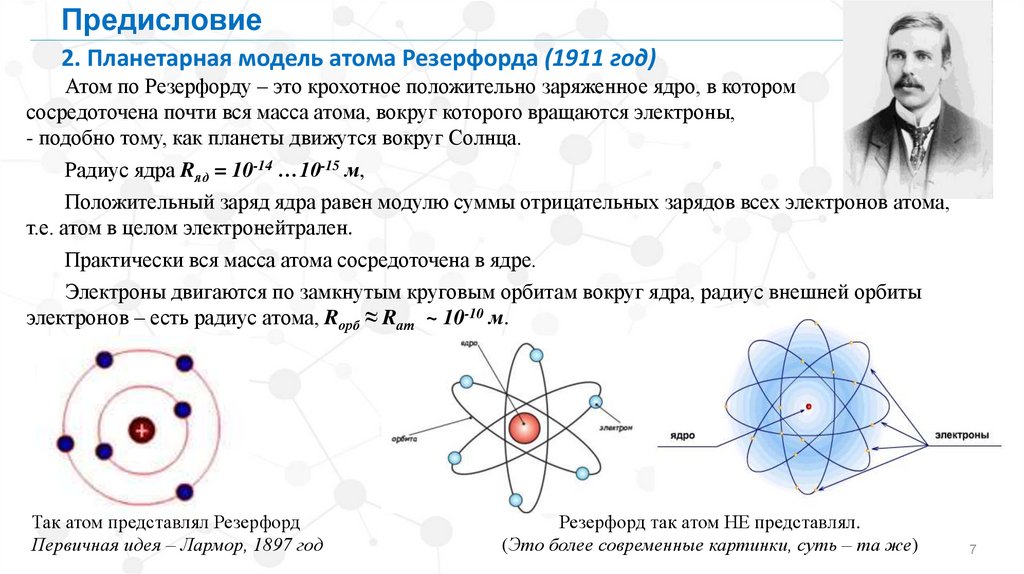
Предисловие
2. Планетарная модель атома Резерфорда (1911 год)
Атом по Резерфорду – это крохотное положительно заряженное ядро, в котором
сосредоточена почти вся масса атома, вокруг которого вращаются электроны,
- подобно тому, как планеты движутся вокруг Солнца.
Радиус ядра Rяд = 10-14 …10-15 м,
Положительный заряд ядра равен модулю суммы отрицательных зарядов всех электронов атома,
т.е. атом в целом электронейтрален.
Практически вся масса атома сосредоточена в ядре.
Электроны двигаются по замкнутым круговым орбитам вокруг ядра, радиус внешней орбиты
электронов – есть радиус атома, Rорб ≈ Rат ~ 10-10 м.
Так атом представлял Резерфорд
Первичная идея – Лармор, 1897 год
Резерфорд так атом НЕ представлял.
(Это более современные картинки, суть – та же)
7

8.

Предисловие
4. Противоречия в планетарной модели атома Резерфорда
Как только Резерфорд сформулировал свои представления по планетарной модели атома, так тут
же ему было указано, что такая модель невозможна.
Действительно, электрон, вращаясь по круговой орбите, движется с ускорением.
Величина ускорения огромна ае ~ 1022 м/с2. Линейная скорость движения электрона ve ~ 106 м/с. (Получите эти значения
самостоятельно, приравняв центробежную силу и силу Кулона.)
Ускоренно движущееся заряженное тело (электрон) создаёт вокруг себя электромагнитное поле
(вспомните лекции по теории Максвелла); т.е. электрон должен излучать электромагнитные волны.
Непрерывно излучающий электрон теряет энергию; теряя энергию, вращающийся электрон
переходит на более низкую орбиту, приближаясь к ядру. За время ~10-8 с электрон должен упасть на
ядро, значит, атом должен прекратить существование.
Противоречия в планетарной модели Резерфорда (расхождение с опытными данными):
1. Атом неустойчив. Окружающего мира быть не должно. Но он есть!
2. Спектр излучения атома непрерывен. Но в экспериментах наблюдается ярко выраженный
линейчатый спектр.
Требовалось дальнейшее совершенствование модели атома. И тут пришёл Бор …
8

9.

Раздел 1. Модель атома Бора
9

10.

1. Модель атома Бора
1.1. Постулаты Бора
Бор устранил основное противоречие планетарной модели Резерфорда (а именно:
атомы должны излучать непрерывно и очень быстро прекращать своё существование),
но каким способом! Бор просто-напросто запретил атомам излучать! Это была
гениальная догадка, полностью подтвердившаяся впоследствии.
Постулаты Бора.
1-ый постулат. В атоме существуют стационарные состояния, в которых он (атом) не
излучает энергии. Другими словами, движение электрона по таким круговым стационарным
орбитам не сопровождается излучением.
Такие стационарные орбиты дискретны, т.е. их радиусы не случайны,
а располагаются в строгой последовательности: rn, n = 1, 2, 3 …
Значения rn определяются из условия «квантования» момента импульса
электрона (L), вращающегося на n-ой орбите со скоростью v:
L = me·v·rn = n·h/2π,
n = 1, 2, 3 …
h – постоянная Планка
О
Физсмысл 1-ого постулата: момент импульса пропорционален числу n, поэтому он не может
принимать произвольные значения, только дискретные. Поэтому и радиусы орбит электрона
будут дискретны: rn ~ n.
v
m
r
10

11.

1. Модель атома Бора
1.1. Постулаты Бора (продолжение)
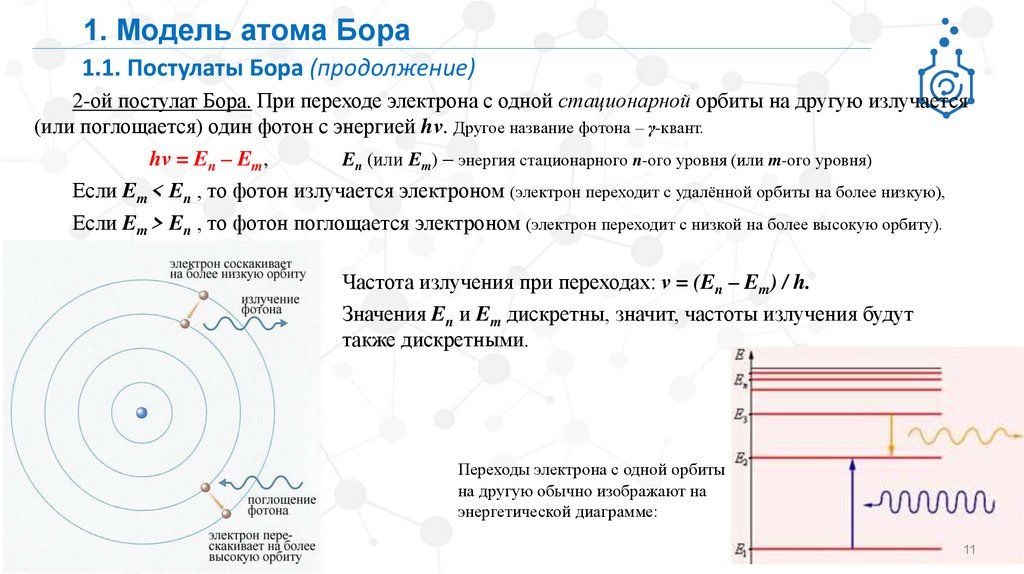
2-ой постулат Бора. При переходе электрона с одной стационарной орбиты на другую излучается
(или поглощается) один фотон с энергией hν. Другое название фотона – γ-квант.
hν = En – Em,
En (или Em) – энергия стационарного n-ого уровня (или m-ого уровня)
Если Em < En , то фотон излучается электроном (электрон переходит с удалённой орбиты на более низкую),
Если Em > En , то фотон поглощается электроном (электрон переходит с низкой на более высокую орбиту).
Частота излучения при переходах: ν = (En – Em) / h.
Значения En и Em дискретны, значит, частоты излучения будут
также дискретными.
Переходы электрона с одной орбиты
на другую обычно изображают на
энергетической диаграмме:
11

12.

1. Модель атома Бора
1.2. Расчёты параметров атома
Наиболее точные расчёты параметров атома можно выполнить по модели Бора для простейшего
атома – атома водорода.
1.2.1. Расчёт радиуса атома водорода
Запишем систему 2-х уравнений:
(1) me·v·rn = n·h/2π – первый постулат Бора;
– уравнение движения электрона по орбите: центростремительная сила равна силе Кулона.
(2)
В системе два уравнения и два неизвестных (скорость v и радиус r), остальное – параметры и
постоянные (Z – число электронов в атоме, или заряд ядра, т.е. порядковый номер в таблице Менделеева).
Решение системы уравнений даёт следующие значения радиусов орбит в атоме Бора:
(3)
ℏ = h/2π
Важно: rn ~ n2
Получите уравнение (3) самостоятельно.
1-ый боровский радиус для водорода (n=1, Z=1): r1 = a ≈ 0,5·10-10 м.
Рассчитанное по модели Бора значение r1 хорошо соответствует более поздним расчётам и опытам.
12

13.

1. Модель атома Бора
1.2.2. Расчёт энергетических уровней атома водорода
Полная энергия электрона в атоме: Е = Екин + Епот = m·v2/2 + (- Fкул ·r).
Используя уравнение (2) и формулу (3) для радиуса (см. предыдущий слайд), получим:
Получите уравнение (4) самостоятельно.
(4)
Важно: Еn ~ 1/n2. Линии сгущаются по мере
роста энергии.
Знак «минус» в формуле (4) означает, что электроны находятся в
связанном состоянии, т.е. располагаются на орбитах внутри атома.
Значение Е = 0 соответствует «границе» атома:
- при Е < 0 электроны связаны, т.е. находятся в атоме;
- при Е > 0 электроны свободны, т.е. находятся за пределами атома.
Формально, значение Е=0 достигается при n=∞.
n – главное квантовое число атома,
n = 1 – основное (нормальное) состояние (основной уровень),
n > 1 – возбуждённое состояние (возбуждённые уровни).
Для водорода: Еmin = En=1 = -13,6 эВ – хорошо совпадает с экспериментом.
Энергетические уровни
атома водорода по Бору
13

14.

1. Модель атома Бора
1.2.3. Расчёт энергии переходов между уровнями атома водорода
В соответствии со 2-ым постулатом Бора, энергия фотона (γ-кванта), излучаемого атомом, есть
разница энергий начального, верхнего уровня (номер n) и конечного, нижнего уровня (номер m):
hν = En – Em ,
m = 1, 2, 3 …
n = m+1, m+2, m+3 …
Используя формулу (4) – см. предыдущий слайд, можно получить частоту излучения ν:
(5)
Параметр R – это универсальная постоянная Ридберга:
m – масса электрона
Замечательно, что частота излучения атома определяется только порядковыми номерами
начального (n) и конечного (m) энергетических уровней в атоме.
14

15.

1. Модель атома Бора
1.2.3. Расчёт энергии переходов между уровнями атома водорода (продолжение)
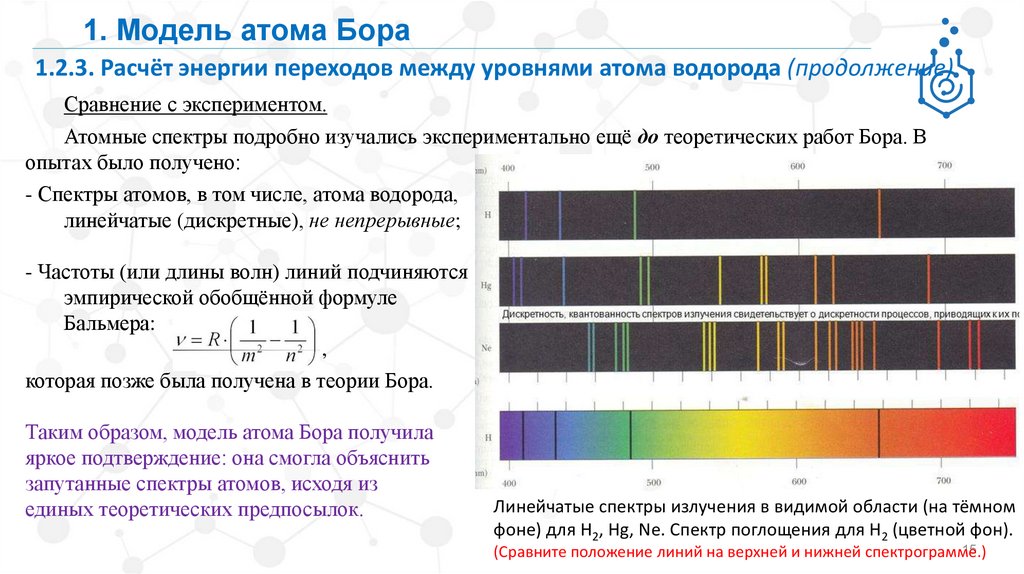
Сравнение с экспериментом.
Атомные спектры подробно изучались экспериментально ещё до теоретических работ Бора. В
опытах было получено:
- Спектры атомов, в том числе, атома водорода,
линейчатые (дискретные), не непрерывные;
- Частоты (или длины волн) линий подчиняются
эмпирической обобщённой формуле
Бальмера:
,
которая позже была получена в теории Бора.
Таким образом, модель атома Бора получила
яркое подтверждение: она смогла объяснить
запутанные спектры атомов, исходя из
единых теоретических предпосылок.
Линейчатые спектры излучения в видимой области (на тёмном
фоне) для H2, Hg, Ne. Спектр поглощения для Н2 (цветной фон).
15
(Сравните положение линий на верхней и нижней спектрограмме.)

16.

1. Модель атома Бора
1.2.4. Сериальная формула для атома водорода
Повторим формулу (5), см. слайд 14:
(5)
Значения n и m – номера начального, верхнего и конечного, нижнего энергетических уровней,
соответственно. Уровни n и m – стационарные уровни атома; значения n и m – это значения главного квантового чосла.
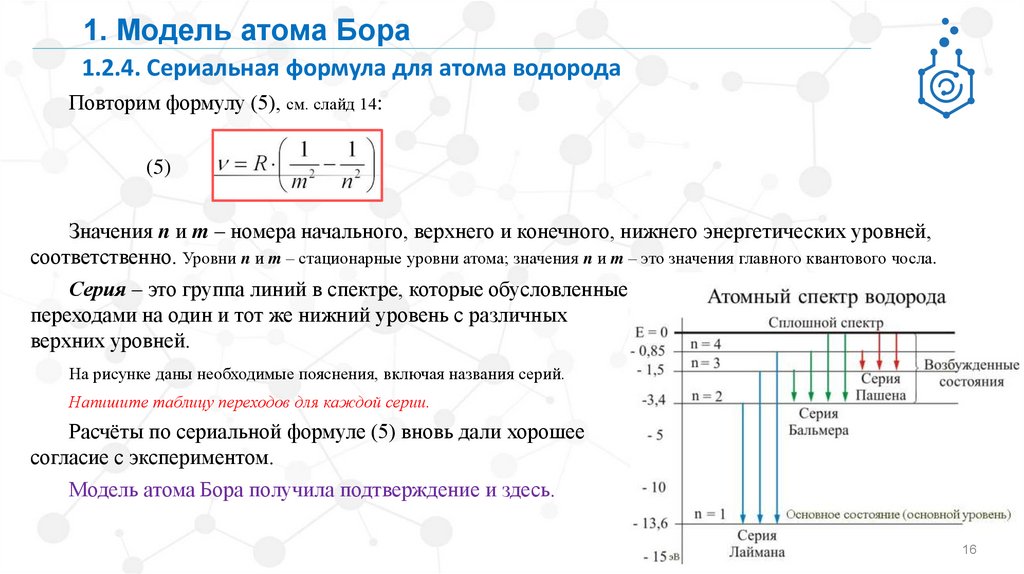
Серия – это группа линий в спектре, которые обусловленные
переходами на один и тот же нижний уровень с различных
верхних уровней.
На рисунке даны необходимые пояснения, включая названия серий.
Напишите таблицу переходов для каждой серии.
Расчёты по сериальной формуле (5) вновь дали хорошее
согласие с экспериментом.
Модель атома Бора получила подтверждение и здесь.
16

17.

1. Модель атома Бора
1.3. Водородоподобные атомы
Определение: водородоподобные атомы – это атомы, состоящие из ядра с положительным
зарядом Z·e и одного электрона с зарядом –е. Водородоподобные атомы – это, фактически, ионы.
Такие водородоподобные атомы (, точнее, ионы) получаются в результате однократной или
многократной ионизации, когда у атома остаётся только один электрон. Например: He+, Li2+ , Be3+ …
Модель атома Бора для водородоподобных атомов, как и для атома водорода, позволяет
рассчитать спектр излучения:
ν = Z2 ·
Эта формула оказалась также вполне рабочей, она давала, в целом, неплохое соответствие с
экспериментальными результатами. Но с ростом Z точность резко падала. Также для атомов с более,
чем двумя электронами, модель атома Бора оказалась неприменимой.
Потребовалась другая модель, точнее, другая физика – квантовая. Это – тема последующих
лекций.
17

18.

1. Модель атома Бора
1.4. Недостатки модели атома Бора
1. Принципиальная неясность основных положений модели атома Бора.
В модели атома Бора электрон, вращающийся вокруг ядра по орбите, не излучает энергии.
Почему? Потому что электрону запретил излучать Нильс Бор!?
Такой ответ, при всём уважении к гениальному человеку, не мог удовлетворить физиков.
2. Ограниченность применения модели атома Бора.
Для атомов с двумя и более электронами, как и для атома с Z > 2, модель атома Бора оказалась
полностью неприменимой.
Даже для атома водорода и водородоподобных атомов модель Бора не позволяла рассчитать
интенсивность спектральных линий, только положение этих линий, т.е. только значения частот
(энергий) межуровневых переходов.
Вывод: теория атома Бора неполна, непоследовательна и, по сути, неверна.
К чести самого Бора, он рассматривал свою модель атома как промежуточный этап и сразу и
безоговорочно поддержал создание и развитие модели атома на основе квантовой физики.
18

19.

1. Модель атома Бора
Иллюстрация: современная «фотография» атома водорода
Синее
кольцо.
Сравните с рисунками на сл. 7. Попробуйте объяснить синее кольцо.
19

20.

Раздел 2. Квантовая теория атома
20

21.

2. Квантовая теория атома
2.1. Основные положения
Суть квантовой теории атома.
Атом – это совокупность электронных «облаков» вокруг ядра атома.
Согласно квантовой теории, понятие «траектория движения электрона вокруг ядра» не
рассматривается, «положение электрона» означает некоторую область пространства, вероятность
нахождения электрона в которой имеет наибольшую величину.
Вероятность нахождения электрона определяется в результате решения соответствующего
уравнения Шредингера, что позволяет в итоге установить «форму» и «плотность» электронных
«облаков».
Теоретико-математические основы квантовой теории атома:
- корпускулярно-волновой дуализм Луи д’Бройля;
- принцип неопределённостей Гейзенберга;
- волновое уравнение Шредингера.
21

22.

2. Квантовая теория атома
2.2. Уравнение Шредингера для водородоподобного атома
Напомню определение водородоподобного атома (см. слайд 17), точнее, одноэлектронного атома:
Водородоподобные атомы – это атомы, состоящие из ядра с зарядом «плюс Z·e» и одного электрона
с зарядом «минус е».
Водородоподобные атомы:
- при Z > 1: это – ионы, полученные из атомов после «обдирания» всех электронов, кроме одного;
- при Z = 1: это – собственно атом водорода.
2.2.1. Потенциальная энергия (потенциал)
Потенциальная энергия кулоновского взаимодействия электрона
с ядром:
где r – расстояние между точечным ядром и точкой,
в которой может быть электрон.
Получите эту формулу самостоятельно, вспомнив
электростатику.
Важно: потенциал в атоме зависит только от расстояния r и не
зависит от других координат (от угловых координат – в полярной
системе). Потенциал U(r) – строго сферически-симметричный!
22

23.

2. Квантовая теория атома
2.2. Уравнение Шредингера для водородоподобного атома (продолжение)
2.2.2. Стационарное уравнение Шредингера: общий вид
Стационарное уравнение Шредингера для произвольного вида потенциальной энергии и
пространства произвольной размерности:
где Δψ – лапласиан: сумма вторых производных по всем координатам
рассматриваемого пространства
Стационарное уравнение Шредингера для водородоподобного атома (потенциал U(r) имеет конкретный
вид – см. предыдущий слайд):
где m – масса электрона, Е – полная энергия.
Замечание: знак лапласиана (Δ) иногда может заменяться на другой (
- «набла 2»); тогда уравнение Шредингера
выглядит так:
. Обе формы уравнения эквивалентны.
Во втором слагаемом в скобках есть ошибка, исправьте её!
23

24.

2. Квантовая теория атома
2.2. Уравнение Шредингера для водородоподобного атома (продолжение)
2.2.3. Стационарное уравнение Шредингера: в сферических координатах
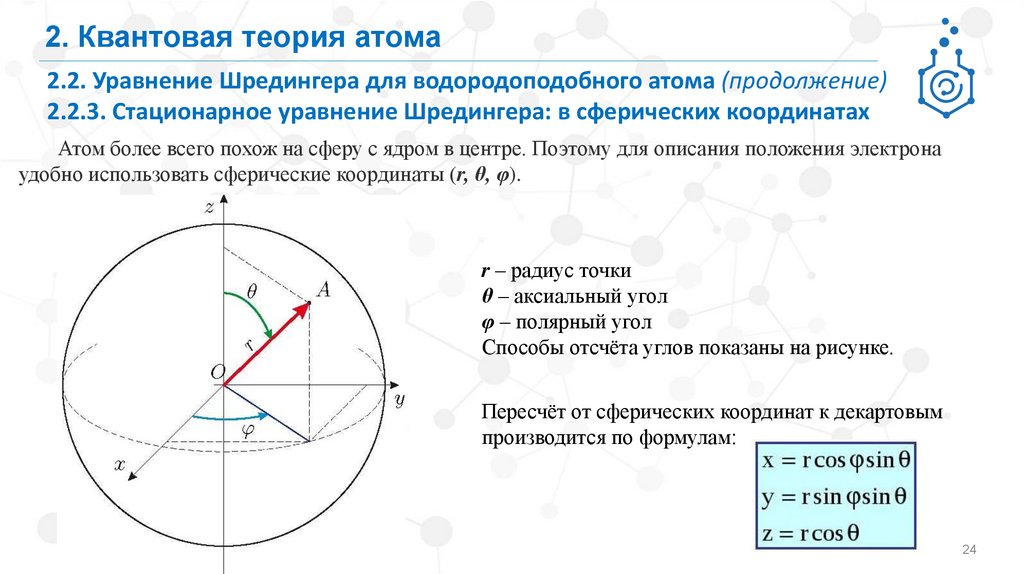
Атом более всего похож на сферу с ядром в центре. Поэтому для описания положения электрона
удобно использовать сферические координаты (r, θ, φ).
r – радиус точки
θ – аксиальный угол
φ – полярный угол
Способы отсчёта углов показаны на рисунке.
Пересчёт от сферических координат к декартовым
производится по формулам:
24

25.

2. Квантовая теория атома
2.2. Уравнение Шредингера для водородоподобного атома (продолжение)
2.2.3. Стационарное уравнение Шредингера: в сферических координатах (продолжение)
Уравнение Шредингера в сферической системе координат для электрона, находящегося в
водородоподобном атоме, имеет вид:
В последнем слагаемом есть
две неточности, исправьте их!
Первые три слагаемые – это лапласиан, записанный в сферических (полярных) координатах (r, θ, φ).
Важно (очень!): несмотря на то, что потенциал в атоме зависит только от одной координаты (r),
уравнение Шредингера явно содержит зависимость от двух других координат: угол θ и угол φ. Значит,
решение уравнения, т.е. волновая функция, также будет в общем случае зависеть от всех трёх координат:
ψ(r, θ, φ).
Решение этого уравнения в общем случае требует больших вычислительных мощностей; для
анализа физических особенностей поведения электрона оно, по сути, малопригодно.
25

26.

2. Квантовая теория атома
2.3. Разделение переменных в уравнении Шредингера
Решение уравнения Шредингера существенно упрощается, если волновую функцию представить в
виде произведения двух функций:
ψ(r, θ, φ) = R(r)·Y(θ, φ),
Использование этого математического приёма (разделение переменных)
оправдано только для основного состояния атома.
где R(r) – радиальная часть волновой функции
Y(θ, φ) – угловая часть волновой функции
Тогда уравнение Шредингера для радиальной части волновой функции в сферических координатах
существенно упрощается:
Здесь ψ = R(r). Зависимость от других, угловых координат
отсутствует.
Е
Уравнение приведено для атома водорода, Z=1.
Напишите уравнение для водородоподобного атома.
Уравнение Шредингера для угловой части волновой функции Y(θ, φ) остаётся угрожающесложным. Впрямую оно пока не будет использоваться, поэтому не приведено.
Попробуйте написать уравнение для Y(θ, φ).
26

27.

Спасибо за внимание