Показательная функция, её свойства и график. Алгебра. 10 класс

1.

Тема урока:
Алгебра 10 класс
Разработал: учитель математики Михеева И.А.

2.

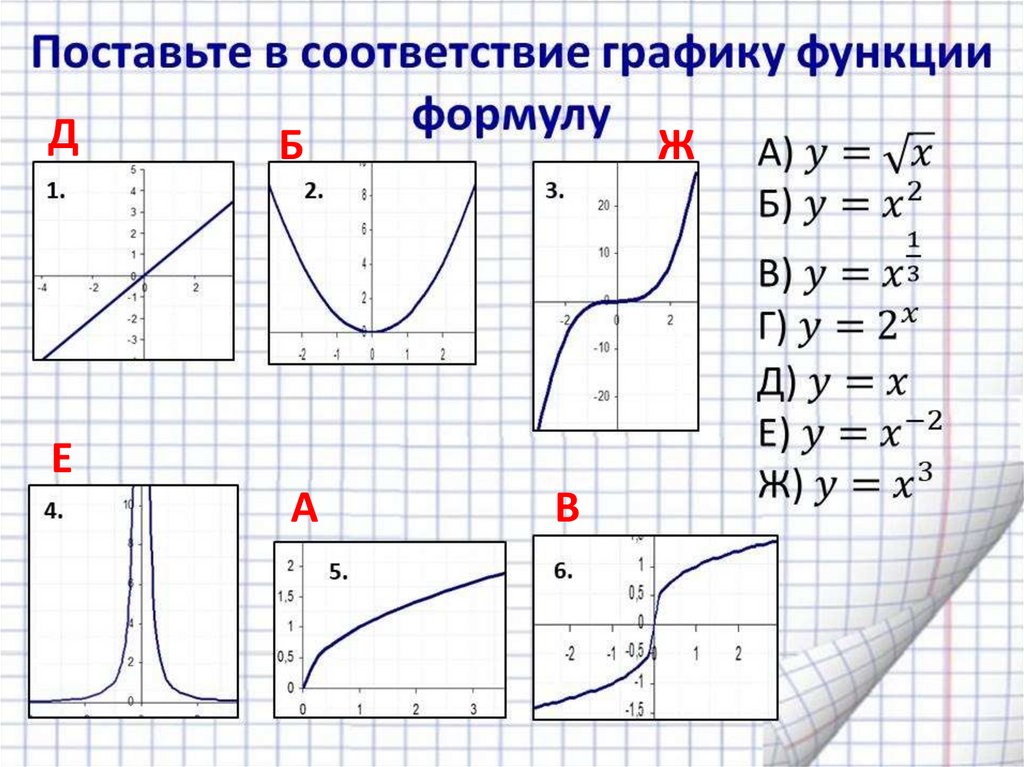
Д
Б
Ж
Е
А
В

3.

4.

5.

6.

Показательная функция
x
y=a
(a>0, a≠1)
y
x
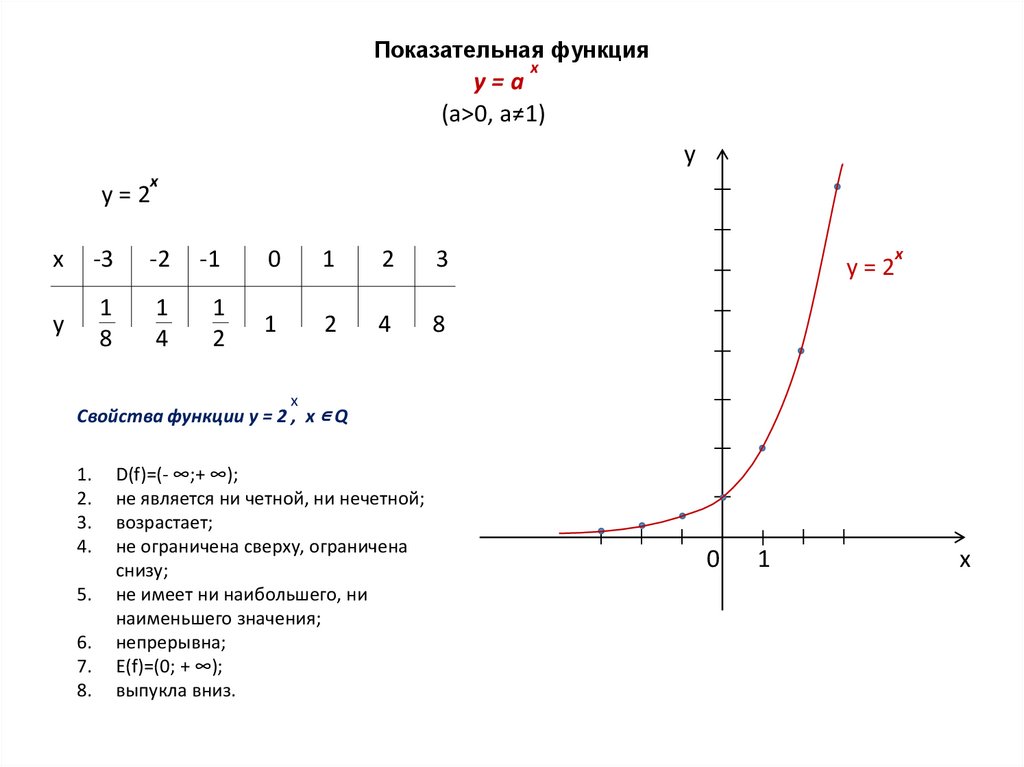
y=2
x
-3
-2
-1
0
1
2
3
y
1
8
1
4
1
2
1
2
4
8
x
y=2
x
Свойства функции y = 2 , x ∊ Q
1.
2.
3.
4.
5.
6.
7.
8.
D(f)=(- ∞;+ ∞);
не является ни четной, ни нечетной;
возрастает;
не ограничена сверху, ограничена
снизу;
не имеет ни наибольшего, ни
наименьшего значения;
непрерывна;
E(f)=(0; + ∞);
выпукла вниз.
0
1
x

7.

Показательная функция
x
y=a
(a>0, a≠1)
y =(
1
2)
y
x
x
-3
-2
-1
0
1
2
3
y
8
4
2
1
1
2
1
4
1
8
1 x
y =( )
2
x
1
Свойства функции y =
, x∊Q
2
()
1.
2.
3.
4.
5.
6.
7.
8.
D(f)=(- ∞;+ ∞);
не является ни четной, ни нечетной;
убывает;
не ограничена сверху, ограничена
снизу;
не имеет ни наибольшего, ни
наименьшего значения;
непрерывна;
E(f)=(0; + ∞);
выпукла вниз.
0
1
x

8.

Показательная функция
x
y=a
(a>0, a≠1)
x
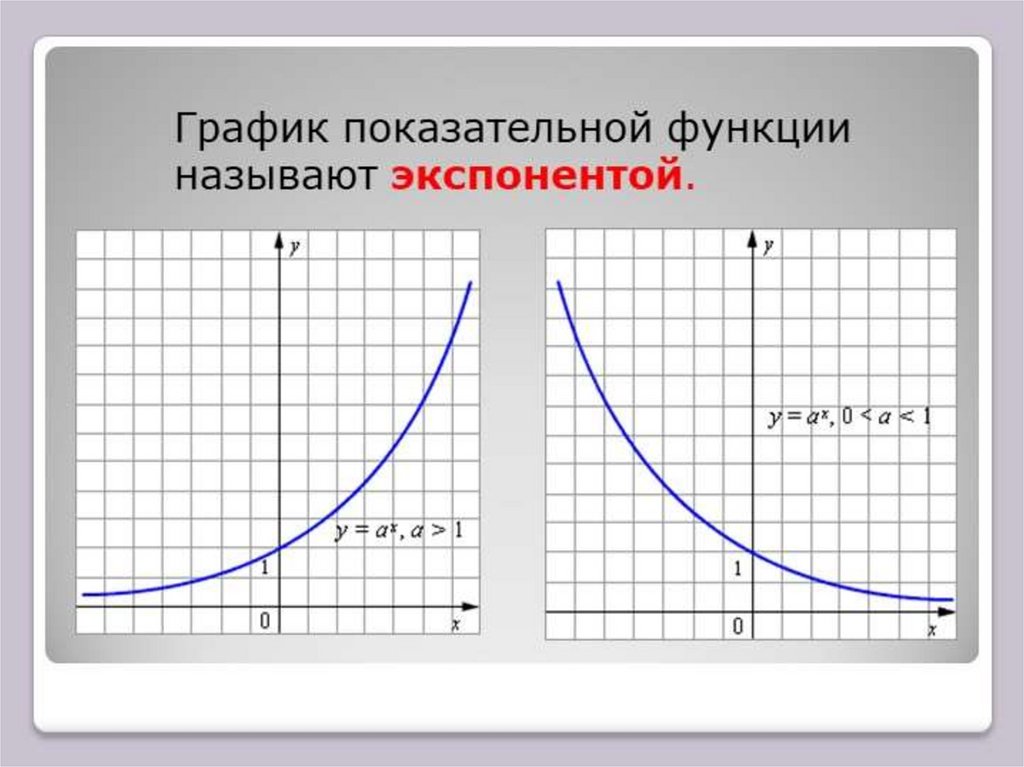
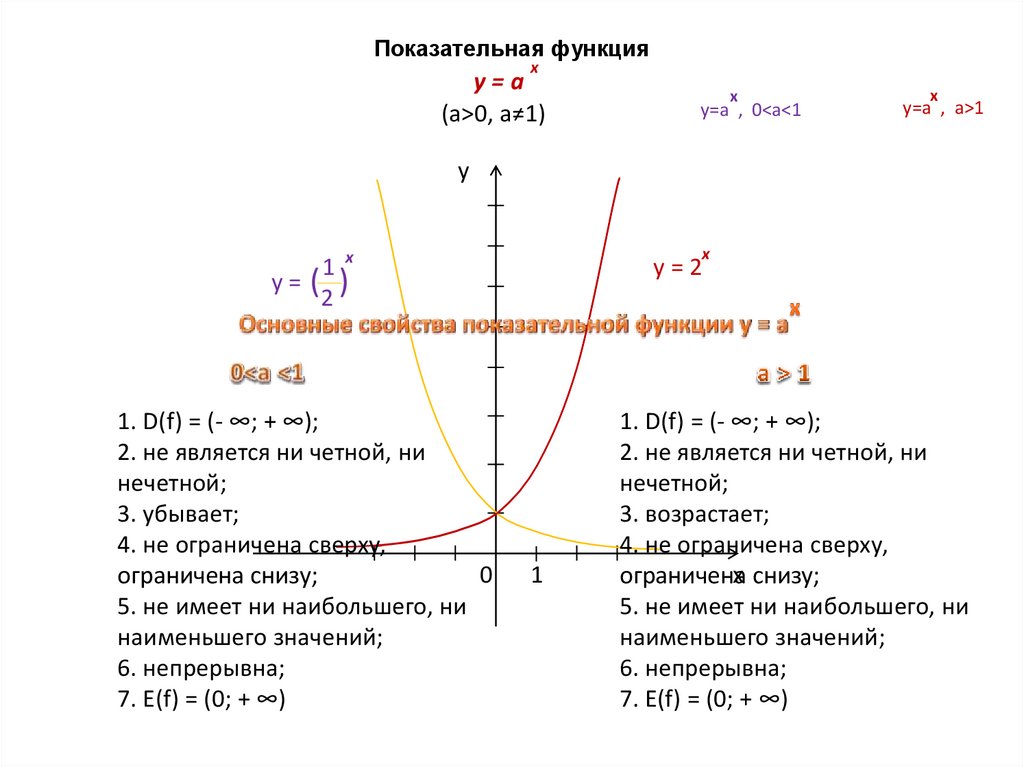
y=a , 0<a<1
x
y=a , a>1
y
x
1x
y= ( )
2
1. D(f) = (- ∞; + ∞);
2. не является ни четной, ни
нечетной;
3. убывает;
4. не ограничена сверху,
0
ограничена снизу;
5. не имеет ни наибольшего, ни
наименьшего значений;
6. непрерывна;
7. E(f) = (0; + ∞)
y=2
1
1. D(f) = (- ∞; + ∞);
2. не является ни четной, ни
нечетной;
3. возрастает;
4. не ограничена сверху,
x снизу;
ограничена
5. не имеет ни наибольшего, ни
наименьшего значений;
6. непрерывна;
7. E(f) = (0; + ∞)

9.

Показательная функция
x
y=a
(a>0, a≠1)
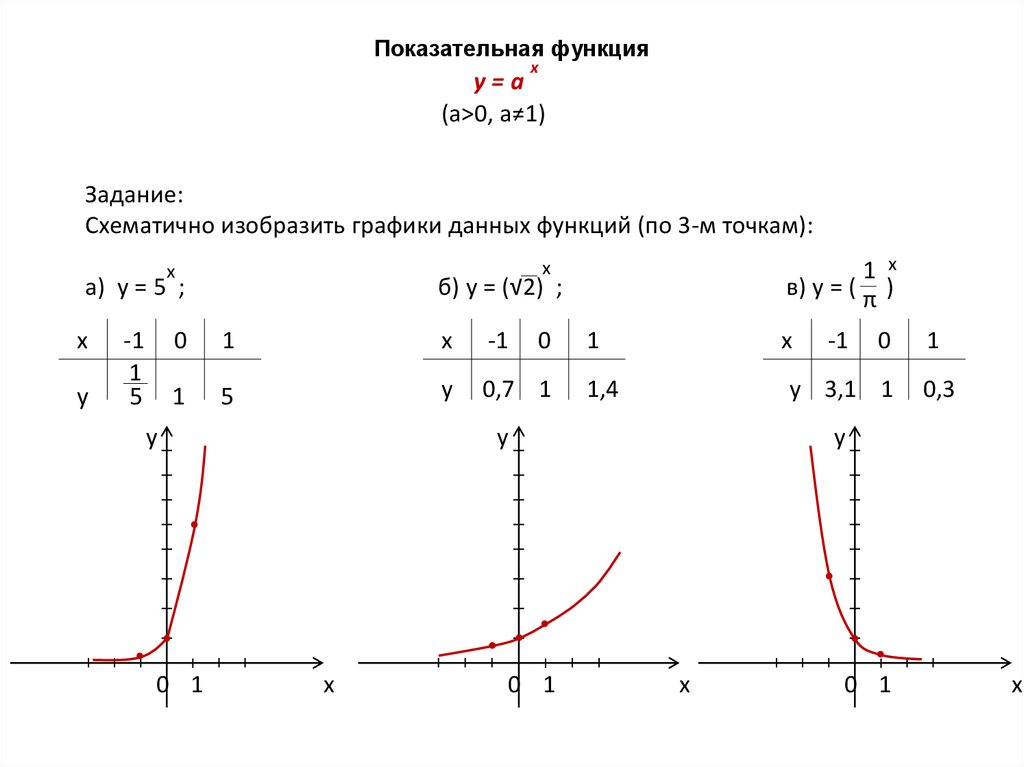
Задание:
Схематично изобразить графики данных функций (по 3-м точкам):
а) y = 5 ;
x
y
-1
1
5
б) y = (√2) ;
0
1
x
-1
1
5
y
0,7 1
y
0 1
1 x
в) y = ( π )
x
x
0
1
x
1,4
0 1
0
y 3,1 1
y
x
-1
1
0,3
y
x
0 1
x

10.

Решение задач в классе:
№ 192
№ 195