В чем смысл эквивалентности машин Тьюринга и Поста и нормальных алгоритмов Маркова?

1.

Государственное бюджетное общеобразовательное учреждение
СОШ № 17 Василеостровского района
В чем смысл эквивалентности машин
Тьюринга и Поста и нормальных алгоритмов
Маркова?
Выполнила:
Учитель информатики
Мардарь Надежда Петровна
г. Санкт – Петербург
2022г.

2.

То есть «конструктивно» машина Тьюринга, так же как и машина
Поста, состоит из двух основных узлов: ленты с ячейками и
каретки.
Тьюринг высказал предположение, что любой алгоритм в
интуитивном смысле этого слова может быть представлен
эквивалентной машиной в предложенной им модели вычислений.
Это предположение известно как тезис Черча—Тьюринга. Каждый
компьютер может моделировать машину Тьюринга, для этого
достаточно моделировать операции перезаписи ячеек, сравнения и
перехода к другой соседней ячейке с учетом изменения состояния
машины.
Значит, он может моделировать алгоритмы в машине Тьюринга, и
из этого тезиса следует, что все компьютеры, независимо от
мощности, архитектуры и других особенностей, с точки зрения
принципиальной возможности решения алгоритмически
разрешимых задач эквивалентны.

3.

Первые фундаментальные работы по теории алгоритмов были
опубликованы в середине 1930-х гг. Аланом Тьюрингом,
Алоизом Черчем и Эмилем Постом. Предложенные ими машина
Тьюринга, машина Поста и класс рекурсивно-вычислимых
функций Черча были первыми формальными описаниями
алгоритма, опирающимися на строго определенные модели
вычислений. Сформулированные гипотезы Поста и Черча—
Тьюринга постулировали эквивалентность предложенных ими
моделей вычислений, как формальных систем, и интуитивного
понятия алгоритма. Важным развитием этих работ стала
формулировка и доказательство существования алгоритмически
неразрешимых проблем.

4.

В
1950-х гг. существенный вклад в развитие
теории алгоритмов внесли работы Колмогорова и
основанный на теории формальных грамматик
алгоритмический формализм Маркова — так
называемые нормальные алгоритмы Маркова.
Формальные модели алгоритмов Поста, Тьюринга
и Черча, равно как и модели Колмогорова и
Маркова, оказались эквивалентными в том
смысле, что любой класс проблем, разрешимых в
одной модели, разрешим и в другой.

5.

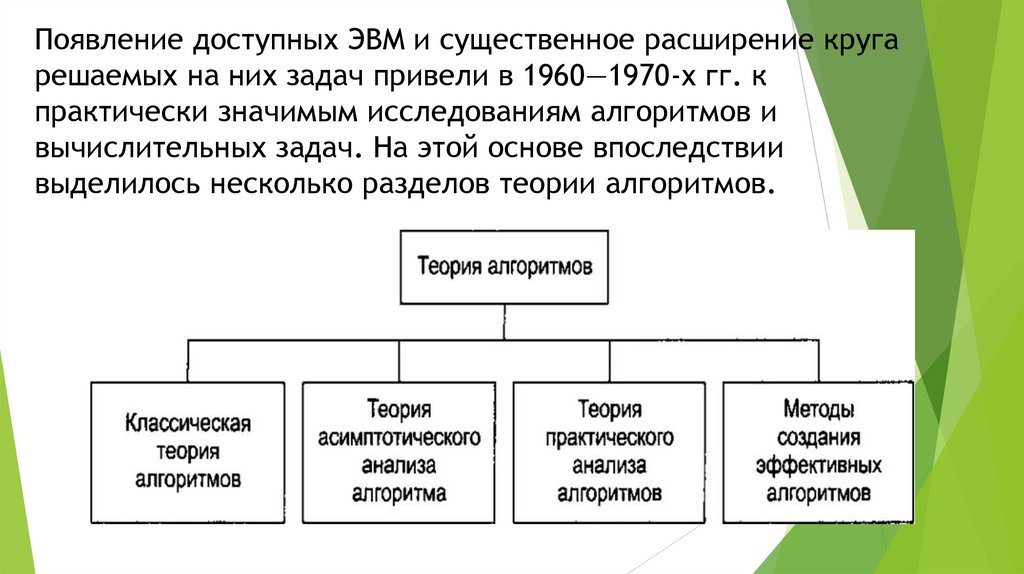
Появление доступных ЭВМ и существенное расширение круга
решаемых на них задач привели в 1960—1970-х гг. к
практически значимым исследованиям алгоритмов и
вычислительных задач. На этой основе впоследствии
выделилось несколько разделов теории алгоритмов.

6.

Классическая теория алгоритмов: формулировка задач в терминах формальных
языков; понятие задачи разрешения; описание сложностных классов задач; формулировка в 1965 г. Эдмондсом проблемы P = NP; открытие класса TVP-полных
задач и его исследование; введение новых моделей вычислений — алгебраического
дерева вычислений (Бен-Op), машины с произвольным доступом к памяти, схем
алгоритмов Янова, стандартных схем программ Котова и др.
Теория асимптотического анализа алгоритмов: понятие сложности и трудоемкости алгоритма; критерии оценки алгоритмов; методы получения асимптотических
оценок, в частности, для рекурсивных алгоритмов; асимптотический анализ
трудоемкости или времени выполнения; получение теоретических нижних оценок
сложности задач. В развитие этой теории внесли существенный вклад Кнут, Ахо,
Хопкрофт, Ульман, Карп, Мошков, Кудрявцев и др.
Теория практического анализа вычислительных алгоритмов: получение явных
функций трудоемкости; интервальный анализ функций; практически значимые
критерии качества алгоритмов; методики выбора рациональных алгоритмов. Основополагающей работой в этом направлении, очевидно, следует считать фундаментальный труд Д. Кнута «Искусство программирования для ЭВМ».
Методы создания эффективных алгоритмов включают в себя множество алгоритмов,
среди которых динамическое программирование, метод ветвей и границ, метод
декомпозиции, «жадные» алгоритмы, специальные структуры данных и пр.

7.

Обобщая исследования в различных разделах теории алгоритмов, можно выделить
следующие основные задачи и направления развития, характерные для современной
теории алгоритмов:
□ формализация понятия «алгоритм» и исследование формальных алгоритмических
систем (моделей вычислений);
□ доказательство алгоритмической неразрешимости задач;
□ формальное доказательство правильности и эквивалентности алгоритмов;
□ классификации задач, определение и исследование сложностных классов;
□ доказательство теоретических нижних оценок сложности задач;
□ получение методов разработки эффективных алгоритмов;
□ асимптотический анализ сложности итерационных алгоритмов;
□ исследование и анализ рекурсивных алгоритмов;
□ получение явных функций трудоемкости алгоритмов;
□ разработка классификаций алгоритмов;
□ исследование емкостной (по ресурсу памяти) сложности задач и алгоритмов;
□ разработка критериев сравнительной оценки ресурсной эффективности алгоритмов
и методов их сравнительного анализа.