Similar presentations:
Формализация понятия алгоритма Машина Тьюринга. Функции, вычислимые по Тьюрингу
1.
Формализация понятия алгоритмаМашина Тьюринга
Функции, вычислимые по Тьюрингу
Кольчугин Иван 10И4
2.
Оглавление• Формализация понятия алгоритма (что это такое, зачем нужно, кто развил)
• Машина Тьюринга и ее компоненты (что это такое, принцип работы, основные
компонент)
• Функции, вычислимые по Тьюрингу (типы функций, которые можно вычислить на
машине Тьюринга)
• Примеры
3.
Формализацияпонятия алгоритма
Формализация понятия алгоритма – это процесс
представления алгоритма с использованием формальных
языков и методов. Позволяет четко и однозначно описать
шаги, необходимые для решения задачи.
Для этого может используется псевдокод, блок-схемы или
специализированные языки
программирования. Формализация позволяет
разработчикам исключить неоднозначности и обеспечить
ясность в описании шагов, необходимых для решения
задачи.
Наибольший вклад в это направление внесли Алан Тьюринг и
Алонзо Черч.
4.
Машина Тьюринга• Машина Тьюринга – это математическая модель вычислений, предложенная
Аланом Тьюрингом в 1936г. Она является абстрактным устройством,
предназначенным для формализации понятия алгоритма и исследования
пределов вычислительной мощности.
• Существует тезис Тьюринга , что утверждает, что если задача может быть
эффективно решена на Машине Тьюринга, то она может быть решена эффективно
и на любом другом устройстве, способном эффективно реализовать
вычислительные функции
5.
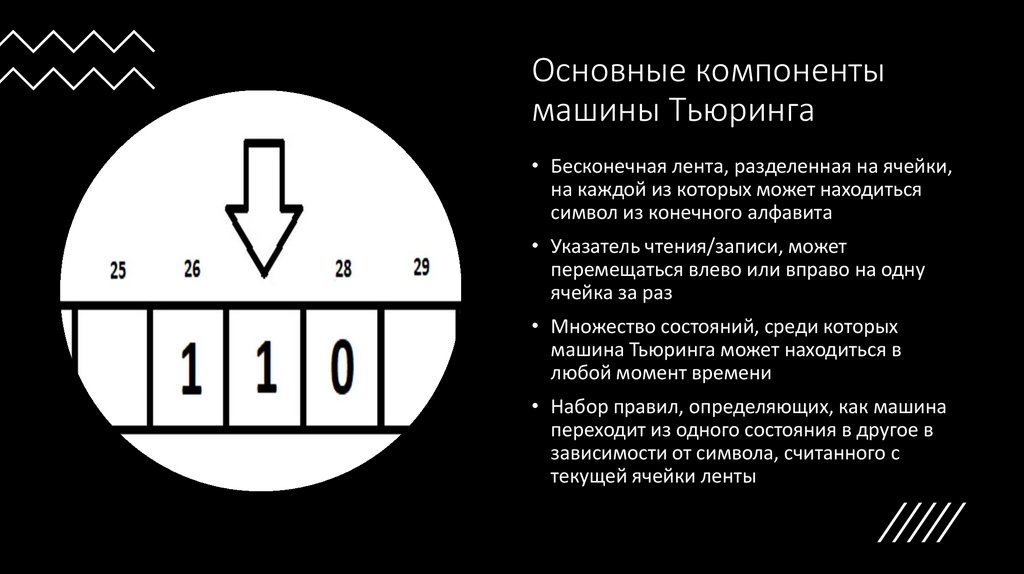
Основные компонентымашины Тьюринга
• Бесконечная лента, разделенная на ячейки,
на каждой из которых может находиться
символ из конечного алфавита
• Указатель чтения/записи, может
перемещаться влево или вправо на одну
ячейка за раз
• Множество состояний, среди которых
машина Тьюринга может находиться в
любой момент времени
• Набор правил, определяющих, как машина
переходит из одного состояния в другое в
зависимости от символа, считанного с
текущей ячейки ленты
6.
Функции, вычислимые по Тьюрингу• Арифметические функции – сложение, вычитание, умножение, деление и т.п.
• Логический функции – конъюнкция, дизъюнкция, инверсия, равенство,
неравенство и т.п.
• Функции, связанные с последовательностями – работа с массивами, строками и
другими структурами данных
• Условные операторы – if-then-else
• Рекурсивные функции – использование рекурсии
• Цикличные функции – циклы и итерации
7.
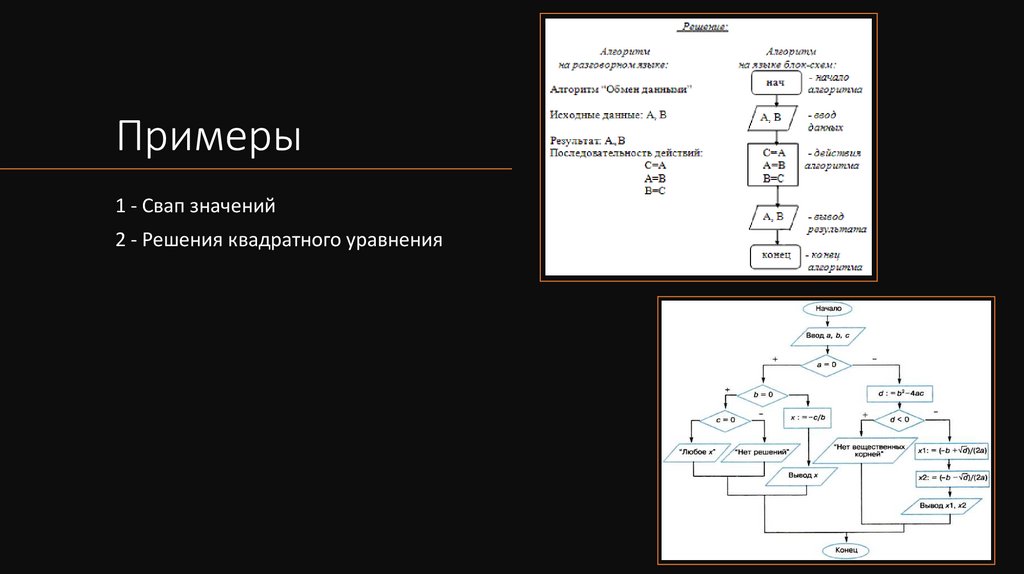
Примеры1 - Свап значений
2 - Решения квадратного уравнения





 informatics
informatics








