Similar presentations:
Число, положение и комбинация
1.
Число, положение и комбинация 0011 0010 1010 1101 0001 0100 1011три взаимно пересекающиеся,
но различные сферы мысли,
к которым можно отнести
все математические идеи.
1
Джеймс Джозеф Сильвестр
(1814-1897)
английский математик
2
4
2. Выбираем с умом
0011 0010 1010 1101 0001 0100 10111
2
4
Лосева Екатерина Анатольевна
учитель математики
ГБОУ школа №275
3.
ОбразноеЛогическое
0011 0010 1010 1101 0001 0100 1011
Мышление
Комбинаторное
2
Интуитивное
1
4
Практическое
4. Задача о бесплатном обеде
0011 0010 1010 1101 0001 0100 10111
2
4
5.
Рассадкаповторится через
0011 0010 1010 1101 0001 0100 1011
10 000 лет
1
2
4
6. Комбинаторика
__________это
область
математики,
0011 0010 1010 1101 0001 0100 1011
в которой изучаются вопросы о
__________
том, сколько различных комбинаций,
подчиненных тем или иным
условиям, можно составить из
__________
элементов, принадлежащих
заданному множеству.
1
2
4
7.
Пробуемкомбинировать
0011 0010 1010 1101 0001 0100 1011
1
2
4
8.
Признакиотличия выборок
0011 0010 1010 1101 0001 0100 1011
Все элементы
Не все
элементы
Порядок
имеет
значение
Размещение
Порядок не
имеет
значения
Сочетание
1
2
4
Порядок
имеет
значение
Перестановка
9. Важен порядок или нет:
а) при выборе капитанаволейбольной команды и его
заместителей;
б) три ноты в аккорде;
в) шесть человек останутся
убирать класс;
г) 2 серии нового
многосерийного фильма.
0011 0010 1010 1101 0001 0100 1011
1
2
4
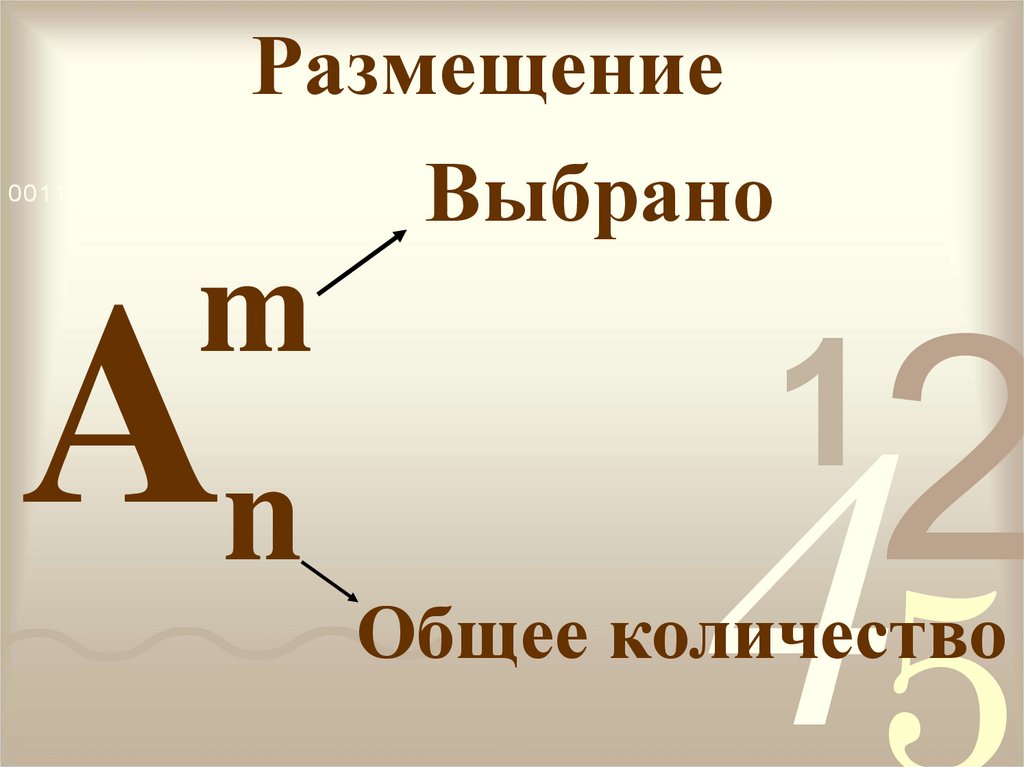
10. Размещение
Выбрано0011 0010 1010 1101 0001 0100 1011
m
An
1
2
4
Общее количество
11. Перестановка
0011 0010 1010 1101 0001 0100 1011Pn
1
2
4
Общее количество
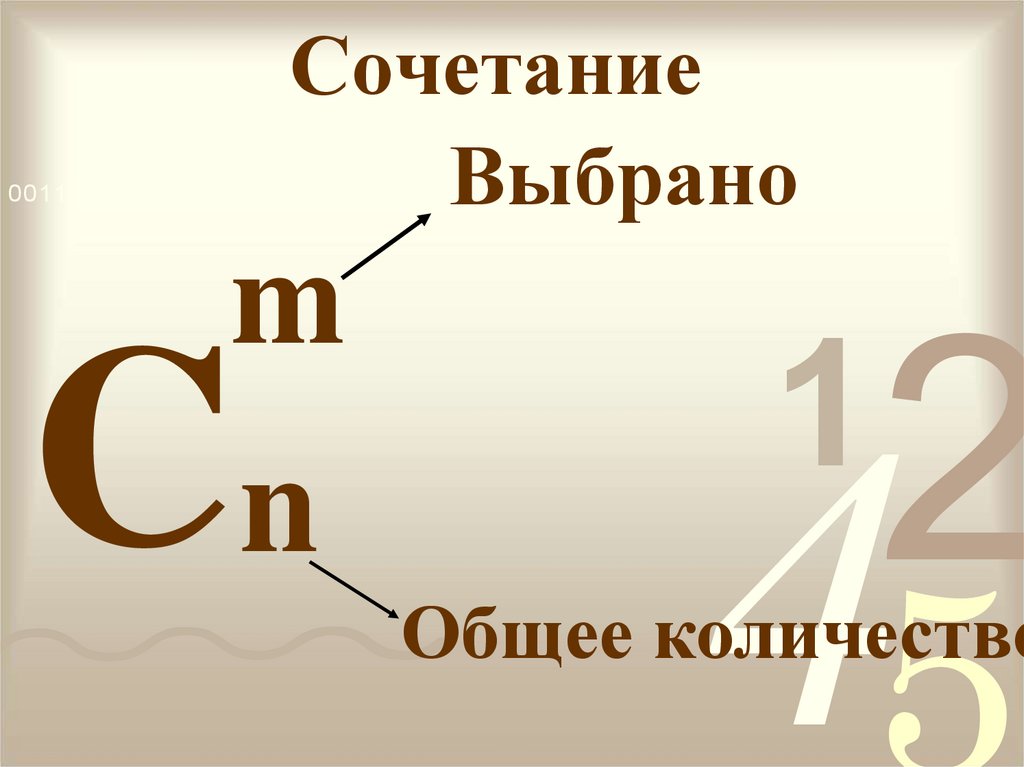
12. Сочетание
Выбрано0011 0010 1010 1101 0001 0100 1011
m
Cn
1
2
4
Общее количество
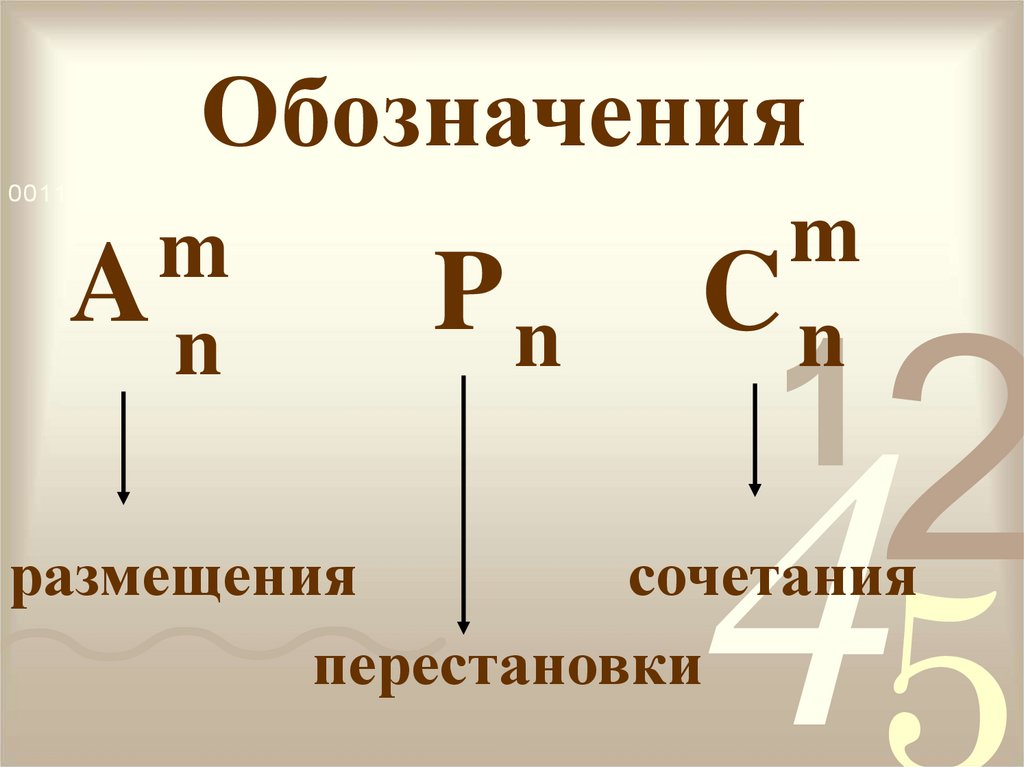
13.
Обозначения0011 0010 1010 1101 0001 0100 1011
m
An
Pn
m
Cn
1
2
4
размещения
сочетания
перестановки
14. Вывод формул
0011 0010 1010 1101 0001 0100 10113
A 5 =5 ∙(5-1)∙(5-2)=5 ∙4 ∙3
m
=n
∙
(n-1)
∙
(n-2)
∙
…
∙
(n-(m-1))
An
1
2
4
15. Факториал
0011 0010 1010 1101 0001 0100 1011n!= 1∙2∙3 ∙…∙n
5!=1∙2∙3∙4∙5=120
4!=1∙2∙3∙4=24
0!=1
1
2
4
16.
mn!
1) А =
(n-m)!
n
0011 0010 1010 1101 0001 0100 1011
2)
Pn = n!
n!
m
3) C =
n (n-m)! m!
1
2
4
17. Задача о бесплатном обеде
0011 0010 1010 1101 0001 0100 10111
2
4
18. Задача о бесплатном обеде
0011 0010 1010 1101 0001 0100 1011P = 1∙2∙3∙4∙5∙6∙7∙8∙9∙10=
10
=3628800
1
2
4
19. Алгоритм решения
0011 0010 1010 1101 0001 0100 1011Тип выборки
Формула
Применение формулы к данным задачи
Запись ответа
1
2
4
20. Задача
В группе кандидатов на первыйполет в космос были шесть
летчиков: Варламов, Гагарин,
Карташов, Николаев, Попович и
Титов. Сколько было способов
выбрать основного претендента
на полет, первого дублера и
второго дублера?
0011 0010 1010 1101 0001 0100 1011
1
2
4
21. Алгоритм решения
0011 0010 1010 1101 0001 0100 1011Тип выборки
Формула
Применение формулы к данным задачи
Запись ответа
1
2
4
22. Решение:
0011 0010 1010 1101 0001 0100 10113
A
6
=
6!
(6-3)!
1∙2∙3∙4∙5∙6
=
=120
1∙2∙3
1
2
4
Ответ: 120 способов.
23.
mn!
1) А =
(n-m)!
n
0011 0010 1010 1101 0001 0100 1011
2)
Pn = n!
n!
m
3) C n =
(n-m)! m!
1
2
4
24. Алгоритм решения
0011 0010 1010 1101 0001 0100 1011Тип выборки
Формула
Применение формулы к данным задачи
Запись ответа
1
2
4
25. Ответы
0011 0010 1010 1101 0001 0100 1011а) 720
б) 24
в) 70
1
2
4
26. Решение:
0011 0010 1010 1101 0001 0100 10113
А
10
=
10!
(10-3)!
Ответ: 720 способов.
1
2
4
27. Решение:
0011 0010 1010 1101 0001 0100 1011Р4 = 1∙2∙3∙4=24
Ответ: 24 способа.
1
2
4
28. Решение:
0011 0010 1010 1101 0001 0100 10111∙2∙3∙4∙5∙6∙7 ∙8
=
=
=70
(8-4)!∙4! 1∙2∙3∙4∙1∙2 ∙3∙4
8
4
С
8!
Ответ: 70 способов.
1
2
4
29.
0011 0010 1010 1101 0001 0100 1011Цифры (числа)
не управляют миром,
но они показывают,
как управляется мир.
(И. Гете)
1
2
4











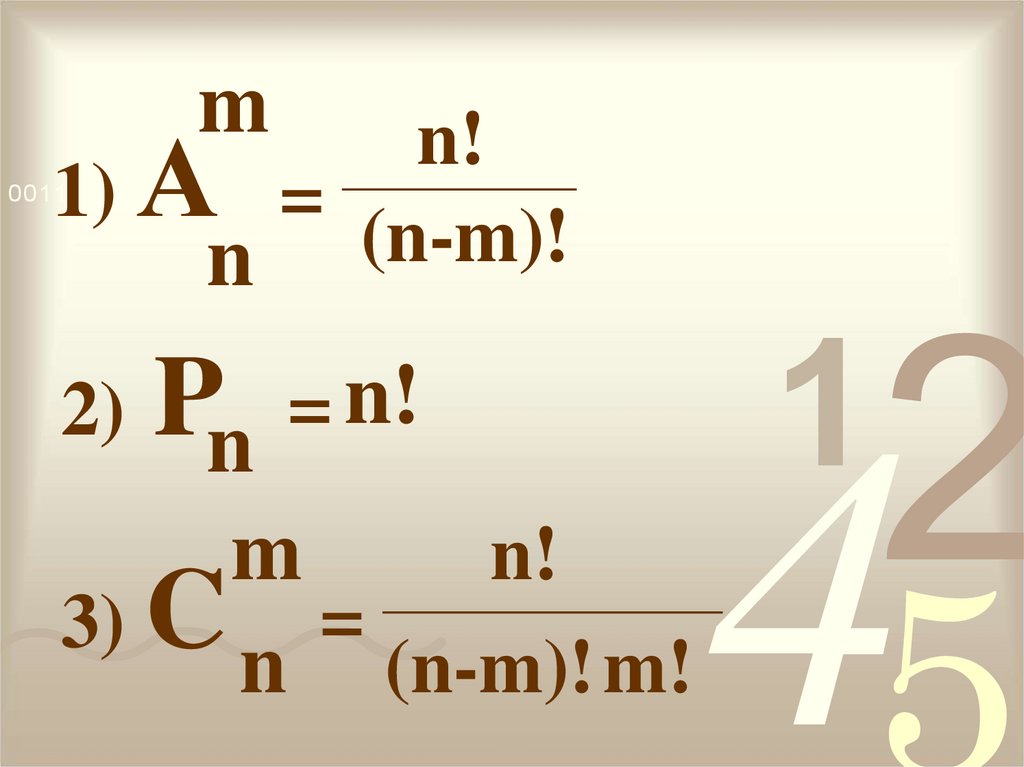













 mathematics
mathematics








