Similar presentations:
Признаки равенства треугольников
1.
ГеометрияПризнаки равенства
треугольников
Выполнила: учитель математики ГБОУ СОШ № 538
г Санкт-Петербург
Шумилова Татьяна Вячеславовна
2.
ТреугольникТреугольник - это фигура на плоскости, состоящая из трех точек, не
лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами, а отрезки — сторонами треугольника.
A
Вершины треугольника:
Всегда называют одной заглавной латинской буквой
C; B; A
Углы треугольника:
Всегда называют тремя заглавными латинскими буквами
∠CAB; ∠ABC; ∠BCA
Стороны треугольника:
Всегда называют двумя заглавными латинскими
буквами CA; AB; BC
C
B
3.
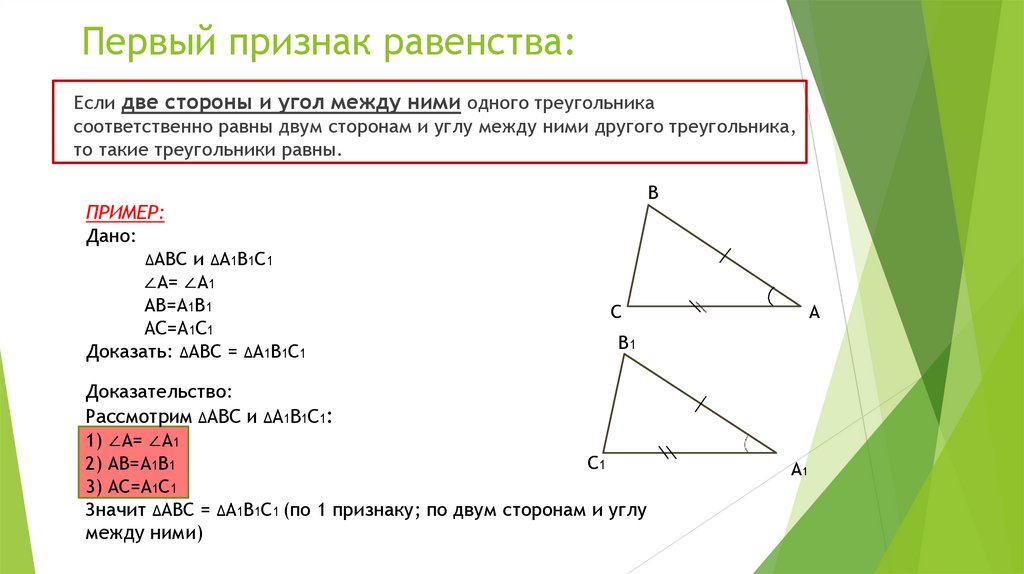
Первый признак равенства:Если две стороны и угол между ними одного треугольника
соответственно равны двум сторонам и углу между ними другого треугольника,
то такие треугольники равны.
ПРИМЕР:
Дано:
ΔABC и ΔA1B1C1
∠A= ∠A1
AB=A1B1
AC=A1C1
Доказать: ΔABC = ΔA1B1C1
B
C
A
B1
Доказательство:
Рассмотрим ΔABC и ΔA1B1C1:
1) ∠A= ∠A1
C1
2) AB=A1B1
3) AC=A1C1
Значит ΔABC = ΔA1B1C1 (по 1 признаку; по двум сторонам и углу
между ними)
A1
4.
Задачи№93 Отрезки АЕ и DC пересекаются в точке В, являющейся серединой каждого из них.
а) Докажите, что треугольники АВС и EBD равны;
б) найдите углы А и С треугольника АВС, если в треугольнике BDE ∠D = 47°, ∠E = 42°
А
С
B
D
Так как ΔABC= ΔDBE, то
∠D=∠С
∠E= ∠A
Значит ∠D=∠С=47°
∠E= ∠A=42°
Ответ:∠A= 42°; ∠С= 47°
Е
Рассмотрим ΔABC и ΔDBE:
1) Проведем отрезки AC и DE
2)AB=BE
3)CB=BD
4) ∠ABC= ∠DBE(вертикальные углы)
5)Значит ΔABC= ΔDBE(по двум сторонам и углу
между ними)
5.
Второй признак равенства:Если сторона и два прилежащих к ней угла одного треугольника
соответственно равны стороне и двум прилежащим к ней углам другого
треугольника, то такие треугольники равны.
ПРИМЕР:
Дано: ΔABC и ΔA1B1C1
∠A= ∠A1
∠С= ∠С1
AC=A1C1
Доказать: ΔABC = ΔA1B1C1
B
C
Доказательство:
Рассмотрим ΔABC и ΔA1B1C1:
1) ∠A= ∠A1
2) ∠С= ∠С1
3) AC=A1C1
Значит ΔABC = ΔA1B1C1 (по 2 признаку; по стороне и двум
прилежащим к ней углам)
A
B1
C1
A1
6.
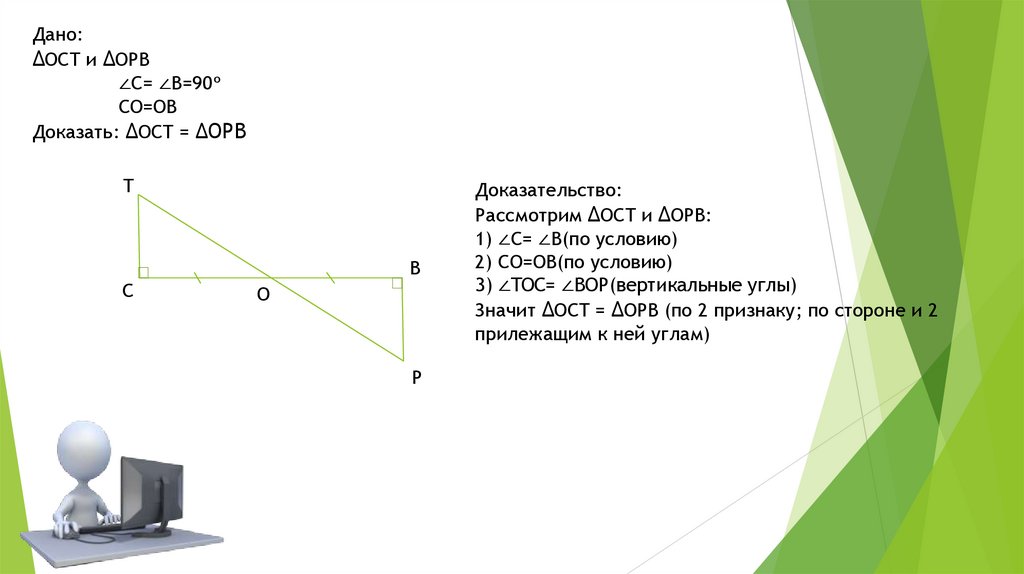
Дано:ΔOCT и ΔOPB
∠C= ∠B=90°
CO=OB
Доказать: ΔOCT = ΔOPB
T
B
C
O
P
Доказательство:
Рассмотрим ΔOCT и ΔOPB:
1) ∠C= ∠B(по условию)
2) CO=OB(по условию)
3) ∠TOC= ∠BOP(вертикальные углы)
Значит ΔOCT = ΔOPB (по 2 признаку; по стороне и 2
прилежащим к ней углам)
7.
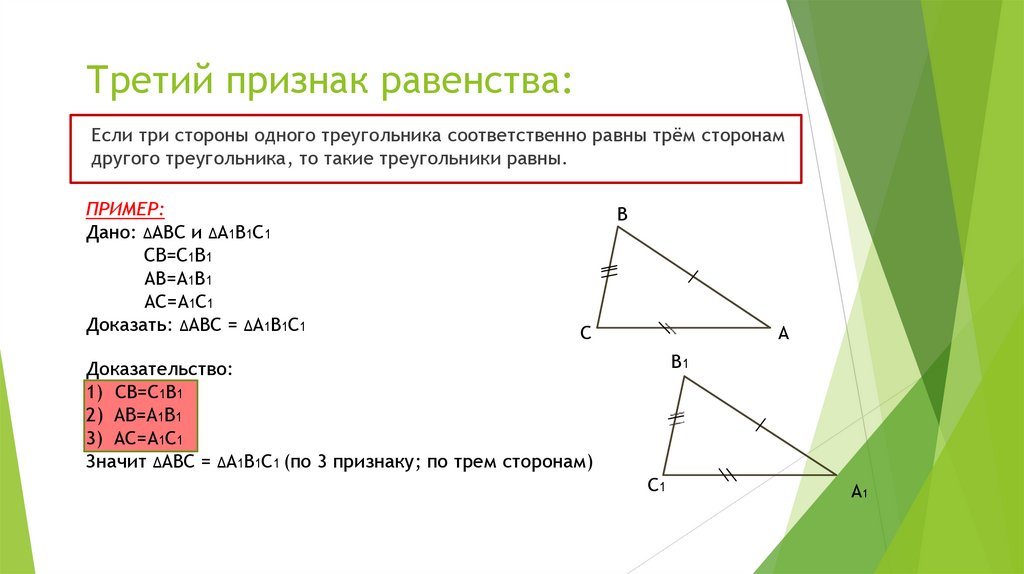
Третий признак равенства:Если три стороны одного треугольника соответственно равны трём сторонам
другого треугольника, то такие треугольники равны.
ПРИМЕР:
Дано: ΔABC и ΔA1B1C1
СB=С1B1
AB=A1B1
AC=A1C1
Доказать: ΔABC = ΔA1B1C1
B
C
A
B1
Доказательство:
1) СB=С1B1
2) AB=A1B1
3) AC=A1C1
Значит ΔABC = ΔA1B1C1 (по 3 признаку; по трем сторонам)
C1
A1
8.
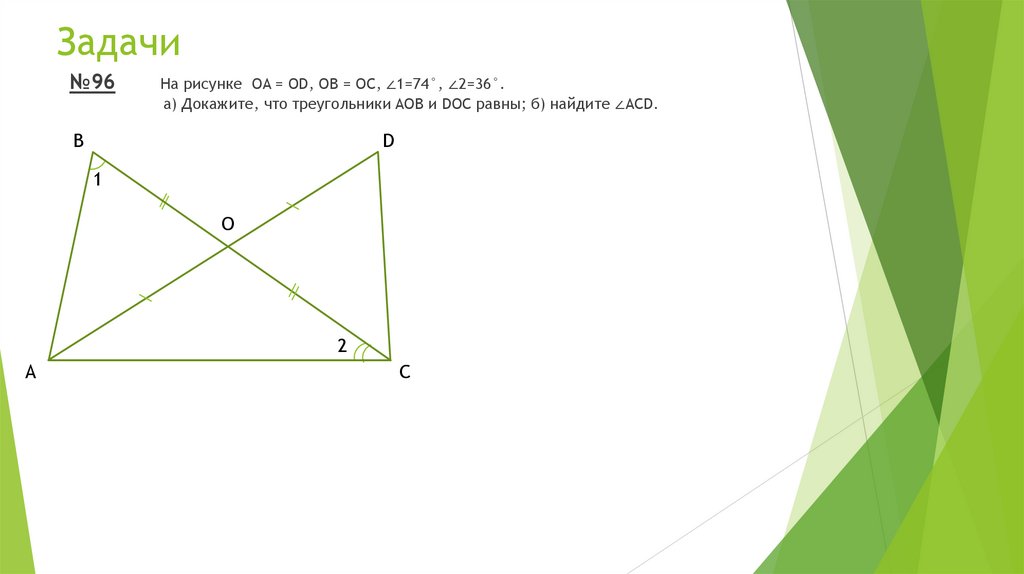
Задачи№96
На рисунке OA = OD, OB = ОС, ∠1=74°, ∠2=36°.
а) Докажите, что треугольники AOB и DOC равны; б) найдите ∠ACD.
B
D
1
О
2
А
С
9.
Задачи№94
На рисунке 52 AB=АС, ∠1=∠2. а) Докажите, что треугольники ABD и ACD равны;
б) найдите BD и AB, если АС = 15 см, DC = 5 см.
B
А
1
D
2
С
10.
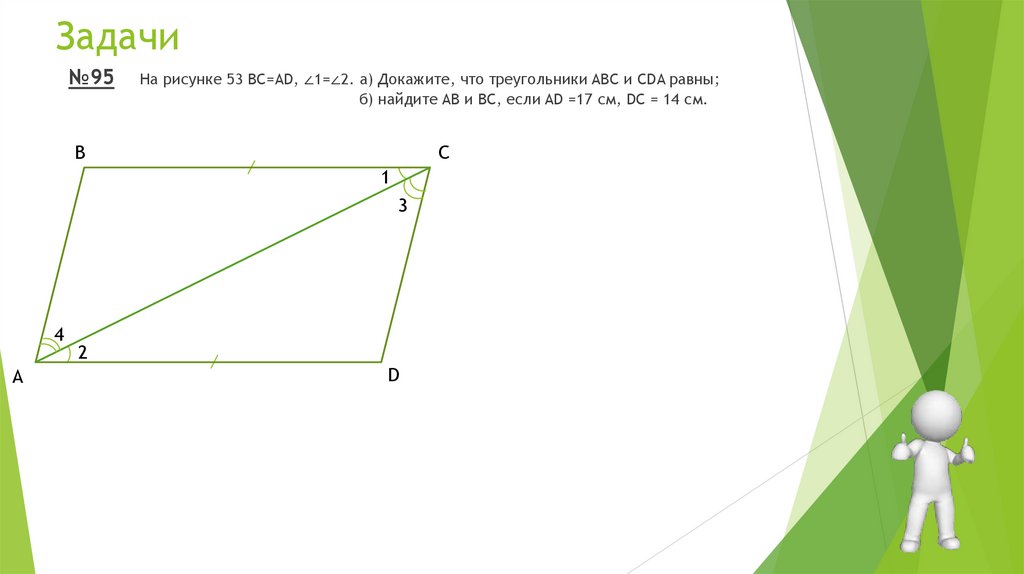
Задачи№95
На рисунке 53 BC=AD, ∠1=∠2. а) Докажите, что треугольники ABC и CDA равны;
б) найдите AB и BC, если AD =17 см, DC = 14 см.
B
С
1
3
4
А
2
D





 mathematics
mathematics








