Относительная частота и закон больших чисел

1.

Относительная частота
и закон больших чисел.

2.

Какое из перечисленных
событий достоверное?
1. Вода в реке Обь закипит.
2. Круглая отличница получит двойку.
3. В году найдется месяц, в котором
будет пять воскресений.

3.

Какое из перечисленных
событий невозможно?
1. В 12 часов ночи в Яланском идет
дождь, а через 24 часа будет
светить солнце.
2. Сорванный цветок завянет.
3. Если до воздушного шарика
дотронуться иглой, то он лопнет.

4.

Какое из данных событий
случайное?
1. Ударом молотка можно разбить
стекло.
2. Воробей научится говорить.
3. Завтра будет хорошая погода.

5.

Задача 1. На школьной олимпиаде по
математике было предложено 5 заданий,
Алеша выполнил 3,5 задания,
а Игорь – 2 задания.
У кого больше шансов стать
победителем на школьной олимпиаде?
1. У Алеши.
2. У Игоря.

6.

Задача 2. Бросили 100 раз игральный кубик. При
бросании игрального куба на его верхней грани
кубика выпадают очки:
И с х о д ы и с п ы т а н и я:
1. Выпадает одно очко.
2. Выпадает два очка.
3. Выпадает три очка.
4. Выпадает четыре очка.
5. Выпадает пять очков.
6. Выпадает шесть очков.
• С л у ч а й н о е с о б ы т и е:
- выпадет шесть очков.
• Ч а с т о т а с о б ы т и я:
- в данной серии экспериментов «шестёрка»
выпала 17 раз.
Относительная
частота
- отношение частоты к общему числу испытаний.
(в нашем случае 17 / 100 )

7.

Относительной частотой события А называют
отношение числа испытаний М, в которых это
событие произошло, к числу всех проведенных
испытаний N. При этом число М называют частотой
события А
W(A)-относительная частота события А
M
W(A)
N
Под статистической вероятностью понимают число,
около которого колеблется относительная частота
события при большом числе испытаний

8.

Почему важна относительная
частота события?
Приведем пример.
Иван попал в мишень три раза, Петр – четыре.
Кто из них лучше стреляет?
Можно ответить, что Петр – лучше, так как больше число
попаданий. Но мы не знаем, сколько у каждого было
попыток. Например, Иван сделал всего три выстрела и
попал все три раза, относительная частота попадания
W(A) = M / N = 1.
А Петр сделал серию из 20 выстрелов и попал всего четыре
раза: W(A) = M / N = 0,2.)

9.

Во время тренировки в стрельбе по цели было сделано
30 выстрелов и зарегистрировано 26 попаданий.
Какова относительная частота попаданий по цели в
данной серии выстрелов?
Событие А- «попадание по цели» произошло в 26 случаях
Общее число испытаний N=30
26 13
W
30 15

10.

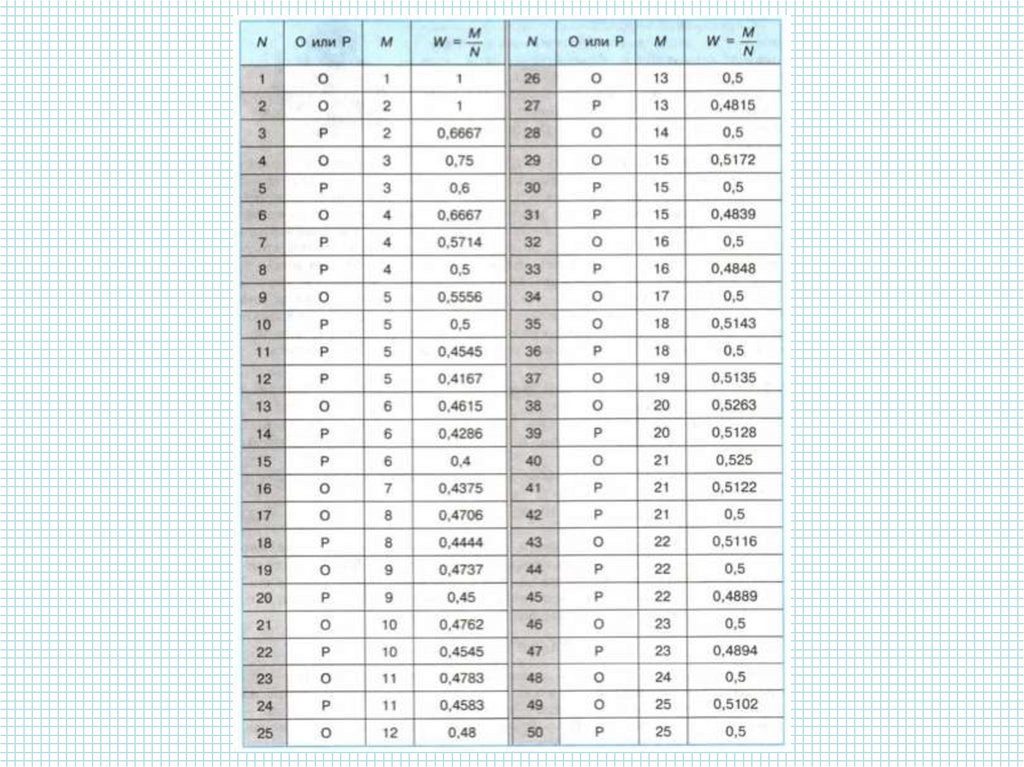
Задача
Исследование. Два друга проводили
испытания (опыты) с подбрасыванием
монеты и наблюдали за появлением
орла. Один из мальчиков подбрасывал
монету и сообщал о том, что выпало –
орел (О) или решка (Р). Второй мальчик
вносил результаты испытаний во второй
столбец таблицы:

11.

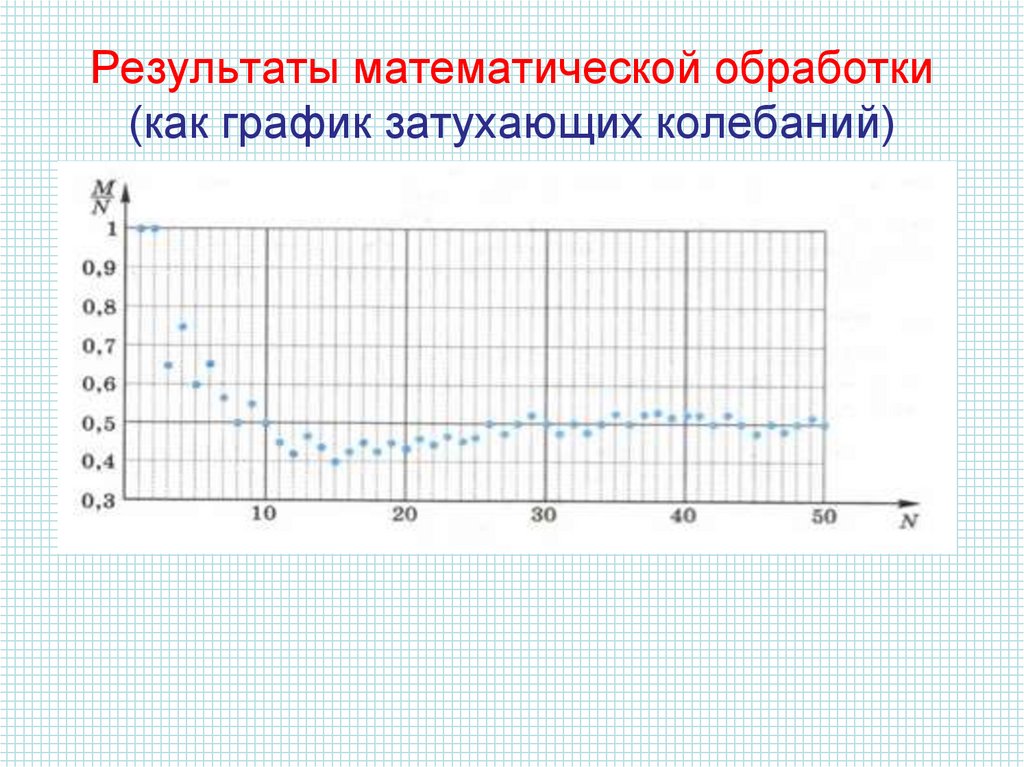
12.

Результаты математической обработки
(как график затухающих колебаний)

13.

Вычислим вероятность появления
орла (событие А)
при подбрасывании монеты
Р (А) = m / n
Число всех равновозможных исходов
n = 2 (О или Р)
Событию А благоприятствует 1 исход:
m = 1 ( О)
Р (А) = m / n = 1 / 2 = 0,5

14.

Закон больших чисел
Можно считать достоверным тот факт,
что при большом числе испытаний
относительная частота события W (A)
практически не отличается от его
вероятности Р (А), т.е.
Р (A) ≈ W (А)
при большом числе испытаний.

15.

Провел 4040 испытаний с
подбрасыванием монеты
Орел-2048 раз
2048
W
0,5069
4040
Французский естествоиспытатель
Жорж Луи Леклерк де Бюффон
(1707-1788)

16.

Провел 24 000 испытаний
с подбрасыванием монеты
Орел – 12 012 раз
12012
W
0,5005
24000
Карл Пирсон
(1857-1936)
английский ученый

17.

При большом числе испытаний
относительная частота события
W(A) практически не отличается
от его вероятности Р(А).
W(A) ≈ P(A)
Якоб Бернулли (1654-1705)
швейцарский математик
обосновал закон больших чисел

18.

Родильный дом некоторого города вел по годам подсчет рождения
мальчиков и девочек. Результаты заносились в таблицу. Найти
относительную частоту рождения мальчиков в данный период.
Год
Число родившихся детей
Девочки
Мальчики
1998
1999
2000
802
629
714
823
665
769
2001
2002
756
783
798
811
823+665+769+798+811=3866 - мальчиков
3684+802+629+714+756+783= 7550-всего детей
3866
W
0,5121
7550

19.

№
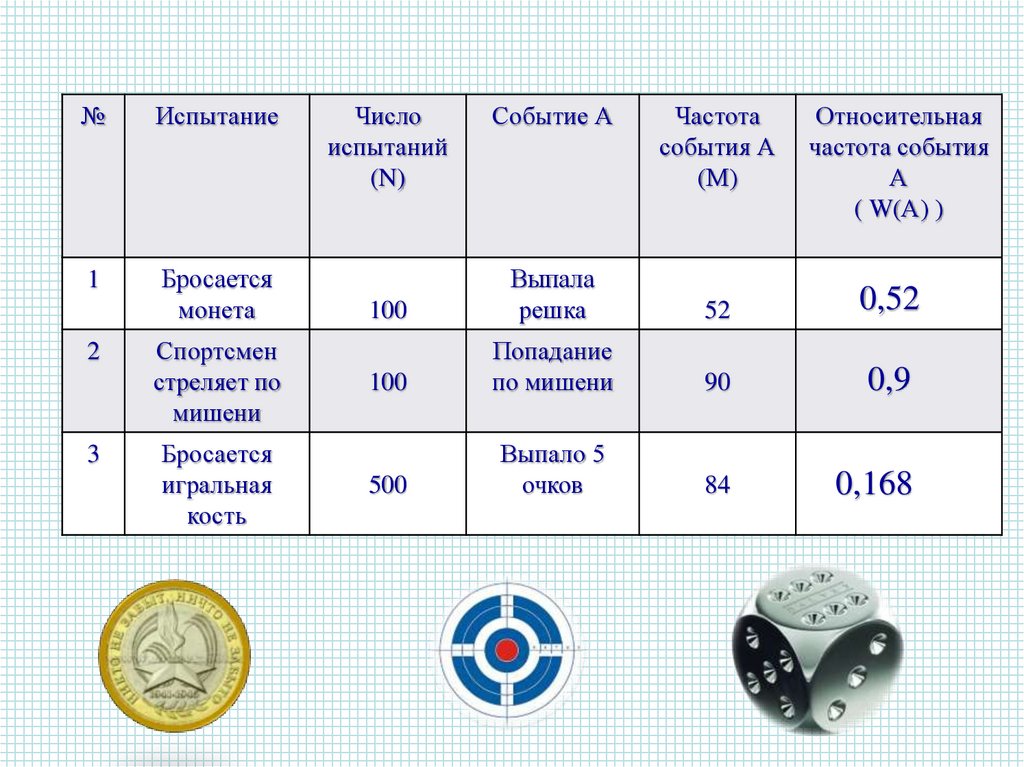
Испытание
1
Бросается
монета
2
3
Спортсмен
стреляет по
мишени
Бросается
игральная
кость
Число
испытаний
(N)
Событие А
Частота
события А
(М)
Относительная
частота события
А
( W(А) )
100
Выпала
решка
52
0,52
100
Попадание
по мишени
90
0,9
500
Выпало 5
очков
84
0,168

20.

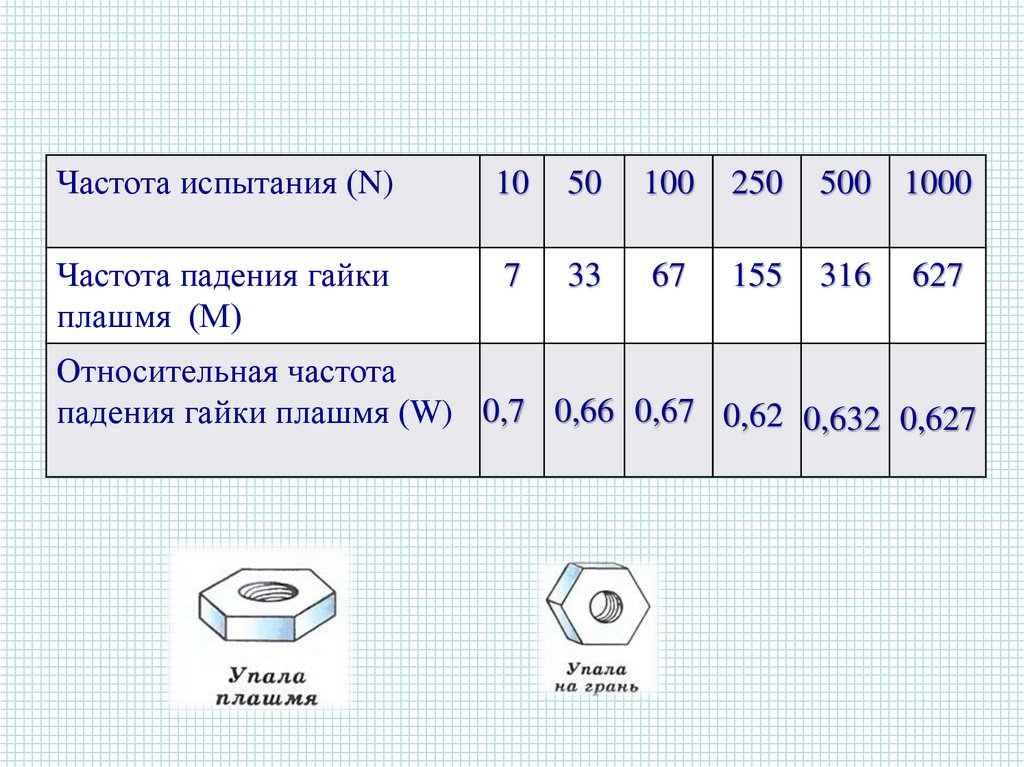
Частота испытания (N)
10
50
100
250
500 1000
Частота падения гайки
плашмя (М)
7
33
67
155
316
627
Относительная частота
падения гайки плашмя (W) 0,7 0,66 0,67 0,62 0,632 0,627

21.

Частота испытания (N)
100
200
500
1000
Частота падения на бок (М1)
83
169
421
839
Частота падения на большой
круг (М2)
15
28
72
141
Относительная частота
падения на бок (W1)
Относительная частота
падения на бок (W2)
0,83
0,845 0,842 0,839
0,15
0,14 0,144 0,141

22.

Домашнее задание