Similar presentations:
Граф - набор вершин и связей между ними, называющихся рёбрами
1.
Задание 42.
Граф – это набор вершин и связеймежду ними, называющихся
рёбрами:
Граф, отображающий дороги между поселками
3.
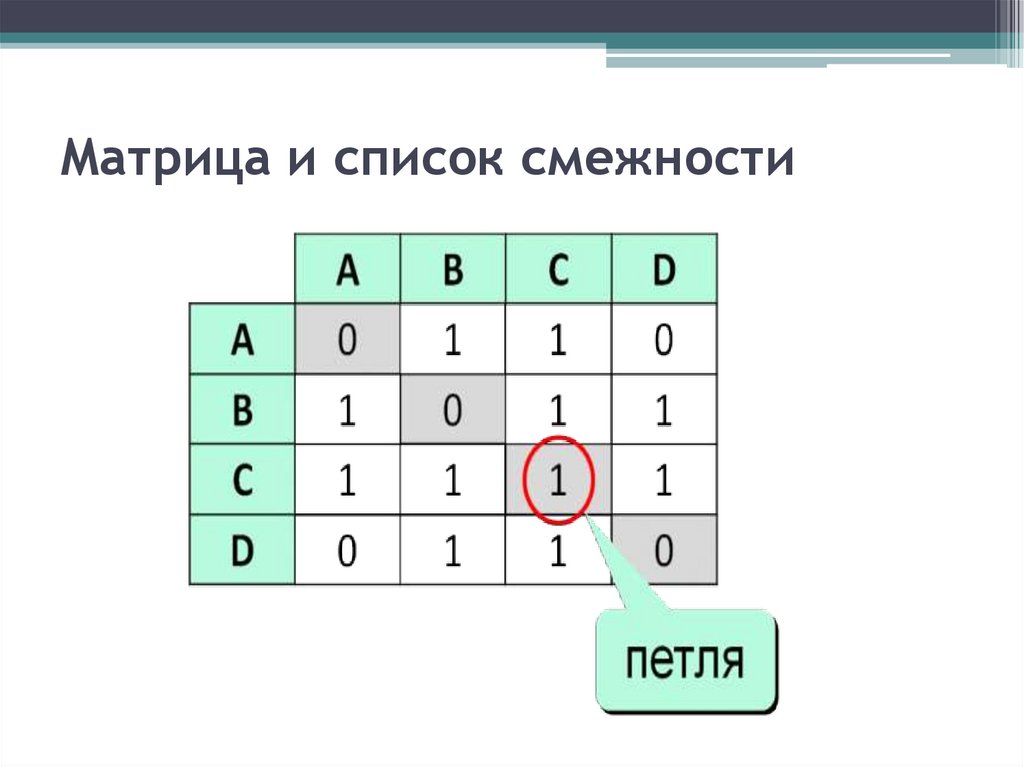
Матрица и список смежности4.
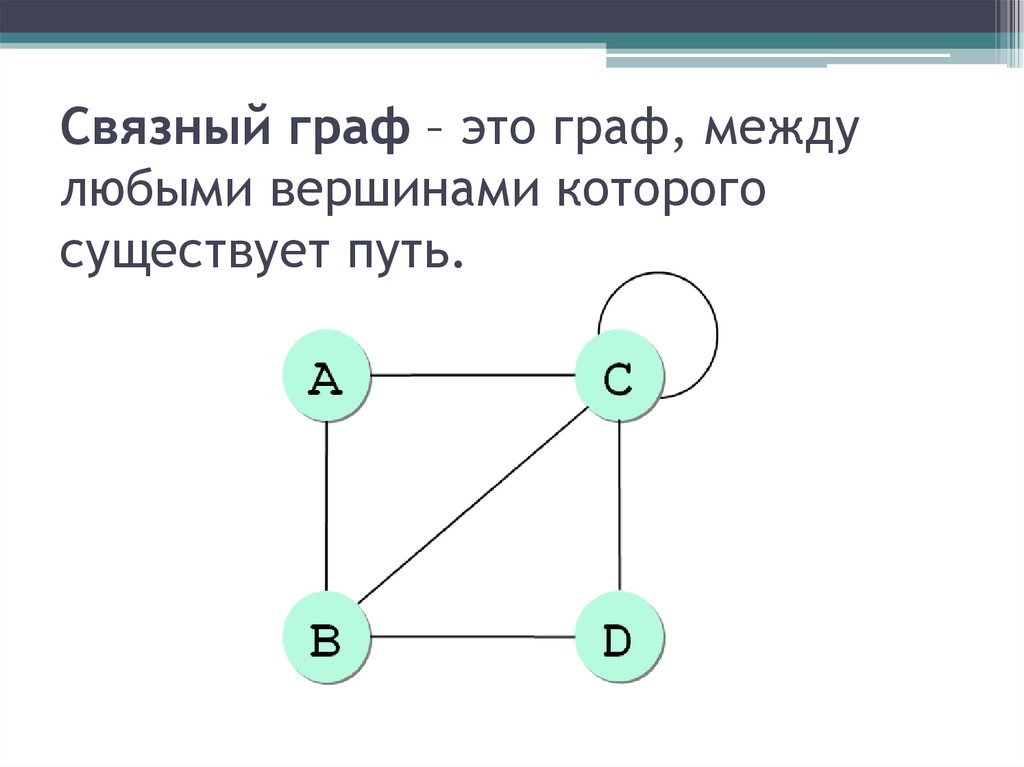
Связный граф – это граф, междулюбыми вершинами которого
существует путь.
5.
Дерево – это связный граф безциклов (замкнутых участков).
6.
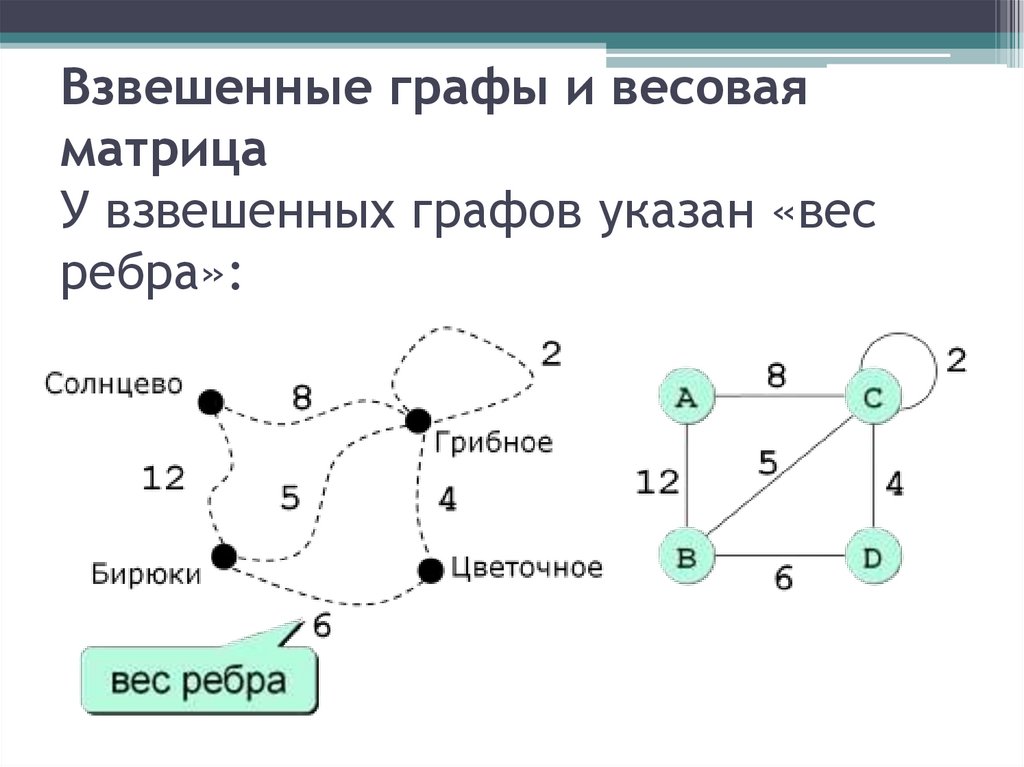
Взвешенные графы и весоваяматрица
У взвешенных графов указан «вес
ребра»:
7.
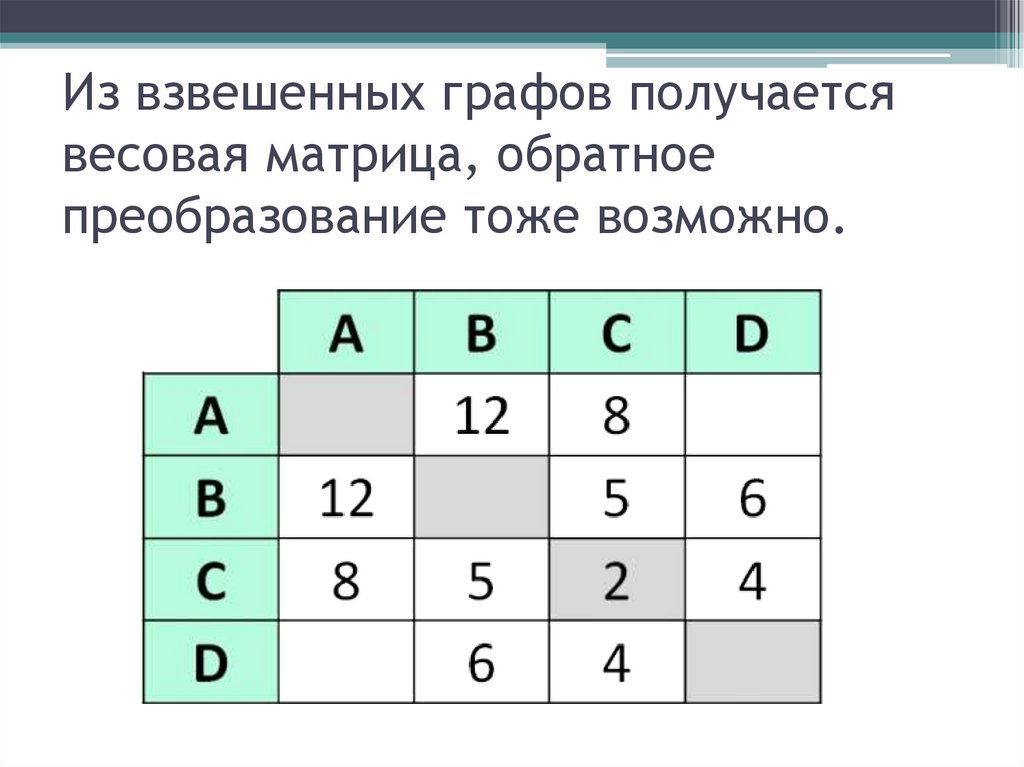
Из взвешенных графов получаетсявесовая матрица, обратное
преобразование тоже возможно.
8.
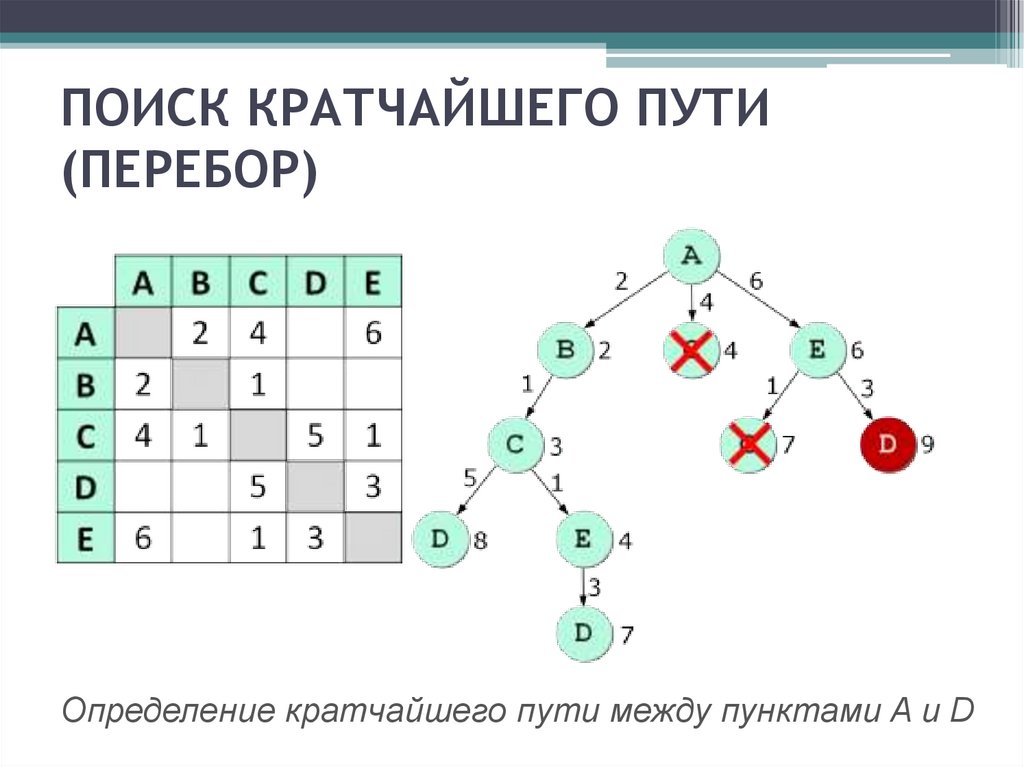
ПОИСК КРАТЧАЙШЕГО ПУТИ(ПЕРЕБОР)
Определение кратчайшего пути между пунктами A и D
9.
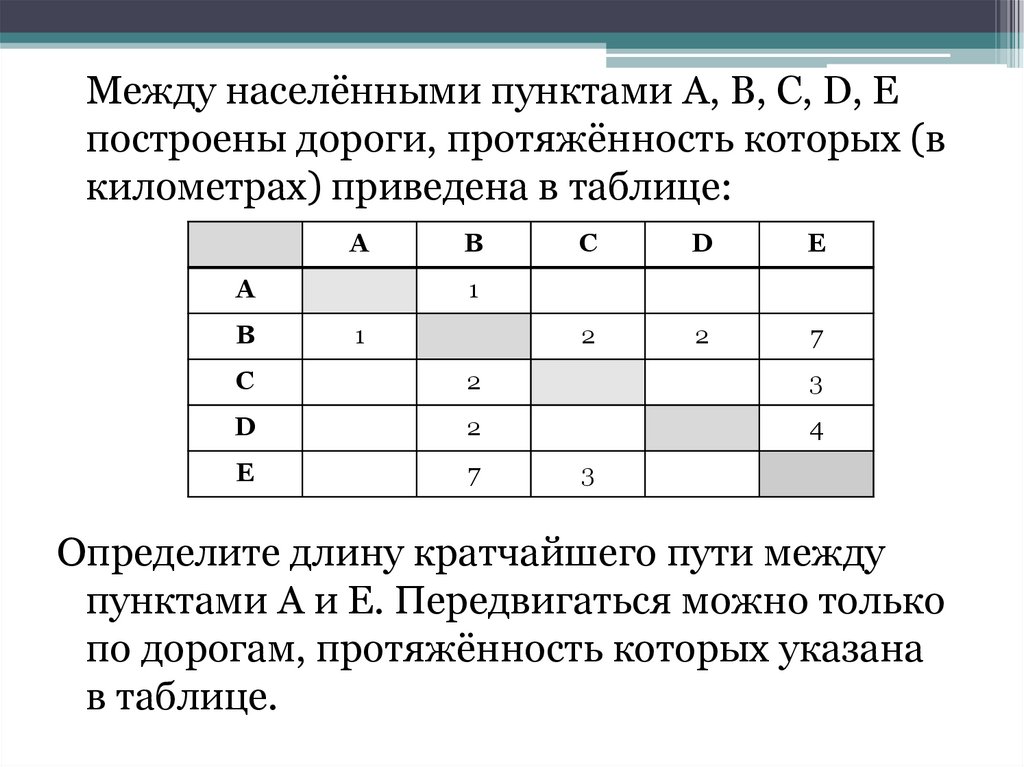
Между населёнными пунктами А, В, С, D, Епостроены дороги, протяжённость которых (в
километрах) приведена в таблице:
A
A
B
B
C
D
E
2
2
7
1
1
C
2
3
D
2
4
E
7
3
Определите длину кратчайшего пути между
пунктами А и E. Передвигаться можно только
по дорогам, протяжённость которых указана
в таблице.
10.
Решение. Найдём все варианты маршрутов из A в E ивыберем самый короткий.
Из пункта A можно попасть в пункт B.
Из пункта B можно попасть в пункты C, D, E.
Из пункта C можно попасть в пункт E.
Из пункта D можно попасть в пункт E.
A—B: длина маршрута 1 км.
A—B—C—E: длина маршрута 6 км.
A—B—D—E: длина маршрута 7 км.
A—B—E: длина маршрута 8 км.
Самый короткий путь: A—B—C—E. Длина маршрута 6
км.
Ответ: 6.
11.
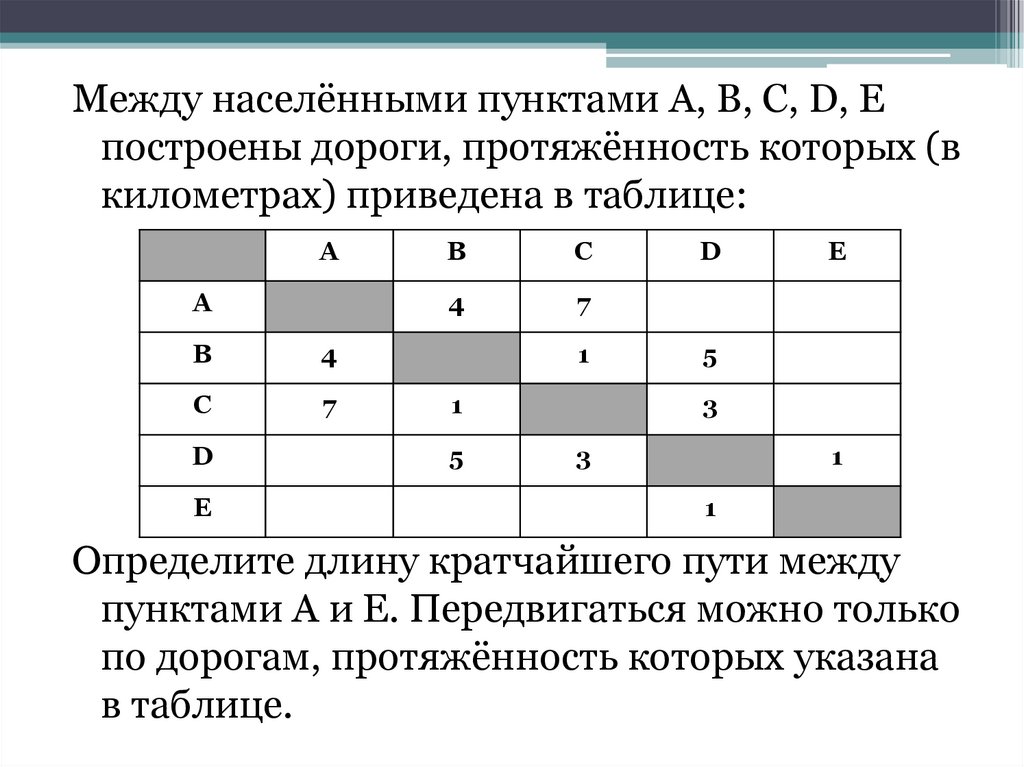
Между населёнными пунктами А, В, С, D, Епостроены дороги, протяжённость которых (в
километрах) приведена в таблице:
A
A
B
4
C
7
D
E
B
C
4
7
1
1
5
D
E
5
3
3
1
1
Определите длину кратчайшего пути между
пунктами А и E. Передвигаться можно только
по дорогам, протяжённость которых указана
в таблице.
12.
Решение. Найдём все варианты маршрутов из A в E ивыберем самый короткий.
Из пункта A можно попасть в пункты B, С.
Из пункта B можно попасть в пункты C, D.
Из пункта C можно попасть в пункт D.
Из пункта D можно попасть в пункт E.
A—B—C—D—E: длина маршрута 9 км.
A—B—D—E: длина маршрута 10 км.
A—C—D—E: длина маршрута 11 км.
Самый короткий путь: A—B—C—D—E. Длина
маршрута 9 км.
Ответ: 9.





 informatics
informatics








