Similar presentations:
Расчет показателей надежности нерезервированных невосстанавливаемых систем
1.
Расчет показателей надежности нерезервированныхневосстанавливаемых систем
2.
Критериями надежности невосстанавливаемых систем являются:1. Pc (t) – вероятность безотказной работы системы в течение времени t;
2. Тс – среднее время безотказной работы системы;
3. λ c(t) – интенсивность отказа системы в момент времени t;
4. fc (t) – плотность распределения времени до отказа.
Между этими показателями существуют следующие зависимости:
t
Pc t
=e
c t dt
a
Тt c= Pc t dt
0
f c t
c t
Pc t
f c t Qc t Pc t
t
Pc t 1 f c t dt
0
3.
Структурная схема нерезервированной системы, состоящей из nэлементов, приведена на рис. 1.
1
…
2
n
Рис. 1. Структурная схема нерезервированной системы
При отказе любою элемента наступает отказ системы. При этом
остальные элементы системы прекращают свою работу.
Показатели надежности такой системы вычисляются по формулам:
Pc t П Pj t
n
j 1
Ttc Pc t dt
0
n
c t j t
j 1
f c t f1 t P2 t ...Pn t P1 t f 2 t ...Pn t ... P1 t P2 t ... f n t
4.
где Pj (t) – вероятность безотказной работы j-го элемента. j=1, 2,...... n;fj (t) – плотность распределения времени до отказа j-гo элемента. j=1,
2,…n;
λj(t) – интенсивность отказа j-го элемента. j=1, 2,.....n.
Для случая постоянных интенсивностей отказов элементов имеют
место соотношения:
Pc t e ct
n
j j
j 1
Ttc
1
c
f c t c e t
c
5.
Пример 1. Нерезервированная система состоит из 5 элементов.Интенсивности их отказов приведены в табл. 1.
Таблица 1
Интенсивности отказов элементов
Номер элемента
λj , час-1
1
0,00007
2
0,00005
3
0,00004
4
0,00006
5
0,00004
Определим показатели надежности системы: интенсивность отказа,
среднее время безотказной работы, вероятность безотказной работы,
плотность распределения времени безотказной работы. Показатели
надежности P(t) и f(t) получить на интервале от 0 до 1000 часов с шагом 100
часов.
Решение. Вычислим интенсивность отказа и среднее время
безотказной работы системы:
n
c c 0,00007 0,00005 0,00004 0,00006 0,00004 0,00026 час 1
i 1
Ttc
1
c
1
3846 час
0,00026
6.
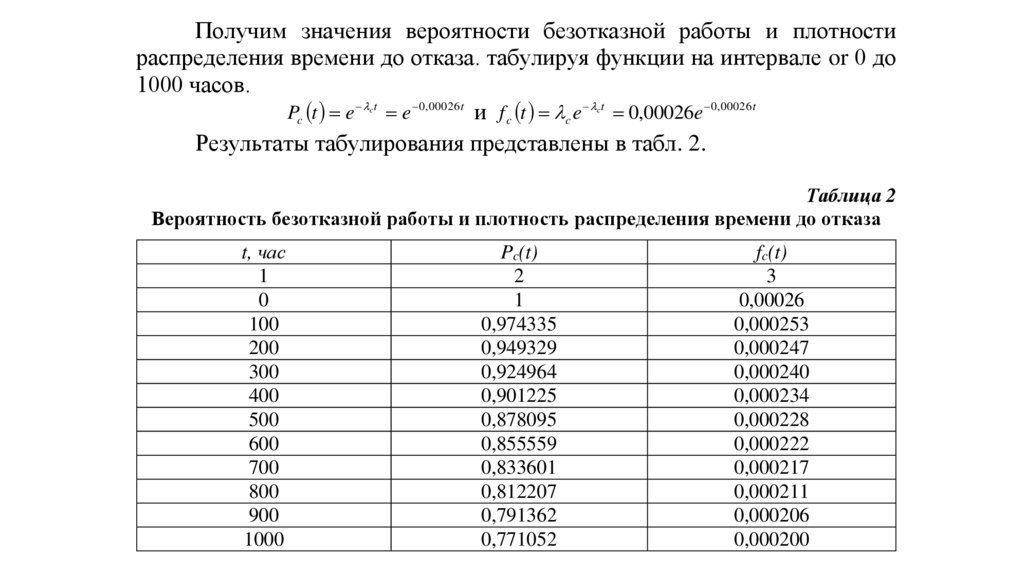
Получим значения вероятности безотказной работы и плотностираспределения времени до отказа. табулируя функции на интервале or 0 до
1000 часов.
Pc t e t e 0, 00026 t и f c t c e t 0,00026e 0, 00026 t
Результаты табулирования представлены в табл. 2.
c
c
Таблица 2
Вероятность безотказной работы и плотность распределения времени до отказа
t, час
1
0
100
200
300
400
500
600
700
800
900
1000
Pc(t)
2
1
0,974335
0,949329
0,924964
0,901225
0,878095
0,855559
0,833601
0,812207
0,791362
0,771052
fc(t)
3
0,00026
0,000253
0,000247
0,000240
0,000234
0,000228
0,000222
0,000217
0,000211
0,000206
0,000200
7.
Графическая иллюстрация Pc(t) и fc(t) показана на рис. 2 и 3.Рис. 2. Вероятность безотказной работы системы f(t)
8.
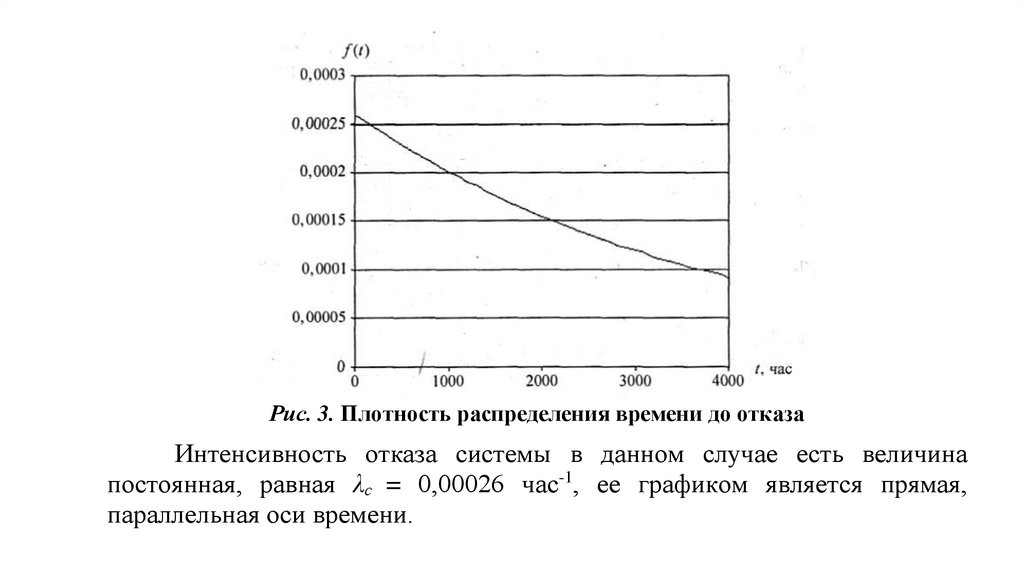
Рис. 3. Плотность распределения времени до отказаИнтенсивность отказа системы в данном случае есть величина
постоянная, равная λс = 0,00026 час-1, ее графиком является прямая,
параллельная оси времени.
9.
Пример 2. Нерезервированная система состоит из 5 элементов,имеющих различные законы распределения времени работы до отказа.
Виды законов распределения и их параметры приведены в табл. 3.
Таблица 3
Законы распределения времени до отказа
Номер
элемента
Закон
распределения
времени
до отказа
1
2
3
4
5
W(2; 1800)
Г(7; 300)
R(8·10-8)
Exp(0,002)
TN(2000; 90)
В табл. 3 и в дальнейшем приняты следующие обозначения законов
распределения:
W – Вейбулла;
Г – гамма;
R – Рэлея;
Ехр – экспоненциальный;
TN – усеченный нормальный;
N – нормальный;
U – равномерный.
В скобках указаны параметры распределений.
10.
Необходимо определить показатели надежности каждого элемента ивсей системы: вероятность безотказной работы; среднее время безотказной
работы; интенсивность отказа, плотность распределения времени
безотказной работы. Для показателей, зависящих от времени, получить
решение в виде таблиц и графиков.
Решение: в табл. 3 заданы параметры законов распределения времени
до отказа. Вычислим начальные моменты распределений: математические
ожидания и средние квадратические отклонения. Для этого воспользуемся
формулами связи моментов с параметрами распределений, которые
приведены в табл. 4.
В таблице введены следующие обозначения:
t
Ф0 t
x2
2
1
e dx – функция Лапласа;
2 0
Г ( ) х а 1е х dx – гамма-функция
0
11.
Таблица 4Связь параметров распределения с первыми двумя моментами
Распределение
1
Экспоненциальное Exp(λ)
Равномерное U(a, b), a≥0
Гамма Г(α, β)
σ
3
1
b a
m
2
1
a b
2
2 3
0 1 k
Усеченное нормальное
TN(m0, σ0)
m0 k 0
k
c
c
2
e
m0
0
m02
2 e02
1
0,5 Ф0
Вейбулла W(α, β)
4
Г 1 1
Нормальное N(m, σ) m>3σ
m
Рэлея R(λ)
k2
m0
0
4
4
Г 1 2 Г 2 1 1
12.
Определим математическое ожидание и среднее квадратичноеотклонение времени до отказа элементов.
Элемент 1. Распределение Вейбулла с параметром формы α=2 и
параметром масштаба β= 1800:
m 1800 Г (1,5) 1595 час, 1800 Г 2 Г 2 (1,5) 834 час
Элемент 2. Гамма распределение с параметром формы α=7 и
параметром масштаба β= 300:
m 7 300 2100час, 7 300 794 час.
Элемент 3. Pacпределение Рэлея с параметром λ=8·10-8:
m
4 8 10
3133час,
8
4
1638 час.
8
4 8 10
Элемент 4. Экспоненциальное распределение с параметром λ=0,0002:
m
1
5000час, m 5000 час.
0,0002
13.
Элемент 5. Усеченное нормальное распределение с параметрамиm0=2000, σ0=900:
k
1
m0
2 0,5 Ф0
0
e
m02
2 02
1
2000
2 0,5 Ф0
900
20002
е 900 0,0342
Значит,
m 2000 0,0342 900 2029 час,
2000
900 1 0,0342
0,0342 2 931 час.
900
Полученные значения сведены в табл. 5.
2
14.
Таблица 5Параметры законов распределения времени до отказа элементов
Номер элемента
Среднее время безотказной работы, час
Среднее квадратичное отклонение времени
безотказной работы, час
1
1595
2
2100
3
3133
4
5000
5
2029
834
794
1638
5000
931
Для вычисления вероятности безотказной работы и плотности
распределения времени до отказа элементов нам потребуются
аналитические выражения, которые приведены в табл. 6.
В гамма -распределении функции I , t
гамма-функция.
1
t
x 1e x dt есть неполная
Г 0
15.
Таблица 6Некоторые законы распределения вероятностей
Распределение
f(t)
P(t)
Экспоненциальное Exp(λ)
e t
c t
Равномерное U(a, b), a≥0
1
,a t b
b a
1, t<a;
b t
,a t b
b a
0, t>b
0, t<a, t>b
t 1
е
Г ( )
t
Гамма Г(α, β)
C
Усеченное нормальное
TN(m0, σ0)
m≥1,33σ
0 2
C
e
t
1 I ,
t m0 2
2 02
1
m0
t m0
C 0,5 Ф0
0
16.
Гамма Г(α, β)t
1
Г ( )
C
Усеченное нормальное
TN(m0, σ0)
m≥1,33σ
Рэлея R(λ)
Вейбулла W(α, β)
Нормальное N(m, σ) m>3σ
е
0 2
C
t
t m0 2
2 02
e
1
m0
0,5 Ф0
0
2 t e
1
e
1
e
r 2
t
t
2
t
1 I ,
Продолжение таблицы
6
t m0
C 0,5 Ф0
0
e
r 2
e
t m 2
2 2
t
t m
0,5 Ф0
17.
Равномерное и нормальное распределение имеют ограничения напараметры для того, чтобы их можно было использовать для решения задач
надежности в неотрицательной временной области (t≥0).
Вычислим вероятность безотказной работы элементов.
Элемент 1. Распределение Вейбулла:
P1 t e
t
e
t
1800
2
Элемент 2. Гамма-распределение:
t
x 1
t
P2 t
e dx 1 I , 1 I 7,
300
t Г ( )
x
Элемент 3. Распределение Рэлея:
P3 t e
t 2
e
8 10 8 t 2
18.
Элемент 4. Экспоненциальное распределение:P4 t e t e 0,0002t
Элемент 5. Усеченное нормальное распределение:
t m0
t 2000
0
,
5
Ф
0,5 Ф0
0
x m0
2
c
0
900
2 0
P5 t
e
dx
m0
2000
0 2 t
0,5 Ф0
0,5 Ф0
900
0
2
Табулируя эти функции от 0 до 2000 часов с шагом 100 часов, получим
табл. 7.
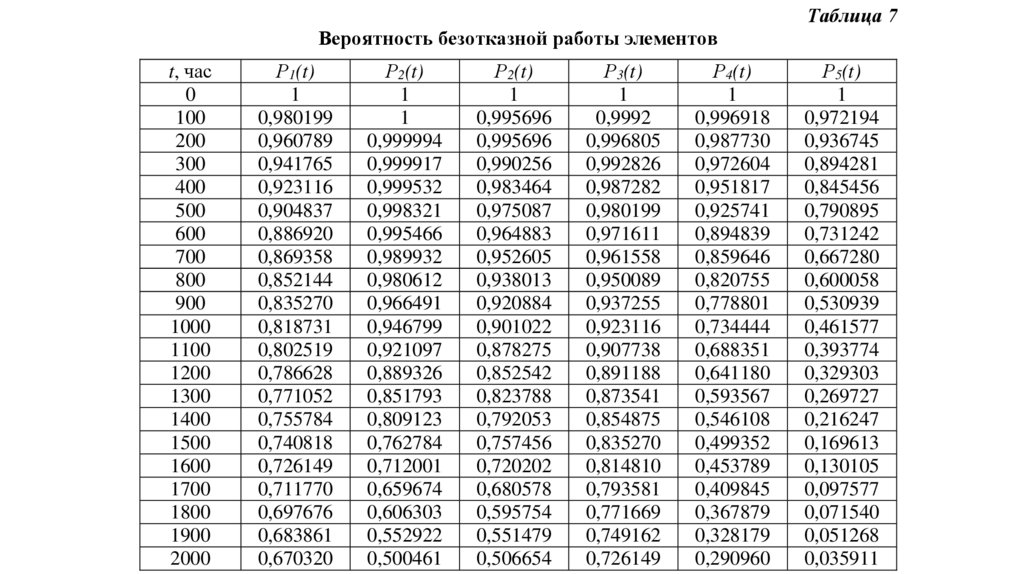
В последнюю колонку записаны значения вероятностей безотказной
работы системы, которые определяются произведением вероятностей
безотказной работы элементов;
Pc t P1 t P2 t P3 t P4 t P5 t
19.
Таблица 7Вероятность безотказной работы элементов
t, час
0
100
200
300
400
500
600
700
800
900
1000
1100
1200
1300
1400
1500
1600
1700
1800
1900
2000
Р1(t)
1
0,980199
0,960789
0,941765
0,923116
0,904837
0,886920
0,869358
0,852144
0,835270
0,818731
0,802519
0,786628
0,771052
0,755784
0,740818
0,726149
0,711770
0,697676
0,683861
0,670320
Р2(t)
1
1
0,999994
0,999917
0,999532
0,998321
0,995466
0,989932
0,980612
0,966491
0,946799
0,921097
0,889326
0,851793
0,809123
0,762784
0,712001
0,659674
0,606303
0,552922
0,500461
Р2(t)
1
0,995696
0,995696
0,990256
0,983464
0,975087
0,964883
0,952605
0,938013
0,920884
0,901022
0,878275
0,852542
0,823788
0,792053
0,757456
0,720202
0,680578
0,595754
0,551479
0,506654
Р3(t)
1
0,9992
0,996805
0,992826
0,987282
0,980199
0,971611
0,961558
0,950089
0,937255
0,923116
0,907738
0,891188
0,873541
0,854875
0,835270
0,814810
0,793581
0,771669
0,749162
0,726149
Р4(t)
1
0,996918
0,987730
0,972604
0,951817
0,925741
0,894839
0,859646
0,820755
0,778801
0,734444
0,688351
0,641180
0,593567
0,546108
0,499352
0,453789
0,409845
0,367879
0,328179
0,290960
Р5(t)
1
0,972194
0,936745
0,894281
0,845456
0,790895
0,731242
0,667280
0,600058
0,530939
0,461577
0,393774
0,329303
0,269727
0,216247
0,169613
0,130105
0,097577
0,071540
0,051268
0,035911
20.
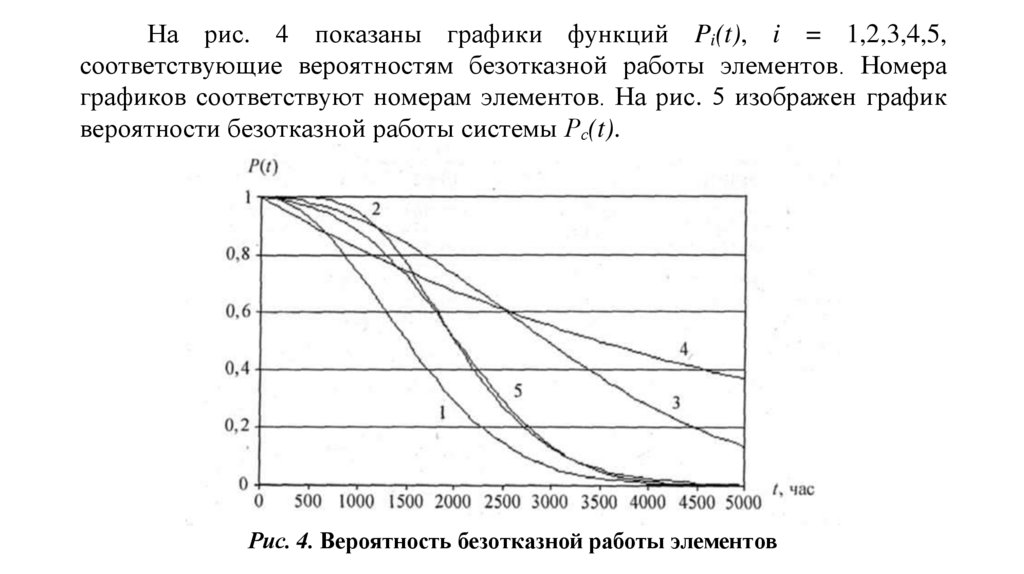
На рис. 4 показаны графики функций Pi(t), i = 1,2,3,4,5,соответствующие вероятностям безотказной работы элементов. Номера
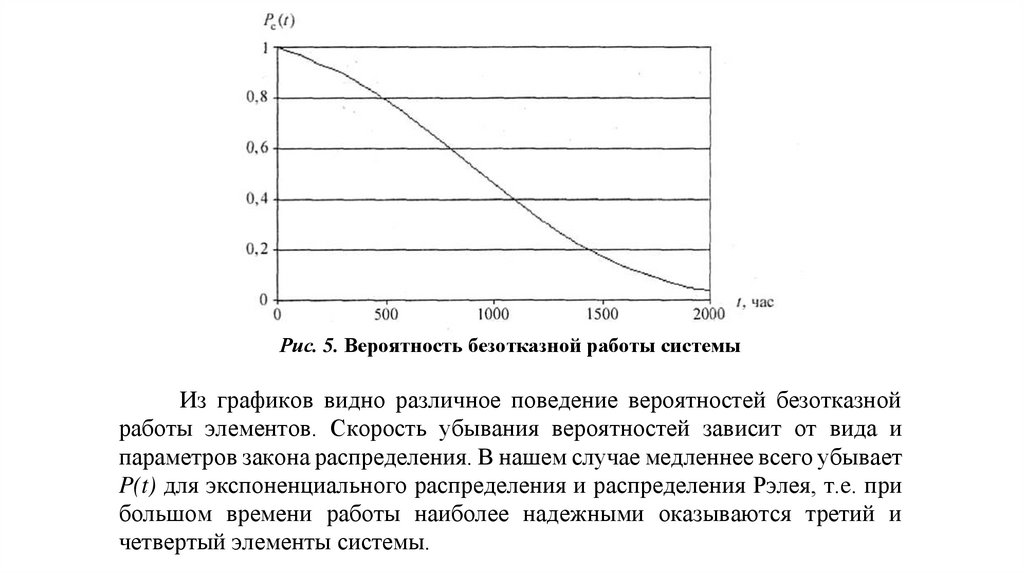
графиков соответствуют номерам элементов. На рис. 5 изображен график
вероятности безотказной работы системы Рс(t).
Рис. 4. Вероятность безотказной работы элементов
21.
Рис. 5. Вероятность безотказной работы системыИз графиков видно различное поведение вероятностей безотказной
работы элементов. Скорость убывания вероятностей зависит от вида и
параметров закона распределения. В нашем случае медленнее всего убывает
P(t) для экспоненциального распределения и распределения Рэлея, т.e. при
большом времени работы наиболее надежными оказываются третий и
четвертый элементы системы.
22.
Вычислим среднее время безотказной работы системы:0
0
T1 Pc t dt P1 (t ) P2 (t ) P3 (t ) P4 (t ) P5 (t )dt
По формуле Симпсона:
h n 1
k
T1 1 3 1 P1 (kh) P2 (kh) P3 (kh) P4 (kh) P5 (kh) ,
3 k 1
где n – число точек;
h – шаг интегрирования, выбираемый из условия обеспечения требуемой
точности.
Расчеты показывают, что для данных табл. 7 T1=976,3 час.
23.
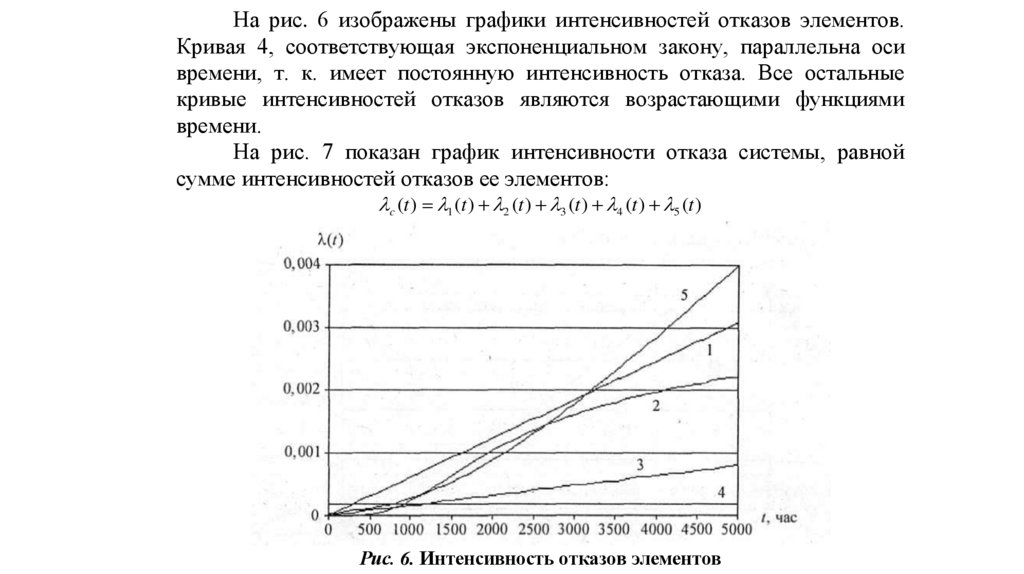
На рис. 6 изображены графики интенсивностей отказов элементов.Кривая 4, соответствующая экспоненциальном закону, параллельна оси
времени, т. к. имеет постоянную интенсивность отказа. Все остальные
кривые интенсивностей отказов являются возрастающими функциями
времени.
На рис. 7 показан график интенсивности отказа системы, равной
сумме интенсивностей отказов ее элементов:
c (t ) 1 (t ) 2 (t ) 3 (t ) 4 (t ) 5 (t )
Рис. 6. Интенсивность отказов элементов
24.
Рис. 7. Интенсивность отказа системыИнтенсивность отказа системы также является возрастающей
функцией времени, что говорит о том, что система является стареющей, а
закон распределения времени до ее отказа не экспоненциальный.
25.
Вычислим плотности распределениябезотказной работы элементов.
Элемент 1. Распределение Вейбулла:
1
t
f1 (t ) e
t
2t
e
2
1800
вероятностей
1
1800
2
Элемент 2. Гамма-распределение:
1
t
t
6
t
300
f 2 (t )
e
e
à ( )
300 7 Ã (7)
t
Элемент 3. Распределение Рэлея:
f 3 (t ) 2 te
t 2
8
2 8 10 te
8 10 8 t
2
времени
26.
Элемент 4. Экспоненциальное распределение:f 4 (t ) e t 0,0002e 0,0002t
Элемента 5. Усеченное нормальное распределение:
f 5 (t )
c
0 2
e
t m0 2
2 02
1
2000
900 2 0,5 Ô 0
900
å 2000 2
å
2 9002
Табулируя плотности распределения от 0 до 2000 часов с шагом 100
часов, получим табл. 8.
27.
Таблица 8Плотность распределения времени безотказной работы элементов
t, час
F1(t)
f2(t)
f3(t)
f4(t)
F5(t)
0
100
200
300
400
500
600
700
800
900
1000
1100
1200
1300
1400
1500
0,0002
0,000196
0,000192
0,000188
0,000185
0,000181
0,000177
0,000174
0,000170
0,000167
0,000164
0,000161
0,000157
0,000154
0,000151
0,000148
0
0
0
0,000002
0,000007
0,000019
0,00004
0,000072
0,000116
0,000168
0,000227
0,000288
0,000347
0,000402
0,000450
0,000487
0,000038
0,000048
0,000061
0,000075
0,000092
0,000112
0,000134
0,000158
0,000185
0,000213
0,000242
0,000272
0,000303
0,000332
0,000360
0,000385
0
0,000016
0,000032
0,000048
0,000063
0,000078
0,000093
0,000108
0,000122
0,000135
0,000148
0,000160
0,000171
0,000182
0,000191
0,000200
0
0,000062
0,000122
0,000180
0,000235
0,000286
0,000331
0,000371
0,000405
0,000433
0,000453
0,000467
0,000475
0,000476
0,000472
0,000462
28.
600700
800
900
1000
1100
1200
1300
1400
1500
1600
1700
1800
1900
2000
0,000177
0,000174
0,000170
0,000167
0,000164
0,000161
0,000157
0,000154
0,000151
0,000148
0,000145
0,000142
0,000140
0,000137
0,000134
0,00004
0,000072
0,000116
0,000168
0,000227
0,000288
0,000347
0,000402
0,000450
0,000487
0,000514
0,000530
0,000535
0,000531
0,000517
0,000134
0,000093
0,000331
0,000158
0,000108
0,000371
0,000185
0,000122
0,000405
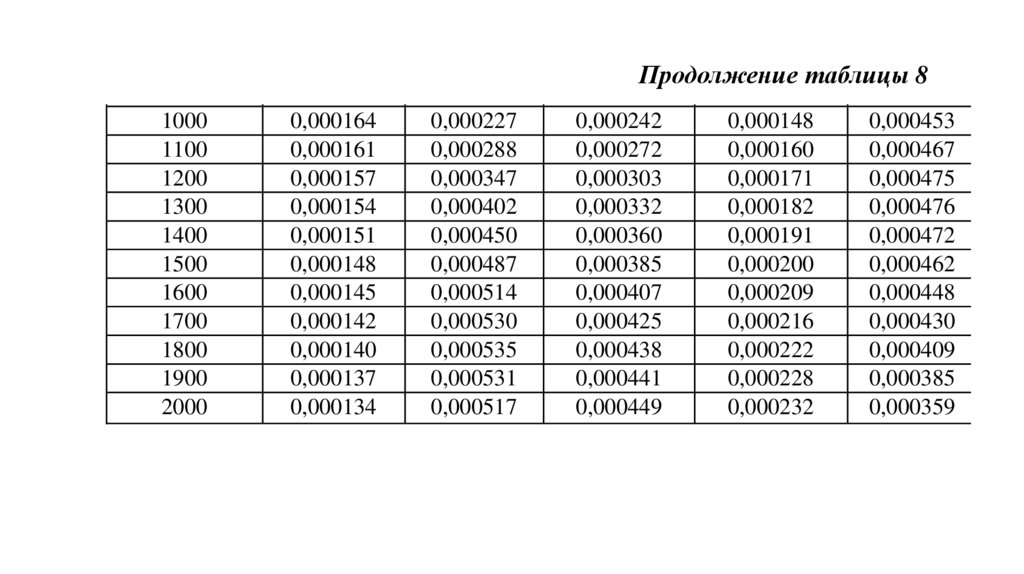
Продолжение
таблицы
8
0,000213
0,000135
0,000433
0,000242
0,000148
0,000453
0,000272
0,000160
0,000467
0,000303
0,000171
0,000475
0,000332
0,000182
0,000476
0,000360
0,000191
0,000472
0,000385
0,000200
0,000462
0,000407
0,000209
0,000448
0,000425
0,000216
0,000430
0,000438
0,000222
0,000409
0,000441
0,000228
0,000385
0,000449
0,000232
0,000359
29.
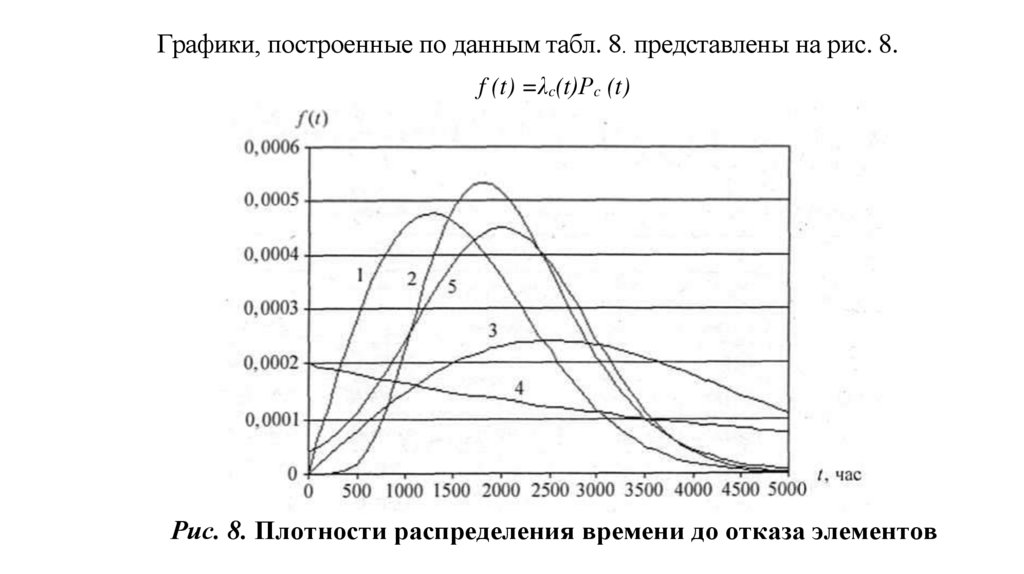
Графики, построенные по данным табл. 8. представлены на рис. 8.f (t) =λc(t)Рc (t)
Рис. 8. Плотности распределения времени до отказа элементов
30.
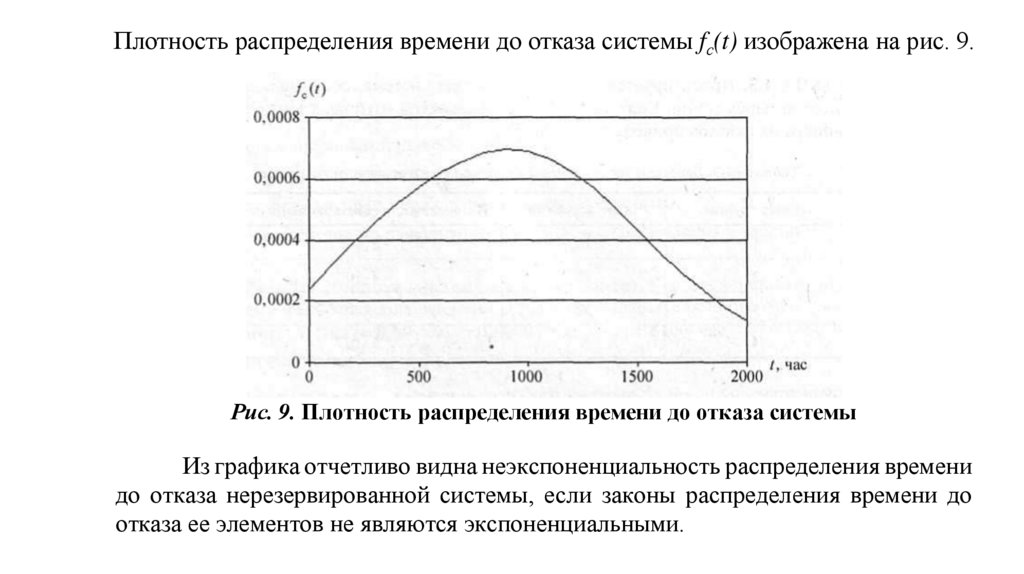
Плотность распределения времени до отказа системы fс(t) изображена на рис. 9.Рис. 9. Плотность распределения времени до отказа системы
Из графика отчетливо видна неэкспоненциальность распределения времени
до отказа нерезервированной системы, если законы распределения времени до
отказа ее элементов не являются экспоненциальными.
31.
Задание на практическую работу №5:Выполнить расчеты показателей надежности
невосстанавливаемых систем по заданиям
нерезервированных






















 industry
industry








