Численные методы решения систем нелинейных уравнений. Метод простых итераций (лекция № 4)

1.

Численные методы решения систем нелинейных
уравнений. Метод простых итераций.
Рассмотрим систему нелинейных уравнений :
f1 ( x1 , x2 ,..., xn ) 0
f ( x , x ,..., x ) 0
2 1 2
n
f n ( x1 , x2 ,..., xn ) 0

2.

Система нелинейных уравнений в операторной
форме:
F(X ) 0
f1
f2
Вектор функция : F
...
f
n
x1
x2
Вектор неизвестных : X
...
x
n

3.

Математическое моделирование приводит к
решению мат. моделей в виде систем
нелинейных уравнений. Не всегда удаётся
найти решение аналитически, поэтому
используются численные методы.
Численное решение систем нелинейных
уравнений состоит из 2-х этапов:
1. Отделение корней
2. Уточнение корней

4.

1. Отделение корней.
Рассмотрим систему нелинейных уравнений из двух
уравнений и двух неизвестных:
n 2
f1 ( x1 , x2 ) 0
f 2 ( x1 , x2 ) 0

5.

Необходимо построить кривые f1(x1,x2)=0 и
f2(x1,x2)=0 в системе координат (x1,x2).

6.

Точки пересечения кривых являются
решением системы.
D1,D2 – области существования решения.
В частности: D1:{a1<x1<a2, b1<x2<b2}.
Примечание: Для систем нелинейных
уравнений с числом неизвестных n≥3 нет
общих методов определения областей
существования решения системы.

7.

2. Уточнение корней.
Методы уточнения корней систем нелинейных
уравнений получены путем обобщения
методов для нахождения корней нелинейных
уравнений с одним неизвестным.
2.1.Метод простой итерации
Рассмотрим систему нелинейных уравнений:
f1 ( x1 , x2 ,..., xn ) 0
f ( x , x ,..., x ) 0
n
n 1 2
(4)

8.

2.1.1. Систему (4) путем элементарных тождественных
преобразований приводим к виду:
x1 1 ( x1 , x2 ,..., xn )
x ( x , x ,..., x )
2
2
1
2
n
...
xn n ( x1 , x2 ,..., xn )
(5)
Полученные формулы называются итерационными и
используются для пересчета последующих значений
приближенного решения.

9.

2.1.2. Из области существования решения
произвольно выбирается начальное
приближение. Начальное приближение
подставляем в правую часть итерационных
формул (5). Вычисляем и получаем новое
приближенное решение.

10.

2.1.3. Для обеспечения сходимости необходимо,
чтобы в области существования корня D
выполнялось условие:
Ф( x1 ,..., x n ) 1, где
1
xn
матрица частных производных
n
xn
1
x1
Ф( x1 ,..., x n )
n
x1
n
Ф( x1 ,..., x n ) max aij норма матрицы
j 1
i 1,..., n

11.

2.1.4. Для завершения итерационного процесса
используется следующий критерий останова:
, заданная точность
max | x
i 1,..., n
k 0 ,1, 2 ,...
(k )
i
( k 1)
i
x
|

12.

Пример. Уточнить корни методом простой итерации:
x12 x22 1
ln x1 2 x2 1
Области существования корней :
D1 : {0,8 x1 1, 0,5 x2 0,3}
D2 : {0 x1 0,2, 0,8 x2 1}
Область определения системы :
x1 0
x2 любое

13.

Приводим систему к виду (5).
x 1 x2
2
1
1
x2 (1 ln x1 )
2
Итерационные формулы :
x ( x , x ) 1 x2
1 1
2
2
1
1
x2 2 ( x1 , x2 ) (1 ln x1 )
2
(6)

14.

Проверяем условие сходимости для D1:
1
1
x2
0,
x1
x2
1 x22
2
1 2
,
0
x1
2 x1 x2
Матрица частных производных :
0
Ф( x1 , x2 )
1
2x
1
2
1 x2
0
x2

15.

Найдём норму матрицы Ф( x1 , x2 ) в области
D1 : {0,8 x1 1, 0,5 x2 0,3}
x2
1
Ф( x1 , x2 ) max(( 0
); (
0))
2 x1
1 x22
Рассмотрим пары граничных точек из D1 :
1) x1 0,8, x2 0,5
0,5
1
Ф( x1 , x2 ) max(( 0
); (
0))
2 0,8
1 ( 0,5) 2
max( 0,577;0,625) 1
Условие сходимости выполнено.

16.

2) x1 1, x2 0,3
( 0,3)
1
Ф( x1 , x2 ) max(( 0
); (
0))
2 1
1 ( 0,3) 2
max( 0,314;0,5) 1
Условие сходимости выполнено.

17.

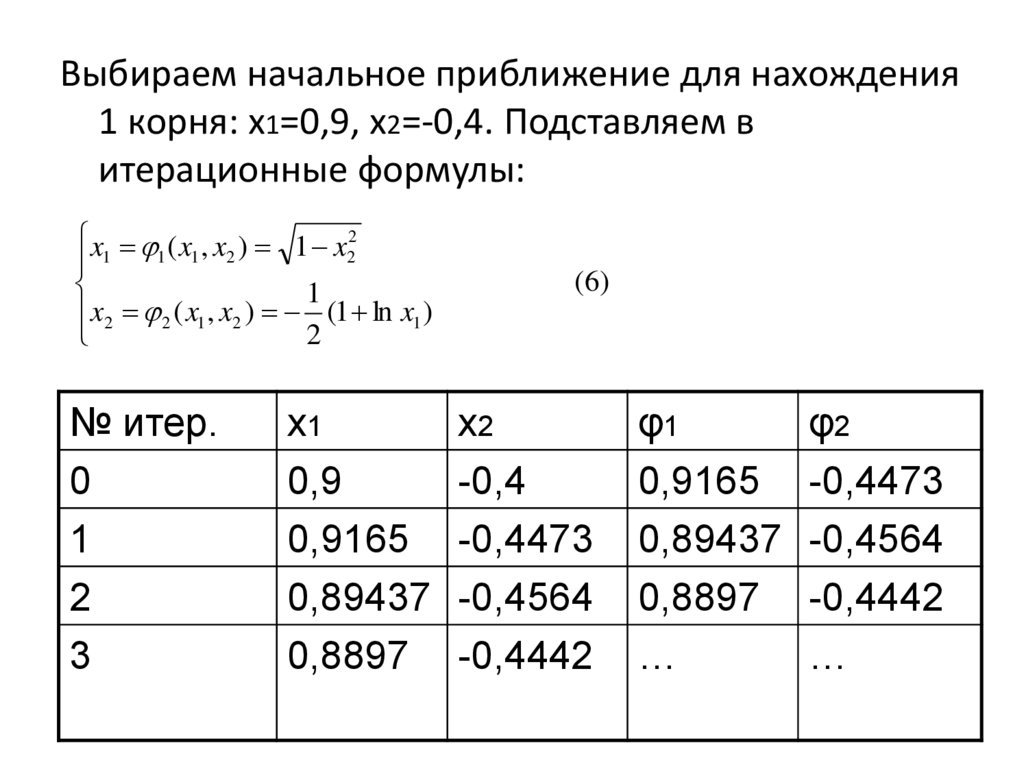
Выбираем начальное приближение для нахождения
1 корня: x1=0,9, x2=-0,4. Подставляем в
итерационные формулы:
x ( x , x ) 1 x2
1 1
2
2
1
1
x
(
x
,
x
)
(1 ln x1 )
2
2
1
2
2
№ итер.
0
1
2
3
(6)
х1
х2
0,9
-0,4
0,9165 -0,4473
0,89437 -0,4564
0,8897 -0,4442
φ1
φ2
0,9165 -0,4473
0,89437 -0,4564
0,8897 -0,4442
…
…

18.

Проверяем условие сходимости для D2:
1
1
x2
0,
x1
x2
1 x22
2
1 2
,
0
x1
2 x1 x2
Матрица частных производных :
0
Ф( x1 , x2 )
1
2x
1
2
1 x2
0
x2

19.

Найдём норму матрицы Ф( x1 , x2 ) в области
D2 : {0 x1 0,2; 0,8 x2 1}
x2
1
Ф( x1 , x2 ) max(( 0
); (
0))
2 x1
1 x22
Рассмотрим пару граничных точек из D2 :
1) x1 0, x2 0,8
0,8
1
Ф( x1 , x2 ) max(( 0
); (
0))
2 0
1 ( 0,8) 2
max( 1,333; ) 1
Условие сходимости не выполнено.

20.

Так как условие сходимости не выполненно,
x 1 x2
2
1
то формулы
1
x2 (1 ln x1 )
2
не подходят для итерационного процесса
преобразуем исходную систему и получим
новые итерационные формулы :
x1 1 ( x1 ; x2 ) e (1 2 x2 )
2
x
(
x
;
x
)
1
x
2
2
1
2
1

21.

Проверяем условие сходимости для D2 ,используя
новые итерационные формулы:
1
1
(1 2 x2 )
0,
2e
x1
x2
2
x1
2
,
0
x1
1 x12 x2
Матрица частных производных :
(1 2 x2 )
0
2e
x1
Ф( x1 , x2 )
0
2
1 x1

22.

Найдём норму матрицы Ф( x1 , x2 ) в области
D2 : {0 x1 0,2; 0,8 x2 1}
Ф( x1 , x2 ) max(( 0 2e
(1 2 x2 )
); (
x1
1 x
2
1
0))
Рассмотрим пару граничных точек из D2 :
1) x1 0, x2 0,8
Ф( x1 , x2 ) max(( 0 2e
(1 2 0.8 )
0
); (
0))
1 0
max( 0.14855;0) 1
Условие сходимости выполнено.

23.

2) x1 0,2; x2 1
Ф( x1 , x2 ) max(( 0 2e
(1 2 1)
0
); (
0))
1 0,2
max( 0,099;0) 1
Условие сходимости выполнено.

24.

Выбираем начальное приближение для нахождения
2 корня: x1=0,1, x2=0,9. Подставляем в
итерационные формулы:
(1 2 x2 )
x
(
x
;
x
)
e
1 1
2
1
2
x
(
x
;
x
)
1
x
2
1
2
1
2
№ итер.
х1
х2
φ1
φ2
0
0,1
0,8
0,074273578 0,994987
1
0,074274 0,994987 0,0502887 0,997238
2
0,050289 0,997238 0,050062863 0,998735
3
0,050063 0,998735
…….
…….