Математические особенности движения тела брошенного под углом к горизонту

1.

1
Муниципальное бюджетное образовательное учреждение
«Лицей №40»
Нижегородский район г.Н.Новгород
Математические особенности движения тела брошенного
под углом к горизонту
2023
Выполнил: Филиппов Максим Михайлович 10АТ
Научный руководитель: Андрей Александрович Смирнов

2.

2
ИДЕЯ, ЗАДАЧИ, ПЛАН.
Идея: математика - основной язык в физике, многие прикладные задачи тесно связывают физическую и математическую
составляющие. Например, кинематика очень математична, при этом многие задачи одновременно интересна с точки
зрения обеих наук. Особо ярко это проявляется в разделе баллистики в школе представленном темой тело, брошенное под
углом к горизонту.
Задача работы: выяснить какой из способов нахождения пути тела брошенного под углом к горизонту наиболее точный,
рациональный, прибегнув к связи физики с математикой с помощью аппроксимации функций и базовых
тригонометрических формул.
План работы:
1. Нахождение пути через сложение двух прямолинейных движений.
2. Вывод уравнения траектории, вывод всех остальных параметров.
3. Траектория – парабола, вывод радиуса кривизны.
4. Что такое аппроксимация функции?
5. Аппроксимация параболы окружностями через радиус кривизны в данной точке.
6. Аппроксимация параболы 2-мя трапециями.
7. Выводы.
8. Дальнейшие планы развития работы.

3.

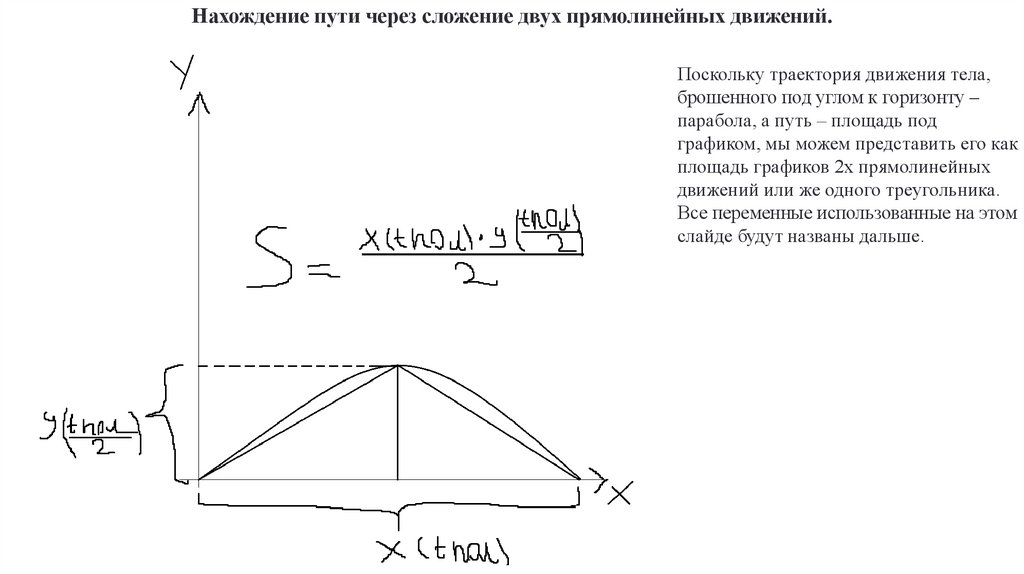
Нахождение пути через сложение двух прямолинейных движений.
Поскольку траектория движения тела,
брошенного под углом к горизонту –
парабола, а путь – площадь под
графиком, мы можем представить его как
площадь графиков 2х прямолинейных
движений или же одного треугольника.
Все переменные использованные на этом
слайде будут названы дальше.

4.

Вывод уравнения траектории, вывод всех остальных параметров.
h max
L

5.

Вывод уравнения траектории, вывод всех остальных параметров.
h max
L

6.

Траектория – парабола, вывод радиуса кривизны.

7.

Что такое аппроксимация функции?
Аппроксимацией функции называется приближенное представление сложной (имеющей громоздкое математическое
представление) или заданной в виде таблицы функции f (x) более простой функцией y(х), имеющей минимальные
отклонения от исходной функции в заданной. области х. По сути, аппроксимация – это моделирование
сложной функции более простой с вычислительной точки зрения функцией.

8.

Аппроксимация параболы окружностями через радиус кривизны в данной точке.

9.

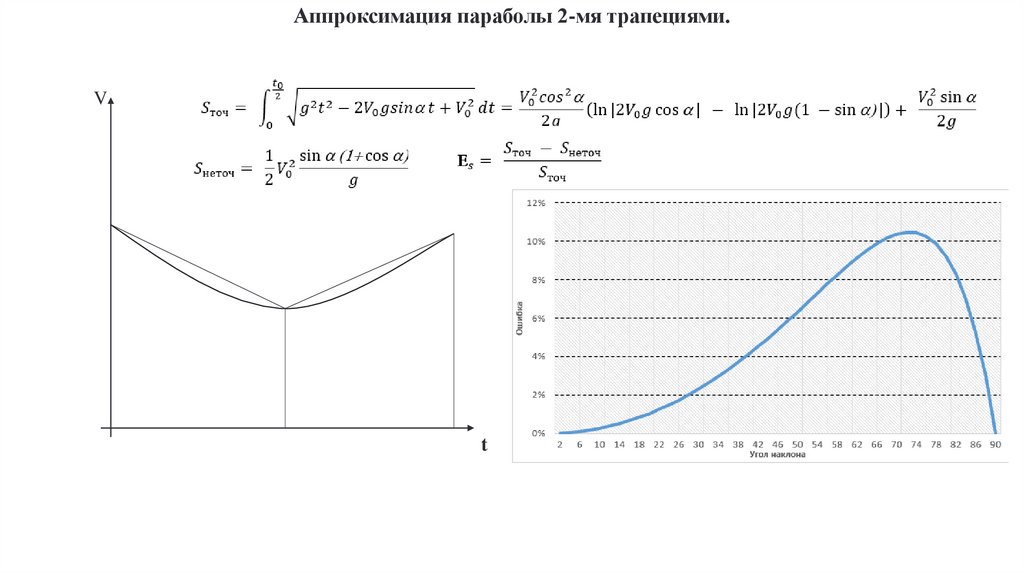
Аппроксимация параболы 2-мя трапециями.
V
t

10.

Выводы.
Из приведённых выше опытов, не сложно сделать вывод, что никакой способ расчёта длины пути не
сравнится с честным интегрированием по точности. В то же время, при аппроксимации графика V(t) двумя
трапециями результат вычислений получается более чем удовлетворительный, погрешность вычислений
находится в пределах 11%, а для большинства возможных углов наклона даже меньше 5%. Я считаю что эта
работа была для меня очень полезна, т.к. я познакомился с понятием аппроксимации, проинтегрировал
площадь под графиком параболы и в целом изучил одну из моих любимых тем кинематики поближе.

11.

Дальнейшие планы развития работы.
Но останавливаться на достигнутом мы не планируем, и в наши дальнейшие планы входят:
• Реализация идеи расчета подобных интегралов численными методами, методом палетки;
• При помощи численных методов с использованием ПК планируется исследование модели с учётом вязкого
трения о воздушные массы
• Планируется завершение аппроксимации графика параболы через графики окружностей с различными
радиусами кривизны

12.

Спасибо за внимание