Similar presentations:
Нахождение пределов. Первый замечательный предел
1.
№89Нахождение пределов.
Первый замечательный
предел
2.
Повторим:1. Какая функция называется непрерывной в
точке?
2. Какая функция называется непрерывной на
отрезке?
3. Если функции и непрерывны в точке а, то что
можно сказать о их сумме, произведении и о
частном?
4. Что вы можете сказать о
непрерывнострациональной функции?
5 . Что вы можете сказать о непрерывности
дробно – рациональной функции?
6. Какими свойствами обладают непрерывные
функции?
3.
.Правило 1.
lim f x g x lim f x lim g x
x a
x a
x a
Правило 2.
lim f x g x lim f x lim g x
Правило 3.
lim f x
f x
lim
x a
x a g x
lim g x
.
.
x a
x a
x a
x a
4.
sin xlim
1
x 0
x
5.
https://youtu.be/DqRWgnw4l6c6.
Переходим в полученном неравенстве к пределупри x 0
sin x
lim
cos
x
lim
lim
1
x 0
x 0
x 0
x
1
Следовательно, по
признаку
предела:
sin x
lim
1
x 0
x
1
существования
7.
Следствия из первого замечательного предела1°
2°
3°
4°
8.
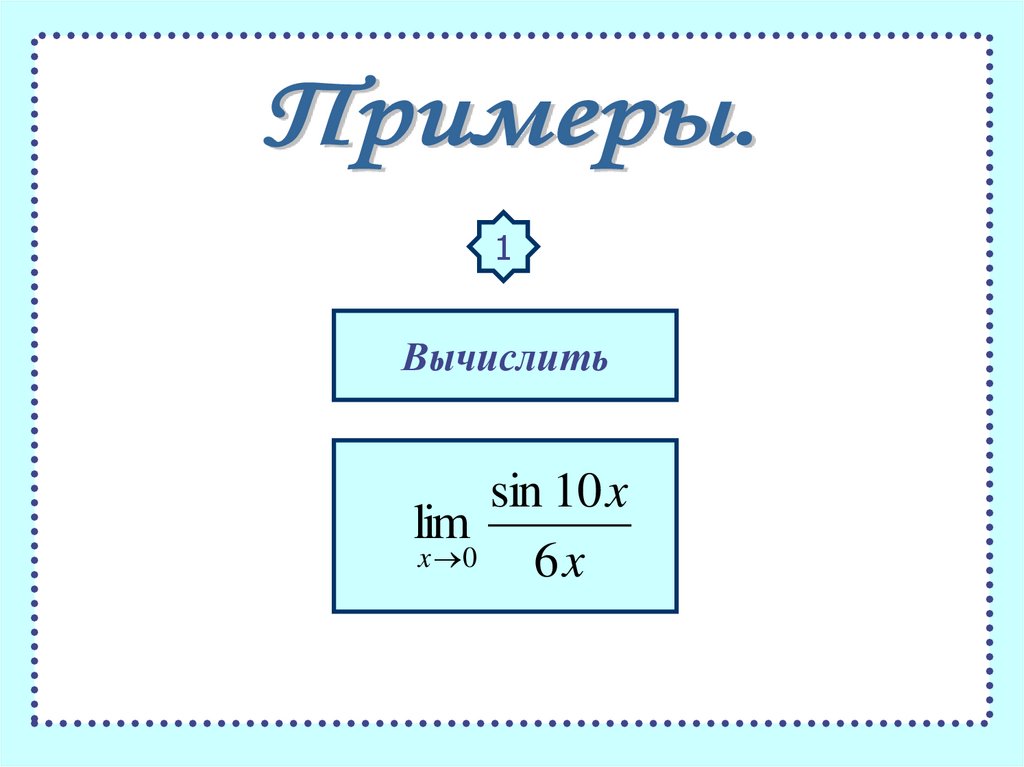
1Вычислить
sin 10 x
lim
x 0
6x
9.
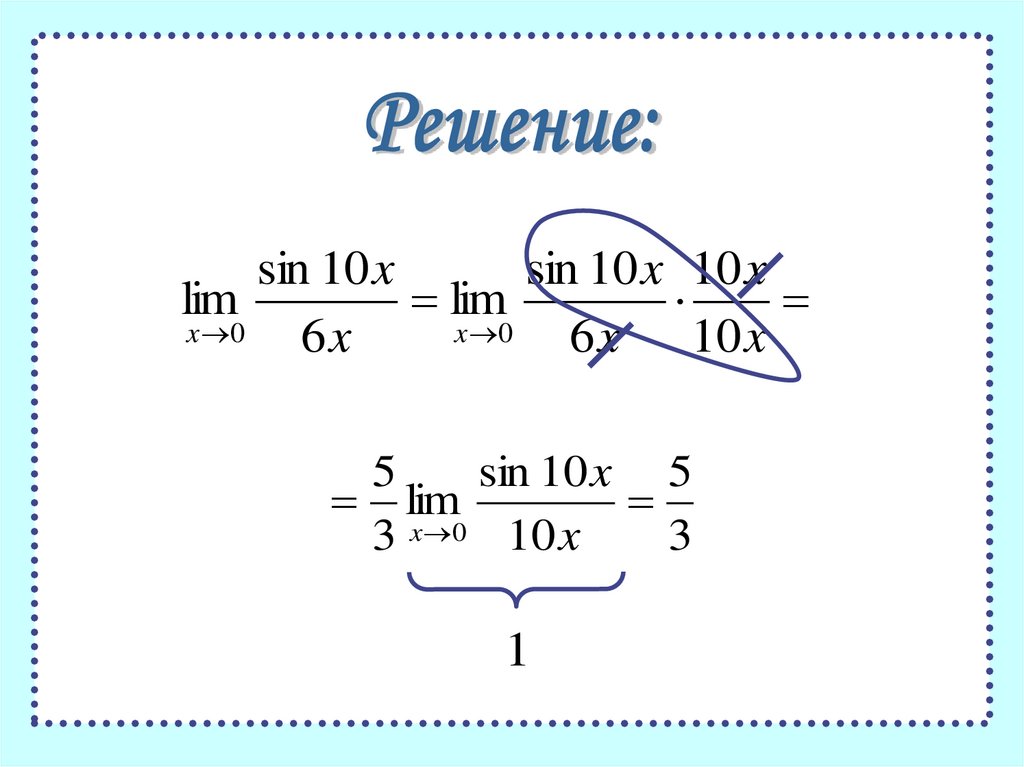
sin 10 xsin 10 x 10 x
lim
lim
x 0
x 0
6x
6 x 10 x
5
sin 10 x 5
lim
3 x 0 10 x
3
1
10.
Вычислите пределы1.
2.
3.
sin 5 x / 2
lim
x 0
x
sin 4 x
x 0 6 x
lim
sin 8 x
x 0 sin 12 x
lim
4.
5.
6.
4x
lim
x 0 sin 2 x
3x 2
lim 2
x 0 sin 3 x / 2
sin 2 3x
lim
x 0
3x








 mathematics
mathematics








