Рациональные уравнения как математические модели реальных ситуаций

1.

РАЦИОНАЛЬНЫЕ
УРАВНЕНИЯ КАК
МАТЕМАТИЧЕСКИЕ
МОДЕЛИ
РЕАЛЬНЫХ СИТУАЦИЙ

2.

Пример 1: Перегон в 60 км поезд должен был проехать с
постоянной скоростью за определенное расписанием
время. Простояв у семафора перед перегоном 5 мин,
машинист вынужден был увеличить скорость
прохождения перегона на 10км/ч, чтобы наверстать к
окончанию прохождения перегона потерянные 5 мин. с
какой скоростью поезд должен был пройти перегон по
расписанию?
Первый этап. Составление математической модели
60 км - путь
s=vt
х км/ч – скорость поезда по расписанию
60
ч – время, отведенное расписанием на прохождение перегона
x
(х+10) км/ч – скорость поезда по расписанию
60
ч – время, затраченное на прохождение перегона
x 10
60
60
1
на 5 мин
ч
x x 10
12
60
60
1
.
x x 10 12

3.

Второй этап. Работа с составленной моделью.
60
60
1
0.
x x 10 12
12(х+10) 12х
х(х+10)
60
60
1
720( x 10) 720 x x( x 10)
x
x 10 12
12 x( x 10)
x 2 10 x 7200
.
12 x( x 10)
x 2 10 x 7200 0;
x 2 10 x 7200 0;
10 10 2 4 1 ( 7200) 10 28900 10 170
x1, 2
;
2
2
2
10 170
10 170
x2
90.
x1
80;
2
2
12 x( x 10) 0
Третий этап. Ответ на вопрос задачи.
x 80
x 90
80 км / ч

4.

Пример 2: Пристани А и В расположены на реке, причем
В – на 80 км ниже по течению, чем А. Катер прошел
путь из А в В и обратно за 8ч 20 мин. За какое время
катер прошел расстояние от А до В и расстояние от
В до А, если известно, что его собственная скорость
(скорость в стоячей воде) равна 20 км/ч?
Первый этап. Составление математической модели
х км/ч – скорость течения реки;
(20+х) км/ч – скорость движения катера по течению;
(20-х) км/ч – скорость движения катера против течения;
80
ч – время движения катера по течению;
20 x
80
ч – время движения катера против течения.
20 x
80
80
25
1 25
.
8 ч 20 мин 8 ч
20 x 20 x 3
3 3

5.

Второй этап. Работа с составленной моделью.
80
80
25
.
20 x 20 x 3
1 25
1
80
;
20 x 20 x 3
1 5
1
16
;
20 x 20 x 3
16
(20 x) (20 x) 5
;
(20 x)(20 x)
3
1920 5(400 x 2 )
0;
3(20 x)(20 x)
5 x 2 80
0;
3(20 x)(20 x)
5 x 2 80 0;
x1,2 4.
640
5
0;
(20 x)(20 x) 3
x 2 16;
640 3 5(20 x)(20 x)
0;
3(20 x)(20 x)
3(20 x)(20 x) 0.
ОДЗ:

6.

Третий этап. Ответ на вопрос задачи.
x 4
x 4
80
ч
20 x
80
24
10
1
3
3
3
1
3 3 ч 20 мин
3
80
ч
20 x
80
5ч
16
3 ч 20 мин; 5 ч

7.

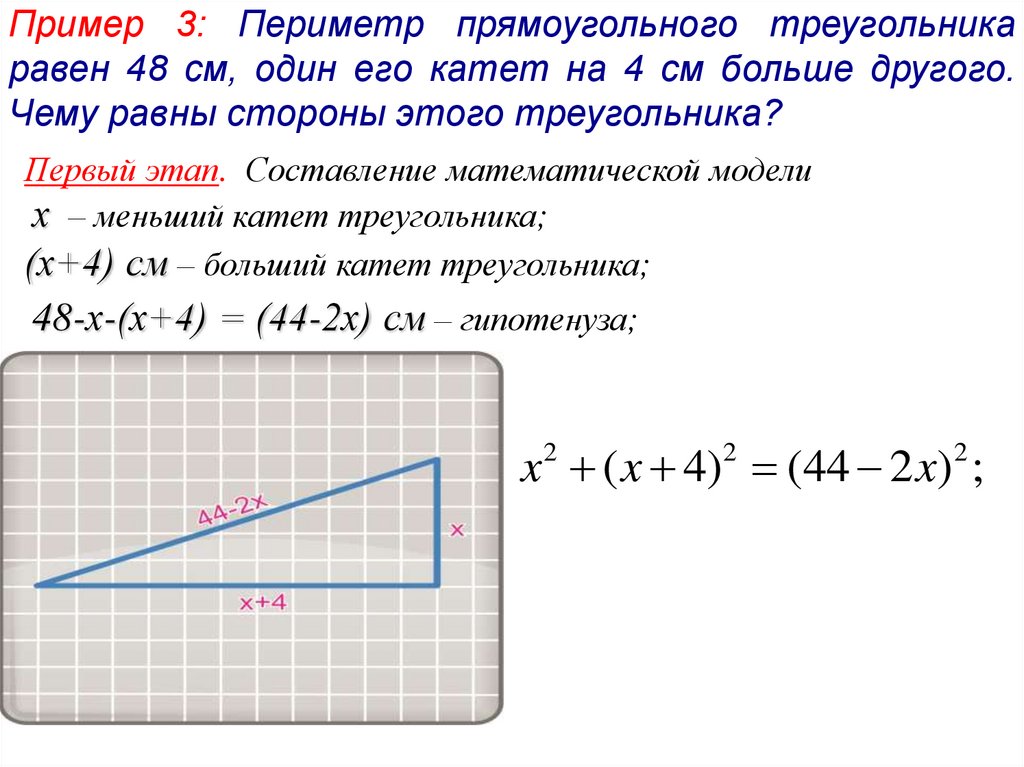
Пример 3: Периметр прямоугольного треугольника
равен 48 см, один его катет на 4 см больше другого.
Чему равны стороны этого треугольника?
Первый этап. Составление математической модели
х – меньший катет треугольника;
(х+4) см – больший катет треугольника;
48-х-(х+4) = (44-2х) см – гипотенуза;
x 2 ( x 4)2 (44 2 x)2 ;

8.

Второй этап. Работа с составленной моделью.
x 2 ( x 4)2 (44 2 x)2 ;
x 2 ( x 2 8x 16) 1936 176 x 4 x 2 ;
2 x 2 8x 16 1936 176 x 4 x 2 0;
2 x 2 184 x 1920 0;
x 2 92 x 960 0;
92 922 4 1 960 92 8464 3840 92 4624
x1,2
2
2
2
92 68
;
2
92 68
x1
80;
2
92 68
x2
12.
2

9.

Третий этап. Ответ на вопрос задачи.
х – меньший катет треугольника;
x1 80 см;
Периметр 48 см
x2 12 см;
x 12 см;
Второй катет 16 см
Гипотенуза: 48 – 12 – 16 = 20 см
12 см, 16 см, 20 см
Замечание:
х – меньший катет треугольника;
(х+4) см – больший катет треугольника;
x 2 ( x 4)2 cм
x ( x 4) x 2 ( x 4) 2 48
2 x2 8x 16 48 2 x.

10.

Пример 4: Для вывоза со склада 80 т груза автокомбинату было
заказано
некоторое
количество
машин
одинаковой
грузоподъемности. Руководство комбината решило, что на
каждую машину можно грузить на 1 т груза больше, чем
планировали на складе, и прислало на 4 машины меньше, чем
было заказано. Весь груз в итоге был вывезен. Сколько машин
было заказано и сколько прислал автокомбинат?
Первый этап. Составление математической модели
х – число машин, заказанных комбинату;
(х-4) см – число машин, которое прислал комбинат;
80
т – количество груза, которое предполагалось вывозить на
x
каждой машине;
80
т – количество груза, которое помещали на каждую
x 4
машину в действительности.
80 80
1.
x 4 x

11.

Второй этап. Работа с составленной моделью.
80 80
1;
x 4 x
х
х-4 х(х-4)
80
80
1 0;
x 4
x
80 x 80( x 4) x( x 4)
0;
x( x 4)
x 2 4 x 320
0;
x( x 4)
x 2 4 x 320 0;
x 2 4 x 320 0;
4 16 4 320 4 1296 4 36
;
x1,2
2
2
2
4 36
4 36
x1
20;
x2
16;
2
2
x( x 4) 0.

12.

Третий этап. Ответ на вопрос задачи.
х – число заказанных машин;
x 20;
Прислано машин 16
20 машин, 16 машин

13.

Пример 5: В райцентре два кинотеатра — «Факел» и «Слава»,
первый — на 400, а второй — на 600 мест. В зрительном зале
кинотеатра «Слава» на 4 ряда больше, чем в зрительном зале
кинотеатра «Факел», и, кроме того, в каждом ряду на 5 мест
больше, чем в кинотеатре «Факел». Сколько рядов в зрительном
зале кинотеатра «Факел», если известно, что в каждом ряду
кинотеатра «Слава» более 25 мест?
Первый этап. Составление математической модели
х – число рядов в кинотеатре «Факел»;
х+4 – число рядов в кинотеатре «Слава»;
400
– число мест в каждом ряду кинотеатра «Факел»;
x
600
– число мест в каждом ряду кинотеатра «Слава».
x 4
600 400
5.
x 4
x

14.

Второй этап. Работа с составленной моделью.
x1 20;
x2 16.
Третий этап. Ответ на вопрос задачи.
х – число рядов в кинотеатре «Факел»;
16 рядов